SOEM 源码解析 ecx_init_redundant
/* Initialise lib in redundant NIC mode* 在冗余网卡模式下初始化lib库* @param[in] context = context struct* 上下文结构体* @param[in] redport = pointer to redport, redundant port data* 指向冗余端口的指针,冗余端口数据* @param[in] ifname = Primary Dev name, f.e. "eth0"* 主网卡设备名称(ifname),例如“eth0”* @param[in] if2name = Secondary Dev name, f.e. "eth1"* 辅助(备用)网卡设备名称(if2name),例如“eth1”* @return >0 if OK* 如果成功,返回值>0*/
int ecx_init_redundant(ecx_contextt *context, ecx_redportt *redport, const char *ifname, char *if2name)
{int rval, /* 返回值 */zbuf;/* 临时缓冲区 */ec_etherheadert *ehp;/* 以太网报头定义 */context->port->redport /* 指向冗余端口和缓冲区的指针 */= redport;/* 指向冗余端口的指针,冗余端口数据 */ecx_setupnic(// 将 NIC 连接到套接字(socket)的基本设置。context->port,/* 端口(port) */ifname, /* 主网卡设备名称(ifname) */FALSE);/* 使用主堆栈 */rval = /* 返回值 */ecx_setupnic(// 将 NIC 连接到套接字(socket)的基本设置。context->port,/* 端口(port) */if2name,/* 辅助(备用)网卡设备名称(if2name) */TRUE);/* 使用辅助堆栈 *//* prepare "dummy" BRD tx frame for redundant operation *//* 准备“dummy”广播读(BRD) 发送帧(tx frame)以进行冗余操作 */ehp /* 以太网报头定义 */= (ec_etherheadert *)&(context->port->txbuf2);/* 临时发送缓存区 */ehp->sa1 =/* 源 MAC 地址 */oshw_htons(// 将机器上的一个无符号短整型数值(uint16)转换为网络字节序[大端模式(big - endian)]secMAC[0]);/* 用于 EtherCAT 的辅助源 MAC 地址。*/zbuf = 0;/* 临时缓冲区 *///在标准以太网帧中生成和设置 EtherCAT 数据报ecx_setupdatagram(context->port,/* 端口(port) */&(context->port->txbuf2/* 临时发送缓存区 */),// 帧缓冲区EC_CMD_BRD, /* 广播读(BRD) *//* Broadcast Read */0,/* IDX 索引 */ 0x0000,/* ADP 地址区 */0x0000,/* ADO 地址区 */2,/* 不包括 EtherCAT 报头的数据报长度 */&zbuf);/* 临时缓冲区 */context->port->txbuflength2 /* 临时发送缓存区长度 */= ETH_HEADERSIZE/* 以太网报头大小=14U */+ EC_HEADERSIZE/* EtherCAT 报头大小=12U */+ EC_WKCSIZE/* EtherCAT 数据报中工作计数器的大小=2U */+ 2;return rval;/* 返回值 */
}相关文章:

SOEM 源码解析 ecx_init_redundant
/* Initialise lib in redundant NIC mode* 在冗余网卡模式下初始化lib库* param[in] context context struct* 上下文结构体* param[in] redport pointer to redport, redundant port data* 指向冗余端口的指针ÿ…...
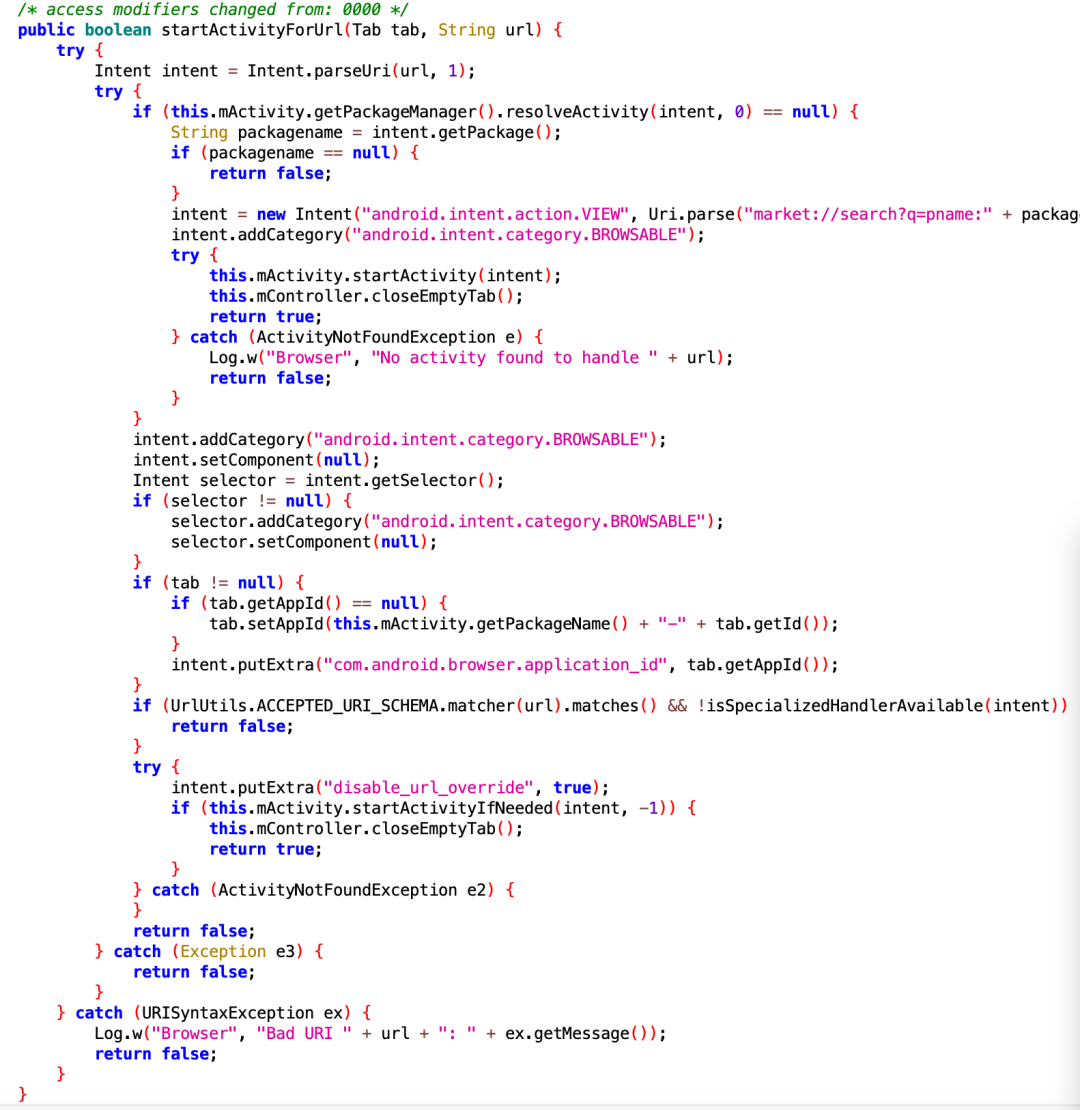
网页唤起 APP中Activity的实现原理
疑问的开端大家有没有想过一个问题:在浏览器里打开某个网页,网页上有一个按钮点击可以唤起App。这样的效果是怎么实现的呢?浏览器是一个app;为什么一个app可以调起其他app的页面?说到跨app的页面调用,大家是…...
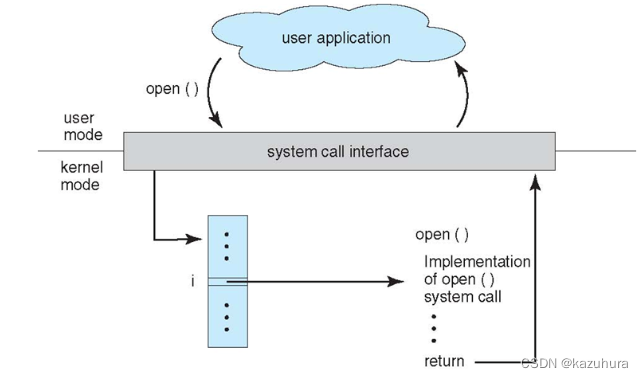
【操作系统】概述
基本特征 1. 并发 并发是指宏观上在一段时间内能同时运行多个程序,而并行则指同一时刻能运行多个指令。 并行需要硬件支持,如多流水线、多核处理器或者分布式计算系统。 操作系统通过引入进程和线程,使得程序能够并发运行 2. 共享 共享…...
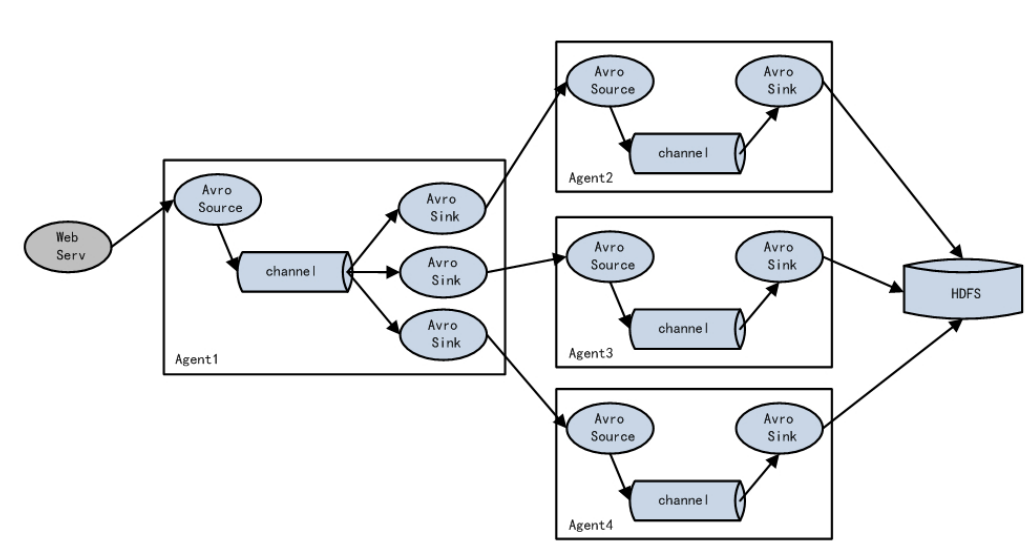
Flume三种组件的选择对比
文章目录1.source2.channel3.sink1.source Source: 数据源:通过source组件可以指定让Flume读取哪里的数据,然后将数据传递给后面的 channel Flume内置支持读取很多种数据源,基于文件、基于目录、基于TCP\UDP端口、基于HTTP、Kafka的 等等、当然了&#x…...

响应性基础API
一.什么是proxy和懒代理?什么是proxy?proxy对象是用于定义基本操作的自定义行为(如:属性查找,赋值,枚举,函数调用等等)。什么是懒代理?懒代理:在初始化的时候不会进行全部代理,而是…...

剑指 Offer 25. 合并两个排序的链表
剑指 Offer 25. 合并两个排序的链表 难度:easy\color{Green}{easy}easy 题目描述 输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。 示例1: 输入:1->2->4, 1->3->4 输出:1…...

顿悟日记(一)
目录2023年1月顿悟日记:2023年2月24日顿悟日记:2023年2月25日顿悟日记:2023年2月26日顿悟日记:顿悟的经历是如此的奇妙,且让人亢奋的事情。 2023年1月顿悟日记: 1.我是面向对象还是面向过程? …...
前端卷算法系列(二)
前端卷算法系列(二) 回文数 给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。 回文数是指正序(从左向右)和倒序(从右向左)读都是一样…...
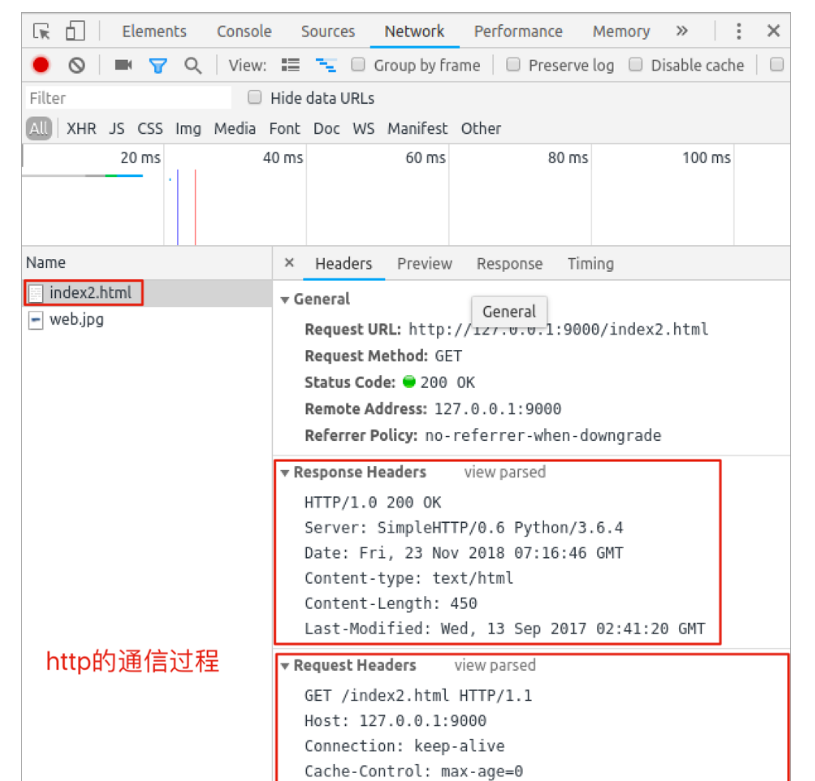
网络应用之HTTP响应报文
HTTP响应报文学习目标能够知道HTTP响应报文的结构1. HTTP响应报文分析HTTP 响应报文效果图:响应报文说明:--- 响应行/状态行 --- HTTP/1.1 200 OK # HTTP协议版本 状态码 状态描述 --- 响应头 --- Server: Tengine # 服务器名称 Content-Type: text/html; charsetUTF-8 # 内容类…...

常见的CSS技巧
1.禁止长按图片弹出菜单 img {-webkit-touch-callout: none; // 主要用于禁止长按菜单。主针对webkit内核的浏览器; } /*或者 user-select , 是css3的新属性,用于设置用户是否能够选中文本*/ .img {-webkit-user-select: none;-khtml-user-select: none…...
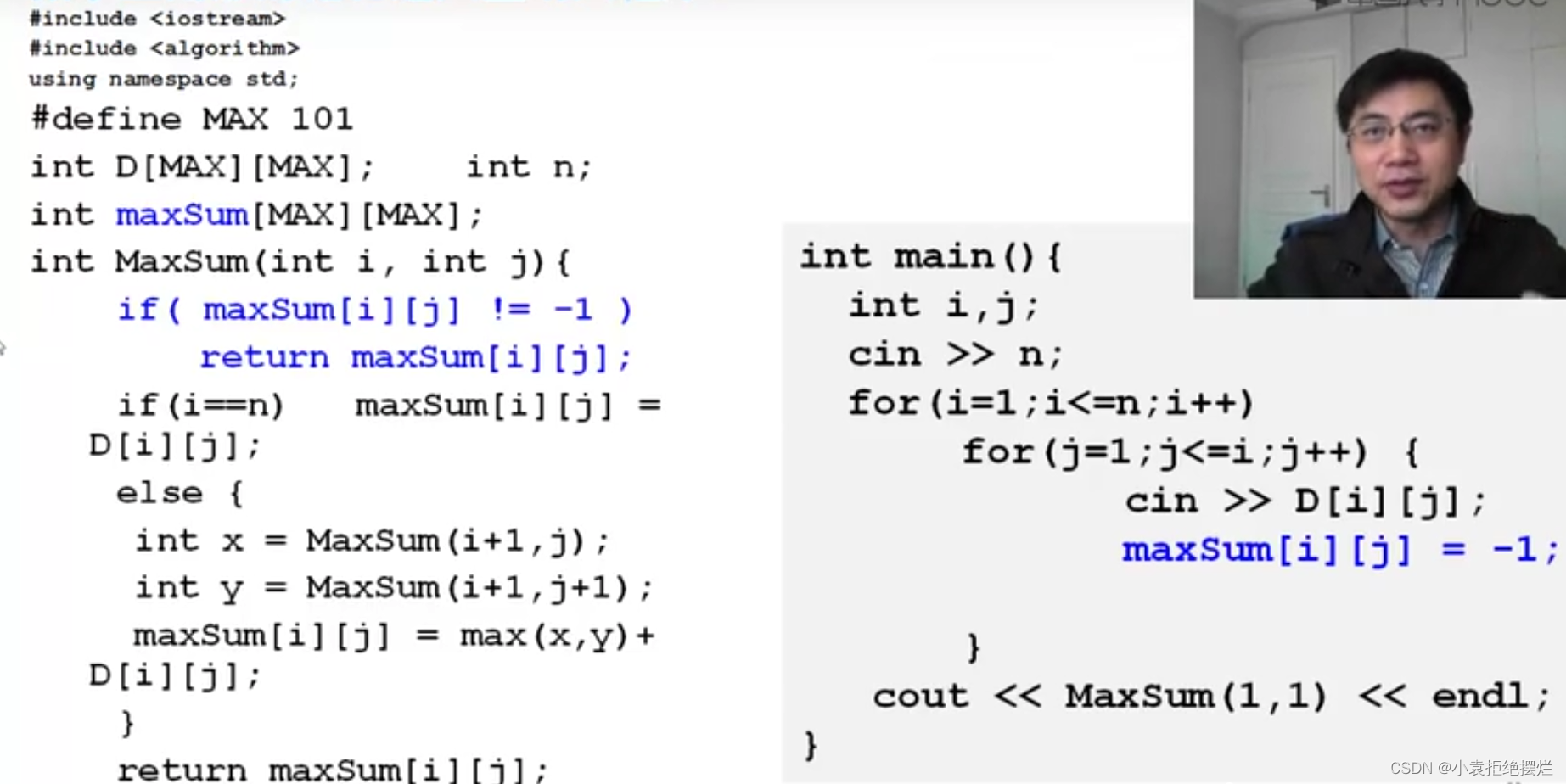
算法进阶-动态规划
经典例题 大家肯定想用递归做 思路大概就是这样 递归到最后一行就是对应的D(i,j) 然后往上推 但是这样会超时,因为存在大量的重复计算 比如调用第一行MasSum(7)需要调用MaxSum(3)和MaxSum(8) 但是调用第二行MaxSum(3)还要调用3行的MaxSum(8)和3行的MaxSum(1) 第二行…...

python的读写操作
一、使用open函数,可以打开一个已经存在的文件,或着创建一个新文件 语法如下: open(name, mode, encoding) name: 要打开的目标文件的字符串(可以包含文件所在的具体路径) mode: 打开文件模式:只读(r)、写入(w)、追加(a)等 e…...
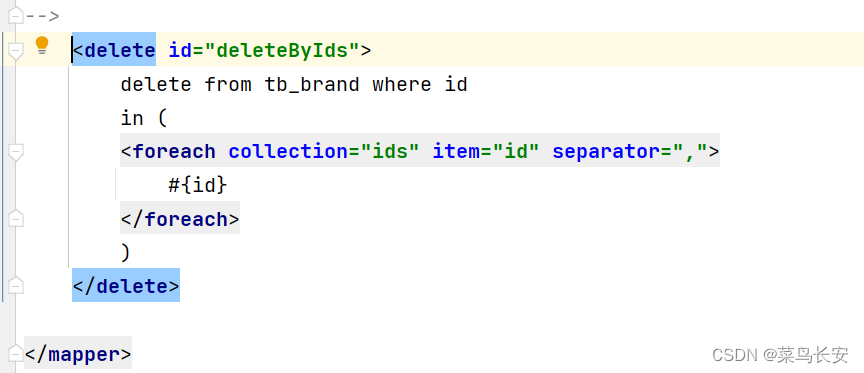
Mybatis中添加、查询、修改、删除
在Mybatis中添加数据的操作 编写相对应的SQL语句,并完成相关数据的对应关系 编写测试用例 需要提交事务 sqlSession commit() 这里需要注意的是mybatis是默认的是手动提交事务,如果不写的话会进行回滚,添加操作就不会被执行 或者在 如果…...
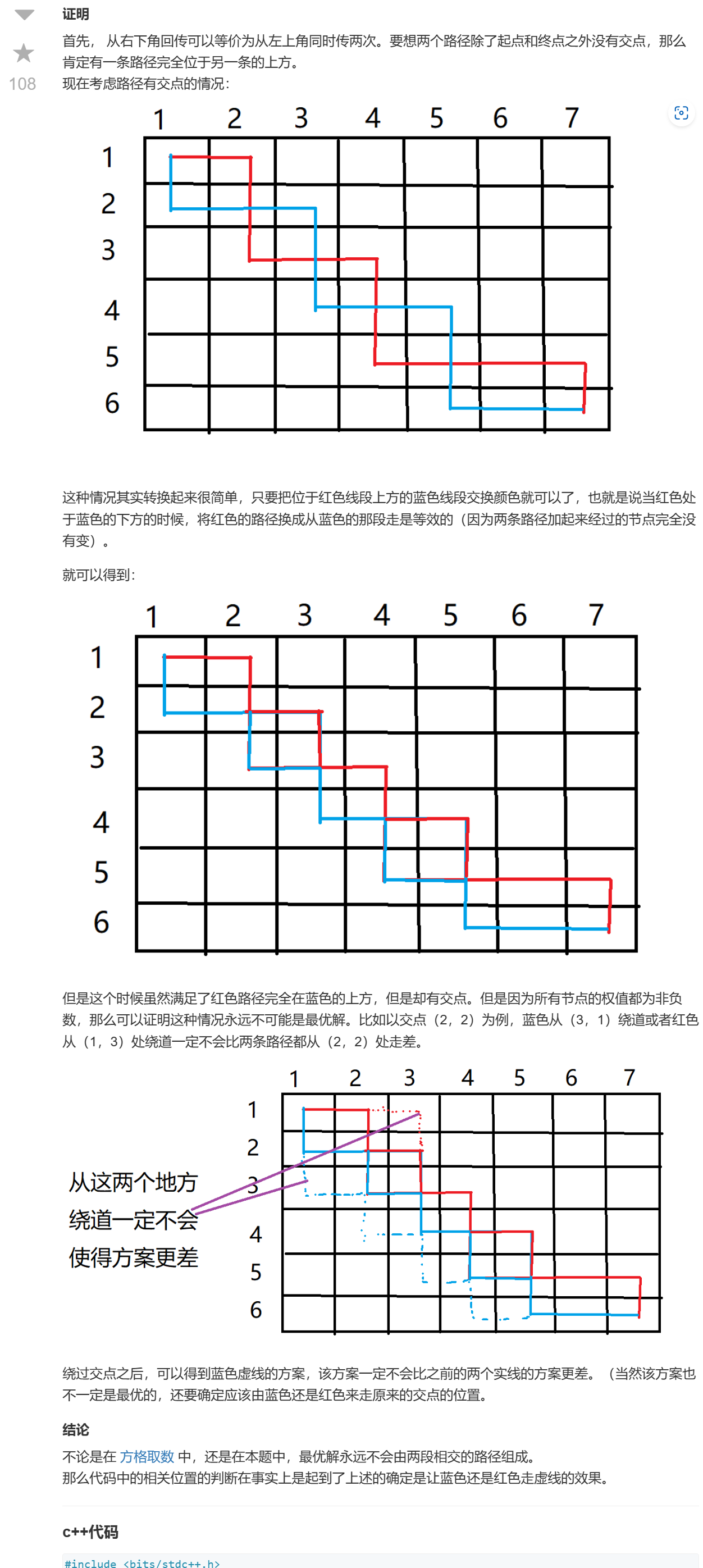
C++---线性dp---传纸条(每日一道算法2023.2.26)
注意事项: 本题dp思路与 “线性dp–方格取数” 一致,下方思路仅证明为什么使用方格取数的思路是正确的。 题目: 小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。 一次素质拓展活动中,班上同学安排坐成…...

浅谈 C/C++ 的输入输出
更好的阅读体验\huge{\color{red}{更好的阅读体验}}更好的阅读体验 文章目录0. 叠甲,过1. 谈谈输入输出缓冲区1.1 基本概念输入输出流标准输入输出流文件输入输出流1.2 输入输出缓冲区什么是输入输出缓冲区?为什么要设置输入输出缓冲区?C/C 的…...
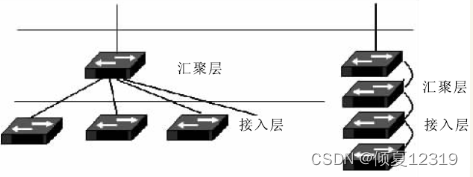
【计算机三级网络技术】 第二篇 中小型系统总体规划与设计
文章目录一、基于网络的信息系统基本结构二、划分网络系统组建工程阶段三、网络需求调研与系统设计原则四、网络用户调查与网络工程需求分析1.网络用户调查2.网络节点的地理位置分布3.应用概要分析4.网络需求详细分析五、网络总体设计基本方法1.网络工程建设总体目标与设计原则…...
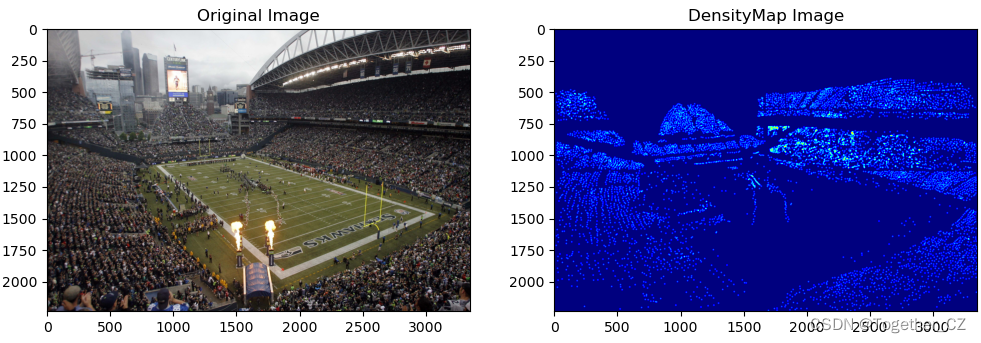
Boosting Crowd Counting via Multifaceted Attention之人群密度估计实践
这周闲来无事,看到一篇前不久刚发表的文章,是做密集人群密度估计的,这块我之前虽然也做过,但是主要是基于检测的方式实现的,这里提出来的方法还是比较有意思的,就拿来实践一下。论文在这里,感兴…...
python之面向对象编程
1、面向对象介绍: 世界万物,皆可分类 世界万物,皆为对象 只要是对象,就肯定属于某种类 只要是对象,就肯定有属性 2、 面向对象的几个特性: class类: 一个类即对一类拥有相同属性的对象的…...
(七))
常见前端基础面试题(HTML,CSS,JS)(七)
同源策略 浏览器有一个重要的安全策略,称之为同源策略 其中,协议、端口号、域名必须一致,,称之为同源,两个源不同,称之为跨源或跨域 同源策略是指,若页面的源和页面运行过程中加载的源不一致…...

产业链金风控基本逻辑
产业链金风控基本逻辑 产业链金融平台作为一个助贷平台,很大程度上是为银行等金融机构进 行引流,贷款的审批本质上还是依赖金融机构的风控。那么,产业链金融 平台是否还有必要建设自己的风控模型呢?笔者给出的答案是肯定的。 一方面&#x…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
