【改进灰狼优化算法】改进收敛因子和比例权重的灰狼优化算法【期刊论文完美复现】(Matlab代码实现)
👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 文献来源
🌈4 Matlab代码实现
💥1 概述
文献来源:

摘要:在分析灰狼优化算法不足的基础上,提出一种改进的灰狼优化算法(CGWO),该算法采用基于余弦规律变化的收敛因子,平衡算法的全局搜索和局部搜索能力,同时引入基于步长欧氏距离的比例权重更新灰狼位置,从而加快算法的收敛速度。对8个经典测试函数进行仿真实验,结果表明CGWO算法的求解精度更高,稳定性更好。最后以预测谷氨酸菌体生长浓度为例,利用CGWO算法估计Richards模型的参数,以均方根误差和平均绝对误差作为评价指标,与PSO算法、GA算法和VS-FOA算法的结果进行比较,CGWO算法可以有效地估计Richards模型中的参数。
关键词:
灰狼优化算法;收敛因子;Richards模型;参数估计;
📚2 运行结果


部分代码:
function [Alpha_score,Alpha_pos,Convergence_curve]=CGWO(SearchAgents_no,Max_iter,lb,ub,dim,fobj)
%% 收敛因子参数
aintit = 2;
afinal = 0;
% initialize alpha, beta, and delta_pos
Alpha_pos=zeros(1,dim);
Alpha_score=inf; %change this to -inf for maximization problems
Beta_pos=zeros(1,dim);
Beta_score=inf; %change this to -inf for maximization problems
Delta_pos=zeros(1,dim);
Delta_score=inf; %change this to -inf for maximization problems
%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);
Convergence_curve=zeros(1,Max_iter);
l=0;% Loop counter
% Main loop
while l<Max_iter
for i=1:size(Positions,1)
% Return back the search agents that go beyond the boundaries of the search space
Flag4ub=Positions(i,:)>ub;
Flag4lb=Positions(i,:)<lb;
Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
% Calculate objective function for each search agent
fitness=fobj(Positions(i,:));
% Update Alpha, Beta, and Delta
if fitness<Alpha_score
Alpha_score=fitness; % Update alpha
Alpha_pos=Positions(i,:);
end
if fitness>Alpha_score && fitness<Beta_score
Beta_score=fitness; % Update beta
Beta_pos=Positions(i,:);
end
if fitness>Alpha_score && fitness>Beta_score && fitness<Delta_score
Delta_score=fitness; % Update delta
Delta_pos=Positions(i,:);
end
end
%% 改进点:收敛因子改进,文献中式(7)
n = 1;%递减系数
if(l<0.5*Max_iter)
a = afinal + (aintit - afinal)*(1 + (cos((l-1)*pi/( Max_iter-1)))^n)/2;
else
a = afinal + (aintit - afinal)*(1 - (cos((l-1)*pi/( Max_iter-1)))^n)/2;
end
% Update the Position of search agents including omegas
for i=1:size(Positions,1)
for j=1:size(Positions,2)
r1=rand(); % r1 is a random number in [0,1]
r2=rand(); % r2 is a random number in [0,1]
A1=2*a*r1-a; % Equation (3.3)
C1=2*r2; % Equation (3.4)
D_alpha=abs(C1*Alpha_pos(j)-Positions(i,j)); % Equation (3.5)-part 1
X1=Alpha_pos(j)-A1*D_alpha; % Equation (3.6)-part 1
r1=rand();
r2=rand();
A2=2*a*r1-a; % Equation (3.3)
C2=2*r2; % Equation (3.4)
D_beta=abs(C2*Beta_pos(j)-Positions(i,j)); % Equation (3.5)-part 2
X2=Beta_pos(j)-A2*D_beta; % Equation (3.6)-part 2
r1=rand();
r2=rand();
A3=2*a*r1-a; % Equation (3.3)
C3=2*r2; % Equation (3.4)
D_delta=abs(C3*Delta_pos(j)-Positions(i,j)); % Equation (3.5)-part 3
X3=Delta_pos(j)-A3*D_delta; % Equation (3.5)-part 3
%% 改进点:基于步长欧氏距离的比例权重
S = abs(X1) + abs(X2)+abs(X3);
if S~=0 %防止分母为0
W1 = abs(X1)/(abs(X1) + abs(X2)+abs(X3));
W2 = abs(X2)/(abs(X1) + abs(X2)+abs(X3));
W3 = abs(X3)/(abs(X1) + abs(X2)+abs(X3));
else
W1=1;W2=1;W3=1;
end
Positions(i,j)=(W1*X1+X2*W2+X3*W3)/3;% Equation (3.7)
end
end
l=l+1;
Convergence_curve(l)=Alpha_score;
end
🎉3 文献来源
部分理论来源于网络,如有侵权请联系删除。
[1]王秋萍,王梦娜,王晓峰.改进收敛因子和比例权重的灰狼优化算法[J].计算机工程与应用,2019,55(21):60-65+98.
🌈4 Matlab代码实现
相关文章:

【改进灰狼优化算法】改进收敛因子和比例权重的灰狼优化算法【期刊论文完美复现】(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

Linux C代码获取线程ID
Linux C代码获取线程ID gettid可以获取线程id,但是通过man gettid可以看到下面这两句 也就是说glibc没有为这个gettid封装系统调用,需要使用syscall。 #define _GNU_SOURCE#include <unistd.h>#include <sys/syscall.h>#include <sys/types.h>pi…...
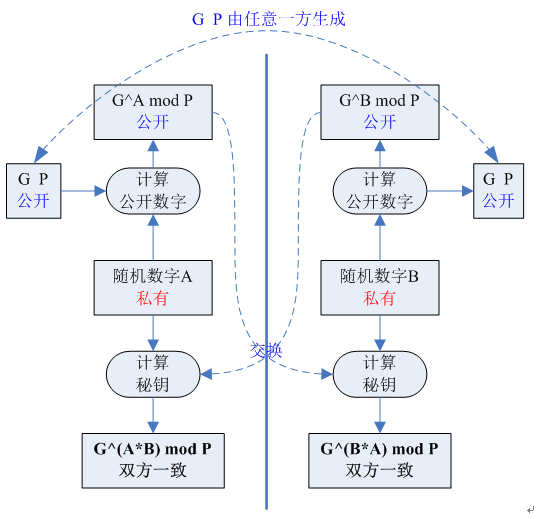
基本密码技术
AESAES取代DES,是一种对称加密技术,分为AES-128/192/256, 其分组长度固定为128b,若最后一个分组长度不够,需要补全至128b长度。所支持的秘钥长度分别为128b/192b/256b.分组密码模式AES是对明文进行分组之后逐块进行加密࿰…...
【力扣周赛#334】6369. 左右元素和的差值 + 6368. 找出字符串的可整除数组 + 6367. 求出最多标记下标
目录 6369. 左右元素和的差值 - 前缀后缀和 ac 6368. 找出字符串的可整除数组 - 操作余数ac 6367. 求出最多标记下标 - 二分答案 贪心 6369. 左右元素和的差值 - 前缀后缀和 ac class Solution {public int[] leftRigthDifference(int[] nums) {int nnums.length;int[] re…...
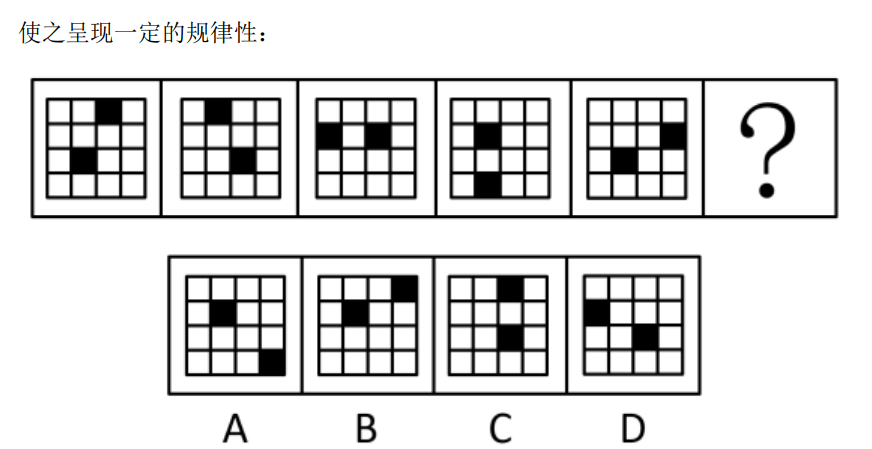
行测-判断推理-图形推理-位置规律-平移
位置平移,选D空白每次顺时针移动一格,黑色圆每次逆时针移动2格选C两个黑色⚪,每次顺时针移动2格白色⚪,先到对角位置,再顺时针移动一格选B三角形的底,顺时针移动三角形的顶点,在正方形的内部顺时…...
)
数据库基础知识(一)
目录 什么是数据库 表,列,行 主键 什么是SQL 什么是数据库 数据库(database):保存有组织的数据的容器(通常是一个文件或一组文件)。 数据库软件(DMBS):又名数据库管理系统。数据库是通过数据库软件创建和操纵的容器。因为你并…...
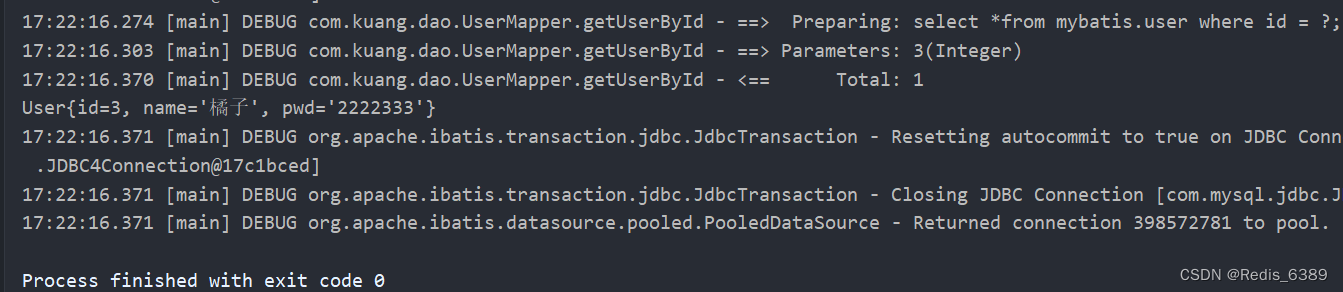
MyBatis 的工作原理解析
文章目录前言一、mybatis工作原理1.1 流程图1.2 步骤解析1.3 代码实现前言 本文记录 Mybatis 的工作原理,做到知识梳理总结的作用。 一、mybatis工作原理 Mybatis 的总体工作原理流程图如下图所示 1.1 流程图 1.2 步骤解析 Mybatis 框架在工作时大致经过8个步骤…...
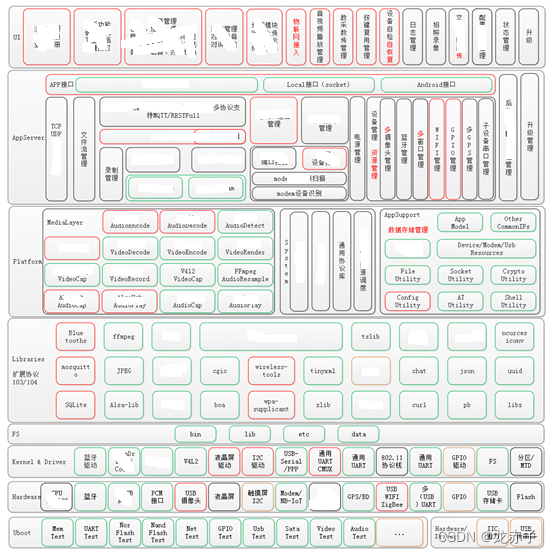
终端软件架构说
目录 零:前言 一,基于服务的架构 二,基于多进程多线程的架构 三,以数据为中心的架构 四,类Android的分层架构设计 五,总结 零:前言 谈到架构,可能大家的第一感觉是信息系统的…...

LearnOpenGL-入门-你好,三角形
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject LearnOpenGL中文官网:https://learnopengl-cn.github.io/ 文章目录图形渲染管线基本介绍着色器…...

SOEM 源码解析 ecx_init_redundant
/* Initialise lib in redundant NIC mode* 在冗余网卡模式下初始化lib库* param[in] context context struct* 上下文结构体* param[in] redport pointer to redport, redundant port data* 指向冗余端口的指针ÿ…...
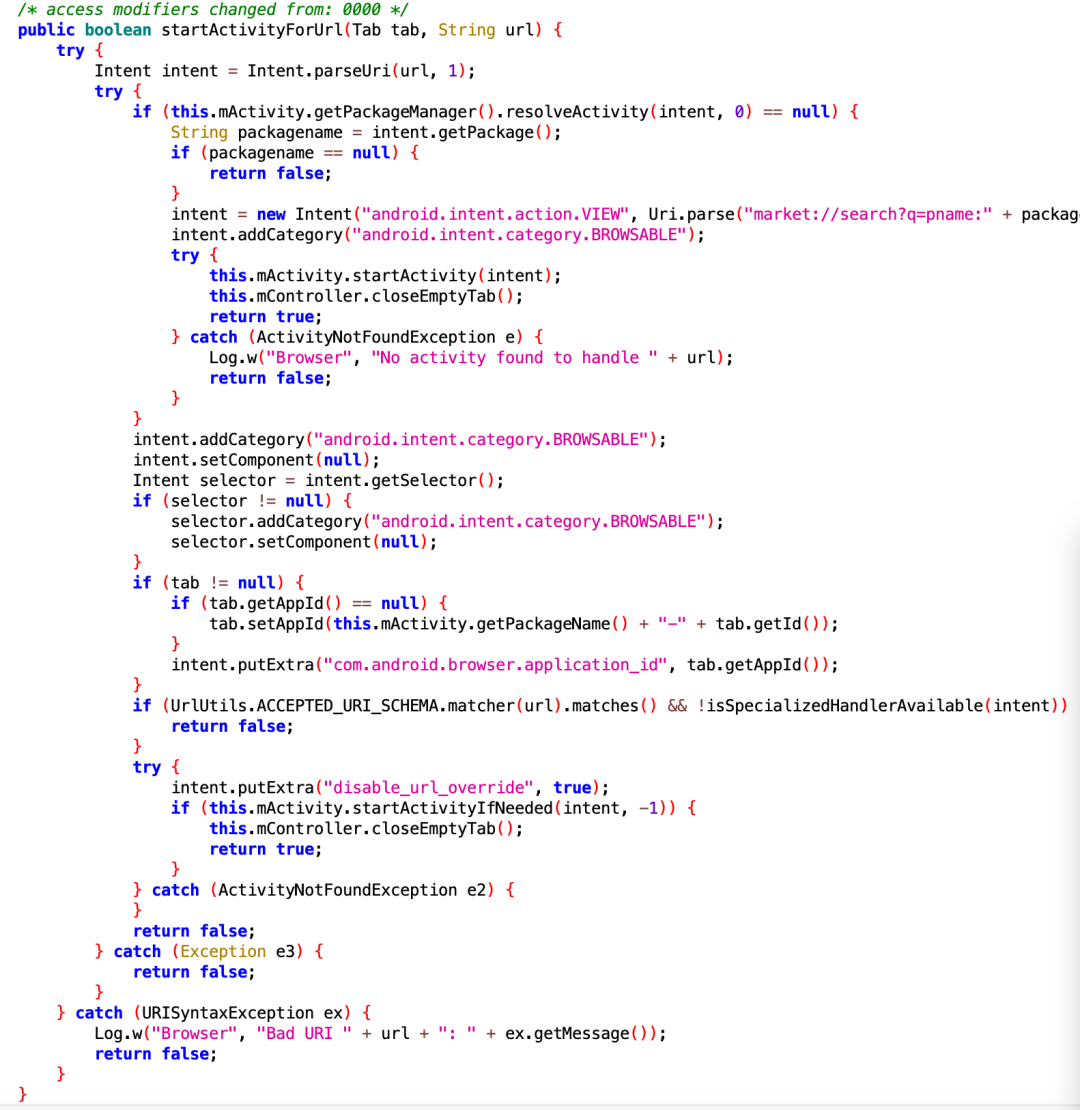
网页唤起 APP中Activity的实现原理
疑问的开端大家有没有想过一个问题:在浏览器里打开某个网页,网页上有一个按钮点击可以唤起App。这样的效果是怎么实现的呢?浏览器是一个app;为什么一个app可以调起其他app的页面?说到跨app的页面调用,大家是…...
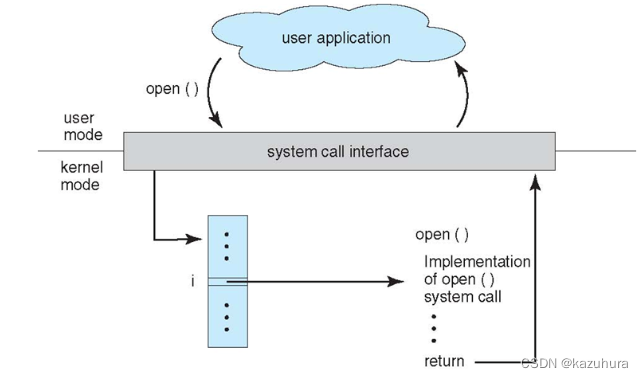
【操作系统】概述
基本特征 1. 并发 并发是指宏观上在一段时间内能同时运行多个程序,而并行则指同一时刻能运行多个指令。 并行需要硬件支持,如多流水线、多核处理器或者分布式计算系统。 操作系统通过引入进程和线程,使得程序能够并发运行 2. 共享 共享…...
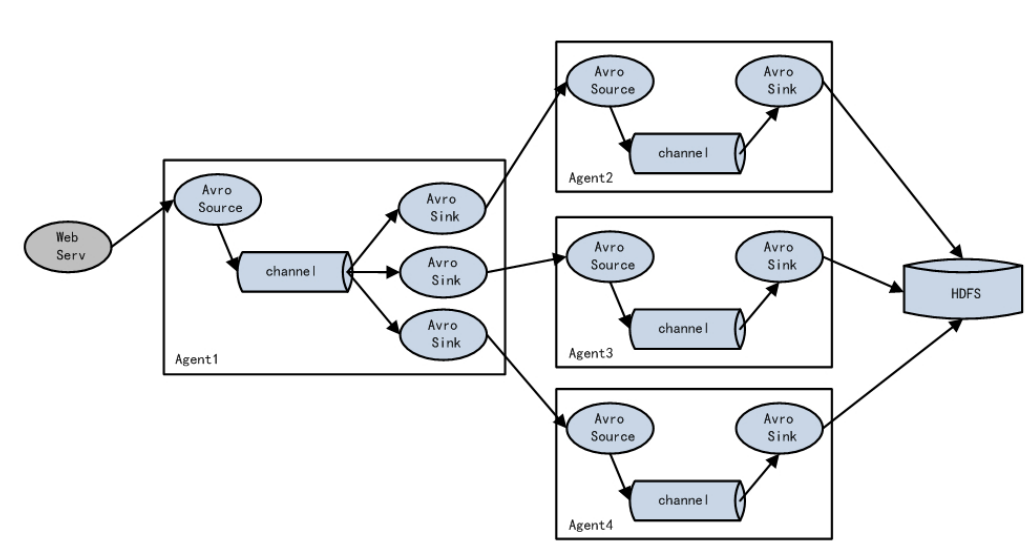
Flume三种组件的选择对比
文章目录1.source2.channel3.sink1.source Source: 数据源:通过source组件可以指定让Flume读取哪里的数据,然后将数据传递给后面的 channel Flume内置支持读取很多种数据源,基于文件、基于目录、基于TCP\UDP端口、基于HTTP、Kafka的 等等、当然了&#x…...

响应性基础API
一.什么是proxy和懒代理?什么是proxy?proxy对象是用于定义基本操作的自定义行为(如:属性查找,赋值,枚举,函数调用等等)。什么是懒代理?懒代理:在初始化的时候不会进行全部代理,而是…...

剑指 Offer 25. 合并两个排序的链表
剑指 Offer 25. 合并两个排序的链表 难度:easy\color{Green}{easy}easy 题目描述 输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。 示例1: 输入:1->2->4, 1->3->4 输出:1…...

顿悟日记(一)
目录2023年1月顿悟日记:2023年2月24日顿悟日记:2023年2月25日顿悟日记:2023年2月26日顿悟日记:顿悟的经历是如此的奇妙,且让人亢奋的事情。 2023年1月顿悟日记: 1.我是面向对象还是面向过程? …...
前端卷算法系列(二)
前端卷算法系列(二) 回文数 给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。 回文数是指正序(从左向右)和倒序(从右向左)读都是一样…...
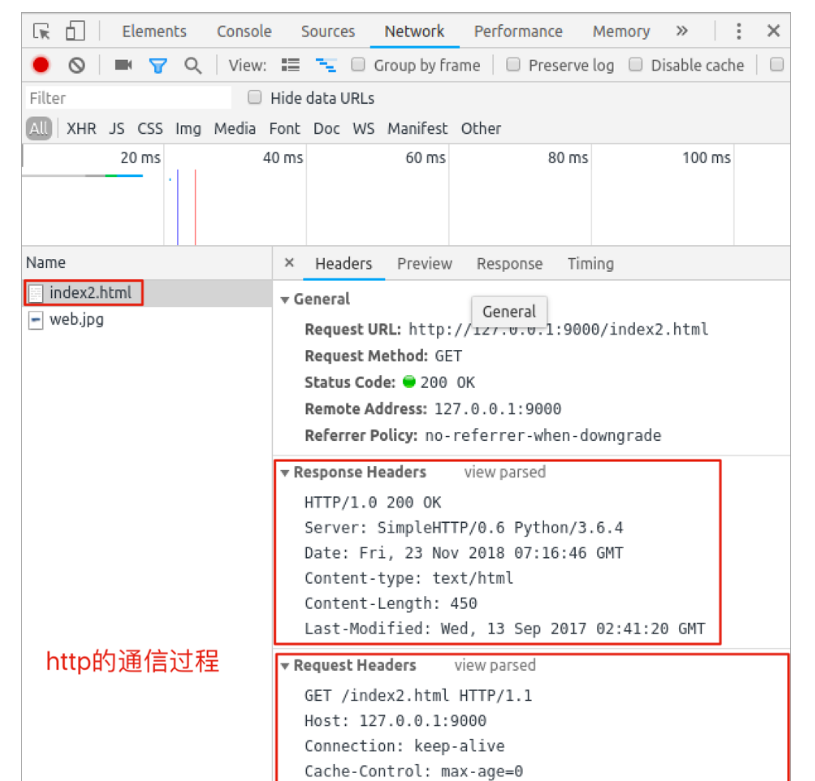
网络应用之HTTP响应报文
HTTP响应报文学习目标能够知道HTTP响应报文的结构1. HTTP响应报文分析HTTP 响应报文效果图:响应报文说明:--- 响应行/状态行 --- HTTP/1.1 200 OK # HTTP协议版本 状态码 状态描述 --- 响应头 --- Server: Tengine # 服务器名称 Content-Type: text/html; charsetUTF-8 # 内容类…...

常见的CSS技巧
1.禁止长按图片弹出菜单 img {-webkit-touch-callout: none; // 主要用于禁止长按菜单。主针对webkit内核的浏览器; } /*或者 user-select , 是css3的新属性,用于设置用户是否能够选中文本*/ .img {-webkit-user-select: none;-khtml-user-select: none…...
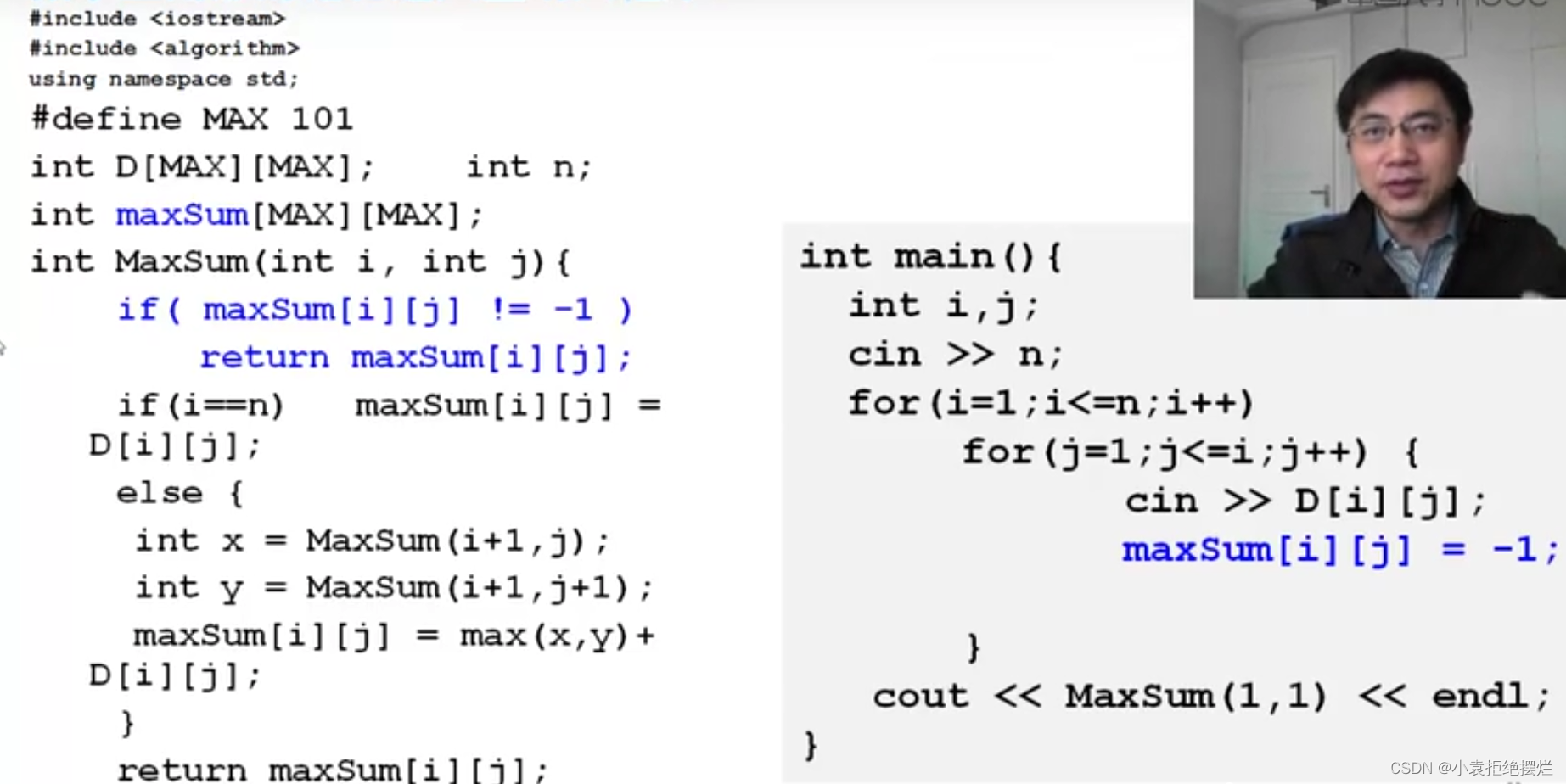
算法进阶-动态规划
经典例题 大家肯定想用递归做 思路大概就是这样 递归到最后一行就是对应的D(i,j) 然后往上推 但是这样会超时,因为存在大量的重复计算 比如调用第一行MasSum(7)需要调用MaxSum(3)和MaxSum(8) 但是调用第二行MaxSum(3)还要调用3行的MaxSum(8)和3行的MaxSum(1) 第二行…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
