角度制与弧度制的相互转换np.deg2radnp.rad2deg
【小白从小学Python、C、Java】
【计算机等级考试+500强双证书】
【Python-数据分析】
角度制与弧度制的相互转换
np.deg2rad
np.rad2deg
选择题
以下关于python代码表述错误的一项是?
import numpy as np
print("【执行】np.rad2deg(np.pi)")
print(np.rad2deg(np.pi))
print("【执行】np.deg2rad(180)")
print(np.deg2rad(180))
A选项:deg2rad将弧度制转为角度制
B选项:Π转换为角度制结果是180°
C选项:np.pi是圆周率的值
D选项:弧度制与角度制可以相互转换
答案:A
问题解析:

程序及执行结果:

温馨期待
期待大家提出宝贵建议,互相交流,收获更大,助教:hzy
#IT研究所# [握手] #30天快速上手python数据分析#
欢迎大家转发,一起传播知识和正能量,帮助到更多人。期待大家提出宝贵改进建议,互相交流,收获更大。辛苦大家转发时注明出处(也是咱们公益编程交流群的入口网址),刘经纬老师共享知识相关文件下载地址为:https://liujingwei.cn
相关文章:

角度制与弧度制的相互转换np.deg2radnp.rad2deg
【小白从小学Python、C、Java】【计算机等级考试500强双证书】【Python-数据分析】角度制与弧度制的相互转换np.deg2radnp.rad2deg选择题以下关于python代码表述错误的一项是?import numpy as npprint("【执行】np.rad2deg(np.pi)")print(np.rad2deg(np.pi))print(&…...
)
【SAP Abap】X-DOC:SAP ABAP 语法更新之一(Open SQL新增特性)
SAP ABAP 语法更新之一(Open SQL新增特性)1、前言2、演示1、前言 自从 SAP 推出 SAP ON HANA,与之相随的 AS ABAP NW 7.40 版本以后,ABAP 语法也有了较多的更新,本篇对 Open Sql的语法更新部分做一个DEMO演示。 NW 7…...

【改进灰狼优化算法】改进收敛因子和比例权重的灰狼优化算法【期刊论文完美复现】(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

Linux C代码获取线程ID
Linux C代码获取线程ID gettid可以获取线程id,但是通过man gettid可以看到下面这两句 也就是说glibc没有为这个gettid封装系统调用,需要使用syscall。 #define _GNU_SOURCE#include <unistd.h>#include <sys/syscall.h>#include <sys/types.h>pi…...
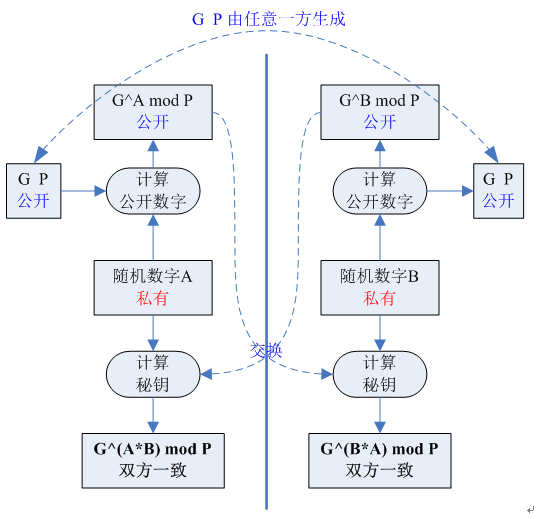
基本密码技术
AESAES取代DES,是一种对称加密技术,分为AES-128/192/256, 其分组长度固定为128b,若最后一个分组长度不够,需要补全至128b长度。所支持的秘钥长度分别为128b/192b/256b.分组密码模式AES是对明文进行分组之后逐块进行加密࿰…...
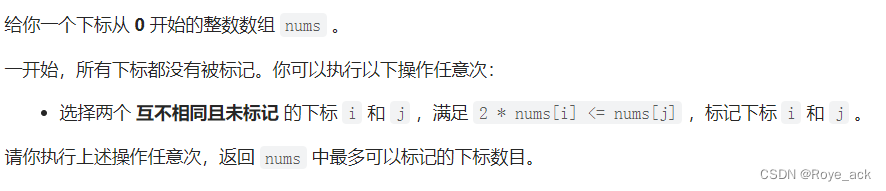
【力扣周赛#334】6369. 左右元素和的差值 + 6368. 找出字符串的可整除数组 + 6367. 求出最多标记下标
目录 6369. 左右元素和的差值 - 前缀后缀和 ac 6368. 找出字符串的可整除数组 - 操作余数ac 6367. 求出最多标记下标 - 二分答案 贪心 6369. 左右元素和的差值 - 前缀后缀和 ac class Solution {public int[] leftRigthDifference(int[] nums) {int nnums.length;int[] re…...
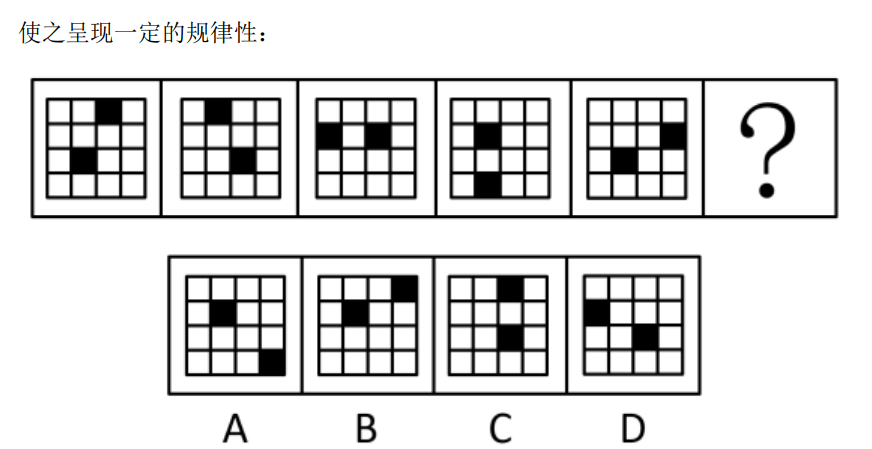
行测-判断推理-图形推理-位置规律-平移
位置平移,选D空白每次顺时针移动一格,黑色圆每次逆时针移动2格选C两个黑色⚪,每次顺时针移动2格白色⚪,先到对角位置,再顺时针移动一格选B三角形的底,顺时针移动三角形的顶点,在正方形的内部顺时…...
)
数据库基础知识(一)
目录 什么是数据库 表,列,行 主键 什么是SQL 什么是数据库 数据库(database):保存有组织的数据的容器(通常是一个文件或一组文件)。 数据库软件(DMBS):又名数据库管理系统。数据库是通过数据库软件创建和操纵的容器。因为你并…...
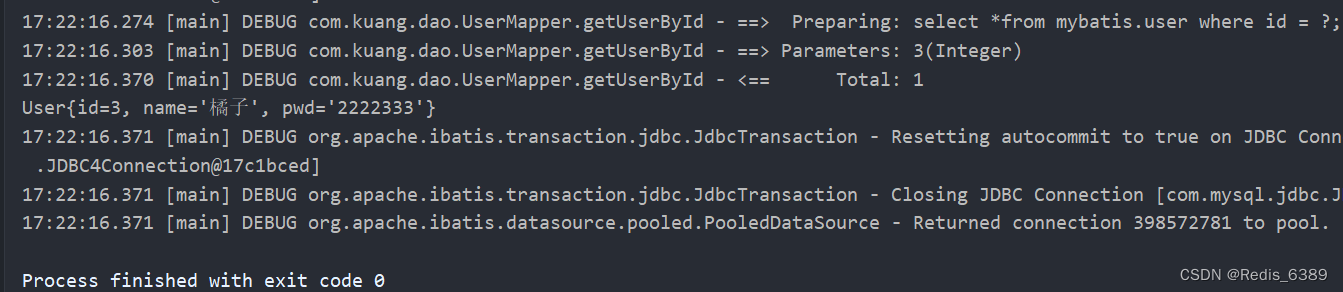
MyBatis 的工作原理解析
文章目录前言一、mybatis工作原理1.1 流程图1.2 步骤解析1.3 代码实现前言 本文记录 Mybatis 的工作原理,做到知识梳理总结的作用。 一、mybatis工作原理 Mybatis 的总体工作原理流程图如下图所示 1.1 流程图 1.2 步骤解析 Mybatis 框架在工作时大致经过8个步骤…...
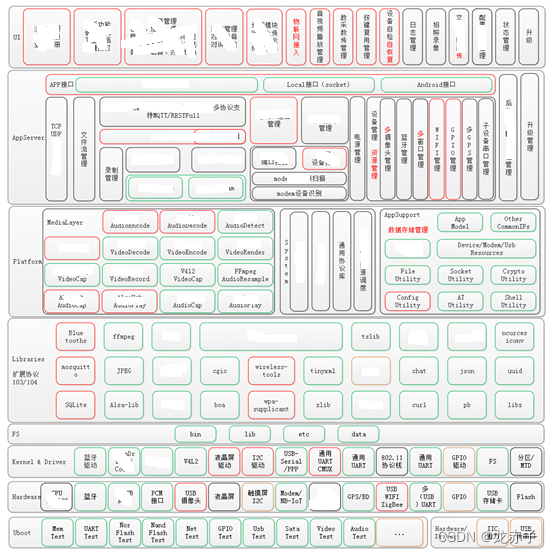
终端软件架构说
目录 零:前言 一,基于服务的架构 二,基于多进程多线程的架构 三,以数据为中心的架构 四,类Android的分层架构设计 五,总结 零:前言 谈到架构,可能大家的第一感觉是信息系统的…...

LearnOpenGL-入门-你好,三角形
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject LearnOpenGL中文官网:https://learnopengl-cn.github.io/ 文章目录图形渲染管线基本介绍着色器…...

SOEM 源码解析 ecx_init_redundant
/* Initialise lib in redundant NIC mode* 在冗余网卡模式下初始化lib库* param[in] context context struct* 上下文结构体* param[in] redport pointer to redport, redundant port data* 指向冗余端口的指针ÿ…...
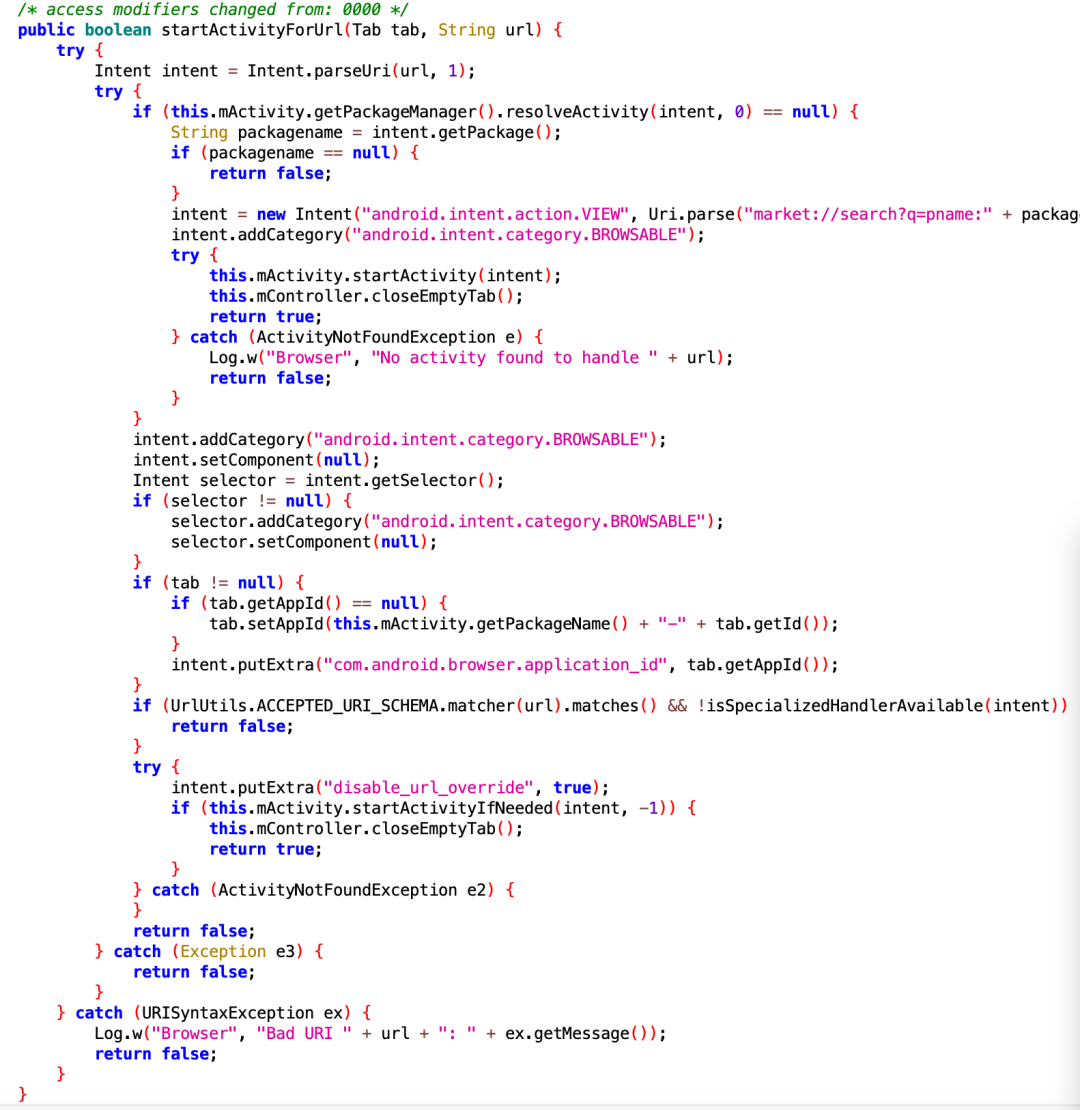
网页唤起 APP中Activity的实现原理
疑问的开端大家有没有想过一个问题:在浏览器里打开某个网页,网页上有一个按钮点击可以唤起App。这样的效果是怎么实现的呢?浏览器是一个app;为什么一个app可以调起其他app的页面?说到跨app的页面调用,大家是…...
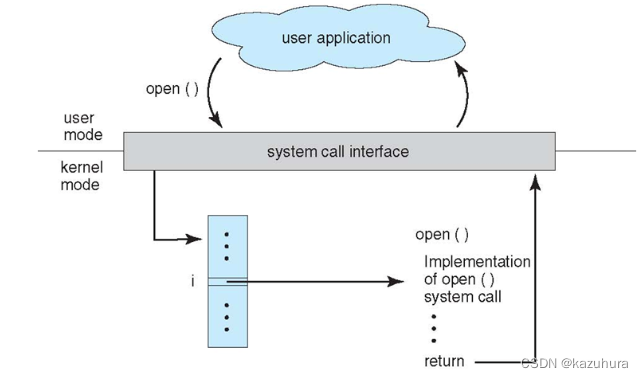
【操作系统】概述
基本特征 1. 并发 并发是指宏观上在一段时间内能同时运行多个程序,而并行则指同一时刻能运行多个指令。 并行需要硬件支持,如多流水线、多核处理器或者分布式计算系统。 操作系统通过引入进程和线程,使得程序能够并发运行 2. 共享 共享…...
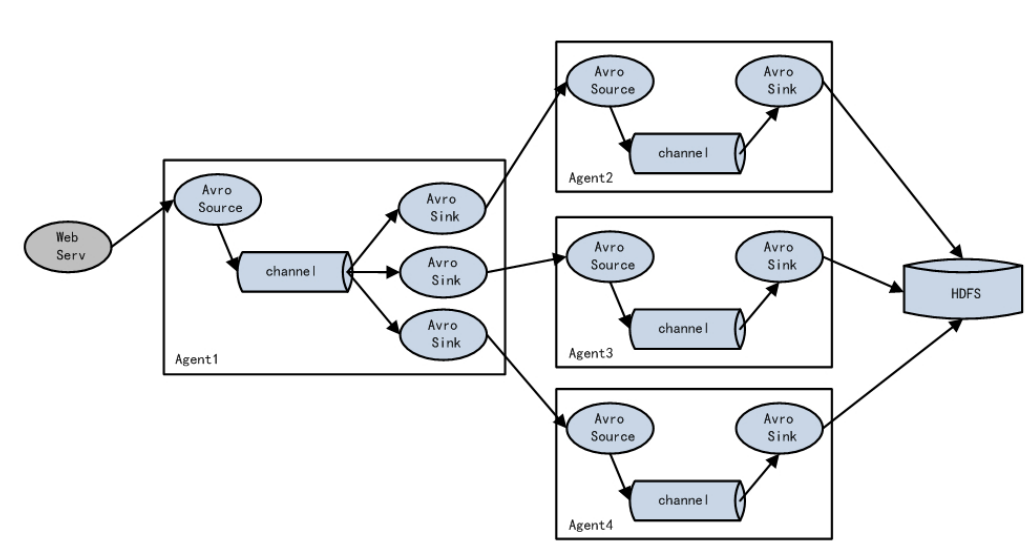
Flume三种组件的选择对比
文章目录1.source2.channel3.sink1.source Source: 数据源:通过source组件可以指定让Flume读取哪里的数据,然后将数据传递给后面的 channel Flume内置支持读取很多种数据源,基于文件、基于目录、基于TCP\UDP端口、基于HTTP、Kafka的 等等、当然了&#x…...

响应性基础API
一.什么是proxy和懒代理?什么是proxy?proxy对象是用于定义基本操作的自定义行为(如:属性查找,赋值,枚举,函数调用等等)。什么是懒代理?懒代理:在初始化的时候不会进行全部代理,而是…...

剑指 Offer 25. 合并两个排序的链表
剑指 Offer 25. 合并两个排序的链表 难度:easy\color{Green}{easy}easy 题目描述 输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。 示例1: 输入:1->2->4, 1->3->4 输出:1…...

顿悟日记(一)
目录2023年1月顿悟日记:2023年2月24日顿悟日记:2023年2月25日顿悟日记:2023年2月26日顿悟日记:顿悟的经历是如此的奇妙,且让人亢奋的事情。 2023年1月顿悟日记: 1.我是面向对象还是面向过程? …...
前端卷算法系列(二)
前端卷算法系列(二) 回文数 给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。 回文数是指正序(从左向右)和倒序(从右向左)读都是一样…...
网络应用之HTTP响应报文
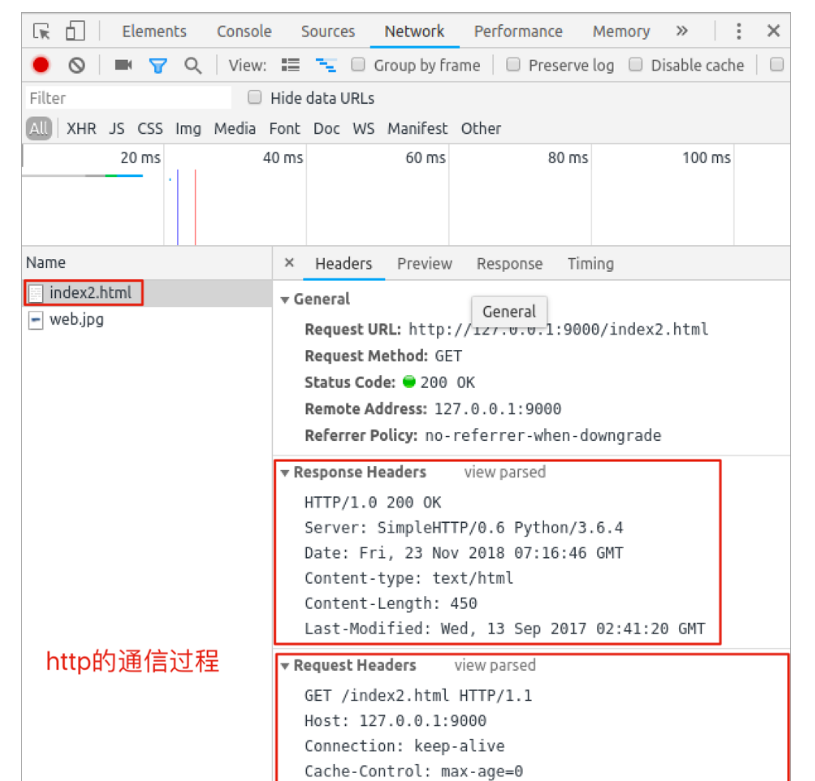
HTTP响应报文学习目标能够知道HTTP响应报文的结构1. HTTP响应报文分析HTTP 响应报文效果图:响应报文说明:--- 响应行/状态行 --- HTTP/1.1 200 OK # HTTP协议版本 状态码 状态描述 --- 响应头 --- Server: Tengine # 服务器名称 Content-Type: text/html; charsetUTF-8 # 内容类…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...
