11、电路综合-集总参数电路结构的S参数模型计算与Matlab
11、电路综合-集总参数电路结构的S参数模型
电路综合专栏的大纲如下:
网络综合和简化实频理论学习概述
前面介绍了许多微带线电路综合的实际案例,如:
3、电路综合原理与实践—单双端口理想微带线(伪)手算S参数与时域波形
介绍了微带线电路的频域与时域的分析方法,即基于电路结构之间分析得到电路的S参数,举了一个简单的示例并给出了其对应的Matlab代码
5、电路综合-超酷-基于S11参数直接综合出微带线电路图
基于给定的S11参数的表达式综合出其对应的微带电路图,注意此处的S11参数表达式需要是解析形式(即要是函数表达式的形式)
6、电路综合-基于简化实频的SRFT微带线切比雪夫低通滤波器设计
基于切比雪夫函数进行电路综合,基于目标参数直接进行电路综合得到其对应的微带电路,给出了对应的理论与操作步骤(附Matlab代码)
7、电路综合-基于简化实频的SRFT微带线巴特沃兹低通滤波器设计
基于巴特沃斯函数进行电路综合,基于目标参数直接进行电路综合得到其对应的微带电路,给出了对应的理论与操作步骤(附Matlab代码)
8、电路综合-基于简化实频的SRFT微带线的带通滤波器设计
基于巴特沃斯与切比雪夫函数进行电路综合,基于目标参数直接进行电路综合得到其对应的带通的微带电路,给出了对应的理论与操作步骤(附Matlab代码)
9、电路综合-基于简化实频的任意幅频响应的微带电路设计
10、电路综合-基于简化实频的宽带匹配电路设计方法
阻抗匹配其实就是S11电路的匹配,给定需要匹配的阻抗数值去设计微带电路,其实就是给定了部分频点的S11参数去综合出电路图。我们唯一需要的就是根据部分频点的S11参数去拟合S11在理查德域的解析表达式。 这个拟合过程也可以看为一个优化过程,是为了使得解析表达式尽可能的接近已知的S11参数。其基本过程和9、电路综合-基于简化实频的任意幅频响应的微带电路设计一致。
但是,对于实际的电路,我们可能不会使用纯微带电路进行实现(很多模型的寄生参数往往都会等效为集总参数),可能需要用到集总参数和分布参数混合的方式,那么下面就首先来介绍一下集总参数电路综合的基本理论。
1、集总参数网络分析理论
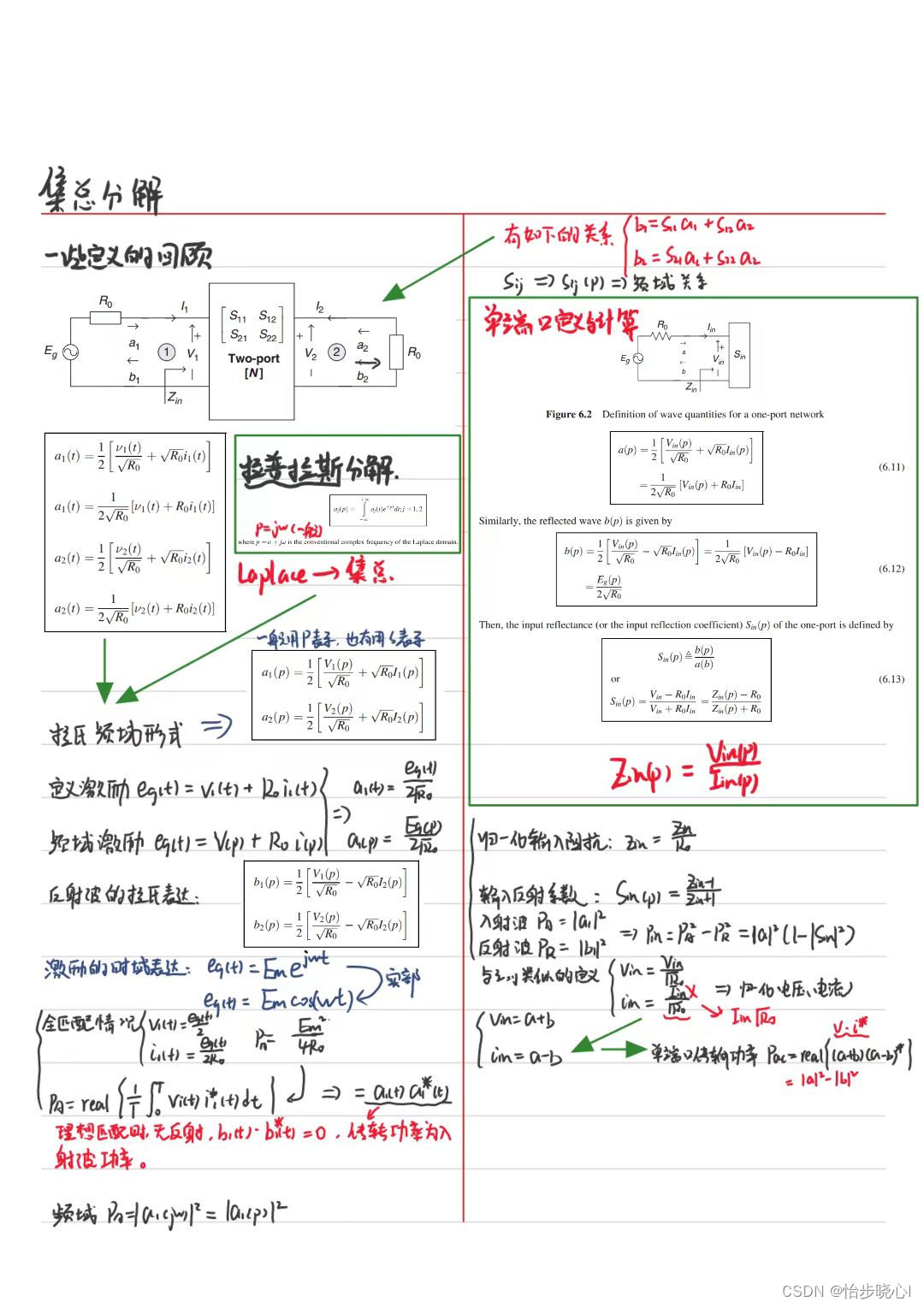
2、集总网络散射参数分析案例
对于如下的电路图,计算其输入阻抗和S11参数:
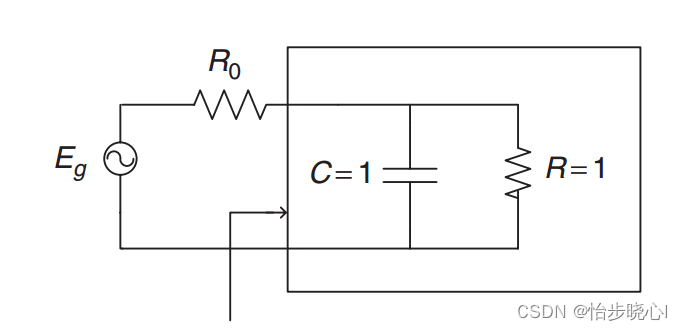
首先将集总器件转化为频域的分量,其输入阻抗可以使用下式进行计算:
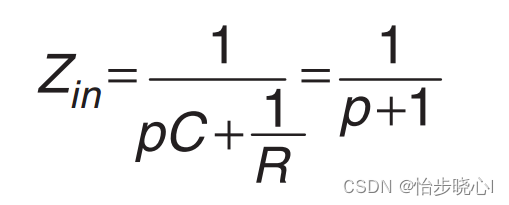
再使用下式就可以计算出其输入阻抗S11参数:
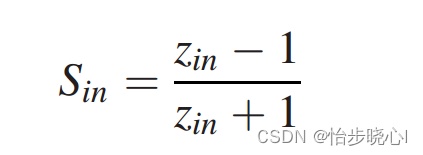
使用此思路,构建相应的matlab代码:
clear
clc
close allC=1;
R=1;
Z0=1;%求解频率范围,单位Hz
f_start=0.001;
f_stop=1;
f_step=0.001;
%求解范围
freq_solve=[f_start:f_step:f_stop];
w_solve=2*pi*freq_solve;
p=1j*w_solve;Zin=1./(p.*C+1/R);
Sin=(Zin-1)./(Zin+1);figure
plot(freq_solve/1e9,20*log10(abs(Zin)))
xlabel('Frequency(Hz)')
ylabel('dB(Zin)')
title('Zin')figure
plot(freq_solve/1e9,20*log10(abs(Sin)))
xlabel('Frequency(Hz)')
ylabel('S11')
title('S11')运行结果如下所示:
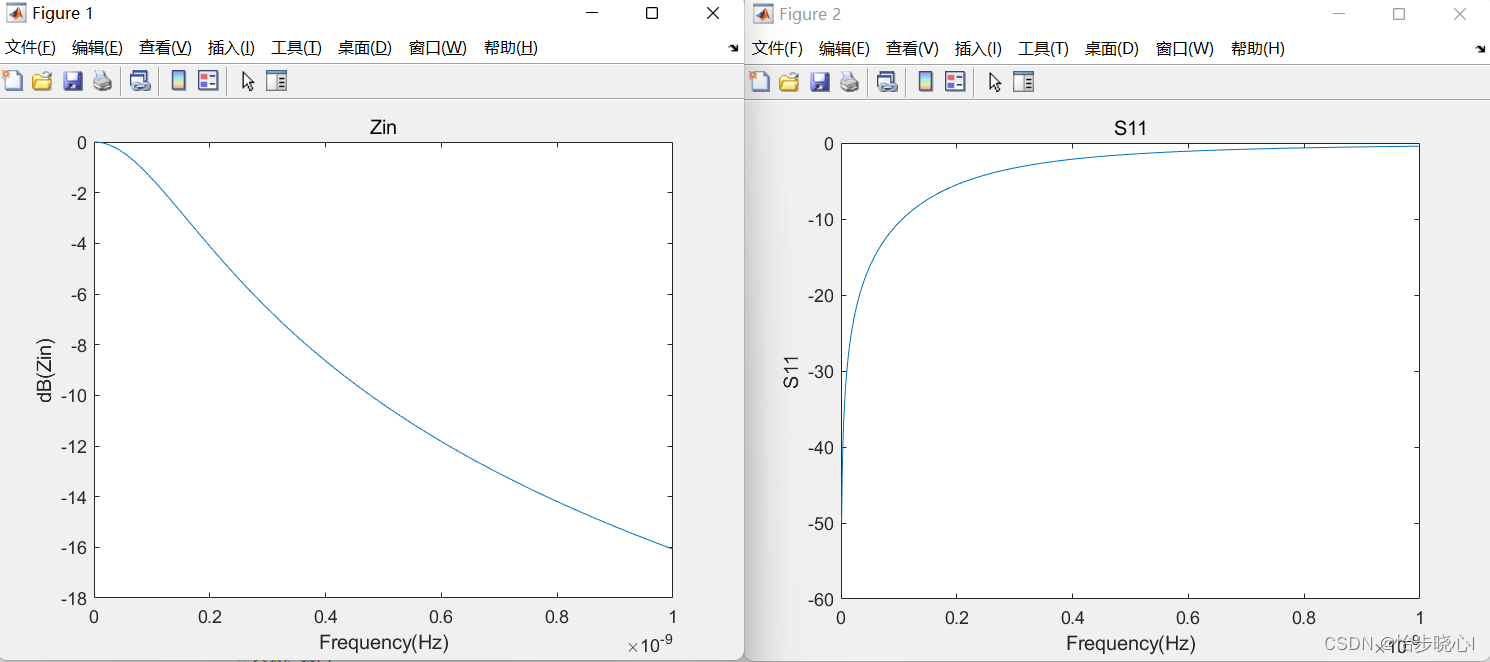
3、集总网络散射参数分析案例验证
使用ADS构建如下电路图:
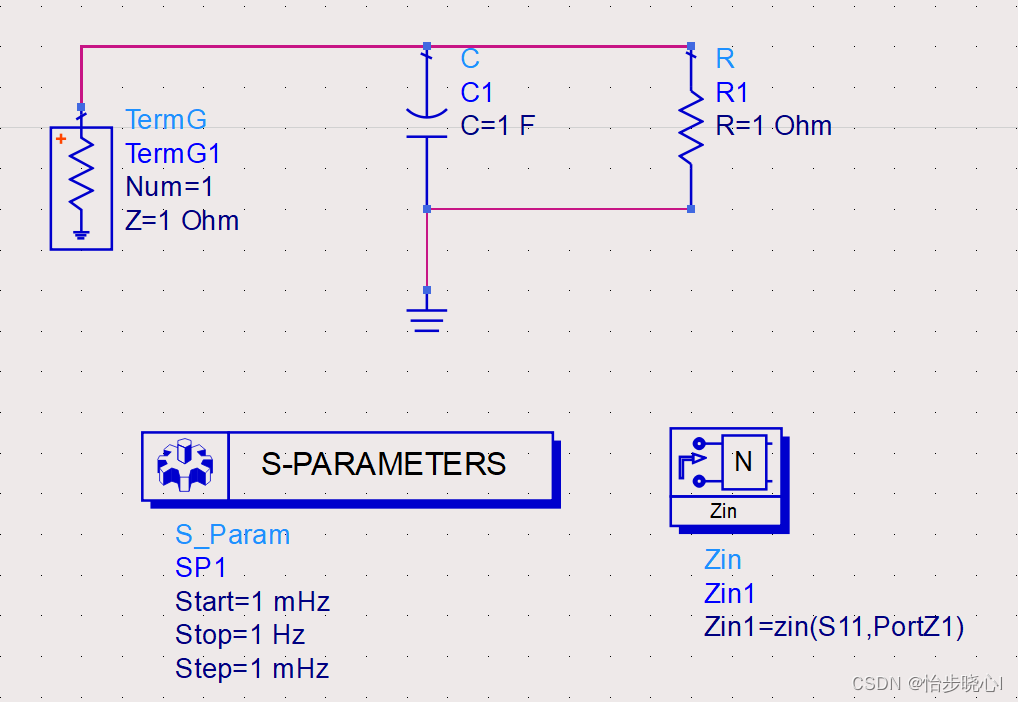
运行仿真,得到的结果与之前分析的一致:
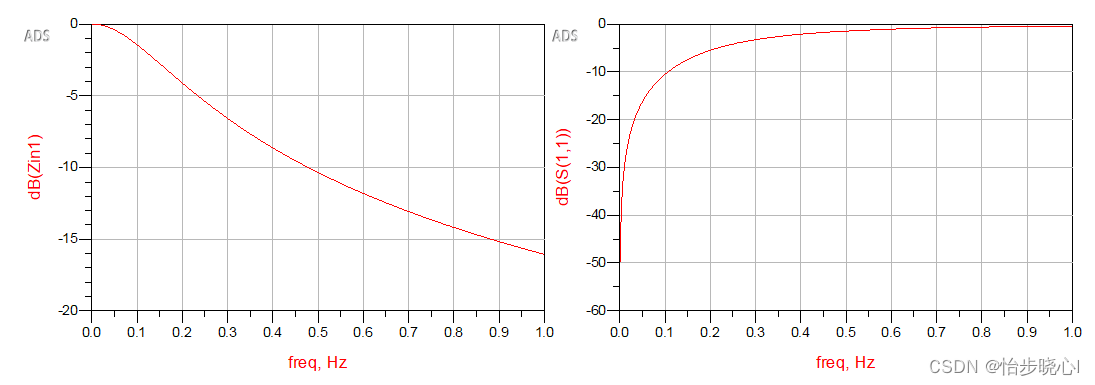
相关文章:

11、电路综合-集总参数电路结构的S参数模型计算与Matlab
11、电路综合-集总参数电路结构的S参数模型 电路综合专栏的大纲如下: 网络综合和简化实频理论学习概述 前面介绍了许多微带线电路综合的实际案例,如: 3、电路综合原理与实践—单双端口理想微带线(伪)手算S参数与时域…...

计算机网络--真题
因特网上专门用于传输文件的协议是 因特网上专门用于传输文件的协议通常是 FTP(File Transfer Protocol)。FTP 是一种标准的网络协议,用于在计算机之间传输文件。它允许用户在客户端和服务器之间传输文件,上传文件到服务器或从服务…...
java毕业设计基于ssm的招聘求职网站
项目介绍 本前途招聘求职网站是针对目前仓库的实际需求,从实际工作出发,对过去的前途招聘求职网站存在的问题进行分析,完善用户的使用体会。采用计算机系统来管理信息,取代人工管理模式,查询便利,信息准确…...
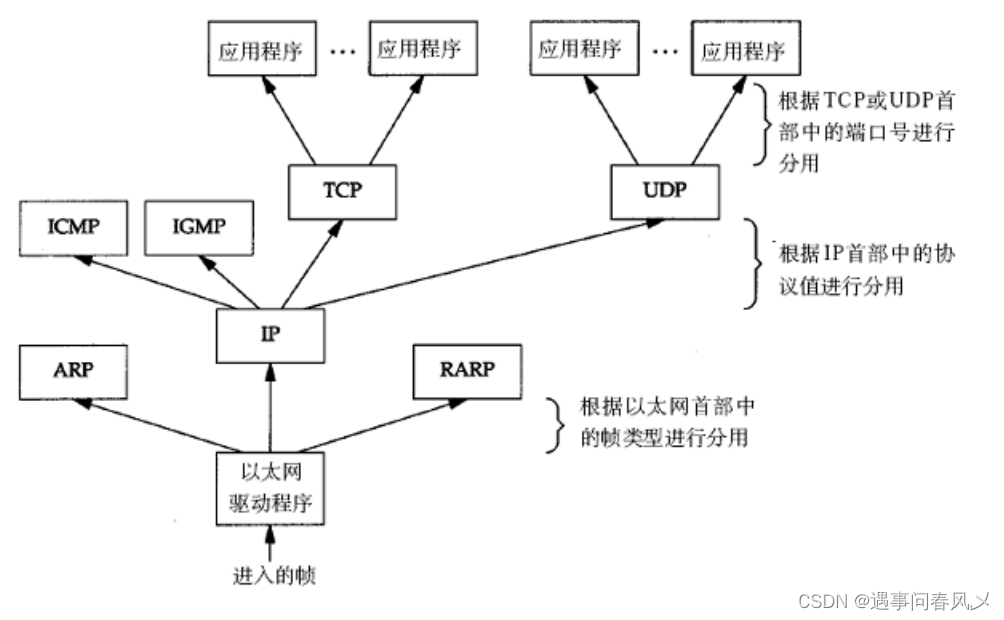
【JavaEE初阶】 初识网络原理
文章目录 🌲网络发展史🚩独立模式🚩网络互连📌局域网LAN🎈基于网线直连🎈基于集线器组建🎈基于交换机组建🎈基于交换机和路由器组建 📌广域网WAN 🍀网络通信基…...

LeetCode题解:993. 二叉树的堂兄弟节点,BFS,JavaScript,详细注释
原题链接: https://leetcode.cn/problems/cousins-in-binary-tree/ 解题思路: 使用队列进行BFS搜索,同时保存每个节点,以及其深度和父节点信息。当搜索到x和y时,对比深度和父节点,如果满足要求࿰…...
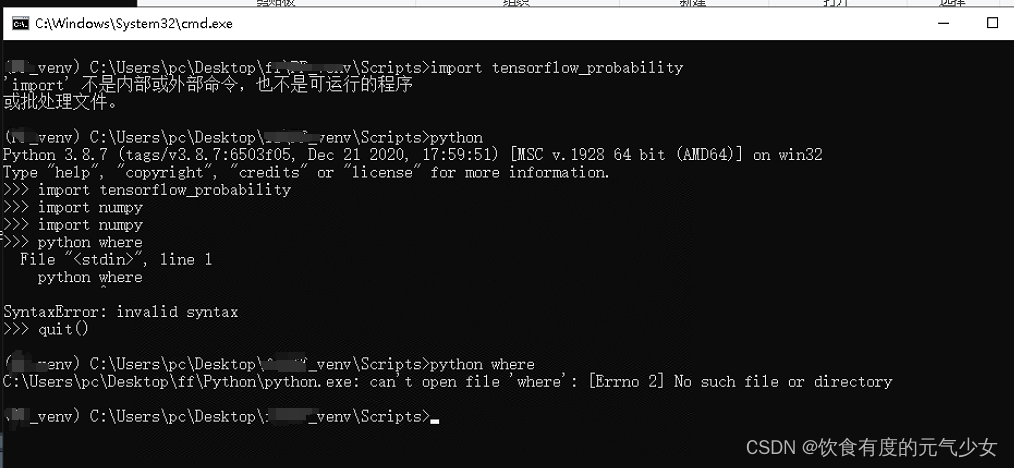
在python中加载tensorflow-probability模块和numpy模块
目录 操作步骤: 注意: 问题: 解决办法: 操作步骤: 在虚拟环境的文件夹中,找到Scripts文件夹,点击进去,找到地址栏,在地址栏中输入cmd,进入如下界面。 输…...

t2017递推2猴子摘桃
2、猴子摘桃(nhoi2005xx1) Description 果园里种了很多桃树,当桃树开始结果的时候,猴子便会成群结队地前来摘桃。 猴子们第一天会摘掉桃子的一半还多一个,第二天再摘第一天剩下的一半还多一个,以后每天均摘掉上一天剩下的一半还…...
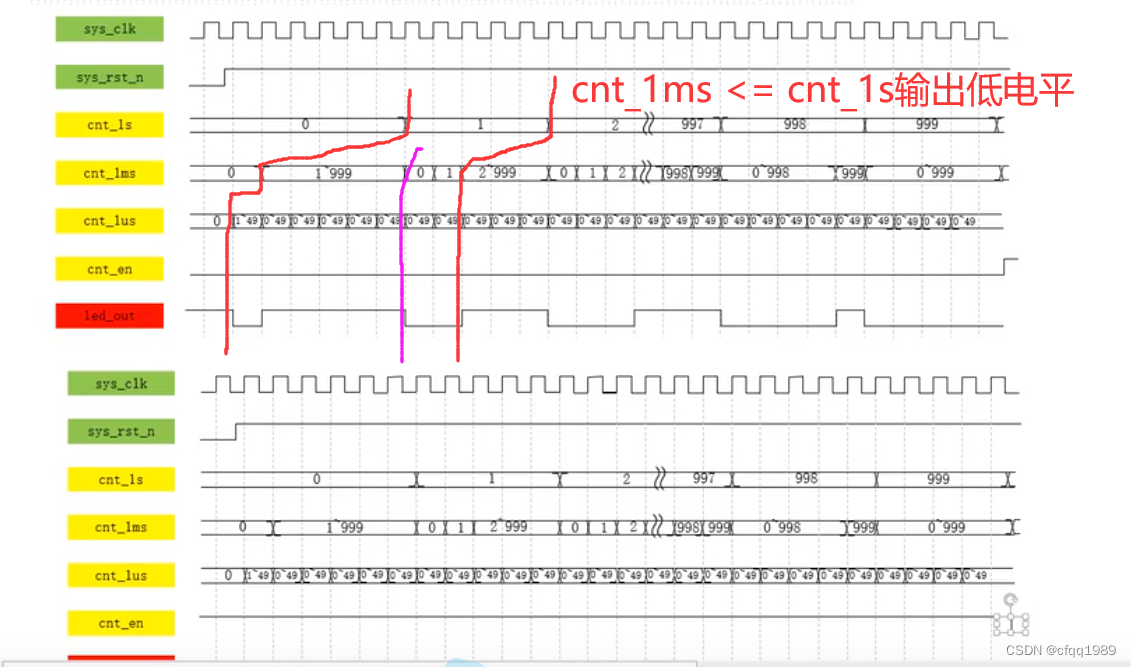
呼吸灯【FPGA】
晶振50Mhz 1us 等于 计0~49 1ms等于 0~999us 1s等于 0~999ms //led_outalways(posedge FPGA_CLK_50M_b5 or negedge reset_e8) //【死循环】敏感【触发条件:上升沿 clk】【运行副本】if(reset_e81b0)begin //50Mhz晶振, 49_999_999 是 1秒…...

Codeforces 1855E 数学期望 + DP
题意 传送门 Codeforces 1855E Expected Destruction 题解 将 S i S_i Si 运动至 S i 1 S_{i1} Si1 的情况看作后者消失,则 S i S_i Si 在碰到 S i 1 S_{i 1} Si1 前, S i 1 S_{i 1} Si1 必然存在。 根据数学期望的线性性质&…...

5-1CComplex运算符重载为友元
以下是一个用运算符重载为友元重载的方法重做复数加减法的运算,请填空完成程序。 #include <iostream> using namespace std; class CComplex { private:double real; double imag; public:CComplex(double r0.0,double i0.0){ real(r), imag(i)}friend…...

Vue3.0 watch和watchEffect监听器:VCA
简介 在项目中,有时候检测一个变量的值是否反升了变化。通常使用的watch或者使用低效的循环判断。 在次vue中给我们设置了深度监测数据繁盛变化的方法。 1.vue中提供了在watch监听时设置deep:true 就可以实现对对象的深度监听; 2.immediate:true,代表watch里面声明了…...

1360. 日期之间隔几天
1360. 日期之间隔几天 Java代码: 【DateFormat】DateFormat用于实现日期的格式化 import java.text.DateFormat; import java.text.ParseException; import java.text.SimpleDateFormat; import java.util.Date; // 好像已过时class Solution {public int daysBet…...
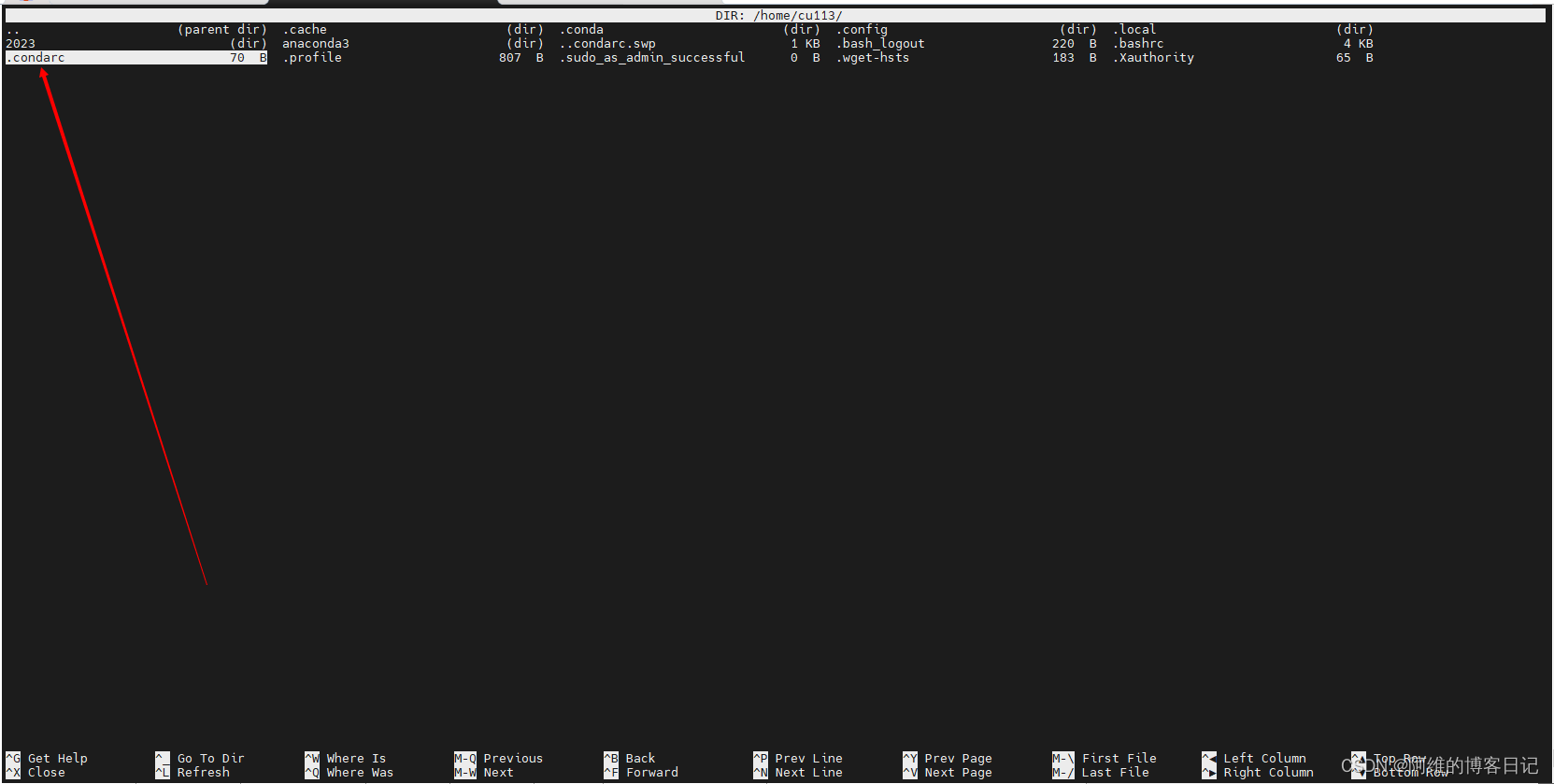
ubuntu配置 Conda 更改默认环境路径
我的需求是以后凡是新建一个虚拟环境都需要安装在一个挂载了大容量的分区/data里面 /home里面的是即将爆满但是还能塞点东西的硬盘. 如果您想要永久更改 Conda 的默认环境路径,可以编辑 Conda 的配置文件。首先,找到 Conda 的配置文件通常是 .condarc 文…...
华山编程培训中心——工业相机飞拍
飞拍功能是一种高速运动图像采集技术,通过降低相机的曝光时间来拍摄快速移动的对象,以提高工作效率和加快生产速度。下面视频演示工业相机飞拍: 上位机控制工业相机飞拍演示 一. 飞拍对相机硬件的要求 全局快门相机:飞拍要求相机…...

linux 释放缓存命令并做成定时任务
这个命令组合可以实现将待写入的数据同步到磁盘中,然后释放页面缓存。具体命令为: sync; echo 1 > /proc/sys/vm/drop_caches 第一个命令 sync 是将所有待写入磁盘的数据刷新到磁盘中,确保数据写入完成。第二个命令 echo 1 > /proc/…...
求解一个整数中含多少个1
1.问题描述:给定一个整数,统计其对应的二进制中含有1的个数。比如8(0000 1000),对应的二进制数中,只含有一个1. 2.设计思路:对x取余:zx%2。如果z!0,说明x的末尾不是为1.对于一个二进制x4x3x2x1…...

js编写一个函数判断所有数据类型
一、typeof 在 JavaScript 里使用 typeof 来判断数据类型,只能区分基本类型,即 “number”,”string”,”undefined”,”boolean”,”object” 五种。 对于数组、对象来说,其关系错综复杂&…...
)
Python对于时间相关模块的学习记录(time,datetime等模块)
1,time.time() 获得从计算机开始出生到现在的秒数(也成时间戳),可以时间相减计算流逝时间 说明 :擅长时间相减计算流逝时间 导入方法 import time import time# 1,time.time 获得从计算机开始出生到…...

【C#】获得所有可见窗口信息
【背景】 由于自己的瘦客户端上的Windows自带截图软件功能被阉割,所以自己写了一个,其中有窗口截图功能,涉及到获得所有可见窗口的信息。 【代码】 public WindowInfo[] GetAllDesktopWindows(){//用来保存窗口对象 列表List<WindowInf…...

ffmpeg的基本功能介绍
之前对ffmpeg有一个模糊的印象,后来经过一些项目对ffmpeg有了深入的认识,这里总结下。 最开始对ffmpeg的印象是可以对视频进行一些处理操作,但是做哪些操作又不是很清楚,知其然不知其所以然。下面对于ffmpeg的功能进行一个总结&a…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
