Python解题 - CSDN周赛第32期 - 运输石油(三维背包)
上期周赛因为最后一题出现bug,再加上都是经典的模板题,问哥就懒得写题解了。
本期也是有两道考过的题目,不过最后一题因为考到了背包问题的特殊类型,还是值得拿出来记个笔记。
第一题:传奇霸业
传奇霸业,是兄弟就来干。小春(HP == a)遇到了一只黄金哥布林(HP == x)。小春每次能对哥布林造成b点伤害,哥布林每次能对小春造成y点伤害。作为玩家的小春怎么可能随便让哥布林打死呢!他有治疗神药,每次能恢复c点HP。HP无上限。小春需要操作多少次才能打死哥布林?(治疗+攻击)
输入描述:第一行输入a,b,c。(1<=a,b,c<=1000)。第二行输入x,y。(1<=x<=1000,0<=y<c)
输出描述:输出最小操作次数。
示例:
示例 输入 11 6 100
12 5输出 2
分析
模拟。但本题出得不是特别好,因为对游戏的流程没有说清楚。不管有没有玩过游戏,读完此题都会有一定程度的迷惑:是先攻击怪物(哥布林)还是先受攻击?是回合制还是即时制(在被攻击前可以无限吃药)?问哥一开始以为是即时制,所以最初的思路是一旦自己的HP小于怪物的攻击力,就不断吃药,直到大于怪物攻击力。。。然后无法通过,才发现原来是回合制。修正思路为:如果自己的HP大于怪物的攻击力,或怪物的HP小于自己的攻击力(一击毙命,没必要浪费回合回HP),则发动一次攻击;否则就吃一次药恢复HP。然后轮到怪物发动一次攻击,自己的HP减去怪物的攻击力,然后循环直到怪物HP小于等于0。最后循环的次数就是答案。
参考代码
a, b, c = map(int, input().strip().split())
x, y = map(int, input().strip().split())
res = 0
while x > 0: # 循环直到怪物体力小于等于0if a > y or b >= x: # 如果自己的HP大于怪物的攻击力,或者怪物的HP小于自己的攻击力x -= b # 选择攻击else:a += c # 选择吃药回复HPres += 1 # 回合加一a -= y # 自己受到怪物的攻击,HP减少
print(res)第二题:严查枪火
X国最近开始严管枪火。像是“ak”,“m4a1”,“skr”。都是明令禁止的。现在小Q查获了一批违禁物品其中部分是枪支。小Q想知道自己需要按照私藏枪火来关押多少人。(只有以上三种枪被视为违法)
输入描述:第一行输入整数n.(1<=n<=10000)表示携带违禁物品的人数。以下n行表示违禁物品的名称。
输出描述:输出需要按照私藏枪火来关押的人。
示例:
示例 输入 3
Dsd
ak
232asd输出 1
分析
第6期考过的老题,以前也写过题解。
没什么好分析的,就是依次检查列表中的字符串是否等于这三种枪火所代表的字符串,最后输出相等的个数即可。
参考代码
n = int(input().strip())
res = 0
for _ in range(n):temp = input().strip()if temp in {"ak", "m4a1", "skr"}:res += 1
print(res)第三题:蚂蚁家族
小蚂蚁群是一个庞大的群体,在这个蚂蚁群中有n只小蚂蚁 ,为了保证所有蚂蚁在消息传送的时候都能接收到消息,需要在他们之间建立通信关系。就是要求小蚂蚁都可以通过多只或者直接联系到其他人。已知几条小蚂蚁之间有通信关系,请问还需要再新建至少多少条关系?
输入描述:第一行输入整数n,m;n为小蚂蚁总数;m为关系数。(1<=n,m<=1000)。以下m行每行m对整数x,y。(代表x与y有联系)
输出描述:输出最少需要新建关系数。
示例:
示例 输入 4 3
1 2
2 3
3 4输出 0
分析
第12期考过(好像并不遥远),可以参考以前写的题解。
官方很喜欢考并查集,问哥当初解这道题的时候,是靠着测试用例的缺陷骗分过了。后来又自己琢磨了使用集合的方法,不过这次再次遇到,就可以用已经熟悉的并查集模板来解了。
算法原理还是一样,先定义并查集的查集函数find(),再把每次输入边的顶点合并在一起,都指向同一个“祖先”,最后统计祖先的个数,就表示了现在已存在的连通子图的个数,要把它们连在一起,只需要个数减一条边就可以了。
参考代码
n, m = map(int, input().strip().split())
ants = list(range(n+1))
def find(i):if ants[i] == i: return iants[i] = find(ants[i])return ants[i]
for _ in range(m):a, b = map(int, input().strip().split())ants[find(a)] = find(b)
result = set()
for i in ants[1:]:j = find(i)result.add(j)
print(len(result)-1)不过比赛中本题的数据有坑,有一个测试数据的节点编号超过了 n,于是在查集的时候报了下标越界的错误, 所以上面的代码要稍微修改一下。只要增加一个节点,最后再判断该节点有没有边即可。
第四题:运输石油
某石油公司需要向A、B两地运输石油。两地的需求量不同,而一辆车只能装载一定量的石油。经过计算A地需要a辆车,B地需要b辆车运输才能满足需求。现在一共有n辆车分布在各地,每辆车前往A、B两地运输石油均可以获得一定不等的利润。现在请你安排a辆车前往A地,b辆车前往B地运输石油,使得在满足A、B两地石油需求的前提下,获得最大的利润。每辆车只能前往一地运输石油。
输入描述:输入第一行包含三个整数n,a,b,分别表示公司的车辆数量和A,B两地车辆所需数量,保证a+b<=n。(1<=n<=1000)。接下来有n行,每行两个正整数x,y,分别表示该车完成A地任务的利润和B地任务的利润。
输出描述:输出仅包含一个正整数,表示最大获得的利润和。
示例:
示例 输入 5 2 2
4 2
3 3
5 4
5 3
1 5输出 18
分析
题目本身不太难,难的是对测试数据的优化。
从题干来看,还是背包问题的一个扩展子类:三维背包问题。也就是,存在两个背包(A地和B地,两地需要的车的数量类似于普通背包的容积),怎样分配物品(n辆车,类似于体积)才能得到最优解(最大价值)。
既然是背包问题,就存在状态转移。我们可以用 的三维数组来表示
辆车中有
辆去往A地,
辆去往B地的最大价值。那我们如果增加了一辆车,也就是检查第
辆车的时候,
的值怎样得到呢?这时,我们有三个选择:
- 不派这辆车,那么
- 派这辆车去A地,那么
(因为这辆车去了A地,那么前面
辆车里就少派一辆去A地的车)
- 派这辆车去B地,那么
(同上,因为这辆车去了B地,那么前面
辆车里就少派一辆去B地的车)
很显然,最终 的值就等于这三项最大值。于是,可以得到状态转移方程如下:
如果熟练掌握了基础背包问题,这里很容易就可以看出:因为在状态转移时只用到了 ,所以可以类似01背包,使用循环数组降低空间复杂度,减去一维。但是同样地,状态转移的时候,需要逆序更新。
降维后的转移方程如下:
所以,到这里我们关于这道题的解法已经很清楚了,代码整理如下:
参考代码一
n, a, b = map(int, input().strip().split())
dp = [[0]*(b+1) for _ in range(a+1)]
for i in range(1, n+1):profit_a, profit_b = map(int, input().strip().split())for j in range(a, -1, -1): # 因为使用了滚动数组优化空间,需要逆序更新for k in range(b, -1, -1): # 同上if j > 0: dp[j][k] = max(dp[j][k], dp[j-1][k]+profit_a)if k > 0: dp[j][k] = max(dp[j][k], dp[j][k-1]+profit_b)
print(dp[a][b])这里要注意边界问题,也就是当 或
时,无须从
或
的状态更新过来。
然鹅,上面的代码是无法pass这道题的。原因就在于测试数据范围太大,而我们的算法时间复杂度是 ,其中
,而测试数据的范围在 1e4,计算量级相当于1e12 (
)。必须考虑优化。
优化
不幸的是,关于三维背包,问哥并不知道是否存在能够优化时间复杂度到 甚至更低的算法。但是上面的状态转移过程中,很显然存在很多无意义的计算,也就是派往A地和B地的车的数量存在
的限制。于是,可以通过剪枝来进行一定的优化。
在下面两行代码里,、
分别代表派往A地和B地的车的数量,而这两个数量的范围使用了
和
。
for j in range(a, -1, -1): for k in range(b, -1, -1): 不难发现,当我们只有 辆车的时候:
- 如果
,我们最多只能派
辆,而不是
辆车,去往A地;
- 如果
,我们最多也只需要派
辆车去A地。
所以,我们派往A地的车辆数量的上限是 。
同样地,因为我们在 辆车里选择了
辆去A地,那么我们最多只能派
辆车去往B地。所以派往B地车辆数量的上限是
。
我们再来看范围的下限。常识里,下限应该是0,也就是一辆都不派,但真的是这样吗?
本题所谓的下限,也就是在 辆车里最少派多少辆车到两地。以A地为例,因为题目要求一定要派
辆车到A地,那么我们在
辆车里最少要派的
辆车,加上剩下的最多能派往A地的车,必须要等于
。剩下的
辆车里最多也只能派
辆车,也就是全部派往A地,所以最小的
要满足
。显然,如果
,也就是说剩下的车辆数量大于等于
的话,
的最小值是 0。于是,可以得到
的下限是
。
再来看B地。同样的道理,题目要求一定要派 辆车到B地,也就是说,我们在
辆车里最少要派的
辆车,加上剩下的最多能派往B地的车,必须要等于
。但是,考虑到剩下的车里至少要保留
辆会派往A地,所以剩下能派往B地的车数量最多只有
辆。于是,最小的
要满足
。展开,可以得到
的下限是
。
而在此上下限范围之外的数据,我们是压根不需要计算的。因为逻辑不合理,它们对最终结果不会产生影响,于是我们可以进行剪枝。 更新代码,最终得到pass代码如下:
参考代码二
n, a, b = map(int, input().strip().split())
dp = [[0]*(b+1) for _ in range(a+1)]
for i in range(1, n+1):aa, bb = map(int, input().strip().split())for j in range(min(i, a), max(0, a-n+i)-1, -1):for k in range(min(i-j, b), max(0, b-n+a+i-j)-1, -1):if j > 0: dp[j][k] = max(dp[j][k], dp[j-1][k]+aa)if k > 0: dp[j][k] = max(dp[j][k], dp[j][k-1]+bb)
print(dp[a][b])由此可见,虽然算法的渐进时间复杂度没有改变,但是通过剪枝,还是可以通过测试用例,说明测试数据中存在许多干扰的无用数据,想必这也是考点之一吧。
相关文章:
Python解题 - CSDN周赛第32期 - 运输石油(三维背包)
上期周赛因为最后一题出现bug,再加上都是经典的模板题,问哥就懒得写题解了。 本期也是有两道考过的题目,不过最后一题因为考到了背包问题的特殊类型,还是值得拿出来记个笔记。 第一题:传奇霸业 传奇霸业,是…...
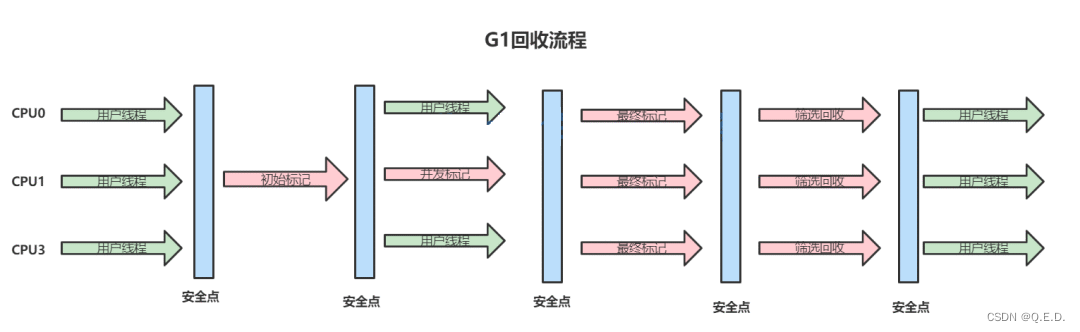
JVM - G1垃圾收集器深入剖析
1、G1收集器概述 HotSpot团队一直努力朝着高效收集、减少停顿(STW: Stop The World)的方向努力,也贡献了从串行Serial收集器、到并行收集器Parallerl收集器,再到CMS并发收集器,乃至如今的G1在内的一系列优秀的垃圾收集器。 G…...

角度制与弧度制的相互转换np.deg2radnp.rad2deg
【小白从小学Python、C、Java】【计算机等级考试500强双证书】【Python-数据分析】角度制与弧度制的相互转换np.deg2radnp.rad2deg选择题以下关于python代码表述错误的一项是?import numpy as npprint("【执行】np.rad2deg(np.pi)")print(np.rad2deg(np.pi))print(&…...
)
【SAP Abap】X-DOC:SAP ABAP 语法更新之一(Open SQL新增特性)
SAP ABAP 语法更新之一(Open SQL新增特性)1、前言2、演示1、前言 自从 SAP 推出 SAP ON HANA,与之相随的 AS ABAP NW 7.40 版本以后,ABAP 语法也有了较多的更新,本篇对 Open Sql的语法更新部分做一个DEMO演示。 NW 7…...

【改进灰狼优化算法】改进收敛因子和比例权重的灰狼优化算法【期刊论文完美复现】(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

Linux C代码获取线程ID
Linux C代码获取线程ID gettid可以获取线程id,但是通过man gettid可以看到下面这两句 也就是说glibc没有为这个gettid封装系统调用,需要使用syscall。 #define _GNU_SOURCE#include <unistd.h>#include <sys/syscall.h>#include <sys/types.h>pi…...
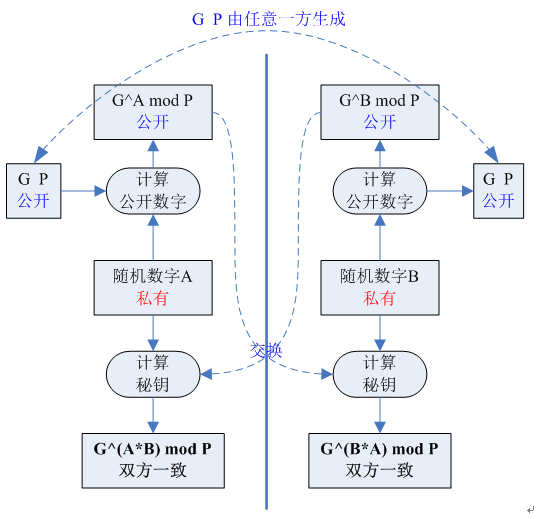
基本密码技术
AESAES取代DES,是一种对称加密技术,分为AES-128/192/256, 其分组长度固定为128b,若最后一个分组长度不够,需要补全至128b长度。所支持的秘钥长度分别为128b/192b/256b.分组密码模式AES是对明文进行分组之后逐块进行加密࿰…...
【力扣周赛#334】6369. 左右元素和的差值 + 6368. 找出字符串的可整除数组 + 6367. 求出最多标记下标
目录 6369. 左右元素和的差值 - 前缀后缀和 ac 6368. 找出字符串的可整除数组 - 操作余数ac 6367. 求出最多标记下标 - 二分答案 贪心 6369. 左右元素和的差值 - 前缀后缀和 ac class Solution {public int[] leftRigthDifference(int[] nums) {int nnums.length;int[] re…...
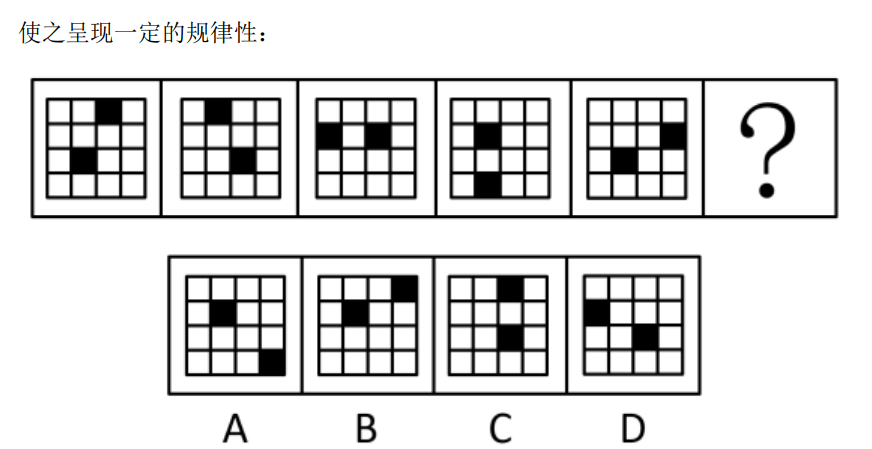
行测-判断推理-图形推理-位置规律-平移
位置平移,选D空白每次顺时针移动一格,黑色圆每次逆时针移动2格选C两个黑色⚪,每次顺时针移动2格白色⚪,先到对角位置,再顺时针移动一格选B三角形的底,顺时针移动三角形的顶点,在正方形的内部顺时…...
)
数据库基础知识(一)
目录 什么是数据库 表,列,行 主键 什么是SQL 什么是数据库 数据库(database):保存有组织的数据的容器(通常是一个文件或一组文件)。 数据库软件(DMBS):又名数据库管理系统。数据库是通过数据库软件创建和操纵的容器。因为你并…...
MyBatis 的工作原理解析
文章目录前言一、mybatis工作原理1.1 流程图1.2 步骤解析1.3 代码实现前言 本文记录 Mybatis 的工作原理,做到知识梳理总结的作用。 一、mybatis工作原理 Mybatis 的总体工作原理流程图如下图所示 1.1 流程图 1.2 步骤解析 Mybatis 框架在工作时大致经过8个步骤…...
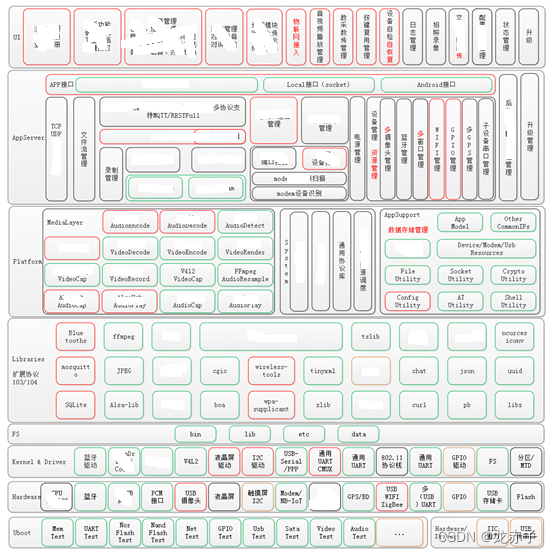
终端软件架构说
目录 零:前言 一,基于服务的架构 二,基于多进程多线程的架构 三,以数据为中心的架构 四,类Android的分层架构设计 五,总结 零:前言 谈到架构,可能大家的第一感觉是信息系统的…...

LearnOpenGL-入门-你好,三角形
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject LearnOpenGL中文官网:https://learnopengl-cn.github.io/ 文章目录图形渲染管线基本介绍着色器…...

SOEM 源码解析 ecx_init_redundant
/* Initialise lib in redundant NIC mode* 在冗余网卡模式下初始化lib库* param[in] context context struct* 上下文结构体* param[in] redport pointer to redport, redundant port data* 指向冗余端口的指针ÿ…...
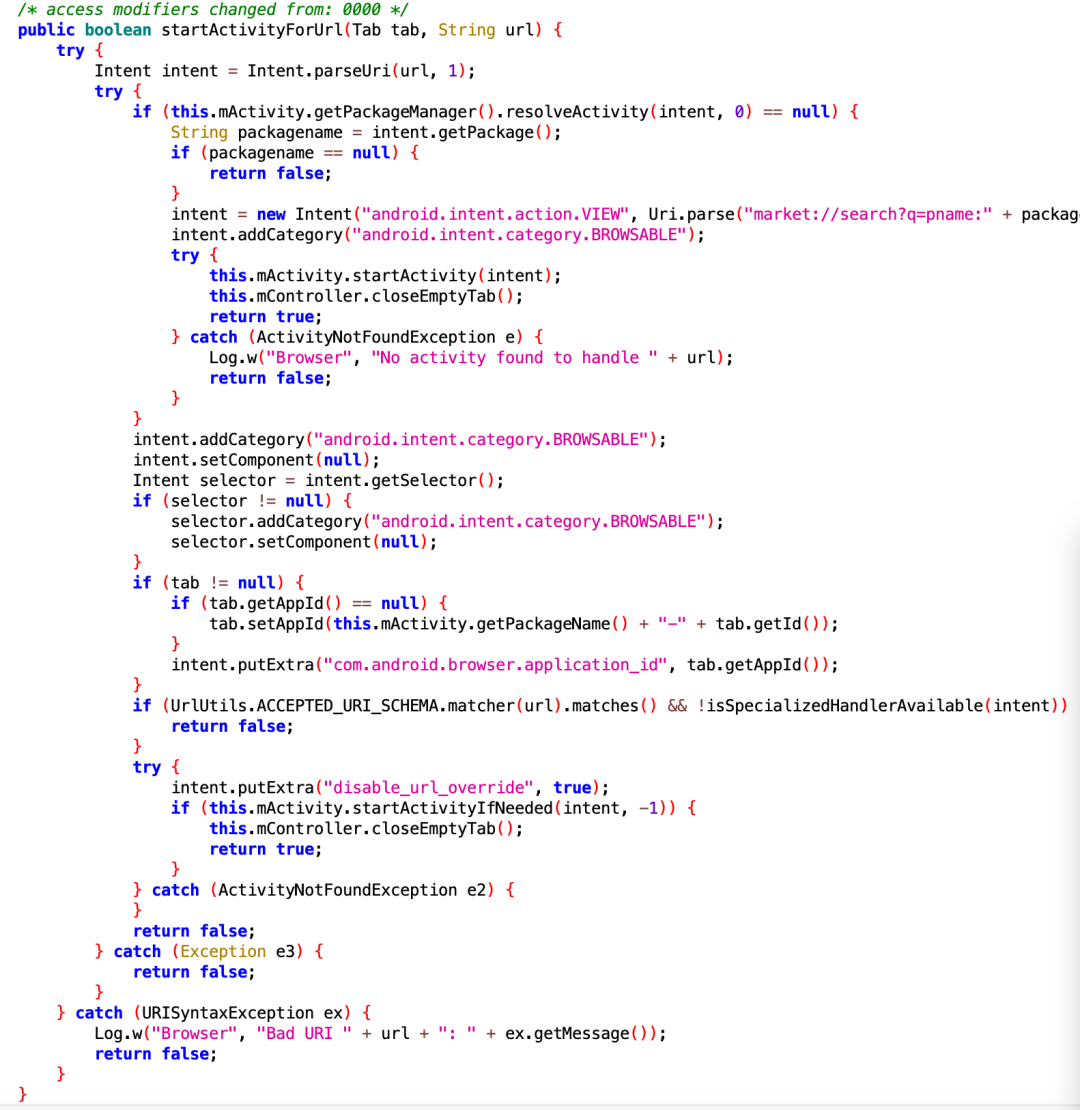
网页唤起 APP中Activity的实现原理
疑问的开端大家有没有想过一个问题:在浏览器里打开某个网页,网页上有一个按钮点击可以唤起App。这样的效果是怎么实现的呢?浏览器是一个app;为什么一个app可以调起其他app的页面?说到跨app的页面调用,大家是…...
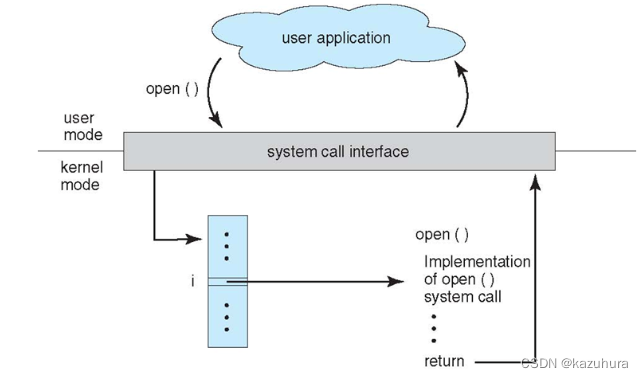
【操作系统】概述
基本特征 1. 并发 并发是指宏观上在一段时间内能同时运行多个程序,而并行则指同一时刻能运行多个指令。 并行需要硬件支持,如多流水线、多核处理器或者分布式计算系统。 操作系统通过引入进程和线程,使得程序能够并发运行 2. 共享 共享…...
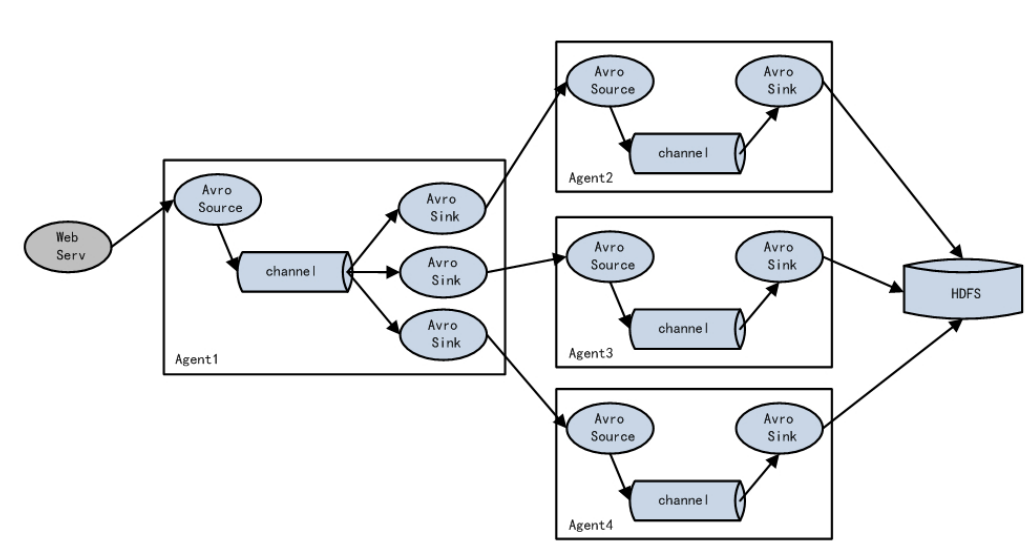
Flume三种组件的选择对比
文章目录1.source2.channel3.sink1.source Source: 数据源:通过source组件可以指定让Flume读取哪里的数据,然后将数据传递给后面的 channel Flume内置支持读取很多种数据源,基于文件、基于目录、基于TCP\UDP端口、基于HTTP、Kafka的 等等、当然了&#x…...

响应性基础API
一.什么是proxy和懒代理?什么是proxy?proxy对象是用于定义基本操作的自定义行为(如:属性查找,赋值,枚举,函数调用等等)。什么是懒代理?懒代理:在初始化的时候不会进行全部代理,而是…...

剑指 Offer 25. 合并两个排序的链表
剑指 Offer 25. 合并两个排序的链表 难度:easy\color{Green}{easy}easy 题目描述 输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。 示例1: 输入:1->2->4, 1->3->4 输出:1…...

顿悟日记(一)
目录2023年1月顿悟日记:2023年2月24日顿悟日记:2023年2月25日顿悟日记:2023年2月26日顿悟日记:顿悟的经历是如此的奇妙,且让人亢奋的事情。 2023年1月顿悟日记: 1.我是面向对象还是面向过程? …...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
