代碼隨想錄算法訓練營|第五十八天|583. 两个字符串的删除操作、72. 编辑距离、编辑距离总结篇。刷题心得(c++)
目录
讀題
583. 两个字符串的删除操作
自己看到题目的第一想法
看完代码随想录之后的想法
72. 编辑距离
看完代码随想录之后的想法
583. 两个字符串的删除操作 - 實作
思路
代碼隨想錄思路
Code
72. 编辑距离 - 實作
思路
Code
编辑距离总结篇
判斷子序列
不同的子序列
兩個字符串的刪除操作
編輯距離
總結
判斷子序列
不同子序列
兩個字符串的刪除操作
編輯距離
讀題
583. 两个字符串的删除操作
自己看到题目的第一想法
如果今天可以兩個都刪除,那在w1[i - 1] 以及 w2[j - 1]的狀況下有三種狀況,兩者匹配,dp[i - 1][j - 1],不使用w1[i - 1]→dp[i - 1][j] 不使用w2[j - 1] → dp[i][j - 1],有用畫圖的方式嘗試理解但仍然無法推出狀態的改變。
看完代码随想录之后的想法
看完之後,才真正了解自己哪裡錯了,首先下標就定義錯了,下標應該是dp[i][j] w1[i - 1]為結尾以及w2[j - 1]為結尾如果想要達到相等,所需要刪除元素的最少次數為dp[i][j]
根據這個定義,如果相等的時候,不用刪除元素,那就會等於不包含當前i - 1 j - 1的 i - 2 j - 2,也就是dp[i][j] = dp[i - 1][j - 1]
如果不相等,則會有三種狀況可以刪除w1 最少操作次數就是不包含當前的w[i - 1]的狀況也就是dp[i - 1][j] + 1 也可以選擇刪除w2 最少操作次數是dp[i][j - 1] + 1,不包含當前w2[j - 1]的最少狀況。
也可以兩個都刪除,也就是dp[i - 1][j - 1] + 2,但這個我們可以思考為,之前的兩種狀況就有包含了,如果刪除w1,那是取不包含w1[i - 1]的狀況,換言之,就是刪除w1[i - 1]的狀況是dp[i - 1][j] ,在這個基礎上再減去w2[j - 1]這一個數就是dp[i - 1][j] + 1。
最後可以簡化為dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
72. 编辑距离
看完代码随想录之后的想法
非常清晰,基本上有寫過之前的題目就會知道其中的門道,跟上一題一樣,先定義好dp[i][j]的定義,在下標word1[i - 1]以及下標word2[j-1],使其相同的最小編輯距離為dp[i][j]。
那就一樣會有兩種狀況相同與不相同
相同的話就是dp[i][j] = dp[i - 1][j - 1]代表不需要任何操作,跟上一次不包含word1[i - 1]以及word2[j - 1]的狀況一致
不相同的話要做增刪換
增和刪可以想成同樣一個,操作數都是一樣的,引用代碼隨想錄中提到的例子
word2添加一个元素,相当于word1删除一个元素,例如
word1 = "ad" ,word2 = "a",word1删除元素'd'和word2添加一个元素'd',变成word1="a", word2="ad", 最终的操作数是一样! dp数组如下图所示意的:0 a 0 a d+-----+-----+ +-----+-----+-----+0 | 0 | 1 | 0 | 0 | 1 | 2 |+-----+-----+ ===> +-----+-----+-----+a | 1 | 0 | a | 1 | 0 | 1 |+-----+-----+ +-----+-----+-----+d | 2 | 1 |+-----+-----+
替換的話代表只需要替換其中一個數就可以一致,那就會是dp[i][j] = dp[i - 1][j - 1] + 1,代表我只要替換word1 或者word2就可以使得兩者相同。使用dp[i - 1][j - 1]的緣故是,這個數不包含word1、或word2,所以如果只需要替換一個數就可以達成,那就是將這個數加一就好
583. 两个字符串的删除操作 - 實作
思路
-
定義DP數組以及下標的含意
i - 1 下標的word1以及 j - 1 下標的word2,要達到相同的子序列最少需要刪除多少次為dp[i][j]
-
遞推公式
分成兩種狀態相同與不相同
相同的話代表不用刪除,也就是dp[i - 1][j - 1]即為上一次不包含當前兩個數的狀況
不相同的話有三種狀況
- 刪除word1
- 代表不包含當前word1的狀況在加上一個刪除的個數也就是dp[i - 1][j] + 1
- 刪除word2
- 代表不包含當前word2的狀況再加上1個刪除數,也就是dp[i][j - 1] + 1
- 刪除word1、word2
- 代表不包含當前word1、word2的狀況加上兩個刪除數,也就是dp[i - 1][j - 1] + 2
- 但可以換個角度來看,如果刪除word1或word2時,我們要先得知不包含word1或word2的狀況,也就是dp[i - 1][j] 或 dp[i][j - 1] 也就是說這兩個狀態組都代表已經忽略word1 以及word 2時,當前的狀況,那在這個基礎上再加1,也可以理解為在忽略word1的狀況下在刪除word2 就會是將word1、word2都刪除的狀況,也就是dp[i - 1][j] + 1。
- 刪除word1
-
根據遞推公式、題意以及定義,確定DP數組如何初始化
因為兩者都可以刪除,所以在初始話時,空字符串都是0,因為不用刪除,其他的部分則根據當前的位置,刪除不同數量的word即可以成為空字符串,也就是要刪除i 個或j個字,字符串才會為空
-
確定遍歷順序
因為需要左上角的數據來進行遍歷,所以是由前往後。
代碼隨想錄思路
Code
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp (word1.size() + 1, vector<int>(word2.size() + 1, 0));for(int i = 0; i <= word1.size(); i++) dp[i][0] = i;for(int j = 0; j <= word2.size(); j++) dp[0][j] = j;for(int i = 1; i <= word1.size(); i++) {for(int j = 1; j <= word2.size(); j++) {if(word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];else dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);}}return dp[word1.size()][word2.size()];}
};
72. 编辑距离 - 實作
思路
-
定義DP數組以及下標的含意
i - 1 下標的word1以及 j - 1 下標的word2,要達到相同的子序列最少需要編輯多少次為dp[i][j]
-
遞推公式
分成兩種狀態相同與不相同
相同的話代表不用編輯,也就是dp[i - 1][j - 1]即為上一次不包含當前兩個數的狀況
不相同的話有三種狀況,取最小的
- 刪除\添加 word1
- 代表不包含當前word1的狀況在加上一個刪除\添加的個數也就是dp[i - 1][j] + 1
- 刪除\添加 word2
- 代表不包含當前word2的狀況再加上1個刪除\添加數,也就是dp[i][j - 1] + 1
- 替換
- 代表不包含當前word1、word2的狀況加上一個操作,也就是dp[i - 1][j - 1] + 1
- 刪除\添加 word1
-
根據遞推公式、題意以及定義,確定DP數組如何初始化
當j - 1以及 i - 1的word1、word2需要初始化時,需要刪除i個或j個字符才會等於空字符
-
確定遍歷順序
總共有四個遞推公式
dp[i][j] = dp[i - 1][j - 1]
dp[i][j] = dp[i - 1][j - 1] + 1
dp[i][j] = dp[i - 1][j] + 1
dp[i][j] = dp[i][j - 1] + 1
因為需要左上角的數據來進行遍歷,所以是由前往後。
Code
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp (word1.size() + 1, vector<int>(word2.size() + 1));for(int i = 0; i <= word1.size(); i++) dp[i][0] = i;for(int j = 0; j <= word2.size(); j++) dp[0][j] = j;for(int i = 1; i <= word1.size(); i++) {for(int j = 1; j <= word2.size(); j++) {if(word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];else dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;}}return dp[word1.size()][word2.size()];}
};
编辑距离总结篇
判斷子序列
定義: dp[i][j] 代表 i - 1 的s 和 j - 1 的t 相同子序列的長度為dp[i][j]
根據這個定義,我們可以知道當兩者相同時,長度要加一
如果不相等時,則可以視為忽略當下的t[j - 1]取t的前一個數也就是t[j - 2] → dp[i][j] = dp[i][j - 1]
不同的子序列
定義: dp[i][j]: 以i - 1為結尾s子序列當中,出現以j - 1為結尾t的個數為dp[i][j]
根據定義
-
兩者相等時有兩種狀況
我可以使用s[i - 1]也可以不使用s[i - 1] 因為定義是i - 1為結尾的s子序列中,出現以j - 1為結尾的t個數
所以在使用s[i - 1]的狀況,我不用刪除任何元素,所以我的值會是dp[i - 1][j - 1]即上一次的狀況,
如果不使用s[i - 1]的狀況,我等同於只需要不考慮s[i - 1] 但t[j - 1]仍然在,所以值會是dp[i - 1][j]
相同時的轉移方程就會是dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
-
兩者不相等時相當於s 要刪除元素,因為 s的字符串中,這個位置並沒有t的字串,所以要刪除
如果是s要刪除元素,那就是取s[i - 2] 這個不包含s[ i -1]的最大值,但t是要比較的子序列,所以t不用動,也就是說這個dp[i][j]會是由s[i - 2]t[j - 1]所組成,所對應的dp數組是dp[i][j] = dp[i - 1][j]。
初始化:
dp[i][0] 一定都是1,因為把s全部刪除後出現空字符的個數就是一
dp[0][j] 因為s無論如何都無法變成t,所以都是0
dp[0][0] 空字符串s可以刪除0個元素變成空字符串t,所以等於1
兩個字符串的刪除操作
定義: i - 1 下標的word1以及 j - 1 下標的word2,要達到相同的子序列最少需要刪除多少次為dp[i][j]
根據這個定義轉移方程會有兩個狀況
- 兩者相同
相同的話代表不用刪除,也就是dp[i - 1][j - 1]即為上一次不包含當前兩個數的狀況
- 兩者不相同
不相同的話有三種狀況
- 刪除word1
- 代表不包含當前word1的狀況在加上一個刪除的個數也就是dp[i - 1][j] + 1
- 刪除word2
- 代表不包含當前word2的狀況再加上1個刪除數,也就是dp[i][j - 1] + 1
- 刪除word1、word2
- 代表要不包含word1以及word2的值,也就是dp[i - 1][j - 1] ,並加上刪除兩次,所以是dp[i - 1][j - 1] + 2
- 但也可以想成取word1不存在的部分也就是dp[i - 1][j],並刪除word2,也就是dp[i - 1][j] + 1,反之也可以想成word2不存在。
- 那因為我們要找出最少需要刪除多少次,所以就是取刪除狀況中最小的數值+1
狀態轉移方程就會是 dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + 1;
初始化的部分就是要如何將i - 1結尾的word1以及j - 1結尾的word2 刪除至空字符串,就會需要i, j 次的刪除次數才行。
編輯距離
定義: i - 1 下標的word1以及 j - 1 下標的word2,要達到相同的子序列最少需要操作多少次為dp[i][j]
這一題其實就是前面的部分,只是要想明白相同時要做甚麼、不相同時要做甚麼
如果相同,則不操作
不相同則需要找出最小的增、刪、替換的方案
增加跟刪除可以想成同一個操作數
- 需要增刪word1時,都是取dp[i - 1][j] + 1
- 需要增刪word2時,都是取dp[i][j - 1] + 1
- 至於增刪word1、word2則跟之前一樣,可以簡化成上述的兩個式子
- 需要替換word1或word2的話,則需要取這兩個都不存在的部分加上一次操作數也就是dp[i - 1][j - 1] + 1
所以得出四個轉移方程
if(word1[i - 1] == word2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
總結
在編輯距離的題目當中,有個很重要的核心就是定義好dp[i][j]的定義,在根據這個定義,去推導出公式以及初始化的方式
其實前三題很重要的思維就是對於刪除的理解,在不同的定義上刪除的做法都不太一樣
判斷子序列
刪除是dp[i][j - 1],忽略前一個t
不同子序列
使用s[i - 1]的,我不用刪除任何元素,所以值會是dp[i - 1][j - 1]即上一次的狀況,
如果不使用s[i - 1]的狀況,我等同於只需要不考慮s[i - 1] 但t[j - 1]仍然在,所以值會是dp[i - 1][j]
相同時的轉移方程就會是dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
兩者不相等時相當於s 要刪除元素,因為 s的字符串中,這個位置並沒有t的字串,所以要刪除
如果是s要刪除元素,那就是取s[i - 2] 這個不包含s[ i -1]的最大值,但t是要比較的子序列,所以t不用動,也就是說這個dp[i][j]會是由s[i - 2]t[j - 1]所組成,所對應的dp數組是dp[i][j] = dp[i - 1][j]。
兩個字符串的刪除操作
- 刪除word1
- 代表不包含當前word1的狀況在加上一個刪除的個數也就是dp[i - 1][j] + 1
- 刪除word2
- 代表不包含當前word2的狀況再加上1個刪除數,也就是dp[i][j - 1] + 1
- 刪除word1、word2
- 代表要不包含word1以及word2的值,也就是dp[i - 1][j - 1] ,並加上刪除兩次,所以是dp[i - 1][j - 1] + 2
編輯距離
所謂的增刪基本上是同一個操作數,只是需要明確甚麼是替換,以及下標定義為何
- 需要增刪word1時,都是取dp[i - 1][j] + 1
- 需要增刪word2時,都是取dp[i][j - 1] + 1
- 需要替換word1或word2的話,則需要取這兩個都不存在的部分加上一次操作數也就是dp[i - 1][j - 1] + 1
整體而言編輯距離透過這幾天的理解過後,透過這次的總結,對於這類題目有更深的了解了。
相关文章:
)
代碼隨想錄算法訓練營|第五十八天|583. 两个字符串的删除操作、72. 编辑距离、编辑距离总结篇。刷题心得(c++)
目录 讀題 583. 两个字符串的删除操作 自己看到题目的第一想法 看完代码随想录之后的想法 72. 编辑距离 看完代码随想录之后的想法 583. 两个字符串的删除操作 - 實作 思路 代碼隨想錄思路 Code 72. 编辑距离 - 實作 思路 Code 编辑距离总结篇 判斷子序列 不同…...

JavaScript基础之BOM与DOM
文章目录 BOM操作window对象window的子对象之navigator对象(了解即可)window的子对象之screen对象(了解即可)window的子对象之history对象(了解即可)window的子对象之location对象 弹出框警告框确认框提示框…...
【Linux学习笔记】进程概念(中)
1. 操作系统的进程状态2. Linux操作系统的进程状态3. 僵尸进程4. 孤儿进程5. 进程优先级5.1. 优先级是什么和为什么要有优先级5.2. Linux中的进程优先级 6. 进程切换7. 环境变量7.1. 环境变量的认识7.2. 环境变量相关的命令7.3. 环境变量和本地变量7.4. 命令行参数7.5. 获取环境…...
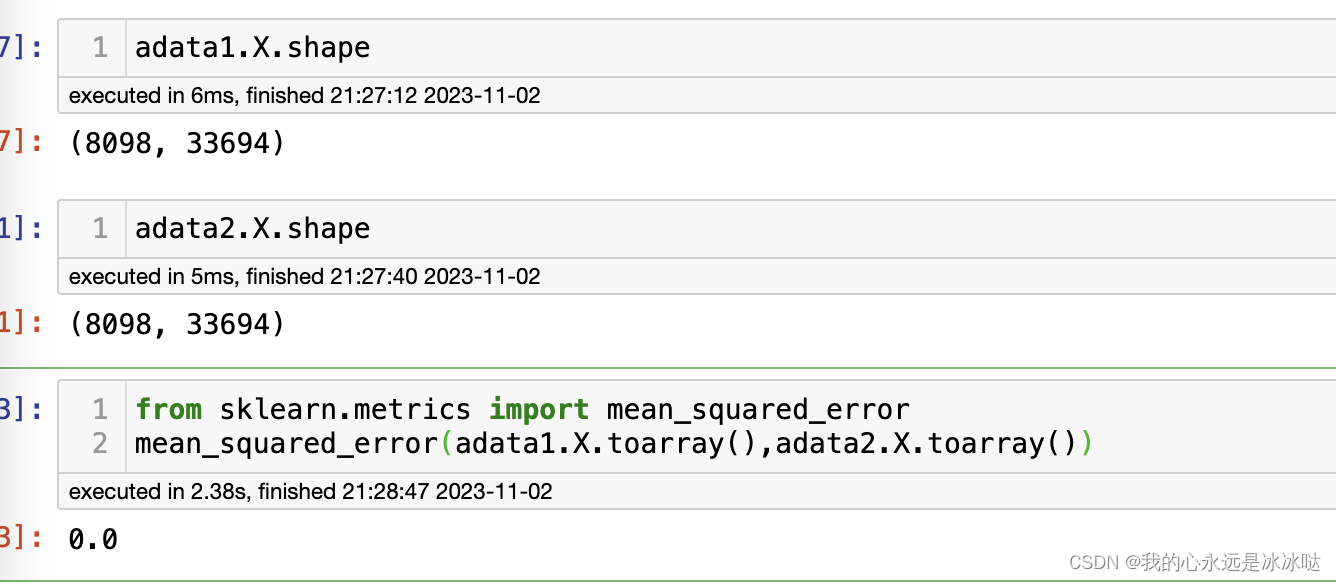
scanpy赋值问题
今天发现一个很奇怪的bug import numpy as np import pandas as pd import anndata as ad from scipy.sparse import csr_matrix print(ad.__version__)counts csr_matrix(np.random.poisson(1, size(100, 2000)), dtypenp.float32) adata1 ad.AnnData(counts) print(adata1)…...
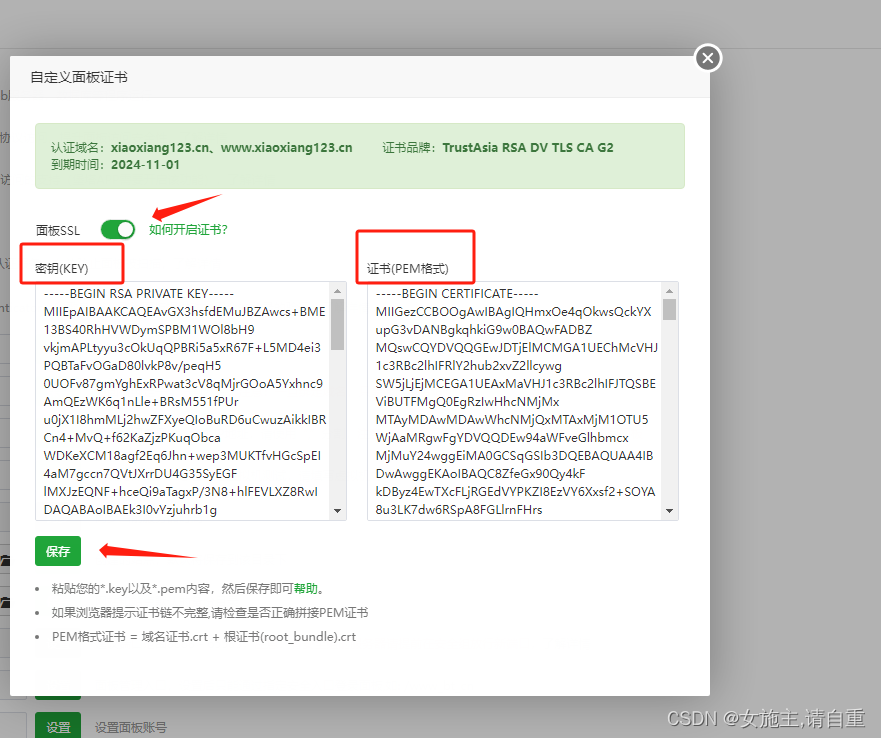
腾讯云域名备案后,如何解析到华为云服务器Linux宝塔面板
一、购买域名并且进行备案和解析,正常情况下,购买完域名,如果找不到去哪备案,可以在腾讯云上搜索“备案”关键词就会出现了,所以这里不做详细介绍,直接进行步骤提示: 二、申请ssl证书࿰…...

odoo 按钮打印pdf报表
odoo打印一般是在动作里面进行的 所以此方法可用自定义按钮进行打印 <template id"report_sale_line_packing_template"> xxx </template><template id"report_sale_line_packing"><t t-call"web.basic_layout"><t …...

用逻辑分析仪观察串口Uart数据波形
一、概述 只讨论嵌入式编程中较为常用的异步串行接口(Universal Asynchronous Receiver/Transmitter, UART),TTL电平。 串口的参数一般有: 1.波特率,数据传输速率,单位bps(bits per…...

数据结构-栈应用括号匹配
1、顺序栈的定义 2、顺序栈的入栈,出栈,取出栈顶元素,匹配判断函数 3、顺序栈的运行测试 4、实现代码 #include<iostream> using namespace std; #define OK 1 #define ERROR 0 #define OVERFLOW -2 typedef int Status; #define M…...

leetcode做题笔记209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。 示例 1: 输入&#…...
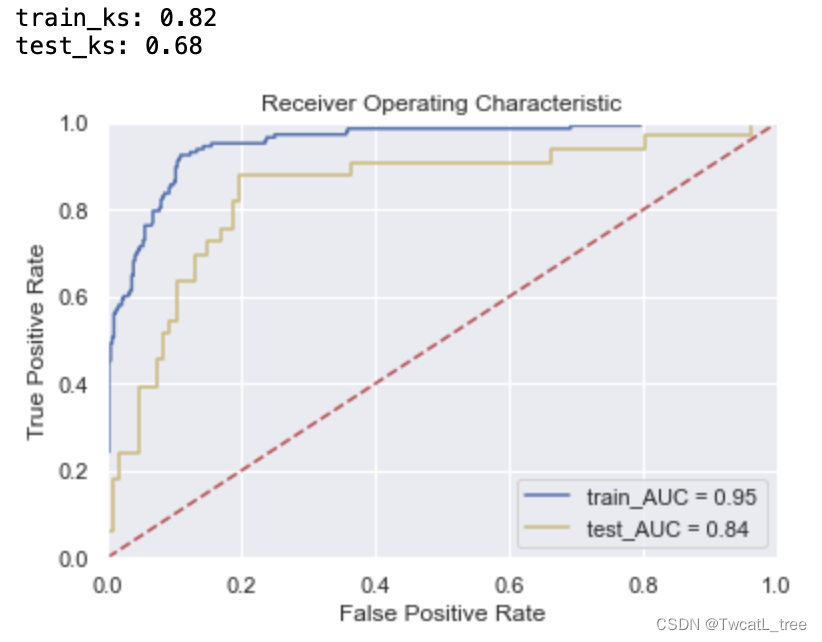
【机器学习】几种常用的机器学习调参方法
在机器学习中,模型的性能往往受到模型的超参数、数据的质量、特征选择等因素影响。其中,模型的超参数调整是模型优化中最重要的环节之一。超参数(Hyperparameters)在机器学习算法中需要人为设定,它们不能直接从训练数据…...

使用免费 FlaskAPI 部署 YOLOv8
目标检测和实例分割是计算机视觉中关键的任务,使计算机能够在图像和视频中识别和定位物体。YOLOv8是一种先进的、实时的目标检测系统,因其速度和准确性而备受欢迎。 Flask是一个轻量级的Python Web框架,简化了Web应用程序的开发。通过结合Fla…...
不使用屏幕在树莓派4B安装Ubuntu22.04桌面版(64位)
因为时间有限只说一下基本路径: 1首先安装Ubuntu22.04server版本 2设置服务器版本的SSH和WiFi 3通过服务器版本安装Ubuntu-desktop升级到Ubuntu22.04桌面版 4在桌面版上安装远程控制软件:xrdp; 5使用Windows自带的远程桌面连接访问Ubuntu 6完成...
Pymysql模块使用操作
一、pymysql模块安装 二、测试数据库连接 测试数据库连接.py from pymysql import Connectioncon None try:# 创建数据库连接con Connection(host"localhost",port3306,user"root",password"XXXXX")# 测试链接print(con.get_host_info())print…...
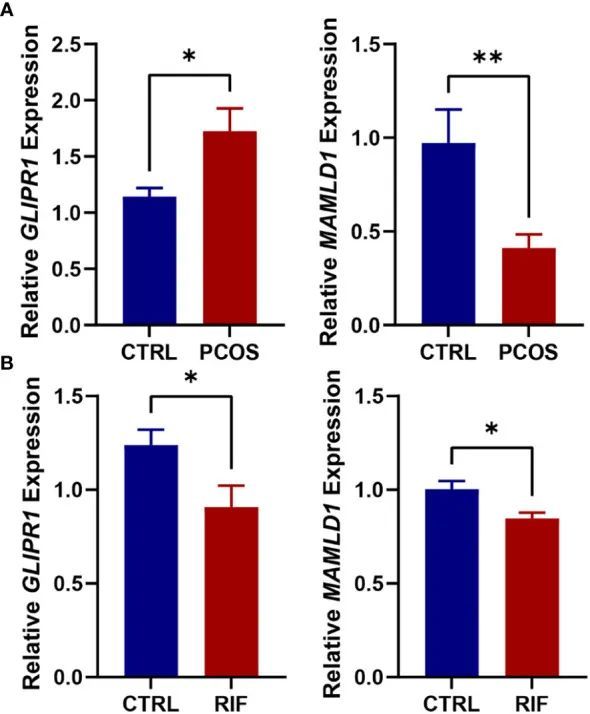
8+双疾病+WGCNA+多机器学习筛选疾病的共同靶点并验证表达
今天给同学们分享一篇双疾病WGCNA多机器学习的生信文章“Shared diagnostic genes and potential mechanism between PCOS and recurrent implantation failure revealed by integrated transcriptomic analysis and machine learning”,这篇文章于2023年5月16日发表…...

springboot如何获取前端请求头的值并加入ThreadLocal
依赖: <dependency><groupId>org.aspectj</groupId><artifactId>aspectjweaver</artifactId><version>1.9.7</version> </dependency>示例: public class ThreadLocalUtil {private static ThreadLoc…...

程序员想要网上接单却看花了眼?那这几个平台你可得收藏好了!
现在经济压力这么大,但是生活成本还在上升,相信大家都知道“四脚吞金兽”的威力了吧!话虽如此,但是生活总得继续,为了家庭的和谐幸福,为了孩子的未来,不少人选择多干几份工作,赚点外…...

前端食堂技术周刊第 102 期:Next.js 14、Yarn 4.0、State of HTML、SEO 从 0 到 1
美味值:🌟🌟🌟🌟🌟 口味:肥牛宽粉 食堂技术周刊仓库地址:https://github.com/Geekhyt/weekly 大家好,我是童欧巴。欢迎来到前端食堂技术周刊,我们先来看下…...
GPT与人类共生:解析AI助手的兴起
随着GPT模型的崭新应用,如百度的1和CSDN的2,以及AI助手的普及,人们开始讨论AI对就业市场和互联网公司的潜在影响。本文将探讨GPT和AI助手的共生关系,以及我们如何使用它们,以及使用的平台和动机。 GPT和AI助手…...
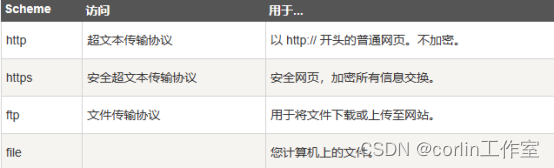
HTML脚本、字符实体、URL
HTML脚本: JavaScript 使 HTML 页面具有更强的动态和交互性。 <script> 标签用于定义客户端脚本,比如 JavaScript。<script> 元素既可包含脚本语句,也可通过 src 属性指向外部脚本文件。 JavaScript 最常用于图片操作、表单验…...

UOS安装Jenkins
一,环境准备 1.安装jdk 直接使用命令行(sudo apt install -y openjdk-11-jdk)安装jdk11 2.安装maven 参考此篇文章即可 UOS安装并配置Maven工具_uos 安装maven_蓝天下的一员的博客-CSDN博客 不过要注意这篇文章有个小错误,我…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
