多线程锁的升级原理是什么
在 Java 中,锁共有 4 种状态,级别从低到高依次为:无状态锁,偏向锁,轻量级锁和重量级锁状态,这几个状态会随着竞争情况逐渐升级。锁可以升级但不能降级。
多线程锁锁升级过程
如下图所示

多线程锁的升级过程主要指的是锁从偏向锁状态升级为轻量级锁状态,再升级为重量级锁状态的过程。以下是多线程锁的升级过程:
1.偏向锁状态
在偏向锁状态下,对象头中的 Mark Word 被设置为偏向锁标记,并记录了持有锁的线程ID。因此,当一个线程访问共享数据时,无需进行同步操作,可以直接进入临界区执行操作。如果其他线程也需要访问该共享数据,此时需要升级为轻量级锁状态。
2.轻量级锁状态
在轻量级锁状态下,对象头中的 Mark Word 被设置为指向锁记录的指针,同时锁记录结构体中包含了持有锁的线程ID和锁标志位等信息。此时,竞争线程会使用CAS(Compare and Swap)操作尝试获取锁,如果成功获取锁,则直接进入临界区执行操作;如果获取失败,则说明存在竞争,需要升级为重量级锁状态。
3.重量级锁状态
在重量级锁状态下,对象头中的 Mark Word 被设置为重量级锁标记,并将当前线程挂起,等待锁被释放后再唤醒线程进行竞争。由于重量级锁采用了操作系统内核的互斥机制,因此会引入较大的性能开销。
在实际应用中,锁的升级过程通常是自动完成的。例如,在偏向锁状态下,当有其他线程竞争同一个锁时,就会自动升级为轻量级锁状态;当竞争激烈时,就会自动升级为重量级锁状态。这种锁升级过程的自动完成是通过对象头中的 Mark Word 标记位来实现的。
在多线程编程中,锁的升级过程是非常重要的,可以根据并发场景进行优化,以提高程序的性能和稳定性。但是,在使用锁的过程中,也要避免死锁等问题,以确保程序的正确性和可靠性。
多线程锁状态对比
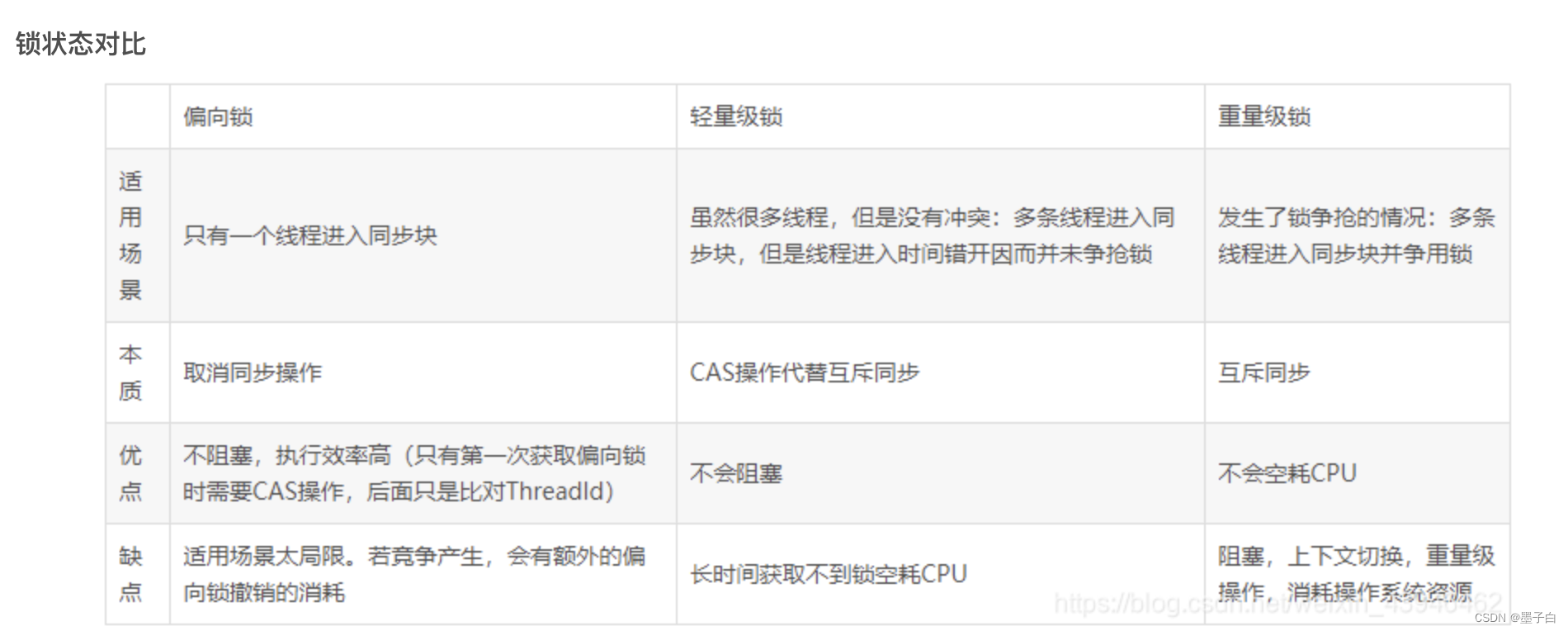
多线程中的锁升级原理
指的是在锁的级别上进行优化,以提高并发性能。Java 中的锁升级机制主要包括无锁、偏向锁、轻量级锁和重量级锁。
-
无锁状态(无同步):当一个线程访问共享数据时,不需要任何同步操作,因为没有其他线程与之竞争。
-
偏向锁状态:当只有一个线程访问共享数据时,该线程会将对象头中标记位设置为偏向锁标记,表示该对象处于偏向锁状态。之后,该线程可以直接进入临界区执行操作,无需进行同步操作。这样,对于只有一个线程访问共享数据的情况,减少了同步的开销。
-
轻量级锁状态:当存在多个线程竞争同一个锁时,对象头中的标记位会变为轻量级锁标记。此时,竞争线程会使用CAS(Compare and Swap)操作来尝试获取锁。如果成功获取锁,则直接进入临界区执行操作;如果获取失败,则说明存在竞争,进一步升级为重量级锁。
-
重量级锁状态:当多个线程竞争同一个锁时,对象头中的标记位会变为重量级锁标记。此时,竞争线程会进入阻塞状态,操作系统会将其挂起,等待锁释放后再唤醒线程进行竞争。
锁的升级原理是为了尽量减少锁带来的性能开销。在程序运行的过程中,锁的状态会根据竞争情况进行升级和降级,以适应不同的并发场景。当只有一个线程访问共享数据时,使用偏向锁可以避免不必要的同步开销;当存在竞争时,使用轻量级锁可以通过CAS操作快速获取锁,避免线程的阻塞和唤醒;当竞争激烈时,使用重量级锁可以确保线程安全,但可能会引入较大的性能开销。
Java 中的锁升级机制是为了在提供线程安全的同时,尽量减少锁带来的性能影响,提高并发性能。
更多消息资讯,请访问昂焱数据(https://www.ayshuju.com/home)
相关文章:

多线程锁的升级原理是什么
在 Java 中,锁共有 4 种状态,级别从低到高依次为:无状态锁,偏向锁,轻量级锁和重量级锁状态,这几个状态会随着竞争情况逐渐升级。锁可以升级但不能降级。 多线程锁锁升级过程 如下图所示 多线程锁的升级过程…...
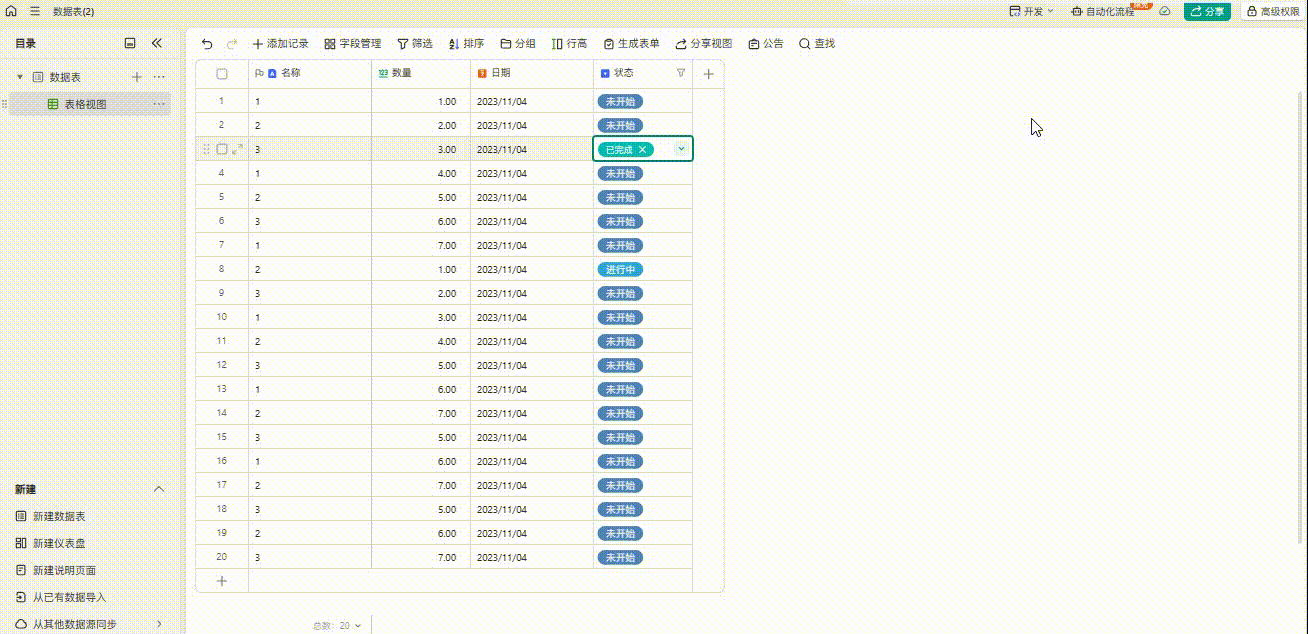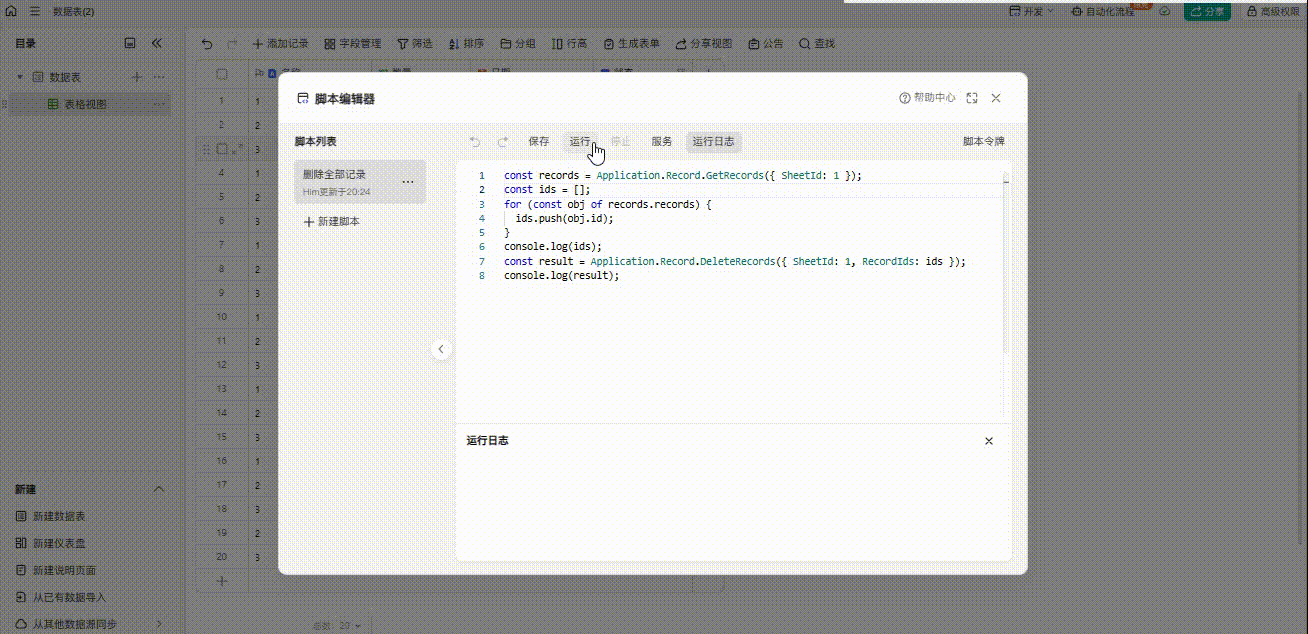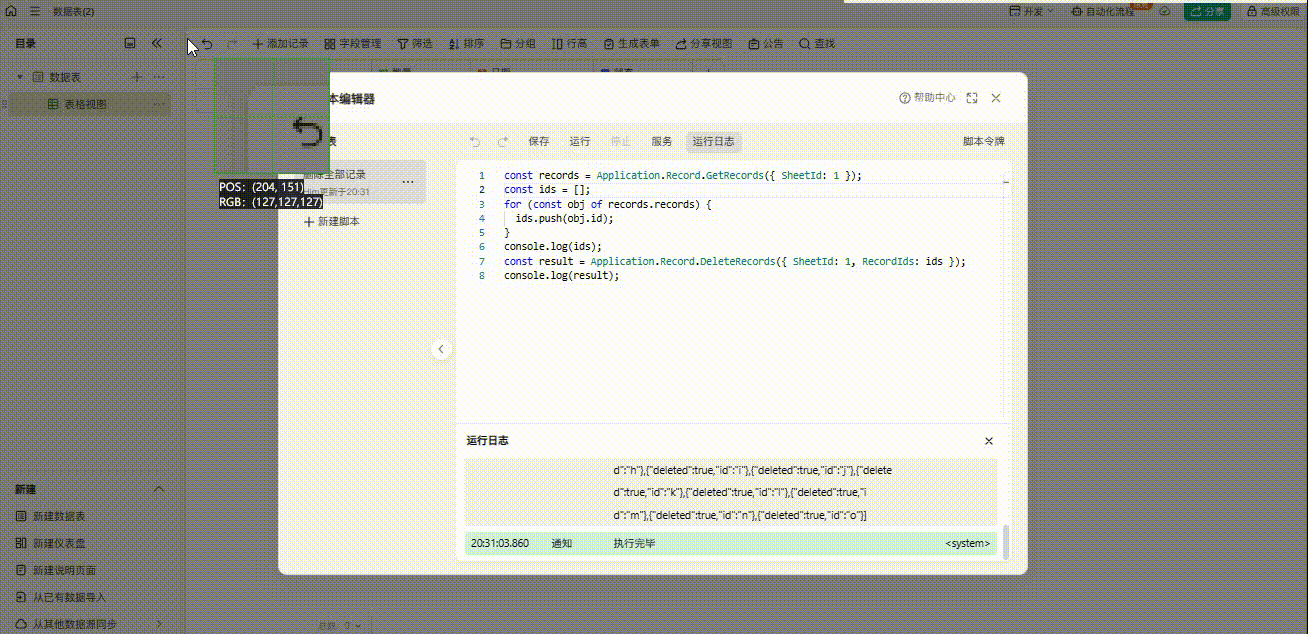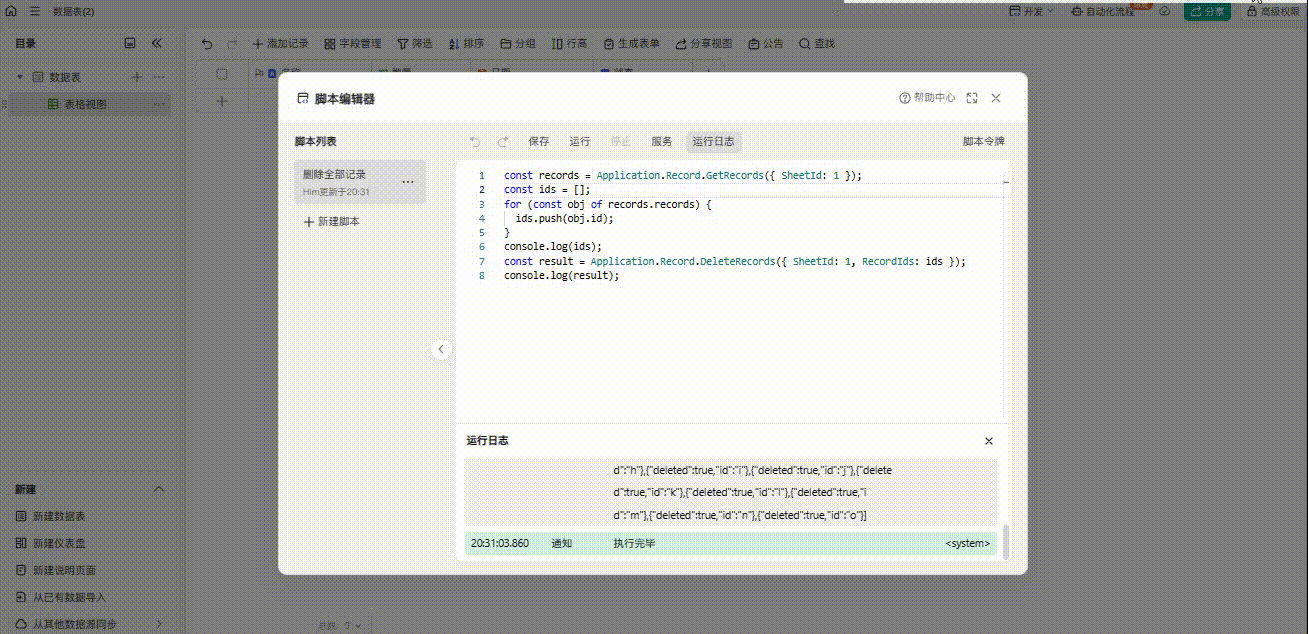
金山文档轻维表之删除所有行记录
目前脚本文档里面的只有删除行记录功能,但是需要指定ID值,不能实现批量删除,很多人反馈但是官方无回应,挺奇怪的 但是批量删除的需求我很需要,最后研究了一下,还是挺容易实现的 测试: 附上脚本…...

站坑站坑站坑站坑站坑
站坑站坑站坑站坑站坑站坑站坑...
语法来动态加载组件)
在Vue中,你可以使用动态import()语法来动态加载组件
在Vue中,你可以使用动态import()语法来动态加载组件。动态导入允许你在需要时异步加载组件,这样可以提高应用程序的初始加载性能。 下面是一个使用动态导入加载组件的示例: <template> <div> <button click"loadComp…...
)
金蝶云星空表单插件获取日期控件判空处理(代码示例)
文章目录 金蝶云星空表单插件获取日期控件判空处理C#实现 金蝶云星空表单插件获取日期控件判空处理 C#实现 DateTime? deliveryDate (DateTime?)this.View.Model.GetValue("FApproveDate");//审核日期long leadtime 20;//天数if (!deliveryDate.IsNullOrEmpty()…...

通过xshell传输文件到服务器
一、user is not in the sudoers file. This incident will be reported. 参考链接: [已解决]user is not in the sudoers file. This incident will be reported.(简单不容易出错的方式)-CSDN博客 简单解释下就是: 0、你的root需要设置好密码 sudo …...

centos7.9编译安装python3.7.2
联网环境下编译安装python3.7.2,不联网则需要配置cnetos7.9离线源 下载解压软件包 [rootlocalhost ~]# tar -xf Python-3.7.3.tar.gz [rootlocalhost ~]# ls anaconda-ks.cfg Python-3.7.3 Python-3.7.3.tar.gz [rootlocalhost ~]# [rootlocalhost ~]# cd Pytho…...

【教3妹学编程-算法题】2913. 子数组不同元素数目的平方和 I
-----------------第二天------------------------ 面试官 : 好的, 我们再来做个算法题吧。平时工作中会尝试用算法吗, 用到了什么数据结构? 3妹 : 有用到, 用到了 bla bla… 面试官 : 好的, 题目是这样的࿱…...

是否会有 GPT-5 的发布?
本心、输入输出、结果 文章目录 是否会有 GPT-5 的发布?前言围绕 GPT-5 的信息OpenAI 期待增长GPT-5 - 到底是真的在训练,还是一个虚构的故事Sam Altman字里行间包含的信息我们在什么时候可以期待 GPT-5 的发布GPT-5 预计将在哪些方向努力GPT-5 在听觉领域GPT-5 在视频处理领…...

使用 Selenium Python 检查元素是否存在
像 Selenium 这样的自动化工具使我们能够通过不同的语言和浏览器自动化 Web 流程并测试应用程序。 Python 是它支持的众多语言之一,并且是一种非常简单的语言。 它的Python客户端帮助我们通过Selenium工具与浏览器连接。 Web 测试对于开发 Web 应用程序至关重要&am…...
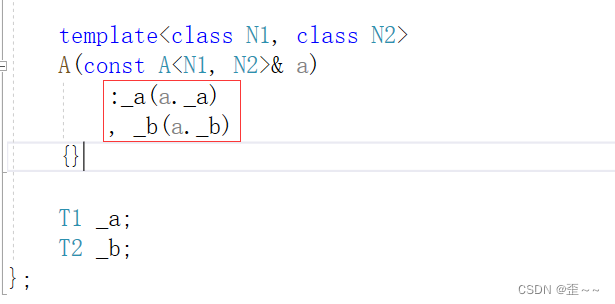
const迭代器与模板构造函数
在自己实现C中list的时候,当实现const迭代器的时候,发现报错了,一直思考到现在 才发现是一个,很简单的问题,但是也让我有了一点感受,我在这里给大家分享一下。文章目录 1.当时遇到的问题2.解决方法3. 自己的…...
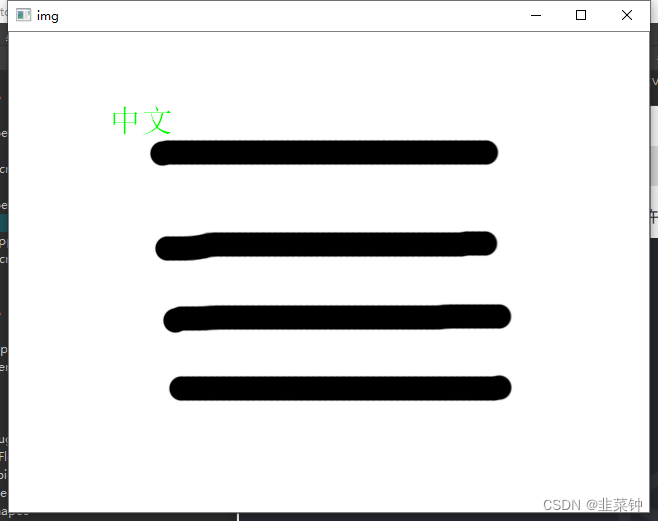
在Qt中解决opencv的putText函数无法绘制中文的一种解决方法
文章目录 1.问题2.查阅资料3.解决办法 1.问题 在opencv中,假如直接使用putText绘制中文,会在图像上出现问号,如下图所示: 2.查阅资料 查了一些资料,说想要解决这个问题,需要用到freetype库或者用opencv…...
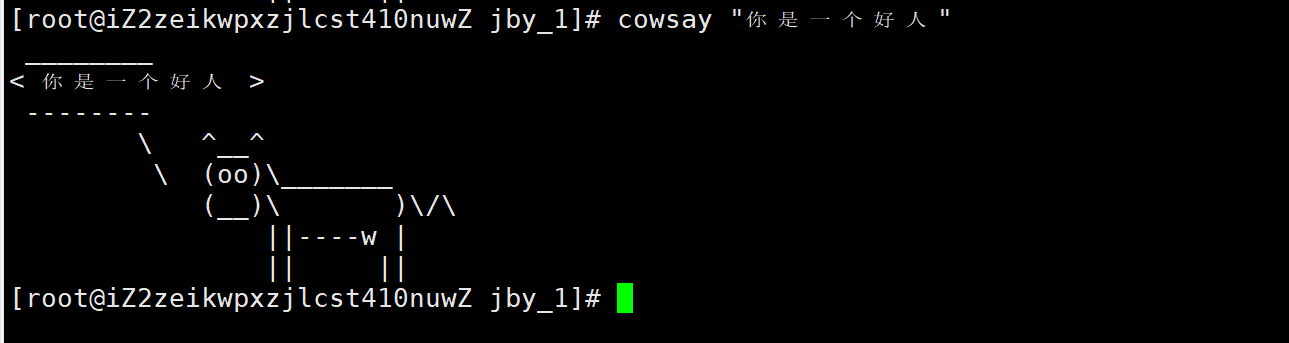
【Linux】第六站:Centos系统如何安装软件?
文章目录 1.Linux安装软件的方式2.Linux的软件生态3. yum4. rzsz软件的安装与卸载5.yum如何知道去哪里下载软件? 1.Linux安装软件的方式 在linux中安装软件常用的有三种方式 源代码安装(我们还需要进行编译运行后才可以,很麻烦) …...
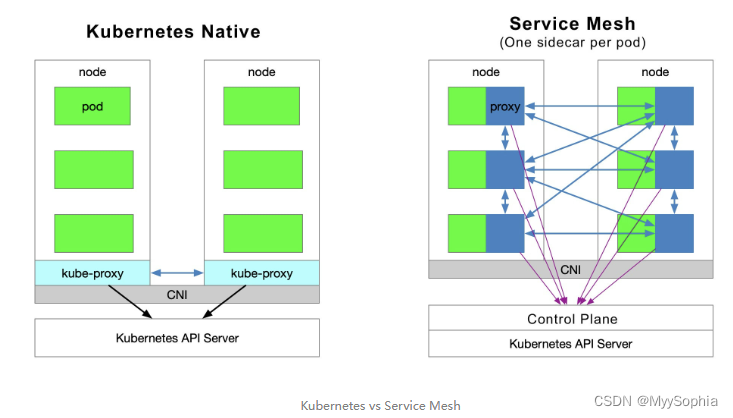
Istio 实战
文章目录 Istio流量管理分享会【1】什么是istio?【2】istio 可以干什么?【3】业务中的痛点?【4】istio 高级流量管理5.1 istio 组件介绍与原理5.2 sidercar何时注入?如何控制是否注入?5.3 查看sidecar 容器插入的容器中的iptablesDestination RuleVirtual ServiceGateways…...

【Midjourney入门教程4】与AI对话,写好prompt的必会方法
文章目录 1、语法2、单词3、要学习prompt 框架4、善用参数(注意版本)5、善用模版6、临摹7、垫图 木匠不会因为电动工具的出现而被淘汰,反而善用工具的木匠,收入更高了。 想要驾驭好Midjourney,可以从以下方面出发调整&…...
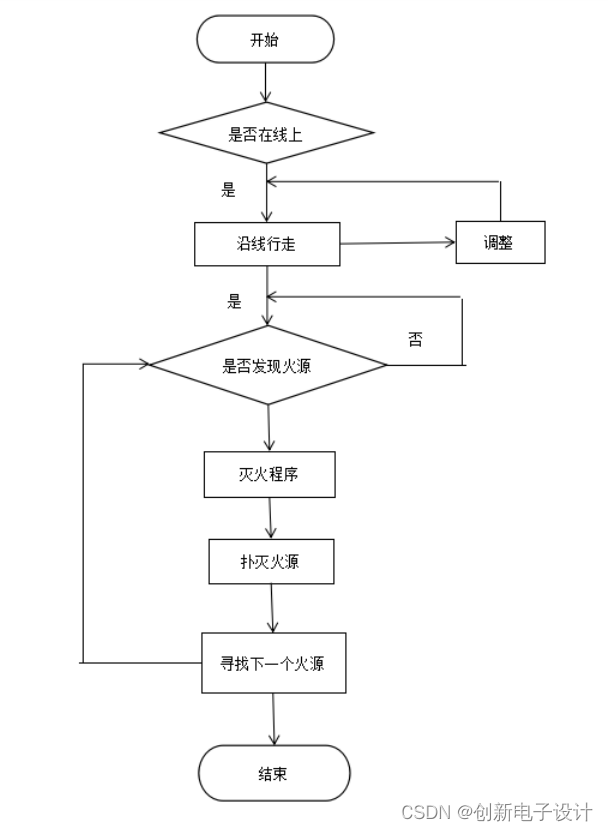
基于单片机的智能灭火小车设计
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 技术交流认准下方 CSDN 官方提供的联系方式 文章目录 概要 一、整体设计方案1.1 整体设计任务1.2 整体设计要求1.3 系统整体方案设计1.3.1 整体模块设计1.3.2 整体设计方案选择…...
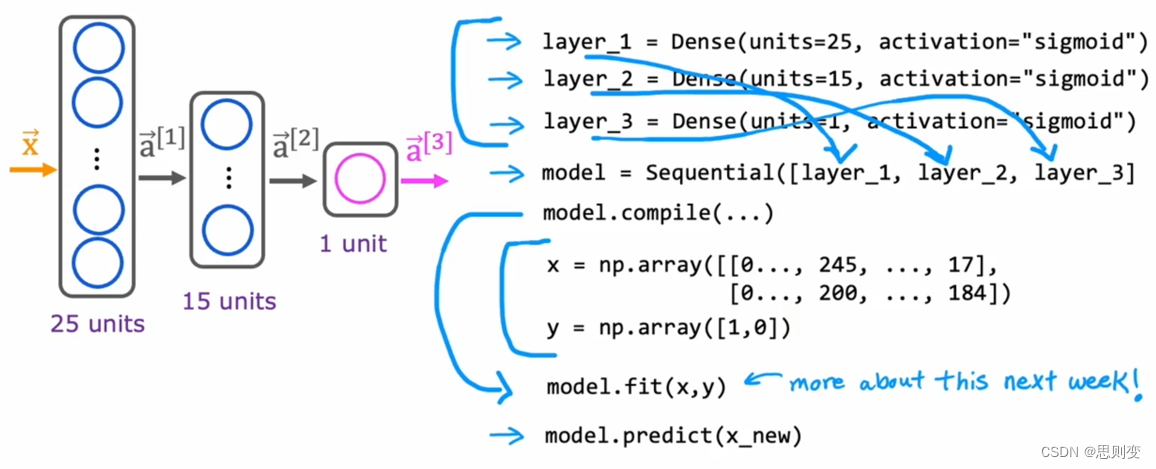
[Machine Learning][Part 7]神经网络的基本组成结构
这里我们将探索神经元/单元和层的内部工作原理。特别是,与之前学习的回归/线性模型和逻辑模型进行比较。最后接介绍tensorflow以及如何利用tensorflow来实现这些模型。 神经网络和大脑的神经元工作原理类似,但是比大脑的工作原理要简单的多。大脑中神经元的工作原理…...

精准测试:提高软件质量和用户满意度的利器
📢专注于分享软件测试干货内容,欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢交流讨论:欢迎加入我们一起学习!📢资源分享:耗时200小时精选的「软件测试」资…...
)
代碼隨想錄算法訓練營|第五十八天|583. 两个字符串的删除操作、72. 编辑距离、编辑距离总结篇。刷题心得(c++)
目录 讀題 583. 两个字符串的删除操作 自己看到题目的第一想法 看完代码随想录之后的想法 72. 编辑距离 看完代码随想录之后的想法 583. 两个字符串的删除操作 - 實作 思路 代碼隨想錄思路 Code 72. 编辑距离 - 實作 思路 Code 编辑距离总结篇 判斷子序列 不同…...

JavaScript基础之BOM与DOM
文章目录 BOM操作window对象window的子对象之navigator对象(了解即可)window的子对象之screen对象(了解即可)window的子对象之history对象(了解即可)window的子对象之location对象 弹出框警告框确认框提示框…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
