代码随想录算法训练营第四十二天 | LeetCode 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零
代码随想录算法训练营第四十二天 | LeetCode 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零
文章链接:最后一块石头的重量 II 目标和 一和零
视频链接:最后一块石头的重量 II 目标和 一和零
1. LeetCode 1049. 最后一块石头的重量 II
1.1 思路
- 这题不要被题目的示例给带偏,其实就是看看我们能不能把石头尽量分成两堆,比如示例的总和为 23,看看能不能分成一半就是 11,另一半就是 12 了,一相撞就是剩下 1 了。即尽量分成重量总和近似相等的两堆,就是想到本题的关键了,这么看和416. 分割等和子集还是很像的,区别就是那题是能分成子集相等的就是 true 反之 false,本题是尽量凑,凑不成就相撞所剩下的重量也是最小的。
- dp 数组的下标及其含义:在 01 背包中,背包容量为 j 所能带的最大价值为 dp[j]。但本题的重量/容量也是它的价值,所以这里的最大价值也是它的最大重量,背包容量为 j 所能带的最大重量为 dp[j]
- 递推公式:在 01 背包中,dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i]),前者是不放物品 i,后者是放物品 i。在本题中 dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]),前者是不放石头 i,后者是放石头 i
- dp 数组的初始化:dp[0]=0,容量 0 的背包能放的重量也是 0。其他下标初始化为 0,因为我们的递推公式是通过别的值覆盖 dp[j] 的,因此不能初始化太大,为 0 最正确。我们这里定义 dp 数组的大小就是,先求 sum,target=sum/2,dp 数组的大小就是 target+1,因为我们要凑容量的一半
- 遍历顺序:两层 for循环,for(int i=0;i<stones.length;i++)for(int j=target;j>=stones[i];j–)先物品后背包,然后背包这一层从后往前遍历,这里为什么j>=stones[i] 是因为如果背包容量比石头重量还小再遍历就没有意义了
- 打印 dp 数组:用于 debug
- 最后 return sum-2*dp[target]
1.2 代码
class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0;for (int i : stones) {sum += i;}int target = sum >> 1;//初始化dp数组int[] dp = new int[target + 1];for (int i = 0; i < stones.length; i++) {//采用倒序for (int j = target; j >= stones[i]; j--) {//两种情况,要么放,要么不放dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
}
2. LeetCode 494. 目标和
2.1 思路
- 我们可以在集合中加入“+”“-”变为一个表达式,使其等于我们的 target。关于放“+”还是“-”就是把这个集合分成了两个集合,放加法的是一个集合,放减法的是一个集合。本题和416. 分割等和子集也是一个集合里分两个子集还有1049. 最后一块石头的重量 II也是一个集合里分出两个子集。本题中我们加法用 left,减法用 right,加法和减法的集合就是原集合的总和 sum,要求加法集合 left-减法集合 right=target,一相加就是 2left=sum+target => 即 left=(sum+target)/2。举例 [1,1,1,1,1] 即 sum=5,题目的 target=3,因此 left=(5+3)/2,就是 4 个用加法,1 个用减法,我们求出 left 集合剩下的就是 right 集合了。当然也是有用例是求不出 left 集合的,比如如果上面的是 target=2,那我们的 left 和 right 都找不到一种匹配的集合等于 target,因此如果判断出 (target+sum)%2!=0 就最终输出 0。此时问题转化为,求出 left 集合,原集合里所有元素装满这个 left 集合有多少种方法,就能找到符合题目条件的多少种组合,这就是背包问题了,left 就是背包容量,原集合就是我们的物品
- 纯 01 背包就是问装满这个背包的最大价值,416. 分割等和子集就是能不能装满这个背包,满了就 true 否则就 false,1049. 最后一块石头的重量 II结束尽量去装,能装多少装多少,本题就是给我们一个容量,问有多少种方式能把背包装满
- dp 数组及其下标的含义:dp[j] 装满背包容量为 j 有 dp[j] 种方法。bagSize=(target+sum)/2
- 递推公式:dp[j]+=dp[j-nums[i]]

- dp 数组的初始化:在 01 背包中 dp[0] 初始化为 0,即背包容量为 0 的背包最大价值是 0,但是本题,dp[0] 应该初始化为 1,因为我们的 dp[j] 是通过前面累加的,如果初始化为 0,后面就一直是 0 了
- 遍历顺序:01 背包中先物品再背包,因此 for(int i=0;i<nums.length;i++)for(int j=bagSize;j>=nums[i];j–)第二层倒序遍历,然后 dp[j]+=dp[j-nums[i]]
- 打印 dp 数组:用于 debug
2.2 代码
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int i = 0; i < nums.length; i++) sum += nums[i];//如果target过大 sum将无法满足if ( target < 0 && sum < -target) return 0;if ((target + sum) % 2 != 0) return 0;int size = (target + sum) / 2;if(size < 0) size = -size;int[] dp = new int[size + 1];dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = size; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[size];}
}
3. LeetCode 474. 一和零
3.1 思路
- 本题让我们从题目的集合中找出一个最多元素的子集,满足有 m 个 0,n 个 1。可以把 m 个 0 和 n 个 1 理解为一个背包,有两个维度,最多有 m 个 0 和 n 个 1,而集合里的元素就是物品。但这题不是多重背包,还是 01 背包,每个物品只能是使用 1 次,只是有两个维度。而多重背包是会限制物品的个数。
- 纯 01 背包就是问装满这个背包的最大价值,416. 分割等和子集就是能不能装满这个背包,满了就 true 否则就 false,1049. 最后一块石头的重量 II结束尽量去装,能装多少装多少,494. 目标和就是给我们一个容量,问有多少种方式能把背包装满,本题是求装满这个背包最多有多少个物品
- dp 数组及其下标的含义:我们是要装满一个 m 个 0、n 个 1 这么大容器的背包,这个背包里最多有多少个物品,一共 3 个变量,m、n、多少个物品。两个维度 m 个 0、n 个 1,因此定义个二维 dp 数组,含义是最多有 i 个 0 j 个 1 的 strs 的最多有 dp[i][j] 个物品,最终 dp[m][n] 就是我们的结果
- 递推公式:纯 01 背包的公式是 dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i]),本题中我们物品的重量就是 x 个 0 y 个 1,整个背包最大重量是 m 个 0 n 个 1。因此 dp[i-x][j-y]+1,这里减去的 x 和 y 就是物品的重量,+1 就是物品的价值,价值就是个数,我们求的就是最多个数。可以这么理解:放了物品 i,还剩下 j - weight[i] 的容量可以放其他物品,剩下空间能得到的最大价值是 dp[i-1][j-weight[i]] 这句话是引用 01 背包理论基础的,理解一下。因此 dp[i][j]=Math.max(dp[i][j], dp[i-x][j-y]+1)
- dp 数组的初始化:dp[0][0]=0,背包容量为 0 了,最大的物品个数自然也是 0。非 0 下标 dp[i][j] 物品个数不会是负数,因此初始化为 0,就不会在递推时 dp[i][j] 被初始化值覆盖掉
- 遍历顺序:也是"两层"for循环,先物品再背包。先通过增强 for循环遍历 str,每遍历到一个物品就要用 x 和 y 记录有几个 0 和 1。然后就是遍历背包,这里是要遍历 0 和 1,我们是先 0 再 1,不过可以颠倒,但是要倒序遍历, for(int i=m;i>=x;i–)for(int j=n;j>=y;j–)
- 打印 dp 数组:用于 debug
3.2 代码
class Solution {public int findMaxForm(String[] strs, int m, int n) {//dp[i][j]表示i个0和j个1时的最大子集int[][] dp = new int[m + 1][n + 1];int oneNum, zeroNum;for (String str : strs) {oneNum = 0;zeroNum = 0;for (char ch : str.toCharArray()) {if (ch == '0') {zeroNum++;} else {oneNum++;}}//倒序遍历for (int i = m; i >= zeroNum; i--) {for (int j = n; j >= oneNum; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
}
相关文章:

代码随想录算法训练营第四十二天 | LeetCode 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零
代码随想录算法训练营第四十二天 | LeetCode 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零 文章链接:最后一块石头的重量 II 目标和 一和零 视频链接:最后一块石头的重量 II 目标和 一和零 1. LeetCode 1049. 最后一块石头的重量 II 1.1 思路…...

Windows PowerShell 和 Linux BashShell 极简对比
声明:本文不会涉及原理,详细的介绍,也不是入门文章。仅仅从使用上进行简单比较 命令 在 bash 中,一个命令是一个单独的进程;而在 PowerShell 中,命令被称为 cmdlets,他们不是独立的可执行程序&…...

校验验证码是否过期(定时刷新验证码)
需求: 我们在登录的时候会遇到通过接口请求验证码的操作,这里的验证码会有过期的时间,当我们验证码过期了,我们要进行重新刷新验证码。 我们这里根据后端返回的当前时间和过期时间判断,过期的时间超过了当前时间的时候…...

windows idea本地执行spark sql避坑
本地安装了IDEA,并配置好了相关POM,可以在本机使用sparkSession连接数据,并在数据库执行sql,在idea展示执行结果。 但是,如果将数据的查询结果建立到spark中,再展示,就会报错 Error while run…...
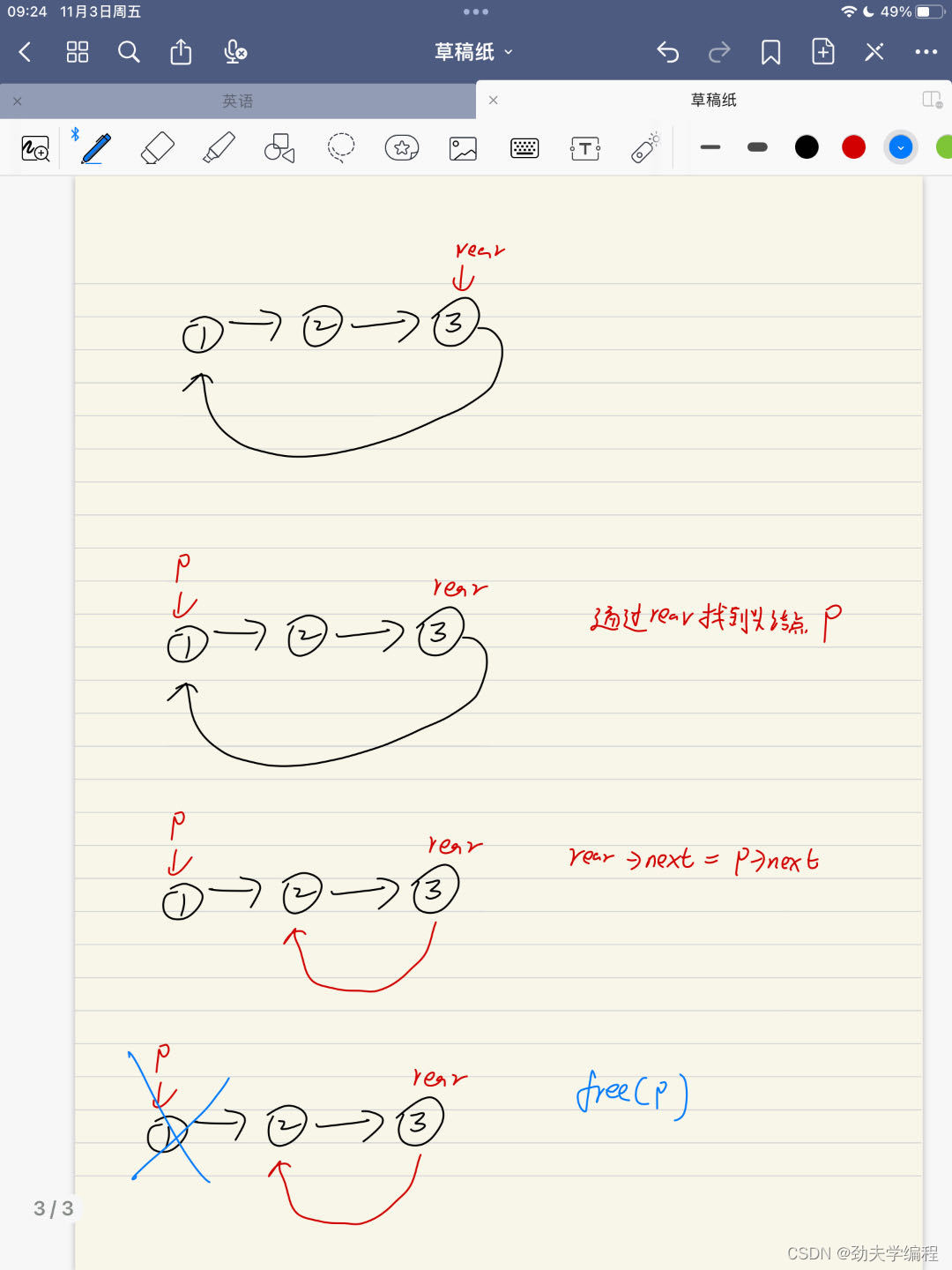
在一个循环链队中只有尾指针(记为rear,结点结构为数据域data,指针域next),请给出这种队列的入队和出队操作实现过程
在一个循环链队中只有尾指针(记为rear,结点结构为数据域data,指针域next),请给出这种队列的入队和出队操作实现过程 入队过程如下图: 先创一个结点,用于存储要插入的结点数据 然后就是老套路了…...

智能客服系统应用什么技术?
随着科技的飞速发展,智能客服系统逐渐出现在我们的生活中。这些系统不仅能够提供即时的客户服务,还可以通过人工智能等技术实现更加高效和准确的服务。那么,智能客服系统究竟应用了哪些技术呢?本文将详细解析。 1、机器学习技术 …...

亚马逊、美客多卖家测评:如何建立养号团队实现运营化式测评?
大家好,我是跨境电商测评养号7年从事经验的珑哥。养号环境软件开发,深度解决各跨境平台矩阵养号防关联、砍单、F号问题。关注珑哥解决更多跨境养号测评问题。 测评,相信这个词对于大部分跨境卖家来说,想必都不陌生,因…...

苹果IOS系统webglcontextlost问题-解决方案
问题描述 在IOS手机 解码视频流的时候,第一次可以正常播放,但只要IOS手机熄屏,再重新唤醒,就会一直播放失败,无论换哪个浏览器都不行。安卓手机则一切正常。 经过排查,发现 IOS手机 的浏览器会无故 webGL…...

供应链ERP之合同:创建、修订与模板
本人详解 作者:王文峰,参加过 CSDN 2020年度博客之星,《Java王大师王天师》 公众号:JAVA开发王大师,专注于天道酬勤的 Java 开发问题中国国学、传统文化和代码爱好者的程序人生,期待你的关注和支持!本人外号:神秘小峯 山峯 转载说明:务必注明来源(注明:作者:王文峰…...
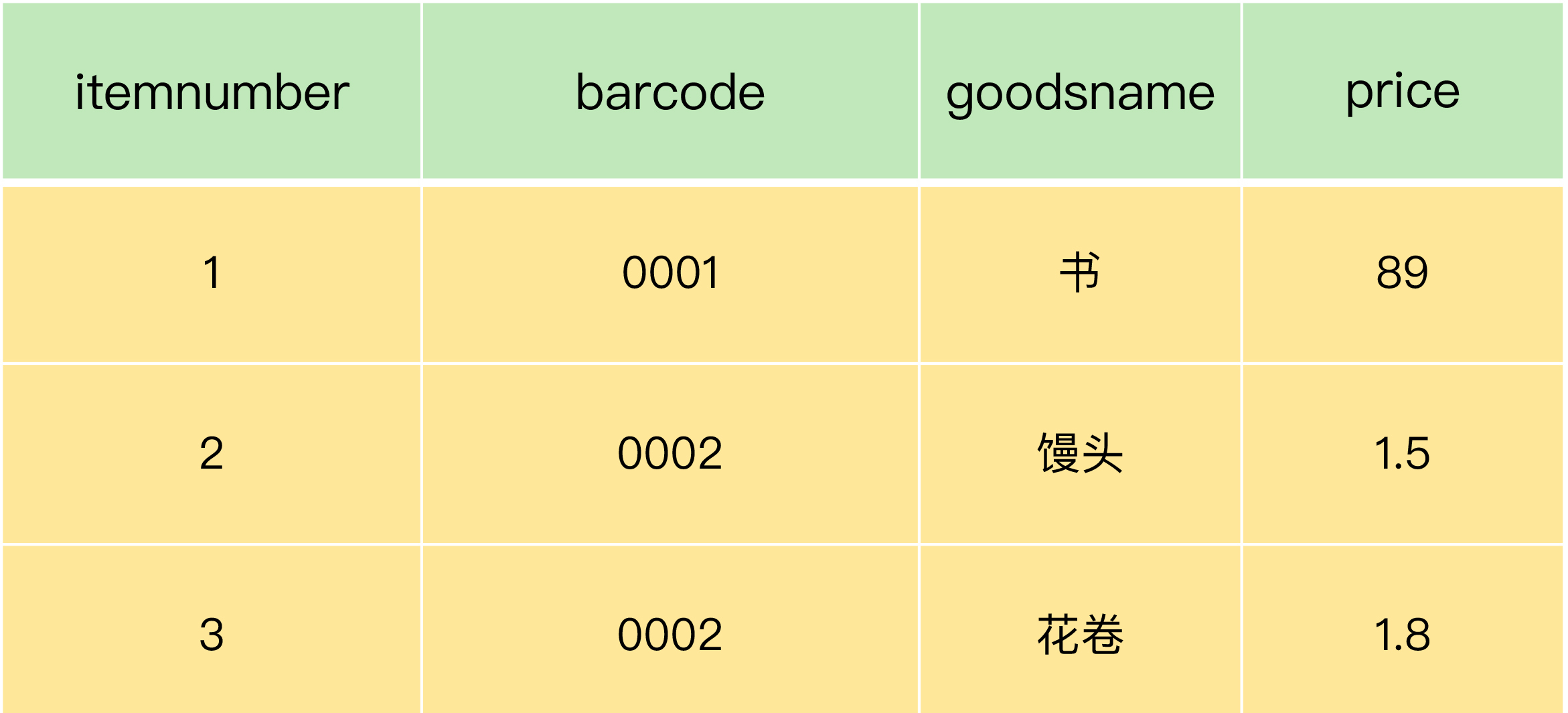
MySQL第二讲·表的创建与修改
你好,我是安然无虞。 文章目录 表:怎么创建和修改数据表?1. 如何创建数据表?2. 都有哪些约束?3. 如何修改表?添加字段修改字段 表:怎么创建和修改数据表? 创建和修改数据表&#x…...

springboot的循环依赖问题描述及解决方案
一.了解循环依赖的场景 在Spring Boot中,循环依赖是指两个或多个Bean之间相互依赖,导致它们无法正确地创建和注入。循环依赖可能会导致应用程序无法启动或出现其他异常。 在以下情况下,您可能需要显式设置循环依赖: 两个Bean相…...

当科技遇上神器:用Streamlit定制AI可视化问答界面
Streamlit是一个开源的Python库,利用Streamlit可以快速构建机器学习应用的用户界面。 本文主要探讨如何使用Streamlit构建大模型外部知识检索的AI问答可视化界面。 我们先构建了外部知识检索接口,然后让大模型根据检索返回的结果作为上下文来回答问题。…...

毛泽东思想和中国特色社会主义理论概论平时作业四
毛泽东思想和中国特色社会主义理论概论平时作业四 1.单选题 1.1人民代表大会制度是中国人民当家作主的基本政治制度,是我国的国体。(b) a.正确 b.错误 人民代表大会制度是中国人民当家作主的根本政治制度,是我国的政体。1.2我国的政体是人民民主专政。…...
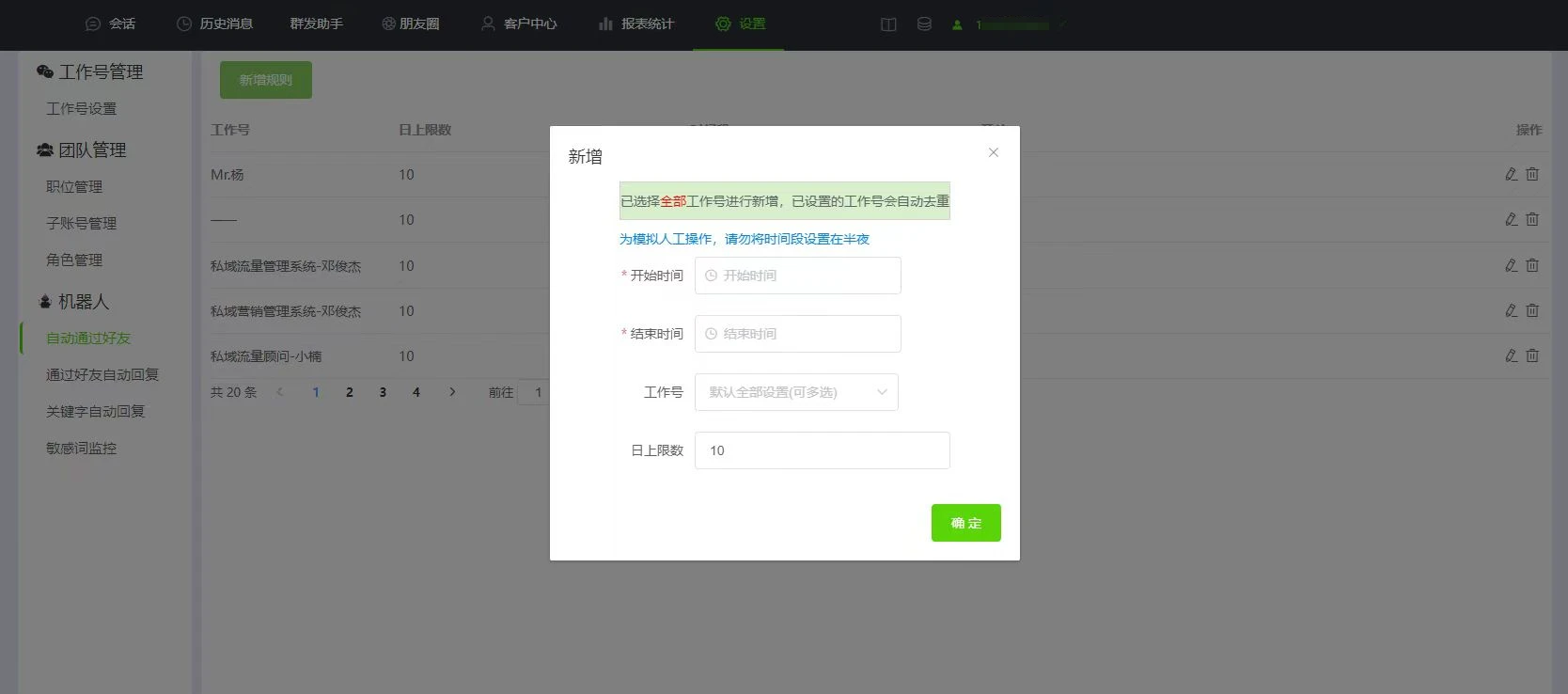
微信怎么设置自动通过好友申请?
当开展引流获客活动时,员工会在一段时间内频繁收到好友添加的申请,手动同意好友请求费时费力还容易出现漏加的情况,那么微信能自动通过好友请求吗? 如何设置快速自动通过好友申请呢? 当微信号在系统登录,…...
)
亲测解决Pytorch TypeError: object of type ‘numpy.int64‘ has no len()
这个问题是小虎在初始化自适应平均池化的时候遇到的,解决方法是限制初始化时池化大小的类型。 问题原文 Exception has occurred: TypeError object of type numpy.int64 has no len()File "D:\Complier\LEF\lib\model\segmentation\heads\modules\fgModules…...

前端模拟实现可编辑的表格table插件
在做项目中遇到了一个供货记录的功能,要求用户自己编辑添加删除表格数据,接下来我们就模拟下前端如何实现该功能 <!DOCTYPE html> <html lang"zh"><head><meta charset"UTF-8"><meta http-equiv"X-…...

PerfectPixel 插件,前端页面显示优化工具
1.简介 PerfectPixel 插件是一款适用于 Chrome 浏览器的网页前端页面显示优化工具,该插件能够帮助开发人员和标记设计人员在开发时将设计图直接加载至网页中,与已成型的网页进行重叠对比,以规范网页像素精度 作为一款可以优化前端页面显示的…...
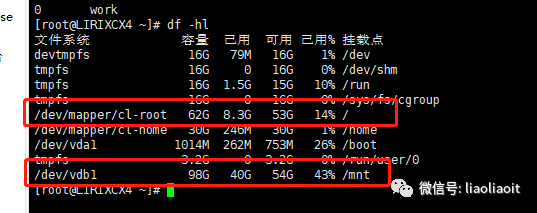
mysql迁移data目录(Linux-Centos)
随着时间的推移,mysql的数据量越越大,使用yum默认安装的目录为系统盘 /var/lib/mysql,现重新挂载了一个硬盘,需要做数据目录的迁移到 /mnt/data/。以解决占用系统盘过高情况。 1.强烈建议这种操作。镜像一个一样的Centos系统&…...

linux-等保测评
#查看审计规则 #auditctl -l #添加审计规则 #auditctl -w /etc/passwd -p rwxa(注意:用 auditd 添加审计规则是临时的,立即生效,但是系统重启失效。) #-w path : 指定要监控的路径,上面的命令指定了监控的文…...

一、React基础知识
一、环境安装 第一种:使用原生搭建(可以从国内下载配置镜像、也可以从国外下载) 指令:1.国内下载:(1:npm config set registry https://r.npm.taobao.org// (2:npm install -g create-react-app…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
