【排序算法】 计数排序(非比较排序)详解!了解哈希思想!

文章目录
- 📑前言
- 🌤️计数排序的概念
- ☁️什么是计数排序?
- ☁️计数排序思想
- ⭐绝对映射
- ⭐相对映射
- 🌤️计数排序的实现
- ☁️实现思路
- ☁️代码实现
- ☁️代码解析
- 🌤️计数排序特性总结
- ☁️时间复杂度:
- ☁️空间复杂度
- ☁️稳定性
- ☁️适用性限制
- ☁️不适用于大规模数据
- ☁️总结
- 🌤️全篇总结
📑前言
什么是计数排序?计数排序的思想是什么?它是如何实现的?
本文会对计数排序进行由浅入深的探究,让你彻底掌握计数排序!
🌤️计数排序的概念
☁️什么是计数排序?
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。
统计每个元素出现的次数,然后根据元素的大小顺序将它们放入正确的位置。
☁️计数排序思想
计数排序是一种小众的排序,它适合于数据密集的场景,按最大数的数值来开空间。
⭐绝对映射
假设现有一组数据,最大的数据是1000,那么便会开一千个大小的空间,这种属于绝对映射,在极端的场景下,极易造成空间上的浪费,比如现在有5,99,88,1000,8888,452,635,82,777,555,只有10个数但是最大的数是8888因此要开8888大小的空间,剩余的空间全部都浪费了。
⭐相对映射
因此绝大多数情况下,都会使用相对映射。
具体的步骤如下:
- 找出待排序数组中的最大值和最小值,并创建一个计数数组,长度为最大值和最小值之差加1。
- 遍历待排序数组,统计每个元素出现的次数,并将次数存储在计数数组的相应位置上。
- 对计数数组进行累加操作,得到每个元素在排序后数组中的最终位置。
- 创建一个与待排序数组长度相同的临时数组,用于存储排序后的结果。
- 从后向前遍历待排序数组,根据计数数组中每个元素的值,将元素放入临时数组的相应位置上。
- 将临时数组中的元素复制回待排序数组,完成排序。

🌤️计数排序的实现
☁️实现思路
- 找到数组中的最小值和最大值,以确定计数数组的大小。
- 然后,根据最小值和最大值计算计数数组的大小,并分配内存空间。
- 接下来,将计数数组的所有元素初始化为0。
- 然后,遍历原数组,统计每个元素出现的次数,将统计结果保存在计数数组中。
- 接着,使用两个循环,将计数数组中的元素按照次数依次放回原数组中。
- 最后,释放计数数组的内存空间。
☁️代码实现
//计数排序
void CountSort(int* a, int n)
{int min = a[0];int max = a[0];for (int i = 0; i < n; i++){if (a[i] < min){min = a[i];}if (a[i] > max){max = a[i];}}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail");exit(-1);}memset(count, 0, sizeof(int) * range);for (int i = 0; i < n; i++){count[a[i] - min]++;}int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}
☁️代码解析
- 寻找最小值和最大值: 首先,通过循环遍历输入数组
a,找到数组中的最小值min和最大值max。这是为了确定排序范围。 - 确定排序范围: 计算排序范围
range,即(max - min + 1),这表示需要排序的整数范围。 - 创建计数数组: 使用
malloc函数为计数数组count分配内存,该数组的大小是排序范围range。计数数组用于存储每个整数在输入数组中出现的次数。 - 初始化计数数组: 使用
memset函数将计数数组count中的所有元素初始化为0。 - 计数: 遍历输入数组
a,对于每个整数a[i],将其减去min的值作为索引,然后在计数数组中对应索引位置的值加1。这一步会统计每个整数在输入数组中出现的次数。 - 重构排序数组: 使用两个循环,首先遍历计数数组
count,然后在内部循环中,根据计数数组中的值,将相应数量的整数值还原到原始输入数组a。这将完成排序过程。
🌤️计数排序特性总结
☁️时间复杂度:
计数排序的时间复杂度为 O(n+k),其中 n 是输入数组的大小,k 是整数的范围。它具有线性时间复杂度的优点,适用于整数排序,特别是当整数范围相对较小且分布均匀时。
☁️空间复杂度
计数排序的空间复杂度取决于整数范围,为 O(k)。因此,它需要额外的空间来存储计数数组,当整数范围较大时可能会占用较多内存。
☁️稳定性
计数排序是一种稳定的排序算法。稳定性意味着具有相同值的元素在排序后仍保持相对顺序不变。在计数排序中,具有相同值的元素会按照它们在输入数组中的顺序被放置在输出数组中。
☁️适用性限制
计数排序仅适用于整数排序,特别是当整数范围相对较小且分布均匀时。它不适用于排序包含负数或浮点数的数组。此外,如果整数范围过大,可能会导致内存占用过多。
☁️不适用于大规模数据
尽管计数排序具有线性时间复杂度的优点,但它对于大规模数据集的排序可能并不理想。当整数范围非常大且分布不均匀时,计数排序的性能可能会受到限制。
☁️总结
计数排序适用于特定范围内的整数排序,并且在这种情况下具有稳定的性能表现。然而,在应用计数排序时,需要仔细考虑整数范围和数据集的分布情况,以确保不会出现内存占用过大或性能下降的情况。
🌤️全篇总结
本章专门对计数排序从概念到实现,进行了细致入微的讲解,期望对你理解掌握计数有所帮助!
看到这里希望给博主留个:👍点赞🌟收藏⭐️关注!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。

相关文章:

【排序算法】 计数排序(非比较排序)详解!了解哈希思想!
🎥 屿小夏 : 个人主页 🔥个人专栏 : 算法—排序篇 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言🌤️计数排序的概念☁️什么是计数排序?☁️计数排序思想⭐绝对…...
20231103配置cv180zb的编译环境【填坑篇】
20231103配置cv180zb的编译环境【填坑篇】 2023/11/3 11:36 感谢您选择了晶视科技的cv180zb,让我们一起来填坑。 在你根据文档找不到答案的时候,是不是想把他们家那个写文档的家伙打一顿,我顶你。 当你在在网上找一圈,BAIDU/BING/…...
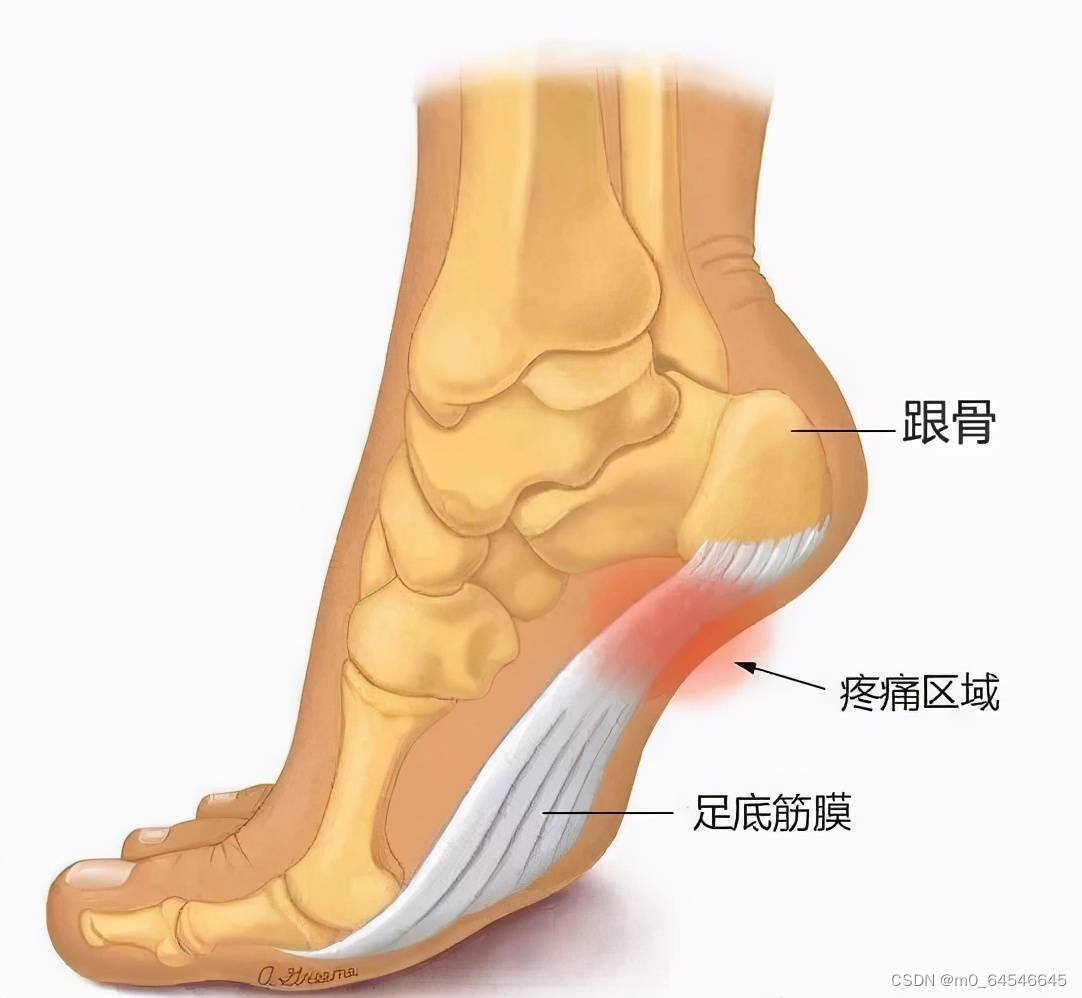
足底筋膜炎如何治疗
足底筋膜炎主要表现为下床站立后或休息后再次走路时,出现足跟部的疼痛与不适症状,活动后可自行缓解,但走路时间长或较剧烈活动后,疼痛会再次加重,甚至有针扎样疼痛感向脚前部发散,影响患者的日常生活。 足…...

rabbitMq路由键介绍
rabbitTemplate.convertAndSend() 是 Spring AMQP 中用于发送消息到 RabbitMQ 的方法。下面是对您提供的代码示例的解释: rabbitTemplate.convertAndSend("ums-platform.ex", "ums.report.routing", param);这行代码主要完成以下几个操作&…...

【python基础】python切片—如何理解[-1:],[:-1],[::-1]的用法
文章目录 前言一、基本语法二、切片1.a[i:j]2.a[i:j:k] 总结:[-1] [:-1] [::-1] [n::-1] 前言 在python中,序列是python最基本的数据结构,包括有string,list,tuple等数据类型,切片对序列型对象的一种索引方…...

剑指JUC原理-9.Java无锁模型
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码🔥如果感觉博主的文章还不错的话,请👍三连支持&…...

汽车托运使用的场景
在托运车辆时,要仔细的检查车辆的性能,比如电瓶电量是否充足,发动机的性能是否良好,轮胎是否是正常的气压,冬季时需使用防冻液,车内禁止放易燃易爆物品。 托运时还需选择一家好的托运公司,首先要…...

机器学习 - 加油站数据分析
一、实验数据 数据集:“加油站数据.xls” 数据集介绍:该表记录了用户在11月和12月一天24小时内的加油信息,包括:持卡人标识(cardholder)、卡号(cardno)、加油站网点号(n…...
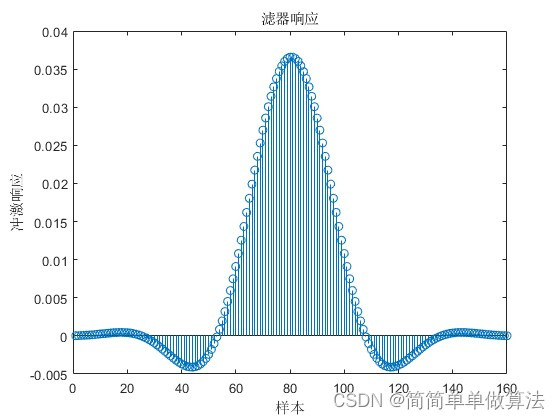
基于CMFB余弦调制滤波器组的频谱响应matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1、CMFB余弦调制滤波器组原理 4.2、CMFB调制过程 4.3、CMFB特点 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 ......................…...

helm一键部署grafana
一键部署命令 helm repo add prometheus-community https://prometheus-community.github.io/helm-charts helm repo update helm install prometheus prometheus-community/kube-prometheus-stack暴露服务 kubectl port-forward --address 0.0.0.0 deployment/prometheus-gr…...

pytorch复现_NMS
NMS(非极大值抑制)阈值是用于控制在一组重叠的边界框中保留哪些边界框的参数。当检测或识别算法生成多个边界框可能涵盖相同物体时,NMS用于筛选出最相关的边界框,通常是根据它们的置信度分数。 具体来说,NMS的工作原理…...
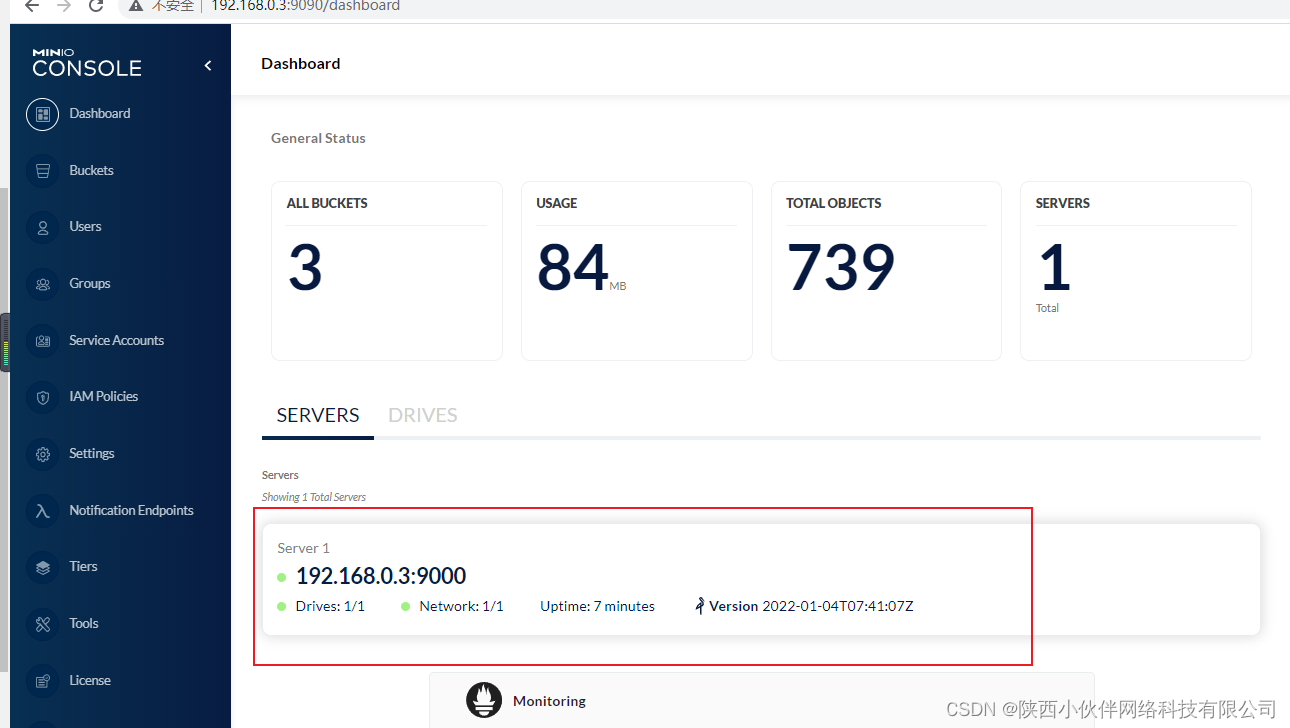
备份doris数据到minio
1、MINIO 设置 创建服务账户,记住ACCESS_KEY和SECRET_KEY 创建Buckets doris 设置region 在首页查看服务ip和端口号 2、创建S3备份库 因为minio是兼容S3协议的,所以可以通过s3协议链接minio。 CREATE REPOSITORY minio WITH S3 ON LOCATION "s3://…...

Linux中正则表达式等
grep命令:主要作用就是过滤查找文本内容 常用的选项有: -m 数字:匹配几次之后停止,按行匹配,不是按字符个数,例如 -v:取反 例如: -n:显示匹配的行号 例如: -c:仅显示匹配的行数,不显示匹配内…...

记一次并发问题 Synchronized 失效
记一次并发问题 Synchronized 失效 场景:为避免信息提交重复,给事务方法增加了synchronized修饰符,实际场景中仍然无法完全避免重复,原因是因为在第一个线程执行完synchronized代码段后,此时spring还未完成事务提交&a…...
手机平板摄像头如何给电脑用来开视频会议
环境: Iriun Webcam EV虚拟摄像头 钉钉会议 问题描述: 手机平板摄像头如何给电脑用来开视频会议 解决方案: 1.下载软件 手机端和电脑端都下载这个软件,连接同一局域网打开软件连接好 另外一款软件Iriun 也是一样操作 2.打…...
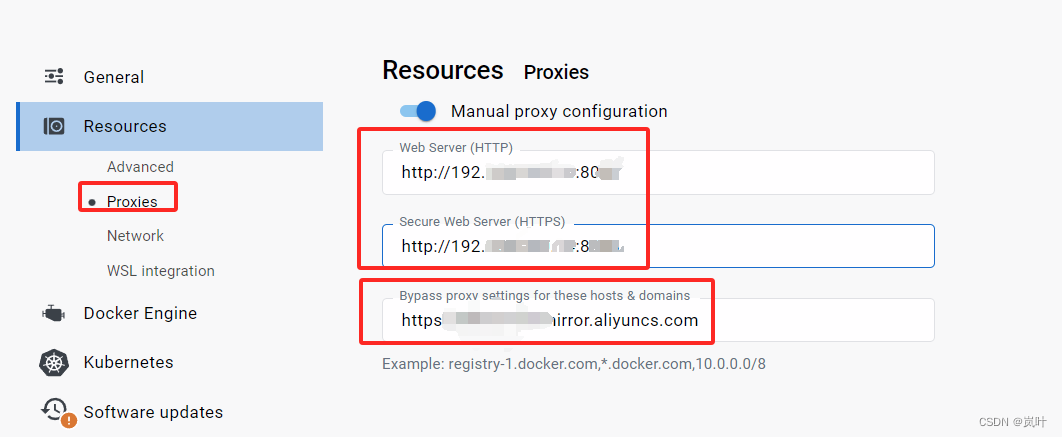
windows docker desktop 更换镜像 加速
最近 docker hub 访问不了; 经过研究 可以通过添加 代理镜像网址 添加代理服务器的方式 实现完美访问 1添加镜像网站 修改成国内镜像地址就能享受到飞一般的速度,但有一个问题,部分站点镜像不全或者镜像比较老,建议使用多个镜像站。 https…...

linux下多机器ssh免密码登录配置
20,21,22,23等4台机器配置ssh免密登陆 确认sshd配置 查看/etc/ssh/sshd_config文件,确认如下配置没有被注释掉: AuthorizedKeysFile .ssh/authorized_keys每一台机器修改hosts配置主机名(可选) 执行ssh命令,如…...
【IDEA使用maven package时,出现依赖不存在以及无法从仓库获取本地依赖的问题】
Install Parent project C:\Users\lxh\.jdks\corretto-1.8.0_362\bin\java.exe -Dmaven.multiModuleProjectDirectoryD:\学习\projectFile\study\study_example_service "-Dmaven.homeD:\Program Files\JetBrains\IntelliJ IDEA2021\plugins\maven\lib\maven3" "…...

Flink 统计接入的数据量-滚动窗口和状态的使用
1、概述 在生产场景值,经常需要和上游、下游对数,离线场景可以直接 group by 再 count ,但是实时场景中,如果使用 kafka 作为中间件,中间经过几个 job 的过滤转化后,再对照像 Doris 或 Clickhouse 中最终层…...
)
SpringBoot快速整合canal1.1.5(TCP模式)
SpringBoot快速整合canal1.1.5(TCP模式) 安装并配置MySQL主从⭐ 1:Docker安装MySQL8.0.28 docker pull mysql:8.0.282:创建目录: mkdir -p /usr/local/mysql8/data mkdir -p /usr/local/mysql8/log mkdir -p /usr/…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
