思维训练3
题目描述1
Problem - A - Codeforces

题目分析
样例1解释:
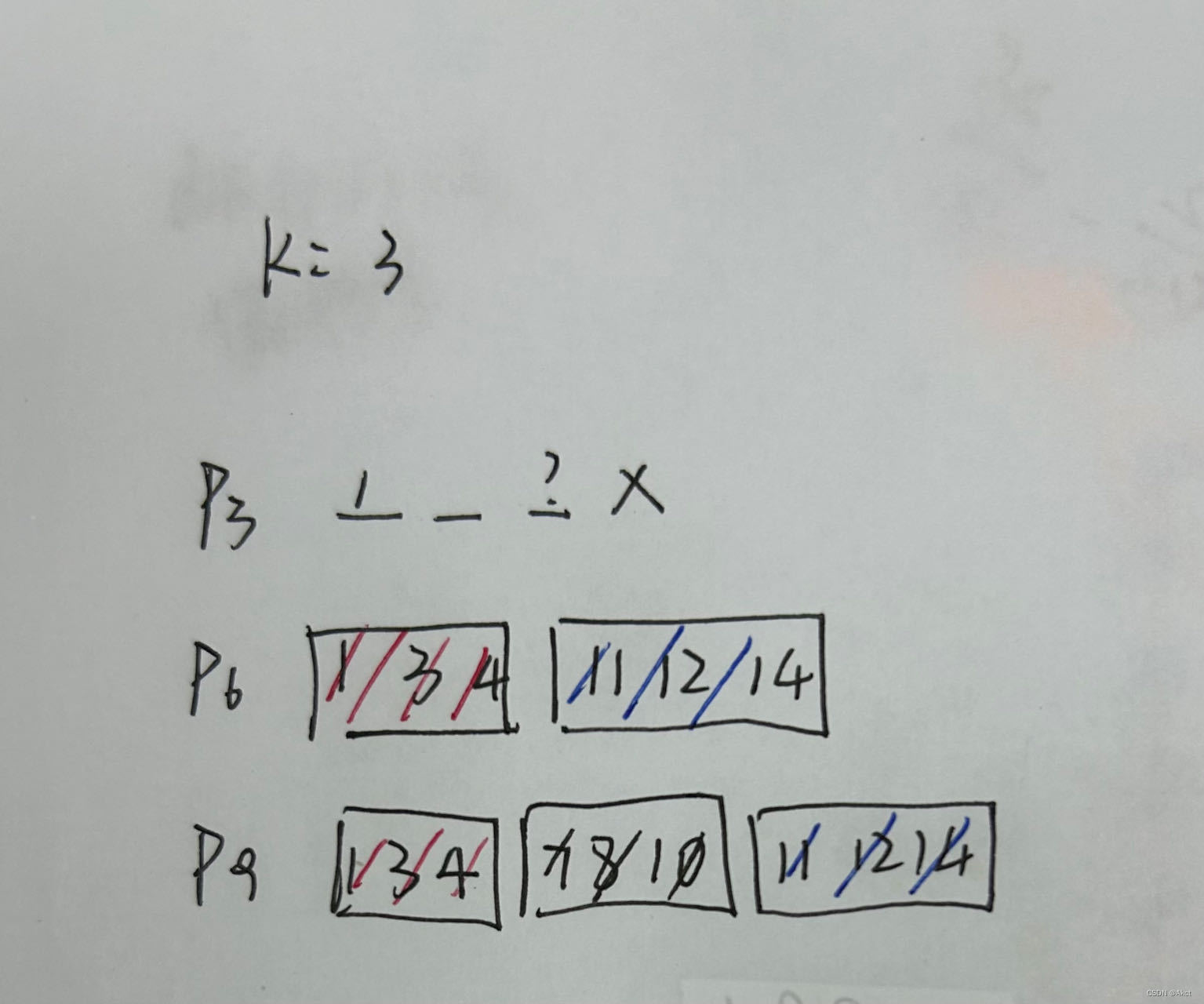
对于此题,我们采用贪心的想法,从1到n块数越少越好,故刚好符合最少的块数即可,由于第1块与第n块是我们必须要走的路,所以我们可以根据这两块砖的颜色进行分类判断。
如果这两块砖是一样的颜色,我们只需要判断这两块砖算上中间的颜色的总块数是否>=k即可。
如果这两块砖是不一样的颜色,我们需要分别从两端观察前面这部分的砖和后面这部分砖可以走的相同的颜色是否>=k即可
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
void solve()
{int n, k, c[N];cin >> n >> k;for(int i = 1; i <= n; i ++)cin >> c[i];if(c[1] == c[n]){int cnt = 0;for(int i = 2; i <= n - 1; i ++){if(c[i] == c[1])cnt ++; }if(cnt >= k - 2)cout << "YES" << '\n';else cout << "NO" << '\n';}else {int l = n, r = 1,kl = 0, kr = 0;for(int i = 1; i <= n && kl < k; i ++){if(c[i] == c[1]){kl ++;l = i;}}for(int i = n; i >= 1 && kr < k; i --){if(c[i] == c[n]){kr ++;r = i;}}if(kl == k && kr == k && l < r)cout << "YES" << '\n';else cout << "NO" << '\n'; }
}
int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int t;cin >> t;while(t --){solve();}return 0;
}题目描述2
Problem - B - Codeforces

题目样例示意:
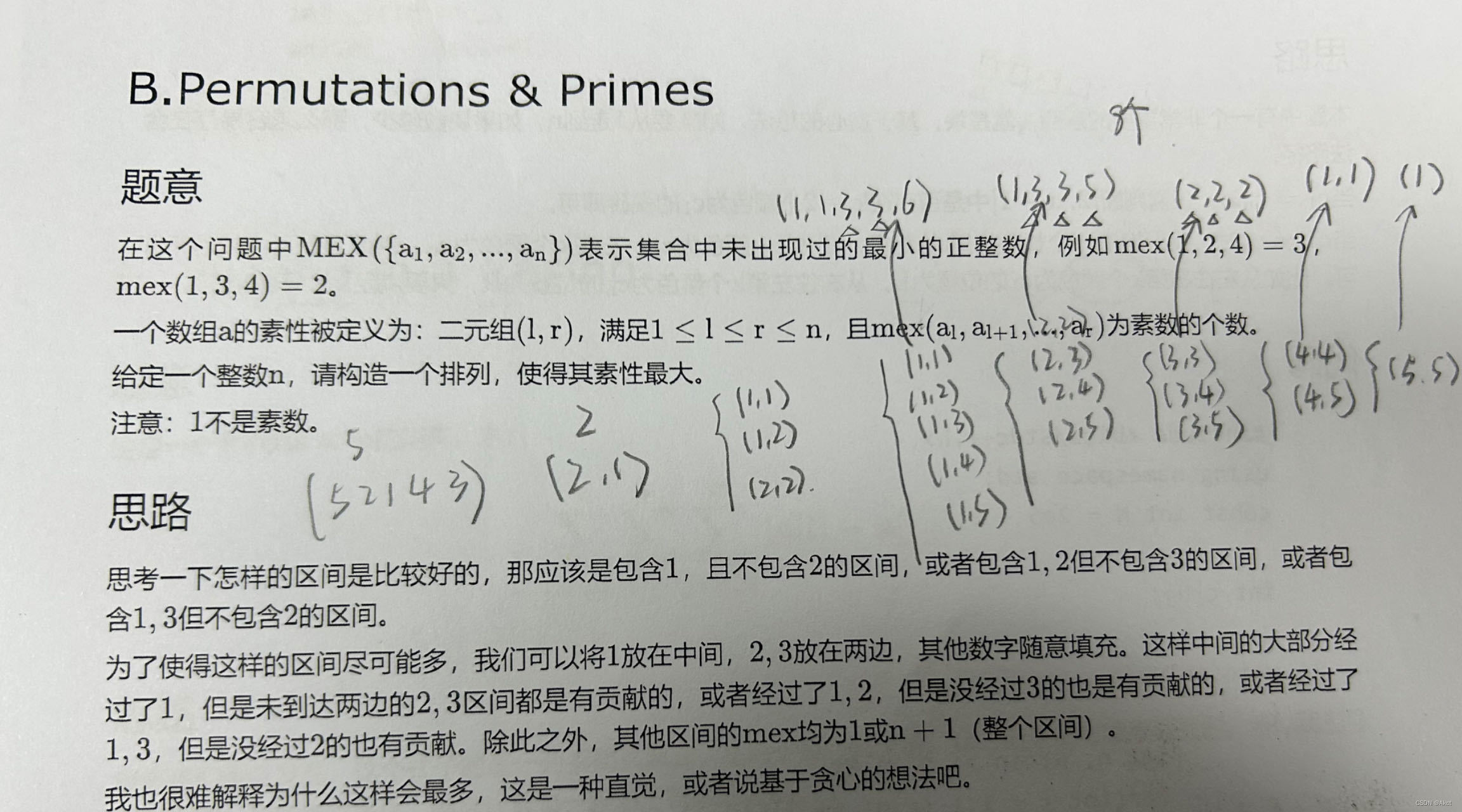
注意:找出的是排列也就是说数字不能重复,而且所有的数从小到大排序之后一定为连续的。
思考:什么是好区间?
包含1但是不包含2的区间(2)
包含1,2但是不包含3的区间(3)
包含1,3但是不包含2的区间(2)
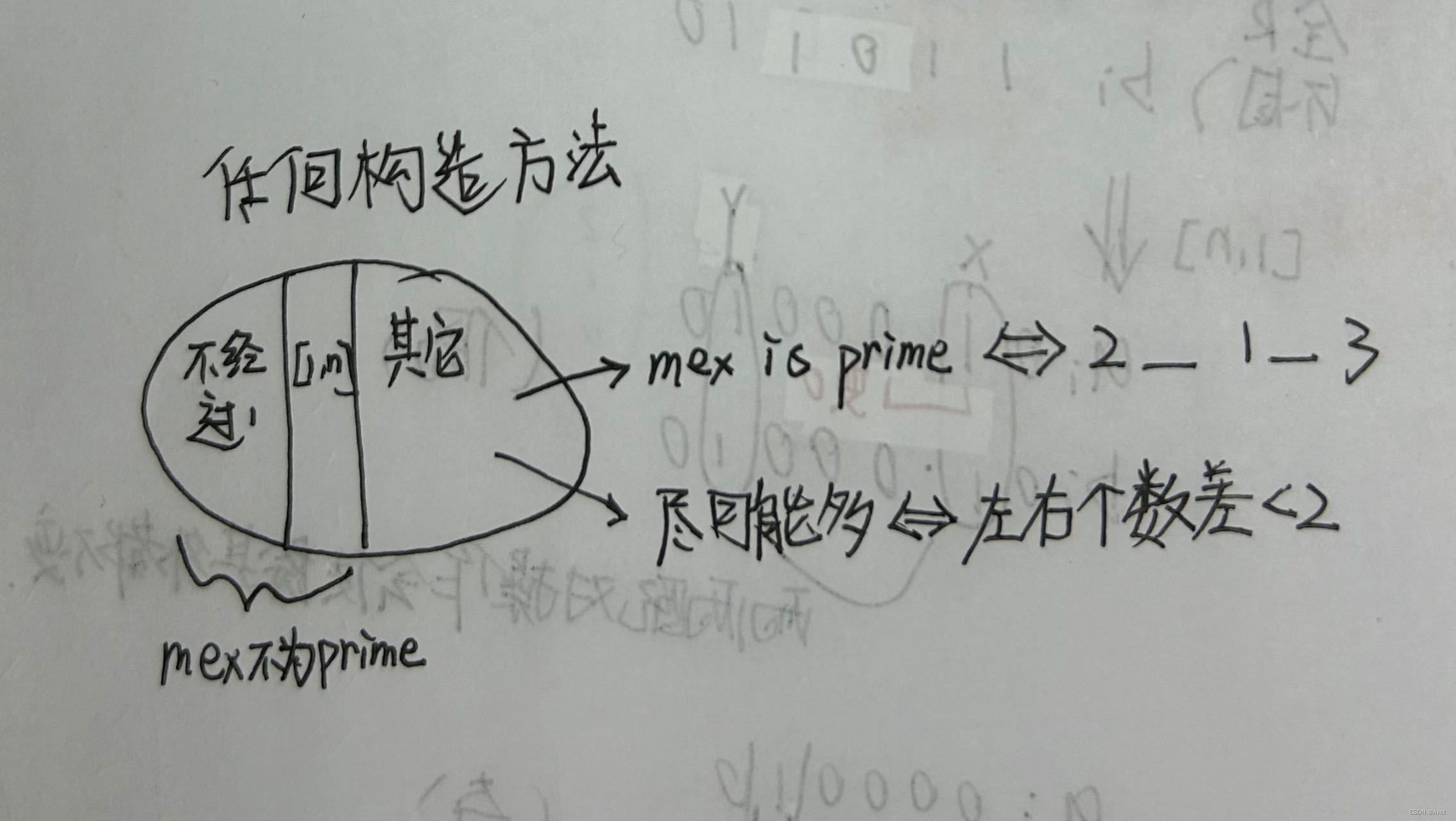
为了使这样的区间尽可能多
我们可以进行一个构造,题目要求在所有的区间中尽量使所有的素数结果最多我们可以将2和3放在两边,将1放在中间,这样中间的大部分经过了1,但是未到达两边的2,3区间都是有贡献的,或者经过了1,2,但是没经过3的也是有贡献的,或者经过了1,3但是没经过2的也有贡献。
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int a[N], n;
void solve()
{cin >> n;a[1] = 3, a[n] = 2;int x = (n + 1) / 2;a[x] = 1;int k = 3;for(int i = 2; i < x; i ++){k ++;a[i] = k; } for(int i = x + 1; i < n; i ++){k ++;a[i] = k;}for(int i = 1; i <= n; i ++)cout << a[i] << ' ';cout << '\n';
}
int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int t;cin >> t;while(t --){solve();}return 0;
}题目描述3
Problem - C - Codeforces
题目分析


此题我们需要掌握缩点的思想。
缩点:连续相同的字符变成一个字符即可
eg.00011110001011缩点成010101
需要不降序排列故左边0多好,"?"挨着哪个数就缩成哪个数,如果左右两边的数不一样就统一先按左边来缩数
#include<bits/stdc++.h>
using namespace std;
void solve()
{string s ;cin >> s;int n = s.size() ;for(int i = 0; i < n; i ++){if(i != 0 && s[i] == '?'){s[i] = s[i - 1]; } else if(i == 0 && s[i] == '?')s[i] = '0';} cout << s << '\n';
}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int t;cin >> t;while(t --){solve();}return 0;
}题目描述4
Problem - D - Codeforces

题目分析

由上图可知变化一次必然会进行一次颜色的翻转
R表示数字不同的一列,B表示数字相同的一列
故要么是全R要么是全B才能到达一个全B的终点
一次操作到全R两次操作就会回到全B,故我们需要进行操作绑定
两两配对操作会使得除了这两个数之外的所有数都不发生变化(操作绑定)
但是如果剩下一个数没有配对时,可以进行如图右下角的方法计算
将需要改变的1存入vector中,并将其中的不能配对的奇数的1单独取出计算,剩下的进行配对即可
注:若取出的数的位置不在1时就可以改变(1, x - 1),(1, x)
若取出的数的位置在1时就可以改变(x, n)(x + 1, n)
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5 + 10;
typedef pair<int, int> PII;
void solve()
{char a[N], b[N];int n;vector<PII> ans;vector<int> pos;cin >> n;cin >> a + 1 >> b + 1;bool flag1 = 0, flag2 = 0;for(int i = 1; i <= n; i ++){if(a[i] == b[i])flag1 = 1;else flag2 = 1;}if(flag1 && flag2){cout << "NO" << '\n';return;}if(flag2)//如果全是不相同的字符{ans.push_back({1, n});for(int i = 1; i <= n; i ++){if(a[i] == '0')a[i] = '1';else a[i] = '0';}}for(int i = 1; i <= n; i ++){if(a[i] == '1')pos.push_back(i);}if(pos.size() & 1){int x = pos.back();if(x == 1){ans.push_back({x, n});ans.push_back({x + 1, n});}else{ans.push_back({1, x - 1});ans.push_back({1, x});}pos.pop_back();}for(auto i : pos)ans.push_back({i, i});cout << "YES" << '\n' << ans.size() << '\n';for(auto i : ans){cout << i.first << ' ' << i.second << '\n'; }
}
int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int t;cin >> t;while(t --){solve();}return 0;
}题目描述5
Problem - E - Codeforces

题目分析

此题相当于找规律,从最大的数开始看起,第一个大于等于(n - 1)的平方数就是此处可以组成的平方数,发现会有连续的一段的平方数一样,判断限制条件,如果条件不满足就循环改数使其满足条件。
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int a[N];
void solve()
{bitset<N> vis;int n;cin >> n;int y = 0;while(y * y < n - 1)y ++;for(int i = n - 1; i >= 0; i --){while(y * y - i >= n || vis[y * y - i])y --;a[i] = y * y - i;vis[a[i]] = true;}for(int i = 0; i < n; i ++){cout << a[i] << ' ';}cout << '\n';
}
int main()
{int t;cin >> t;while(t --){solve();}return 0;
}相关文章:

思维训练3
题目描述1 Problem - A - Codeforces 题目分析 样例1解释: 对于此题,我们采用贪心的想法,从1到n块数越少越好,故刚好符合最少的块数即可,由于第1块与第n块是我们必须要走的路,所以我们可以根据这两块砖的…...

初识FFmpeg
前言 无意间见到群里的小伙伴展示视频工具。功能比较多,包括视频编码修改,画质处理,比例处理、名称提取,剪辑、标题拆解。因此开始了FFmpeg学习。以下摘自百度百科的解释。 FFmpeg是一套可以用来记录、转换数字音频、视频…...

分布式多主关系数据库的底线业务优势
当今的应用程序(包括企业应用程序)需要始终开启且始终可用,并且通常必须为全球用户提供服务,这些用户无论身在何处都希望获得几乎即时的响应时间。 应对这些挑战不仅仅意味着让用户更满意:每个能够解决低延迟和超高可…...
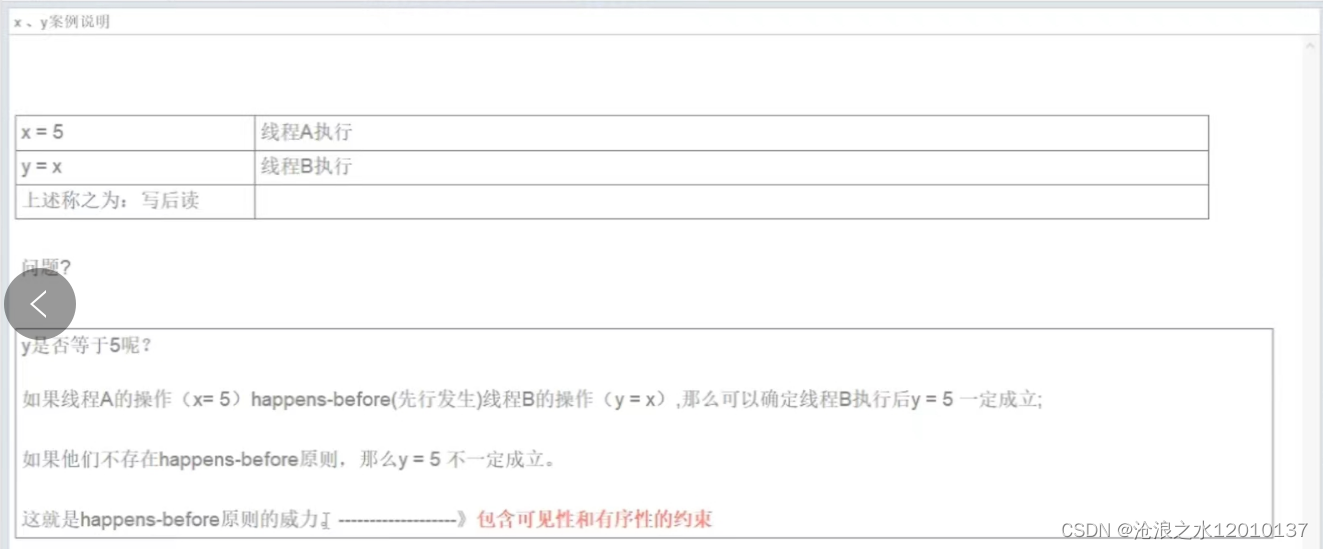
JMM讲解
一:为什么要有JMM,它为什么出现? CPU的运行并不是直接操作内存而是先把内存里面的数据读到缓存,而内存的读和写操作的时候会造成不一致的问题。JVM规范中试图定义一种Java内存模型来屏蔽掉各种硬件和操作系统的内存访问差异&…...
小程序获取头像和昵称的思路
小程序获取头像和昵称的基本方法是调用小程序自带的API wx.getUserProfile(),这也是小程序官方目前最推荐的做法。成功获取用户名头像之后,小程序允许保存调用的结果,以便下一次打开页面的时候自动显示头像和名字。保存用户名和头像并不是保存…...
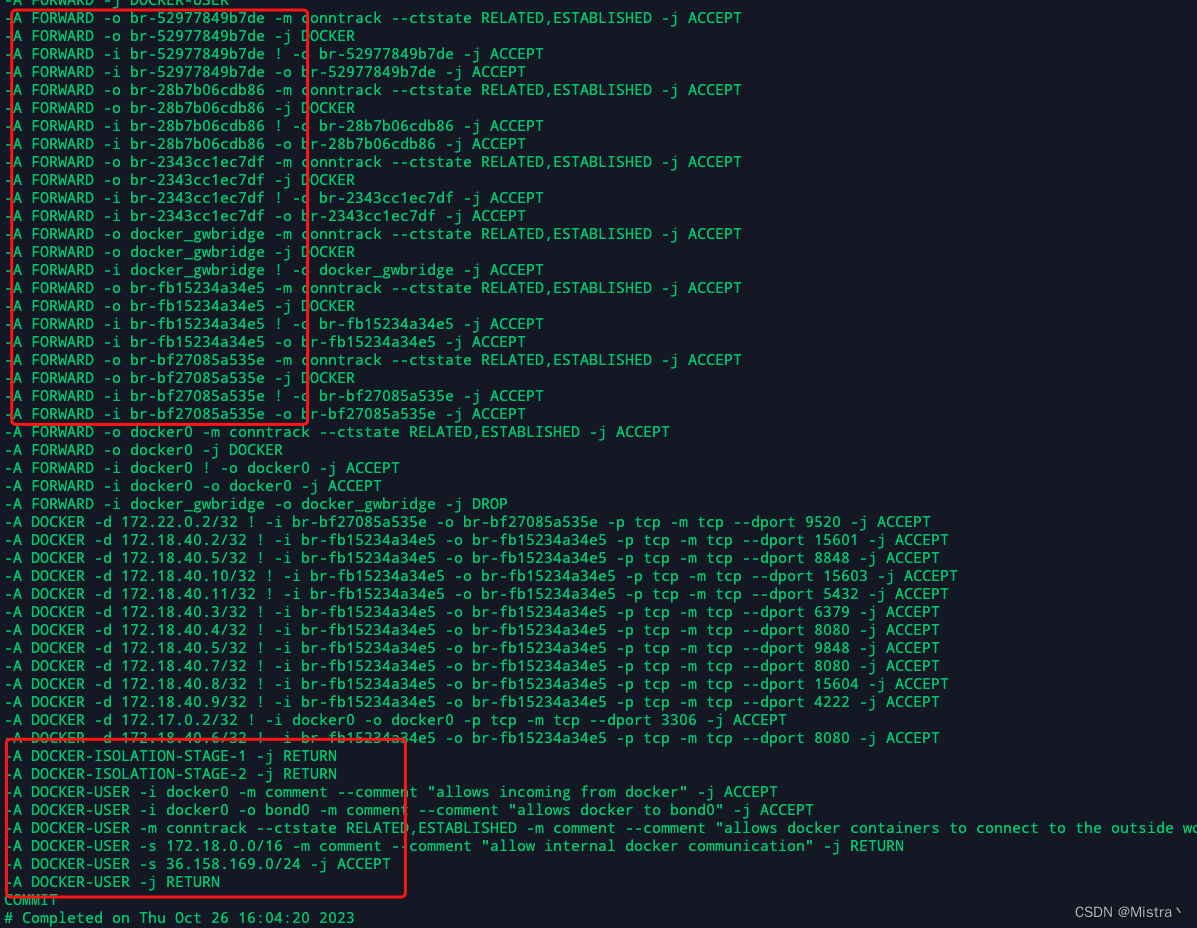
关于docker网络实践中遇到的问题
1.禁用docker自动修改iptables规则 查看docker.service文件/usr/lib/systemd/system/docker.service 默认在宿主机部署容器,映射了端口的话,docker能自己修改iptables规则,把这些端口暴露到公网。 如果要求这些端口不能暴露到公网…...
C#完成XML文档节点的自动计算功能
一个项目涉及XML文档中节点的自动计算,就是XML文档的每个节点都参与运算,要求: ⑴如果节点有计算公式则按照计算公式进行; ⑵如果节点没有计算公式则该节点的值就是所有子节点的值之和; ⑶节点有4种类型,计…...
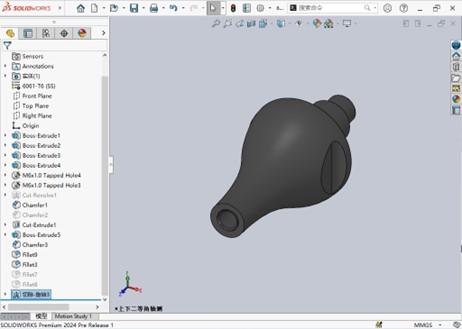
体验SOLIDWORKS旋转反侧切除增强 硕迪科技
大家在设计中经常使用的旋转切除命令在solidworks2024版本中迎来了新的增强,添加了旋转反侧切除选项。在设计过程中不必修改复杂的草图即可切除掉我们不需要的部分。使设计工作更加方便快捷。 打开零部件后,点击键盘上的S键并输入旋转切除以搜索该命令&a…...
)
分布式ID系统设计(3)
分布式ID系统设计第三集 id-service-SnowFlake方案 第二集说了id-service-Segment-DB可以生成趋势递增的ID,但是ID号是可以计算的。不太适用于一些订单ID生成的场景。因为存在数据暴露的风险 比如我可以对比两天的订单ID号来大致计算出公司一天的订单量。这个有点危险。 所以…...

工作备忘录【微信】
这工作备忘录【微信】里写自定义目录标题 unionid获取用户基本信息无 unionid EasyWeChat"overtrue/wechat": "^4.6" 与 "overtrue/wechat": "~3.1" 使用方式有异 unionid 微信 unionid 有关备忘录 获取用户基本信息无 unionid htt…...

Window下SRS服务器的搭建
---2023.7.23 准备材料 srs下载:GitHub - ossrs/srs at 3.0release 目前srs release到5.0版本。 srs官方文档:Introduction | SRS (ossrs.net) Docker下载:Download Docker Desktop | Docker 进入docker官网选择window版本直接下载。由…...

Canvas绘制简易雨滴碰撞效果
实现会动的图形,向下播放多张静态的图片。一秒内要大于屏幕刷新的帧数(60) 也就是每隔1/60s执行一次函数在每次绘制的正方形上添加一个背景色为白色蒙板。 效果图 源代码 <!DOCTYPE html> <html lang"en"><head><meta charset"…...

【五、http】go的http的信息提交
一、post提交的几种 form表单json文件 1、提交表单 //http的postfunc requstPost(){params : make(url.Values)params.Set("name", "kaiyue")params.Set("age", "18")formDataStr : []byte(params.Encode())formDataByte : bytes.N…...

第六讲:VBA与ACCESS的ADO连接中,所涉及的对象
《VBA数据库解决方案》教程(10090845)是我推出的第二套教程,目前已经是第二版修订了。这套教程定位于中级,是学完字典后的另一个专题讲解。数据库是数据处理的利器,教程中详细介绍了利用ADO连接ACCDB和EXCEL的方法和实…...
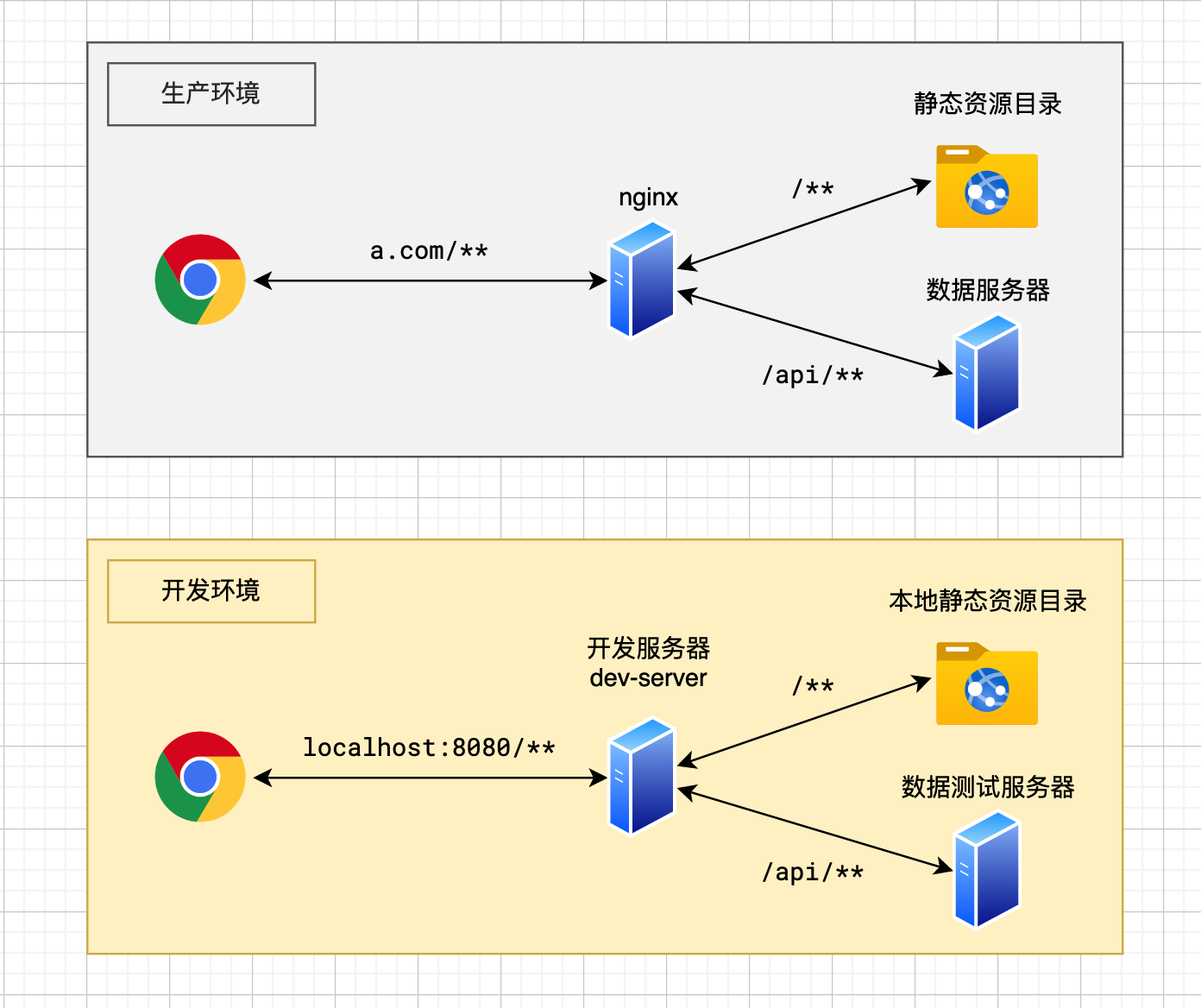
【计算机网络】同源策略及跨域问题
1. 同源策略 同源策略是一套浏览器安全机制,当一个源的文档和脚本,与另一个源的资源进行通信时,同源策略就会对这个通信做出不同程度的限制。 同源策略对 同源资源 放行,对 异源资源 限制。因此限制造成的开发问题,称…...

uniapp在APP端使用swiper进行页面不卡顿滑动
uniapp在APP端使用swiper进行页面会卡顿,主要是渲染的数据有点多,这里只渲染三个数据就不好那么卡顿了,每次滑动后更新数据 <view><swiper change"changePoint" circular :disable-touch"disableTouch"><…...

遗憾
《遗憾》 文/罗光记 岁月匆匆如梦过, 回首往事泪沾裳。 遗憾犹存心深处, 青春岁月已成伤。...

hustoj 平台
1.大部分功能和选项的开关和参数调整都在配置文件中,安装后几个重要配置文件的位置如下: /home/judge/etc/judge.conf #判题judged/judge_client /home/judge/src/web/include/db_info.inc.php #Web debian-sys-maint gdfNPYOdITxtDEK1 修改MySQl管…...

如何使用Scrapy提取和处理数据
目录 一、安装和设置Scrapy 二、创建爬虫 三、提取数据 四、处理数据 五、存储数据 六、进阶操作 七、注意事项 总结 Scrapy是一个强大且灵活的Python库,用于创建网页爬虫,提取和处理数据。本文将为您深入讲解如何使用Scrapy进行数据处理&#x…...

拟合与过拟合
拟合跟过拟合 过拟合:将泛化误差分解为偏差跟方差 偏差:学习者不断学习相同错误事物的倾向 方差:学习随机信号而不考虑真实情况的趋势 过拟合:所建的机器学习模型或者深度学习模型在训练样本中表现得过于优越,导致测试数据集表现…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
