LeetCode算法题解| 669. 修剪二叉搜索树、108. 将有序数组转换为二叉搜索树、538. 把二叉搜索树转换为累加树
一、LeetCode 669. 修剪二叉搜索树
题目链接:669. 修剪二叉搜索树
题目描述:
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:

输入:root = [1,0,2], low = 1, high = 2 输出:[1,null,2]
示例 2:

输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3 输出:[3,2,null,1]
提示:
- 树中节点数在范围
[1, 104]内 0 <= Node.val <= 104- 树中每个节点的值都是 唯一 的
- 题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
算法分析:
利用递归和回溯思想。
写出两个方法分别找出当前树的最大直节点以及最小值节点。
public TreeNode Max(TreeNode root) {//找出二叉搜索树的最大值节点if(root == null) return root;else if(root.right != null) return Max(root.right);else return root;}public TreeNode Min(TreeNode root) {//找到二叉搜索树的最小值节点if(root == null) return root;else if(root.left != null) return Min(root.left);else return root;}在递归函数中,
如果当前节点为空,直接返回null。
如果当前节点的值大于目标区间的最大值high,说明当前节点以及右子树的所有节点值都不在区间范围内,剪去当前节点以及右子树。
如果当前节点的值小于目标区间的最小值low,说明当前节点以及左子树的所有节点值都不在目标区间范围内,减去当前节点以及左子树。
如果当前树的最大直小于目标区间最大值high,并且最小值大于目标区间最小值low,即当前树的所有节点值都在目标区间范围内,此时可以直接返回当前树的根节点。
以上四种情况排除之后,当前的情况是,根节点的值再目标区间范围内,但是最小值和最大值两个节点当中至少有一个不在目标区间范围内。
此时我们要分别向左右子树递归去修剪那些不合理的节点,然后再将当前的节点返回就可以啦!
代码如下:
class Solution {public TreeNode Max(TreeNode root) {//找出二叉搜索树的最大值节点if(root == null) return root;else if(root.right != null) return Max(root.right);else return root;}public TreeNode Min(TreeNode root) {//找到二叉搜索树的最小值节点if(root == null) return root;else if(root.left != null) return Min(root.left);else return root;}public TreeNode trimBST(TreeNode root, int low, int high) {if(root == null) return null;//如果当前节点为空,直接返nullelse if(root.val > high) return trimBST(root.left, low, high);//如果当前节点的值大于high,那么说明右子树的全部节点值都不在目标区间内,向左递归去寻找合理的节点else if(root.val < low) return trimBST(root.right, low, high);//反之如果当前节点的值小于low,说明当前节点及左子树全部节点的值都不在目标区间内,向右递归去寻找合理的节点else if(Max(root).val <= high && Min(root).val >= low) return root;//如果当前树的最大值小于等于high并且最小值大于等于low,即当前树在目标区间范围内,则可以直接返回当前树的根节点else {//到这儿的情况是,根节点的值在目标区间范围内,儿最大值和最小值至少有一个不在区间范围root.left = trimBST(root.left, low, high);//向左子树递归去修剪不合理的节点,再返回左子树的根节点root.right = trimBST(root.right, low, high);//向右递归去修剪右子树的不合理节点,在返回根节点return root;//此时左右子树都修剪完了,返回当前节点}}
}二、
LeetCode108. 将有序数组转换为二叉搜索树
题目链接:108. 将有序数组转换为二叉搜索树
题目描述:
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:

输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:

示例 2:

输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
算法分析
根据二叉搜索树的性质(每个节点的做左右子树高度差不超过一),题目给我们的是一个有序的数组。
那么我们每次只去要找道数组的中间元素作为树的根节点,然后将数组从中间分割成两个数组,左数组用来创建左子树,右数组用来创建右子树。
然后向左右数组依次递归下去,最后返回根节点即可。
代码如下:
class Solution {public TreeNode BuildTree(int[] nums, int left, int right) {//区间利用左闭右开原则if(left >= right) return null;//如果左区间大于等于有区间返回空节点if(right - left == 1) return new TreeNode(nums[left]);//如果区间内只有一个元素,将当前元素创建成节点后返回else {//区间内有多个元素时int mid = left + (right - left) / 2;//找到这段区间内的中间元素TreeNode node = new TreeNode(nums[mid]);//将中间元素创建成节点,以该节点为树的根节点node.left = BuildTree(nums, left, mid);//利用递归创建左子树node.right = BuildTree(nums, mid + 1, right);//利用递归创建右子树return node;//返回当前书的根节点}}public TreeNode sortedArrayToBST(int[] nums) {return BuildTree(nums, 0, nums.length);}
}三、538. 把二叉搜索树转换为累加树
题目链接:538. 把二叉搜索树转换为累加树
题目描述:
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意:本题和 1038: 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 相同
示例 1:
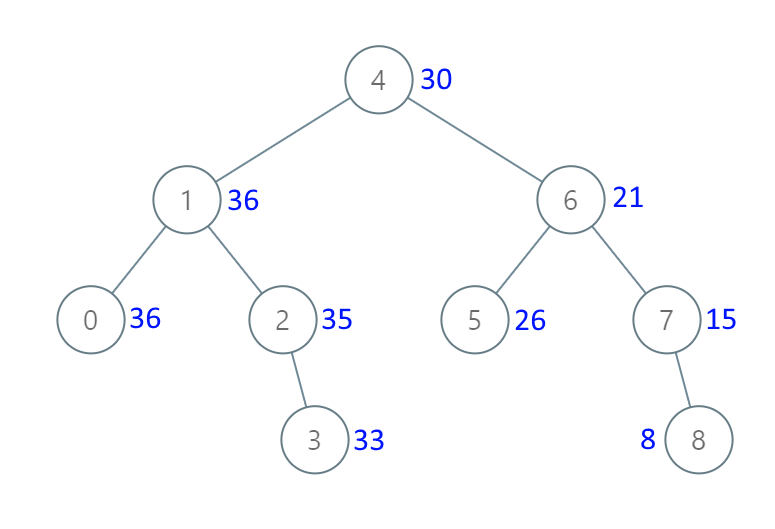
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1] 输出:[1,null,1]
示例 3:
输入:root = [1,0,2] 输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1] 输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
算法分析:
利用右中左序遍历,当前节点的是值加等于前一个节点的值。
代码如下:
class Solution {int pre = 0;//记录前一个节点的值public void midTravel(TreeNode cur) {//右中左序遍历if(cur == null) return;midTravel(cur.right);cur.val += pre;pre = cur.val;midTravel(cur.left);}public TreeNode convertBST(TreeNode root) {midTravel(root);return root;}
}总结
修剪二叉搜索树、构造二叉搜索树、累加树。
相关文章:

LeetCode算法题解| 669. 修剪二叉搜索树、108. 将有序数组转换为二叉搜索树、538. 把二叉搜索树转换为累加树
一、LeetCode 669. 修剪二叉搜索树 题目链接:669. 修剪二叉搜索树 题目描述: 给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变…...

直播界很火的无线领夹麦克风快充方案 Type-C接口 PD快充+无线麦克风可同时进行
当前市场上流行一款很火的直播神器,无线领夹麦克风(MIC),应用于网红直播,网课教学,采访录音,视频录制,视频会议等等场景。 麦克风对我们来说并不陌生,而且品类有很多。随…...
Jmeter 汉化中文语言
找到 bin -> jmeter.propertise 修改参数:languageen --> languagazh_CN OK!...
centos9 stream 下 rabbitmq高可用集群搭建及使用
RabbitMQ是一种常用的消息队列系统,可以快速搭建一个高可用的集群环境,以提高系统的弹性和可靠性。下面是搭建RabbitMQ集群的步骤: 基于centos9 stream系统 1. 安装Erlang和RabbitMQ 首先需要在所有节点上安装Erlang和RabbitMQ。建议使用官…...

代码随想录算法训练营第10天|232. 用栈实现队列 225. 用队列实现栈
JAVA代码编写 232. 用栈实现队列 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除…...

线上Kafka集群如何调整消息存储时间
这里是weihubeats,觉得文章不错可以关注公众号小奏技术,文章首发。拒绝营销号,拒绝标题党 Kafka版本 kafka_2.13-3.5.0 背景 Kafka 默认消息存储时间为7天,实际线上的业务使用Kafka更多的是一些数据统计之类的业务,大多是朝生夕…...
[迁移学习]DA-DETR基于信息融合的自适应检测模型
原文标题为:DA-DETR: Domain Adaptive Detection Transformer with Information Fusion;发表于CVPR2023 一、概述 本文所描述的模型基于DETR,DETR网络是一种基于Transformer的目标检测网络,详细原理可以参见往期文章:…...
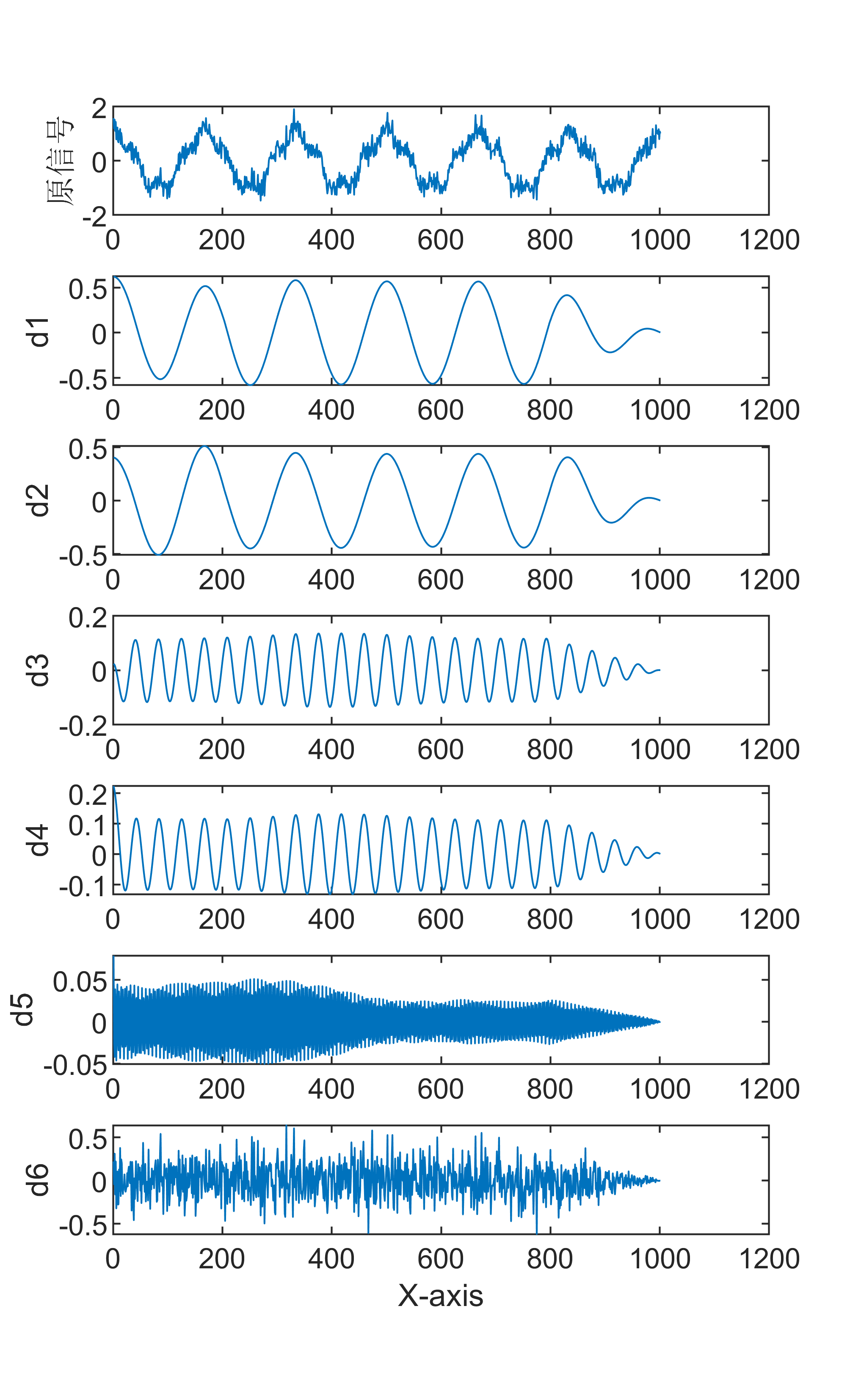
【MATLAB】全网唯一的13种信号分解+FFT傅里叶频谱变换联合算法全家桶
有意向获取代码,请转文末观看代码获取方式~ 大家吃一顿火锅的价格便可以拥有13种信号分解FFT傅里叶频谱变换联合算法,绝对不亏,知识付费是现今时代的趋势,而且都是我精心制作的教程,有问题可随时反馈~也可单独获取某一…...
Nginx安装与配置
1.下载安装包 官网下载地址:nginx: download 可以先将安装包下载到本地再传到服务器,或者直接用wget命令将安装包下载到服务器,这里我们直接将安装包下载到服务器上。未安装wget命令的需要先安装wget,yum install -y wget [root…...

linux笔记总结-基本命令
参考: 1.Linux 和Windows比 比较 (了解) 1. 记住一句经典的话:在 Linux 世界里,一切皆文件 2. Linux目录结构 /lib • 系统开机所需要最基本的动态连接共享库,其作用类似于Windows里的DLL文件。几 乎所有…...
[PHP]禅道项目管理软件ZenTaoPMS源码包 v16.4
禅道项目管理软件ZenTaoPMS一键安装包是一款国产的开源项目管理软件。它集产品管理、项目管理、质量管理、文档管理、组织管理和事务管理于一体,是一款专业的研发项目管理软件,完整地覆盖了项目管理的核心流程。注重实效的管理思想,合理的软件…...

Required String parameter ‘name‘ is not present
[org.springframework.web.bind.MissingServletRequestParameterException: Required String parameter name is not present] 服务端有参数name,客户端没有传上来...
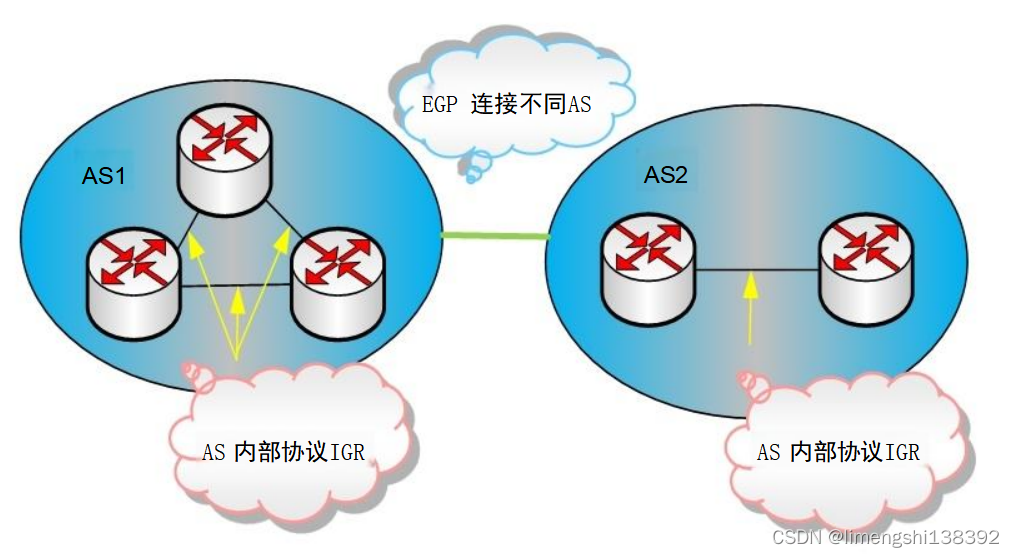
路由器基础(五): OSPF原理与配置
开放式最短路径优先 (Open Shortest Path First,OSPF) 是一个内部网关协议 (Interior Gateway Protocol,IGP),用于在单一自治系统(Autonomous System,AS) 内决策路由。OSPF 适合小型、中型、较大规模网络。OSPF 采用Dijkstra的最短路径优先算法 (Shortest Pat…...
Leetcode1128. 等价多米诺骨牌对的数量
Every day a Leetcode 题目来源:1128. 等价多米诺骨牌对的数量 解法1:暴力 代码: class Solution { public:int numEquivDominoPairs(vector<vector<int>> &dominoes){int n dominoes.size(), count 0;for (int i 0;…...
Dev-C调试的基本方法2-2
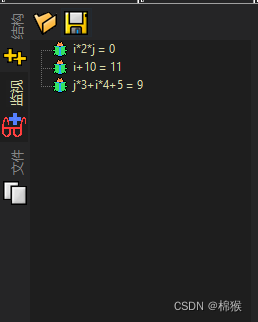
3.3 跳出函数 在图6所示的状态下,点击单步调试(F7)会继续调试下一行,而如果想结束在函数中的调试,则点击图4③所示的跳出函数,或CtrlF8按键跳出f()函数,程序将会停在图5所示的第11行处。 3.4 …...

企业之间的竞争,ISO三体系认证至关重要!
ISO三体系认证是指ISO 9001质量管理体系认证、ISO 14001环境管理体系认证、ISO 45001(OHSAS18001)职业健康安全管理体系认证。企业(组织)自愿申请、通过ISO三体系认证,并贯彻落实,确实能获益多多。 ISO 9001质量管理体系 我们经…...
node教程(四)Mongodb+mongoose
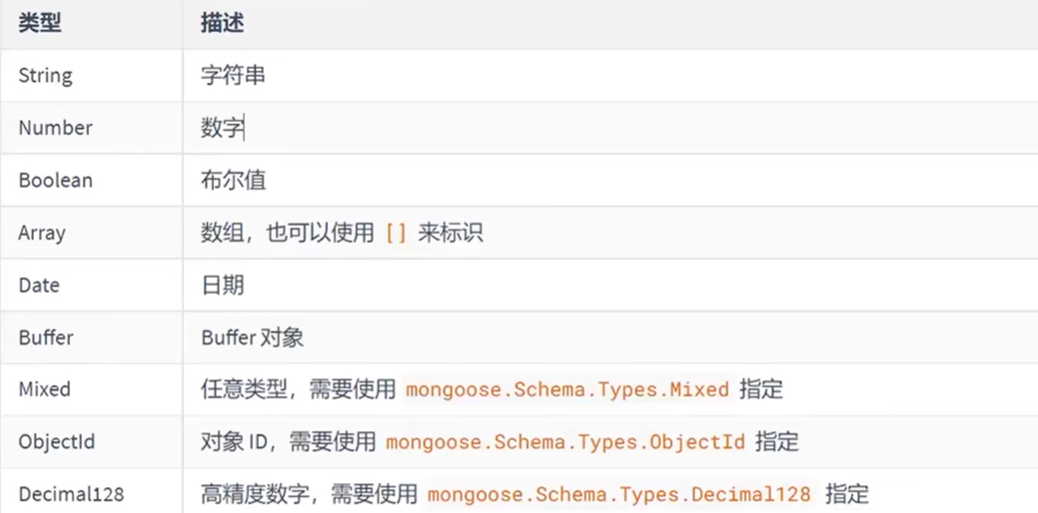
文章目录 一、mongodb1.简介1.1Mongodb是什么?1.2数据库是什么?1.3数据库的作用1.4数据库管理数据的特点 2.核心概念3.下载安装与启动4.命令行交互4.1数据库命令4.3文档命令 二、Mongoose1.介绍2.作用3.使用流程4.插入文档5.mongoose字段类型 一、mongod…...

作为一个初学者,该如何入门大模型?
在生成式 AI 盛行的当下,你是否被这种技术所折服,例如输入一段简简单单的文字,转眼之间,一幅精美的图片,又或者是文笔流畅的文字就展现在你的面前。 相信很多人有这种想法,认为生成式 AI 深不可测…...

编译支持GPU的opencv,并供python的import cv2调用
下载opencv和opencv_contrib,cmake过程中要下载的一些包可以手动下载配置,如果网络较好,也可以等待自动下载。主要记录的是cmake命令: cmake -D CMAKE_BUILD_TYPERELEASE \-D BUILD_opencv_python3YES \-D CMAKE_INSTALL_PREFIX/…...

Bug记录
那些年写过的很小的bug: Bug1: if args.model IRNN or irnn:# some code这实际上不会按你期望的方式工作。原因在于 ‘irnn’ 是一个非空的字符串,因此它在布尔上下文中被视为 True。所以条件总是为真,而不会考虑 args.model 的…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
