数模国赛——多波束测线问题模型建立研究分析
第一次参加数模国赛,太菜了~~~~意难平
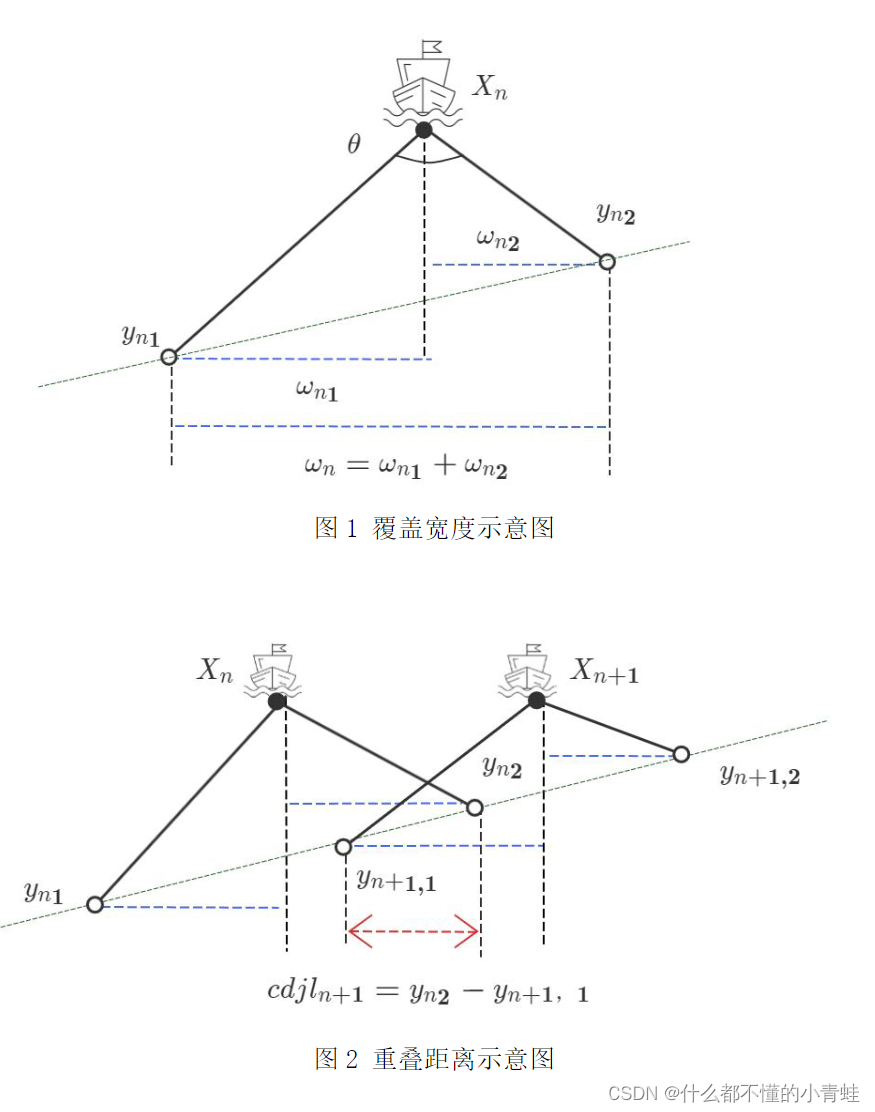
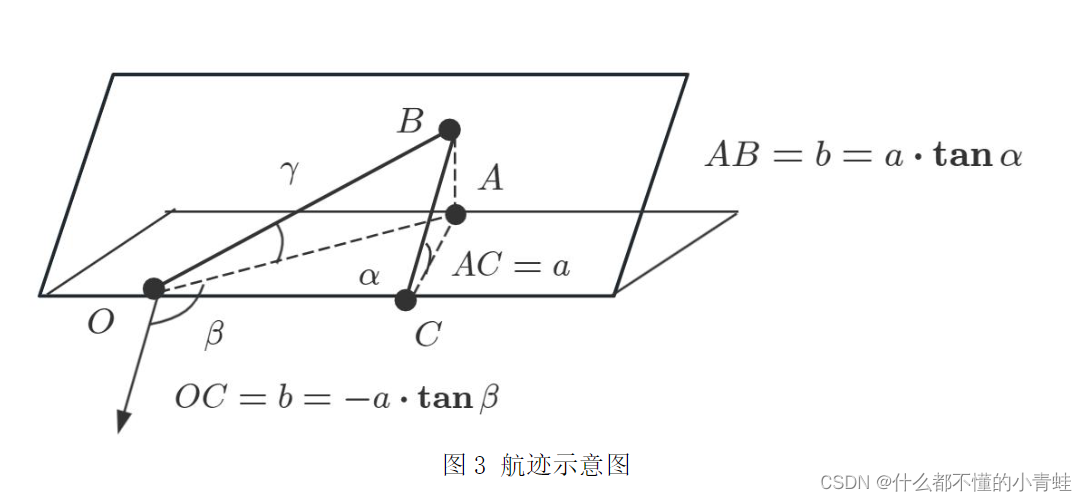
问题一
画出与测线方向垂直的平面和海底坡面的交线构成一条与水平面夹角为𝐀的斜线的情况下的示意图进行分析,将覆盖宽度分为左覆盖宽度和右覆盖宽度,求出它们与海水深度和𝐀、𝐀(复制的原因,没复制对,懒得改了)的关系。根据所列关系式,我们先计算出各个点位的海水深度,再求出覆盖宽度与重叠率,得出在 测线距中心点处的距离-600m 时的海水深度 为85.711553m,覆盖宽度为 297.3525571m,与前一条测线的重叠率为 33.639959%,具体计算结果如表 1 所示。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
pi = math.pi
tan1_point5=math.tan(1.5/180*pi)
angle_degrees = 1.5
angle_radians = math.radians(angle_degrees)
tan_value = math.tan(angle_radians)##事先算出 tan1.5 的值
print("tan(1.5 degrees) =", tan_value)
angle_degrees1 = 60
angle_radians1 = math.radians(angle_degrees1)
tan_value1 = math.tan(angle_radians1)##事先算出 tan60 的值
m=200*tan_value
##分别求出海水深度然后合并
value=70
2
ans1=[]
for i in range(1,5):
ans1.append(value-i*m)
ans1.reverse()
ans1.append(70)
ans2=[]
for i in range(1,5):
ans2.append(value+i*m)
D=ans1+ans2
D.reverse()
##计算覆盖宽度 W
w1=[]
w2=[]
W=[]
for i in range(len(D)):
x1=(D[i]*tan_value1)/(1-tan_value1*tan_value)
x2=(D[i]*tan_value1)/(1+tan_value1*tan_value)
w1.append(x1)
w2.append(x2)
W.append(x1+x2)
print(w1)
print(w2)
print(W)
##计算重叠率
x=[-800,-600,-400,-200,0,200,400,600,800]
y1=[]
y2=[]
for i in range(len(W)):
y1.append(x[i]-w1[i])
y2.append(x[i]+w2[i])
print(y1)
print(y2)
chongdie=[]
for i in range(1,len(W)):
chongdie.append((y2[i-1]-y1[i])/(y2[i-1]-y1[i-1]))
print(chongdie)
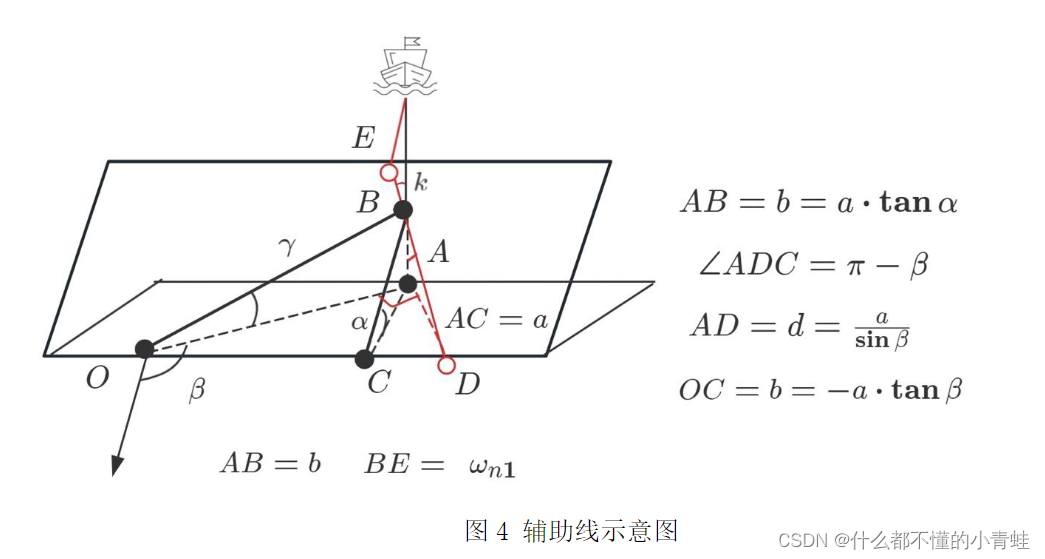
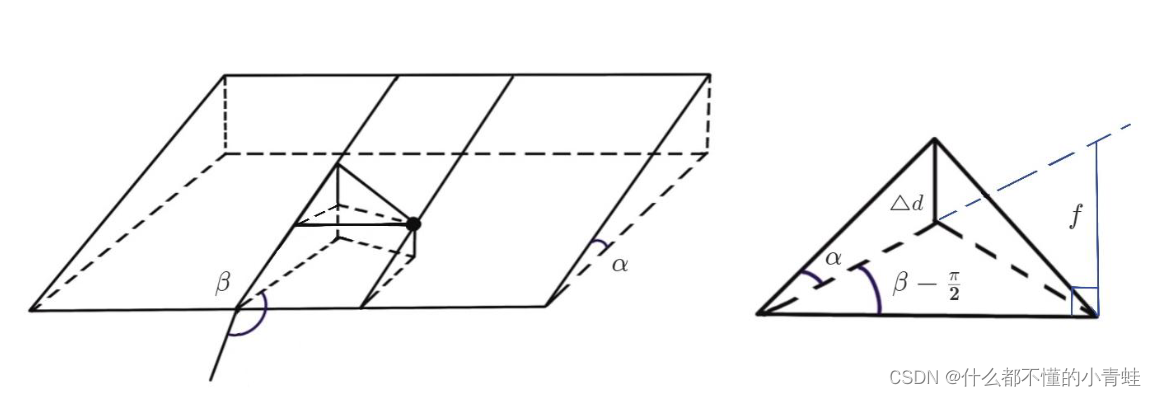
问题二
clc
clear
3
format long;%设置长小数格式
a=1.5/180*pi;
t=8;
D0=120;
theta=120/180*pi;
d=0.3*1852;%海里转化成米
for nbeta=1:1:t
beta=(nbeta-1)*pi*(360)/t*(t-1)/180/(t-1);
%检查 beta+pi/2 是否是 pi 的倍数
%如果 beta+pi/2 是 pi 的倍数,那么将 k1 设置为 0
%并将 k 设置为 a 的正切值的绝对值。
if mod(beta+pi/2,pi)==0;
k1=0;
k=abs(tan(a));
else
k=abs(tan(a)/sqrt(1+(tan(beta+pi/2))^2));
if 3*pi/2 > beta && pi/2 < beta;
k1=-tan(a)/sqrt(1+(tan(beta))^2);
else
k1=tan(a)/sqrt(1+(tan(beta))^2);
end
end
%深度计算
for n=1:1:t
x=(n-1)*d;
D(nbeta,n)=D0+x*k1;
end
%计算 w
for m=1:1:t
w1(nbeta,m)=D(nbeta,m)*sin(theta/2)/sin(pi/6-atan(k));
w2(nbeta,m)=D(nbeta,m)*sin(theta/2)/sin(pi/6+atan(k));
W(nbeta,m)=(w1(nbeta,m)+w2(nbeta,m))*cos(atan(k));
end
end
问题3
import numpy as np
import math
import geatpy as ea
class MyProblem(ea.Problem):
def __init__(self):
4
name = 'MyProblem'
M = 1
maxormins = [1]
-1:
Dim = 2 )
varTypes = [0] * Dim
lb = [math.pi/2, 0]
ub = [ math.pi, 2*1852]
lbin = [ 0, 0]
ubin = [ 0, 0]
# 调用父类构造方法完成实例化
ea.Problem.__init__(self,
name,
M,
maxormins,
Dim,
varTypes,
lb,
ub,
lbin,
ubin)
def evalVars(self, Vars): # 目标函数
beta= Vars[:, [0]]
f = Vars[:, [1]]
score = 4*1852*1852*2/(-np.cos(beta)*f)
#先把角度转化为弧度
angle_degrees_1 = 1.5
angle_radians_1 = math.radians(angle_degrees_1)
angle_degrees_60 = 60
angle_radians_60 = math.radians(angle_degrees_60)
k=np.arctan(1/(np.sin(beta)*np.tan(angle_radians_1)))
D=[]
for d in range(23,216):
D.append(abs(np.sin(k)*d*np.sin(angle_radians_60)/np.sin(k-angle_radians_60))+abs(np.sin(k)*(d+f*np.si
n(beta)*np.tan(angle_radians_1))*np.sin(angle_radians_60)/np.sin(k+angle_radians_60))
+f*np.cos(beta)-0.2*d*np.sin(angle_radians_60)*(abs(np.sin(k)/np.sin(k+angle_radians_60))+abs(np.sin(k
)/np.sin(k-angle_radians_60))))
D.append(0.1*d*np.sin(angle_radians_60)*(abs(np.sin(k)/np.sin(k+angle_radians_60))+abs(np.sin(k)/np.si
n(k-angle_radians_60))))
5
-abs(np.sin(k)*d*np.sin(angle_radians_60)/np.sin(k-angle_radians_60))+abs(np.sin(k)*(d+f*np.sin(beta)*n
p.tan(angle_radians_1))*np.sin(angle_radians_60)/np.sin(k+angle_radians_60))
+f*np.cos(beta)
CV=np.hstack(D)
return score, CV
if __name__ == '__main__':
# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.soea_DE_rand_1_bin_templet(
problem,
ea.Population(Encoding='RI', NIND=100),
MAXGEN=200,
logTras=1)
algorithm.mutOper.F = 0.5
algorithm.recOper.XOVR = 0.7
# 求解
res = ea.optimize(algorithm,
verbose=True,
drawing=1,
outputMsg=True,
drawLog=False,
saveFlag=True)
print(res)
问题4
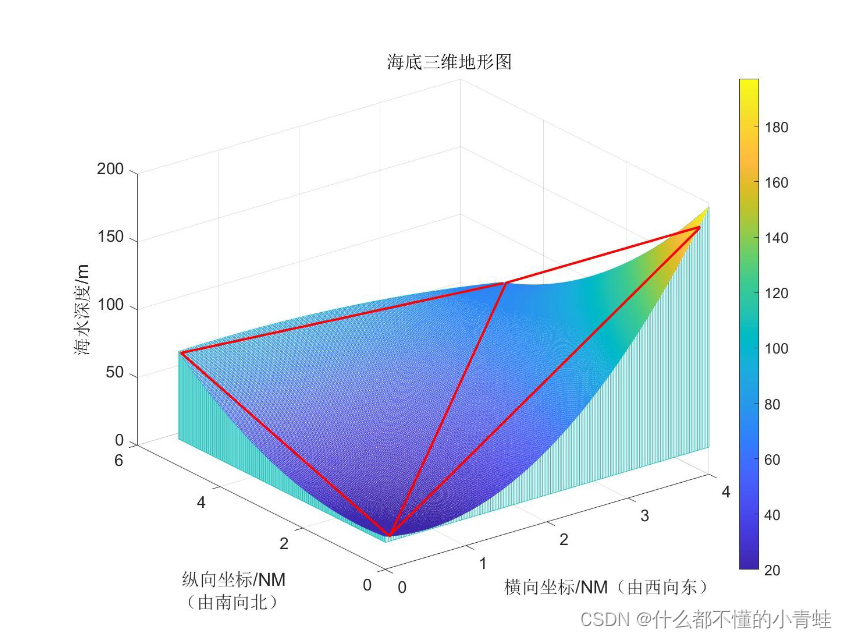
%读取数据
[X1,X2,X3]=xlsread("C:\Users\JJH\Desktop\CUMCM2023Problems\B 题\附件.xlsx");
x=X1(1,2:end);
y=X1(2:end,1);
z=X1(2:end,2:end);
cha=diff(z,1,2);
he=sum(cha(1,1:end));
average=he/250
[X Y]=meshgrid(x,y);
subplot(3,2,[1 2]);
meshz(X,Y,z);
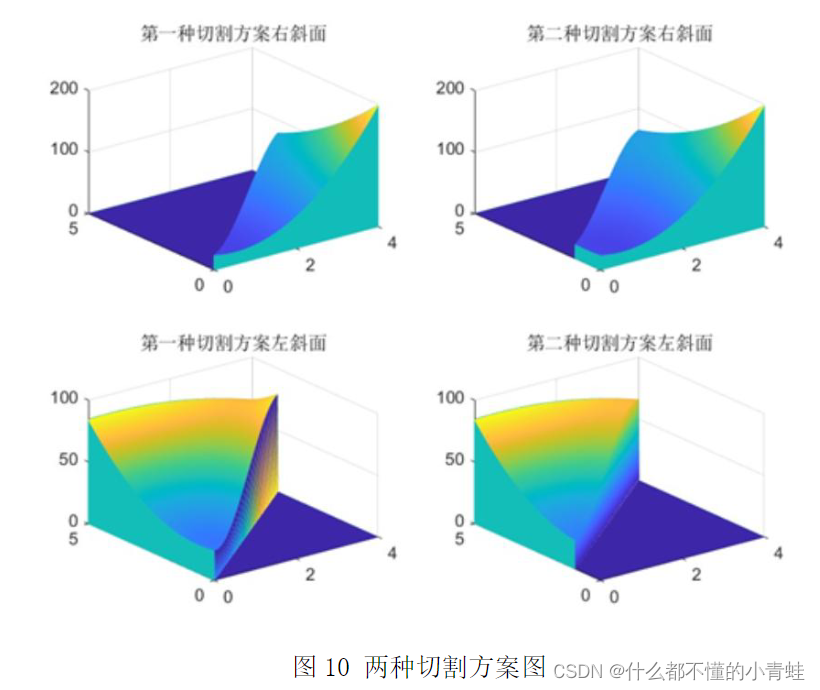
subplot(3,2,3);
z1=triu(z);
meshz(X,Y,z1)
6
subplot(3,2,4);
z2=triu(z,-50);
meshz(X,Y,z2)
subplot(3,2,5);
z3=tril(z);
meshz(X,Y,z3)
subplot(3,2,6);
z4=tril(z,-50);
meshz(X,Y,z4)
shading interp
相关文章:

数模国赛——多波束测线问题模型建立研究分析
第一次参加数模国赛,太菜了~~~~意难平 问题一 画出与测线方向垂直的平面和海底坡面的交线构成一条与水平面夹角为𝐀的斜线的情况下的示意图进行分析,将覆盖宽度分为左覆盖宽度和右覆盖宽度,求出它们与海水深度和𝐀、…...
)
[AUTOSAR][诊断管理][ECU][$37] 请求退出传输。终止数据传输的(上传/下载)
文章目录 一、简介二、服务请求报文定义肯定响应支持的NRC三、示例流程Step 1:Step 2:报文示例:Step 1:请求RequestDownload(0x34)服务Step 2:请求TransferData (0x36)服务,传输数据Step 3:请求RequestTransferExit(0x37)服务总结:三、示例代码37_req_transfer_e…...

vue+canvas实现横跨整个页面的动态的波浪线(贝塞尔曲线)
本来写这个特效 我打算用css实现的,结果是一波三折,我太难了,最终没能用css实现,转战了canvas来实现。来吧先看效果图 当然这个图的波浪高度、频率、位置、速度都是可调的,请根据自己的需求调整,如果你讲波浪什么的调大一下 还有有摆动的效果哦。 以下是完整代码 <…...
LeetCode算法题解| 669. 修剪二叉搜索树、108. 将有序数组转换为二叉搜索树、538. 把二叉搜索树转换为累加树
一、LeetCode 669. 修剪二叉搜索树 题目链接:669. 修剪二叉搜索树 题目描述: 给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变…...

直播界很火的无线领夹麦克风快充方案 Type-C接口 PD快充+无线麦克风可同时进行
当前市场上流行一款很火的直播神器,无线领夹麦克风(MIC),应用于网红直播,网课教学,采访录音,视频录制,视频会议等等场景。 麦克风对我们来说并不陌生,而且品类有很多。随…...
Jmeter 汉化中文语言
找到 bin -> jmeter.propertise 修改参数:languageen --> languagazh_CN OK!...
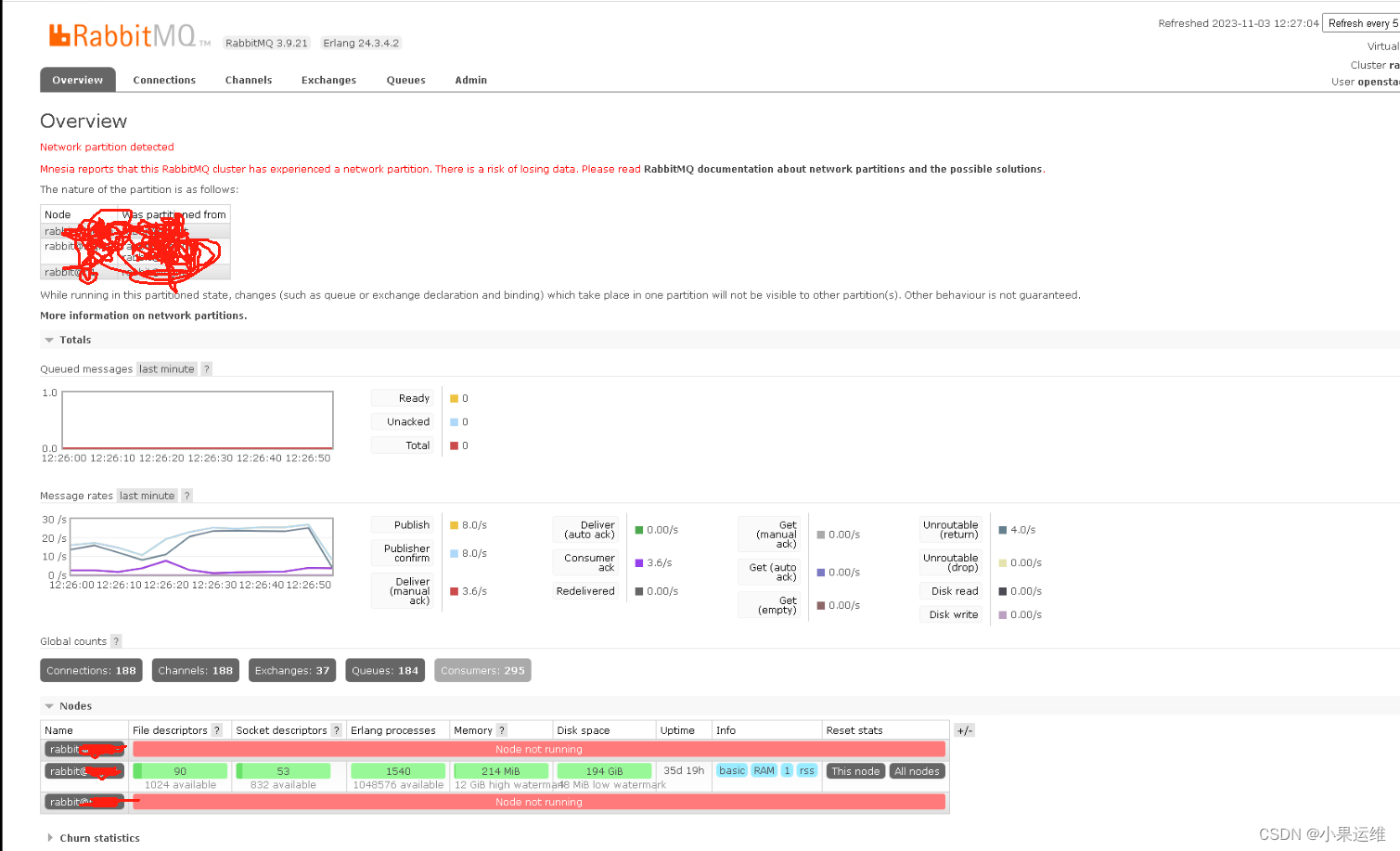
centos9 stream 下 rabbitmq高可用集群搭建及使用
RabbitMQ是一种常用的消息队列系统,可以快速搭建一个高可用的集群环境,以提高系统的弹性和可靠性。下面是搭建RabbitMQ集群的步骤: 基于centos9 stream系统 1. 安装Erlang和RabbitMQ 首先需要在所有节点上安装Erlang和RabbitMQ。建议使用官…...

代码随想录算法训练营第10天|232. 用栈实现队列 225. 用队列实现栈
JAVA代码编写 232. 用栈实现队列 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除…...

线上Kafka集群如何调整消息存储时间
这里是weihubeats,觉得文章不错可以关注公众号小奏技术,文章首发。拒绝营销号,拒绝标题党 Kafka版本 kafka_2.13-3.5.0 背景 Kafka 默认消息存储时间为7天,实际线上的业务使用Kafka更多的是一些数据统计之类的业务,大多是朝生夕…...
[迁移学习]DA-DETR基于信息融合的自适应检测模型
原文标题为:DA-DETR: Domain Adaptive Detection Transformer with Information Fusion;发表于CVPR2023 一、概述 本文所描述的模型基于DETR,DETR网络是一种基于Transformer的目标检测网络,详细原理可以参见往期文章:…...
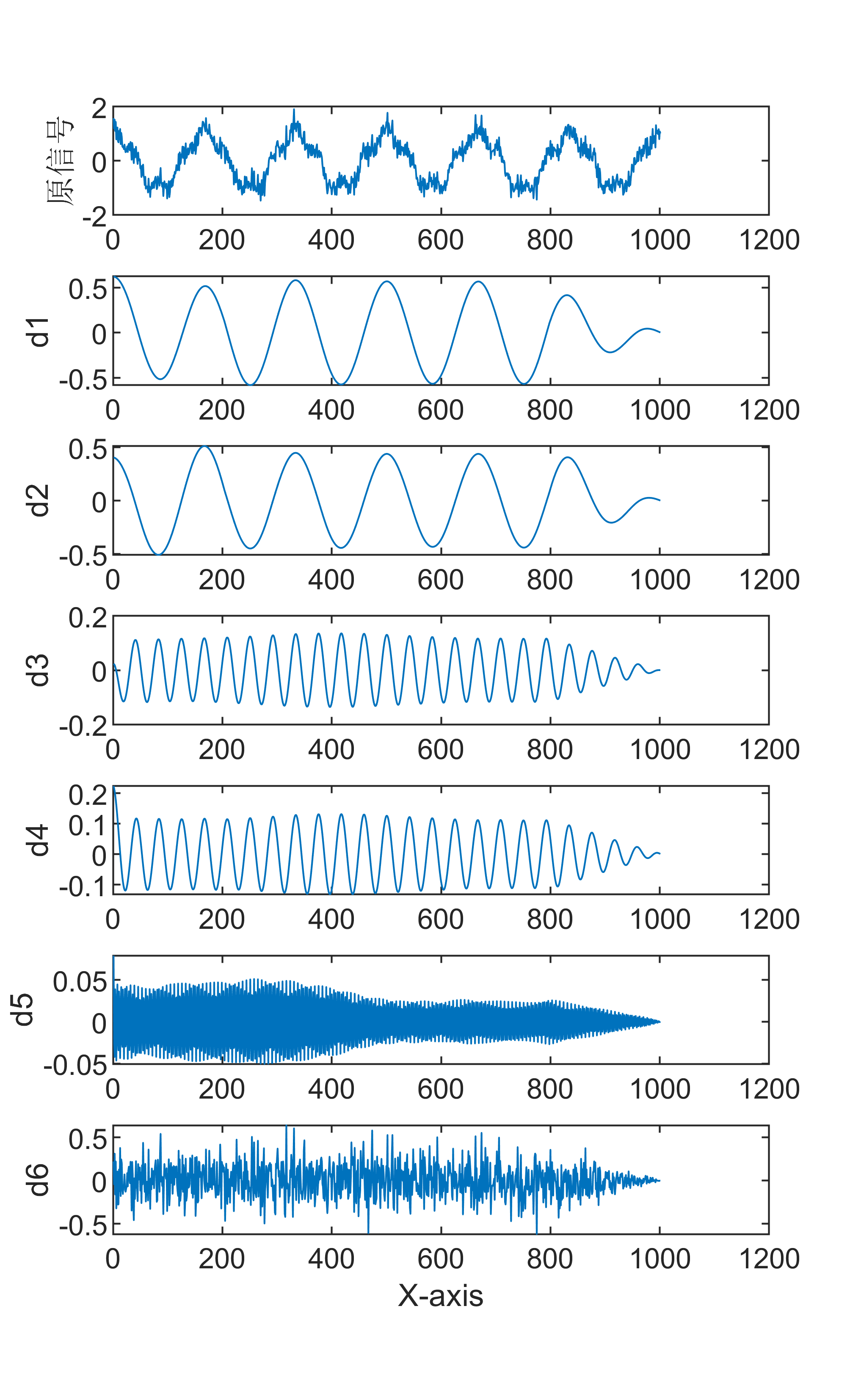
【MATLAB】全网唯一的13种信号分解+FFT傅里叶频谱变换联合算法全家桶
有意向获取代码,请转文末观看代码获取方式~ 大家吃一顿火锅的价格便可以拥有13种信号分解FFT傅里叶频谱变换联合算法,绝对不亏,知识付费是现今时代的趋势,而且都是我精心制作的教程,有问题可随时反馈~也可单独获取某一…...
Nginx安装与配置
1.下载安装包 官网下载地址:nginx: download 可以先将安装包下载到本地再传到服务器,或者直接用wget命令将安装包下载到服务器,这里我们直接将安装包下载到服务器上。未安装wget命令的需要先安装wget,yum install -y wget [root…...

linux笔记总结-基本命令
参考: 1.Linux 和Windows比 比较 (了解) 1. 记住一句经典的话:在 Linux 世界里,一切皆文件 2. Linux目录结构 /lib • 系统开机所需要最基本的动态连接共享库,其作用类似于Windows里的DLL文件。几 乎所有…...
[PHP]禅道项目管理软件ZenTaoPMS源码包 v16.4
禅道项目管理软件ZenTaoPMS一键安装包是一款国产的开源项目管理软件。它集产品管理、项目管理、质量管理、文档管理、组织管理和事务管理于一体,是一款专业的研发项目管理软件,完整地覆盖了项目管理的核心流程。注重实效的管理思想,合理的软件…...

Required String parameter ‘name‘ is not present
[org.springframework.web.bind.MissingServletRequestParameterException: Required String parameter name is not present] 服务端有参数name,客户端没有传上来...
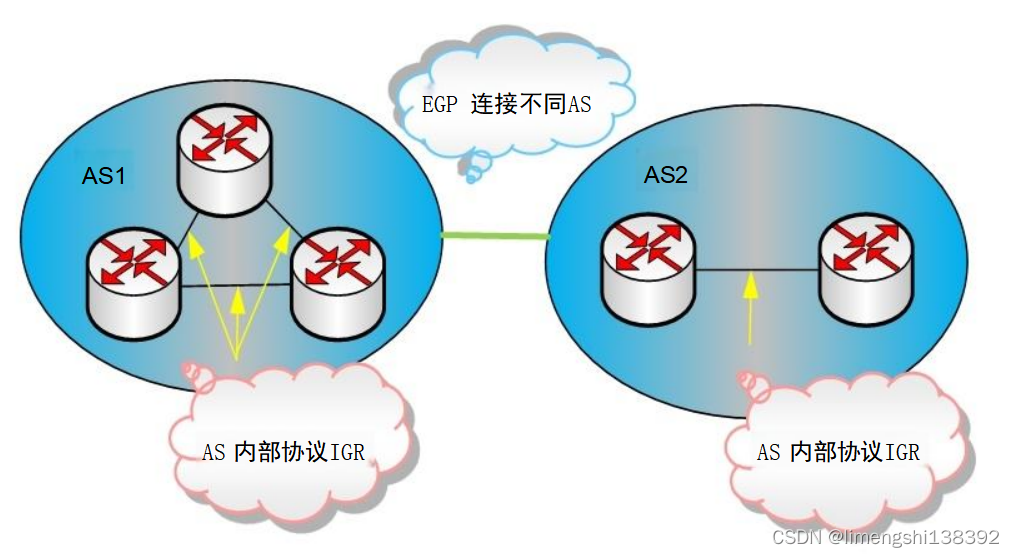
路由器基础(五): OSPF原理与配置
开放式最短路径优先 (Open Shortest Path First,OSPF) 是一个内部网关协议 (Interior Gateway Protocol,IGP),用于在单一自治系统(Autonomous System,AS) 内决策路由。OSPF 适合小型、中型、较大规模网络。OSPF 采用Dijkstra的最短路径优先算法 (Shortest Pat…...
Leetcode1128. 等价多米诺骨牌对的数量
Every day a Leetcode 题目来源:1128. 等价多米诺骨牌对的数量 解法1:暴力 代码: class Solution { public:int numEquivDominoPairs(vector<vector<int>> &dominoes){int n dominoes.size(), count 0;for (int i 0;…...
Dev-C调试的基本方法2-2
3.3 跳出函数 在图6所示的状态下,点击单步调试(F7)会继续调试下一行,而如果想结束在函数中的调试,则点击图4③所示的跳出函数,或CtrlF8按键跳出f()函数,程序将会停在图5所示的第11行处。 3.4 …...

企业之间的竞争,ISO三体系认证至关重要!
ISO三体系认证是指ISO 9001质量管理体系认证、ISO 14001环境管理体系认证、ISO 45001(OHSAS18001)职业健康安全管理体系认证。企业(组织)自愿申请、通过ISO三体系认证,并贯彻落实,确实能获益多多。 ISO 9001质量管理体系 我们经…...
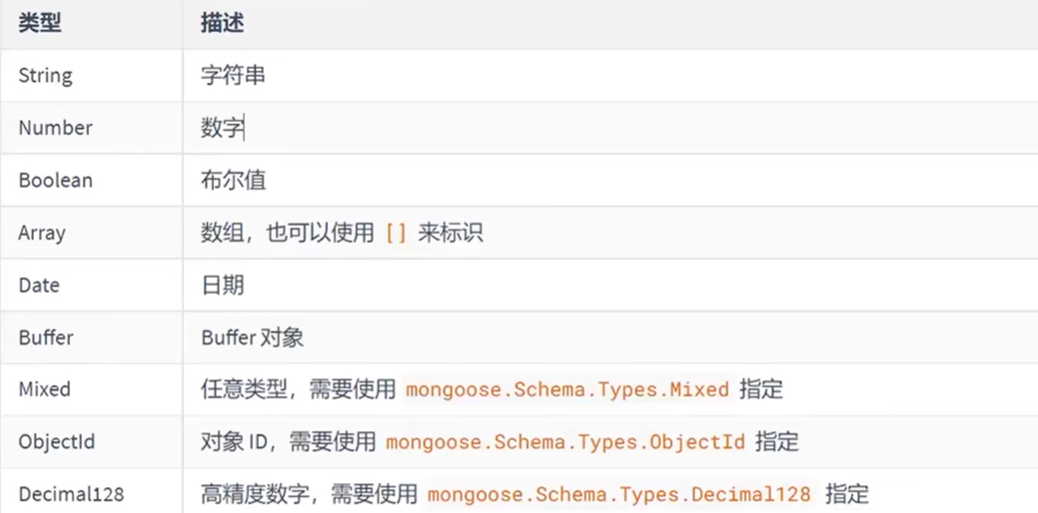
node教程(四)Mongodb+mongoose
文章目录 一、mongodb1.简介1.1Mongodb是什么?1.2数据库是什么?1.3数据库的作用1.4数据库管理数据的特点 2.核心概念3.下载安装与启动4.命令行交互4.1数据库命令4.3文档命令 二、Mongoose1.介绍2.作用3.使用流程4.插入文档5.mongoose字段类型 一、mongod…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
