NOIP2023模拟10联测31 涂鸦
题目大意
有一面由 n × m n\times m n×m个格子组成的墙,每个格子要么是黑色,要么是白色。你每次将会进行这样的操作:等概率随机选择一个位置 ( x , y ) (x,y) (x,y)和一个颜色 c c c(黑色或白色),( 1 ≤ x ≤ n , 1 ≤ y ≤ m 1\leq x\leq n,1\leq y\leq m 1≤x≤n,1≤y≤m,选择任意 ( x , y , c ) (x,y,c) (x,y,c)的组合的概率都是 1 2 n m \dfrac{1}{2nm} 2nm1),然后将 ( x , y ) (x,y) (x,y)左上角的所有格子的颜色都涂成 c c c,也就是将所有满足 1 ≤ x ′ ≤ x , 1 ≤ y ′ ≤ y 1\leq x'\leq x,1\leq y'\leq y 1≤x′≤x,1≤y′≤y的格子 ( x ′ , y ′ ) (x',y') (x′,y′)的颜色涂成 c c c。次操作的代价为涂的格子的数量,即 x × y x\times y x×y。给定初始状态和终止状态,问期望要花费多少代价才能将墙面从初始状态涂成终止状态。
1 ≤ n , m ≤ 5 1\leq n,m\leq 5 1≤n,m≤5
题解
看到 n n n和 m m m都比较小,我们考虑用状压 D P DP DP。设 f s f_s fs表示当前墙面的状态为 s s s时要到最终状态的期望代价,可以列出 2 n m 2^{nm} 2nm个方程,用高斯消元解方程即可。
这样做的时间复杂度为 O ( 2 3 n m ) O(2^{3nm}) O(23nm),我们考虑优化。
我们考虑减少状态的数量。我们发现,如果一个位置的右下角的某个位置与最终状态不同,则这个位置一定会被修改,那这个位置当前的值就不重要了。
设 p i , j p_{i,j} pi,j表示 ( i , j ) (i,j) (i,j)右下角的位置是否已经全部变得和终止状态一样,可以发现 p i , j p_{i,j} pi,j为 1 1 1的状态一定在右下角呈阶梯状的。举个例子:

其中橙色部分为 p i , j = 1 p_{i,j}=1 pi,j=1的格子。
那么,总状态数为 ( n + m n ) \binom{n+m}{n} (nn+m)。我们可以用 d f s dfs dfs求出所有可能的状态。
对于每个状态,我们考虑它能到达哪些状态。我们将每种状态中 p i , j = 1 p_{i,j}=1 pi,j=1的格子设为与终止状态相同, p i , j = 0 p_{i,j}=0 pi,j=0的格子设为与终止状态相反。然后将左上角的一个矩形全部变为黑色或白色,再判断改变颜色后的状态是什么状态。
用上述方法求出转移方程,再用高斯消元求解即可。
时间复杂度为 O ( ( n + m n ) 3 ) O(\binom{n+m}{n}^3) O((nn+m)3), ( n + m n ) \binom{n+m}{n} (nn+m)的最大值为 252 252 252,是可以过的。
code
#include<bits/stdc++.h>
using namespace std;
const long long mod=998244353;
int n,m,S,bg=0,ed=0,sum=0,tot=0,w[10][10];
long long ans=0,a[305][305];
char s[10][10],t[10][10];
array<int,5>v;
map<array<int,5>,int>mp;
void init(){S=(1<<n*m)-1;for(int i=0;i<n;i++){for(int j=0;j<m;j++){for(int x=0;x<=i;x++){for(int y=0;y<=j;y++){w[i][j]|=1<<(x*m+y);}}}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){sum+=2*i*j;}}
}
void dfs(int t,int now){if(t==n){mp[v]=++tot;return;}for(int i=now;i<=m;i++){v[t]=i;dfs(t+1,i);}
}
int gtid(int s){array<int,5>b;for(int i=0;i<5;i++) b[i]=0;for(int i=0;i<n;i++){b[i]=m;for(int j=0;j<m;j++){int wt=(s>>(i*m+j))&1;if(wt==(t[i][j]=='W')) b[i]=m-j-1;}}for(int i=n-2;i>=0;i--) b[i]=min(b[i],b[i+1]);return mp[b];
}
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void gauss(){for(int i=1;i<=tot;i++){for(int j=i;j<=tot;j++){if(a[j][i]){swap(a[j],a[i]);break;}}for(int j=1;j<=tot;j++){if(i==j) continue;long long dv=(mod-1)*a[j][i]%mod*mi(a[i][i],mod-2)%mod;for(int k=1;k<=tot+1;k++) a[j][k]=(a[j][k]+dv*a[i][k])%mod;}}
}
int main()
{
// freopen("graffiti.in","r",stdin);
// freopen("graffiti.out","w",stdout);scanf("%d%d",&n,&m);init();for(int i=0;i<n;i++) scanf("%s",s[i]);for(int i=0;i<n;i++) scanf("%s",t[i]);for(int i=0;i<n;i++){for(int j=0;j<m;j++){bg|=(s[i][j]=='B')<<(i*m+j);ed|=(t[i][j]=='B')<<(i*m+j);}}dfs(0,0);for(auto p:mp){int s=0,id=p.second;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(j<m-p.first[i])s|=(t[i][j]=='W')<<(i*m+j);elses|=(t[i][j]=='B')<<(i*m+j);}}a[id][id]=2*n*m;if(s==ed) continue;a[id][tot+1]=sum;for(int i=0;i<n;i++){for(int j=0;j<m;j++){int tmp=gtid(s|w[i][j]);a[id][tmp]=(a[id][tmp]-1+mod)%mod;tmp=gtid(s&(S^w[i][j]));a[id][tmp]=(a[id][tmp]-1+mod)%mod;}}}gauss();int tmp=gtid(bg);ans=a[tmp][tot+1]*mi(a[tmp][tmp],mod-2)%mod;printf("%lld",ans);return 0;
}
相关文章:

NOIP2023模拟10联测31 涂鸦
题目大意 有一面由 n m n\times m nm个格子组成的墙,每个格子要么是黑色,要么是白色。你每次将会进行这样的操作:等概率随机选择一个位置 ( x , y ) (x,y) (x,y)和一个颜色 c c c(黑色或白色),࿰…...
【Python基础知识一】基本语法、常用数据类型等
Python基础知识: 1 标识符(Identifier)2 关键字/保留字(Keyword)3 引号4 编码5 输入输出6 行与缩进7 多行语句8 注释9 数据类型9.1 数字(Number)类型9.2 变量(variate)9.3 字符串(St…...

听听ChatGPT对IT行业的发展和就业前景的看法
🌈个人主页: Aileen_0v0🔥系列专栏:PYTHON学习系列专栏💫"没有罗马,那就自己创造罗马~" 目录 (1)判断素数 写法1: 写法2: (2)计算1-100的偶数之和 写法1: 写法2: (3)计算1-100的奇数之和 (4)多层循环 IT行业哪个方向比较…...

〖程序员的自我修养 - 认知剖析篇⑤〗- 选择前端还是后端?
人之所以会觉得迷茫,本质上是欠缺对自己的一个控制力、识别庞杂信息、去伪存真的独立思考与认知能力。 说明:该文属于 程序员的自我修养 专栏,购买任意白宝书体系化专栏可加入易编程社区,早鸟价订阅模式除外。福利:加入社区的小伙伴们,除了可以获取博主所有付费专栏的阅读…...

Rust语言初步
文章目录 安装与测试变量条件语句和函数数组和元组循环 安装与测试 可以从官网直接下载。下载rustup-init并运行之后,会打开命令行,选1默认安装,然后不出意外就安装完了。 安装完成后按照惯例查看一下版本,如不报错就算成功。 …...

BIMILLC算法源码解析
论文链接:https://arxiv.org/abs/1607.02533 源码出处:https://github.com/Harry24k/adversarial-attacks-pytorch/tree/master 源码 import torch import torch.nn as nnfrom ..attack import Attackclass BIM(Attack):r"""BIM or iter…...

Android STR研究之五
前言: 在前四篇中初步介绍了开机流程,STR流程,唤醒流程,这里讲下STR的问题点 Android STR研究之一-CSDN博客 Android STR研究之二-CSDN博客 Android STR研究之三-CSDN博客 Android STR研究之四-CSDN博客 问题1:进入STR…...

python3+requests接口自动化测试实例详细操作
前段时间由于公司测试方向的转型,由原来的web页面功能测试转变成接口测试,之前大多都是手工进行,利用postman和jmeter进行的接口测试,后来,组内有人讲原先web自动化的测试框架移驾成接口的自动化框架,使用的…...

在Node.js中,什么是中间件(middleware)?它们的作用是什么?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

当函数参数为一级指针,二级指针
当函数参数为一级指针,二级指针 在讲述内容之前,先讲四点重要知识 1.当传入参数时,函数形参会立即申请形参的内存空间,函数执行完毕后,形参的内存空间立即释放掉。 1.指针是存放其他变量地址的变量。指针有自己的内…...

Hydra post登录框爆破
文章目录 无token时的Hydra post登录框爆破带Token时的Hydra post登录框爆破 无token时的Hydra post登录框爆破 登录一个无验证码和token的页面,同时抓包拦截 取出发送数据包:usernameadb&password133&submitLogin 将用户名和密码替换 userna…...
阿里云推出AI编程工具“通义灵码“;生成式 AI 入门教程 2
🦉 AI新闻 🚀 阿里云推出AI编程工具"通义灵码",支持多种语言及实时续写功能 摘要:阿里云推出了一款名为"通义灵码"的AI编程工具,支持多种主流编程语言,包括Java、Python、Go等。该工…...
使用Qt Installer Framework将自己的程序打包成安装包程序
使用Qt Installer Framework将自己的程序打包成安装包程序 制作安装包程序就是将自己的程序打包成一个可执行的exe,双击之后进行安装。 1. 在制作安装包程序之前需要安装qt官方提供的安装包制作工具Qt Installer Framework 去qt官方网址,下载对应的 Q…...

逆袭Flutter? Facebook 发布全新跨平台引擎 Hermes!
Facebook 于前日发布了新的 JavaScript 引擎:Hermes,专注于提高 React Native 应用的性能,并且在市面上那些内存较少、存储速度较慢且计算能力低下的移动设备上都有良好的表现。但是不是为了追赶Flutter?这块作者没有说明。 移动应…...

c++ 互斥锁使用详解 lock_guard
c 互斥锁使用详解 std::mutex 用于保护共享资源,防止多个线程同时修改共享资源而引发竞争条件。 成员函数 lock:锁定互斥,若互斥不可用则阻塞。try_lock:尝试锁定互斥,若互斥不可用则返回。unlock:解锁…...
【快速解决】Android Button页面跳转功能
目录 让我们直接开始 第一步:先建立一个新的activity 编辑 第二步:打开第一个页面的Java文件MainActivity 方法一:直接跳转功能如下: 方法二:输入密码才能进行跳转功能如下: 需要注意的地方 结语 让…...

C语言 pthread_create
备注void *,最好添加返回值 原因:在实践中,虽然你的函数可能不需要返回任何值,但为了与 pthread_create 函数的预期函数指针格式相匹配,最好遵守函数指针所需的返回类型。这是一种良好的编程实践,确保你的代…...

前端uniapp提交表单调用接口方法最新
目录 源码1源码2最后 源码1 <template><view class"my-add-bank-card"><!-- name"bank_name" form表单提交的input里面一定要加name绑定要传的参数 name"bank_name" type"text" v-model"address.bank_name"…...

OpenFeign的简单介绍和功能实操
前言 本文主要做一下OpenFeign的简单介绍和功能实操,实操主要是OpenFeign的超时和重试,在阅读本文章前,请完成《Nacos 注册中心介绍与实操》内的Nacos多模块生产消费者项目 什么是OpenFeign OpenFeign全名Spring Cloud OpenFeignÿ…...

webpack 高级
高级配置就是要进行 webpack 优化,让代码在编译、运行时性能更好 主要从以下角度去优化: 1、提升开发体验 2、提升打包构建速度 3、减少代码体积 4、优化代码运行性能 一、提升体验 1、SourceMap 为什么 打包出来的所有css和js合并成了一个文件&#…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...
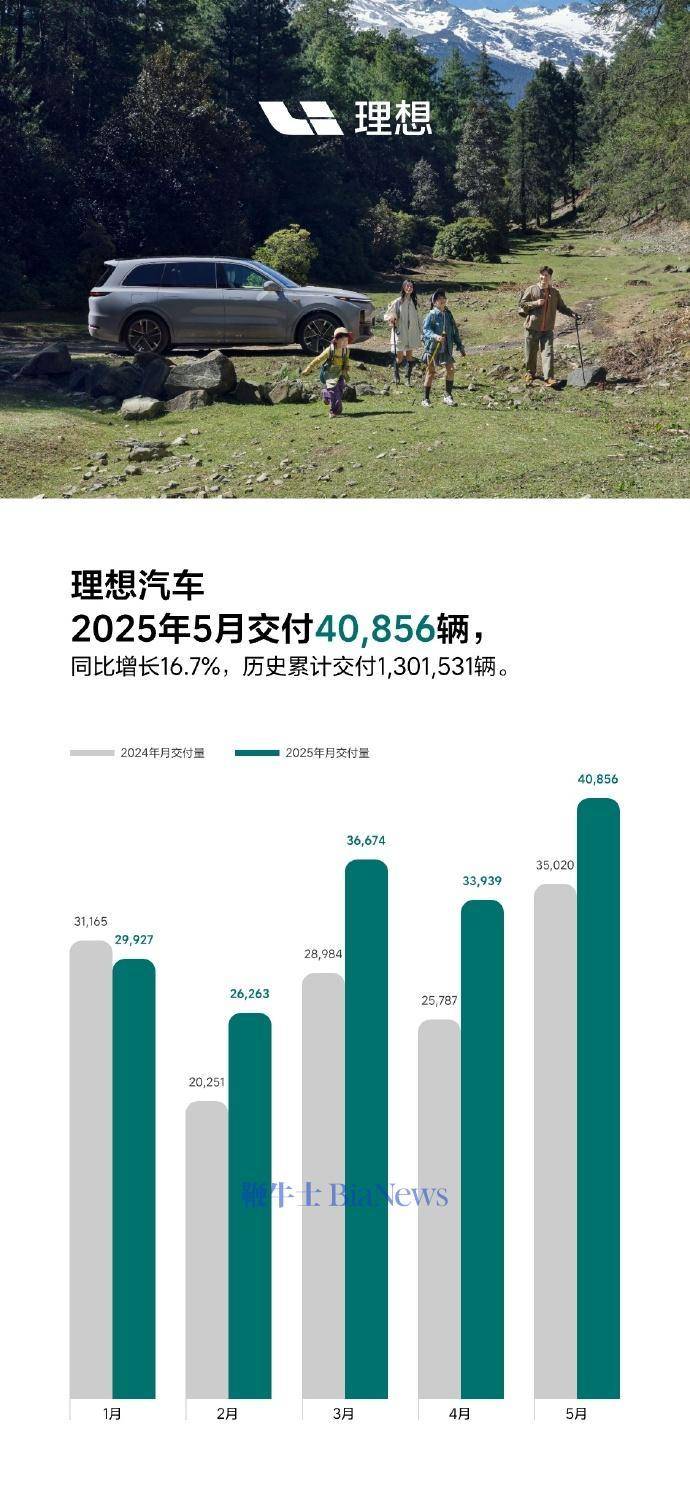
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
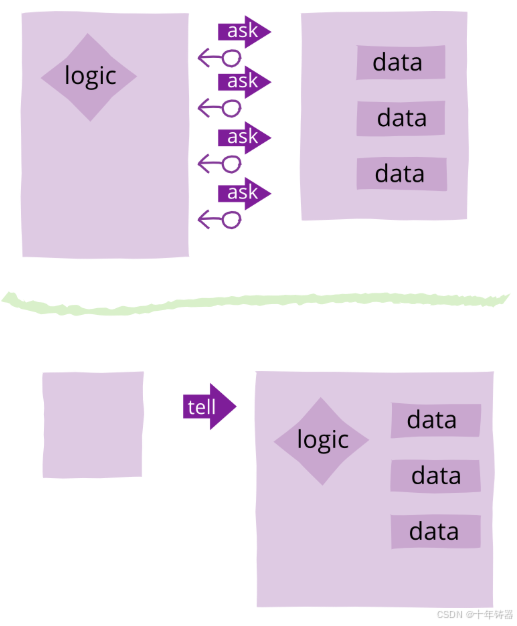
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...
