力扣第322题 零钱兑换 c++ java 动态规划
题目
322. 零钱兑换
中等
相关标签
广度优先搜索 数组 动态规划
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11输出:3解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3输出:-1
示例 3:
输入:coins = [1], amount = 0 输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
思路和解题方法
目标和的定义:这个问题的目标是计算凑出目标金额所需的最少硬币数量。
动态规划的思路:该代码使用了动态规划的思想,将原问题拆解为子问题,并利用已解决的子问题的解来求解更大规模的问题。
dp数组的定义:代码创建了一个大小为amount+1的dp数组,用于保存计算中间状态的结果。dp[i]表示组成金额i所需的最少硬币数量。初始化:将
dp[0]初始化为 0,表示组成金额为 0 不需要任何硬币。其他位置的dp数组元素初始化为INT_MAX,表示初始时无法凑出对应的金额。状态转移方程:采用两层循环来遍历物品和背包。外层循环遍历所有可用的硬币面额,内层循环遍历目标金额从该硬币面额开始到
amount。这样可以逐步更新dp数组,计算得到凑出每个目标金额所需的最少硬币数量。状态转移:对于当前的目标金额
j,我们检查dp[j - coins[i]]是否不是初始值INT_MAX。如果不是初始值,则表示可以通过使用当前硬币面额coins[i]得到目标金额j。我们比较使用当前硬币和不使用当前硬币两种情况下所需的硬币数量,并取最小值作为dp[j]的解。返回结果:最后,我们返回
dp[amount]的值作为结果。如果dp[amount]仍为初始值INT_MAX,表示无法凑出目标金额,因此返回 -1。总结起来,这段代码使用动态规划的思想,通过构建一个
dp数组来保存计算中间状态的结果。通过遍历物品和背包,并利用已解决子问题的解,逐步计算得到组成目标金额所需的最少硬币数量。最终,返回dp[amount]的值作为结果。
复杂度
时间复杂度:
O(n * amount)
时间复杂度:
- 外层循环遍历硬币列表的长度,即
coins的大小,所以时间复杂度为 O(n),其中 n 是硬币列表的长度。- 内层循环遍历目标金额
amount,所以时间复杂度为 O(amount)。综合起来,总的时间复杂度为 O(n * amount)。
空间复杂度
O(amount)
空间复杂度:
- 创建了一个大小为
amount+1的dp数组,所以空间复杂度为 O(amount)。因此,该算法的空间复杂度为 O(amount)。
c++ 代码
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX); // 创建大小为 amount+1 的 dp 数组,初始值设置为 INT_MAXdp[0] = 0; // 对于组成金额为 0 的情况,方法数为 0for (int i = 0; i < coins.size(); i++) { // 遍历每个硬币面额(物品)for (int j = coins[i]; j <= amount; j++) { // 遍历每个目标金额(背包)if (dp[j - coins[i]] != INT_MAX) { // 如果 dp[j - coins[i]] 不是初始值(即存在组合方式)dp[j] = min(dp[j - coins[i]] + 1, dp[j]); // 更新组成金额 j 的最小方法数}}}if (dp[amount] == INT_MAX) return -1; // 如果无法组成金额 amount,则返回 -1 表示无解return dp[amount]; // 返回组成金额 amount 的最小方法数}
};
vector<int> dp(amount + 1, INT_MAX);:创建大小为 amount+1 的 dp 数组,用于保存组成不同金额的最小硬币数。初始值设置为 INT_MAX,表示初始状态下无解。dp[0] = 0;:对于金额为 0 的情况,不需要使用任何硬币,所以最小硬币数为 0。for (int i = 0; i < coins.size(); i++):外层循环遍历硬币面额(物品),以便逐个考虑每个硬币的组合方式。for (int j = coins[i]; j <= amount; j++):内层循环遍历目标金额(背包),从当前硬币面额开始,直到目标金额 amount。这样可以确保只考虑能够达到的金额。if (dp[j - coins[i]] != INT_MAX):如果 dp[j - coins[i]] 不是初始值(即存在组合方式),则进入条件判断。dp[j] = min(dp[j - coins[i]] + 1, dp[j]);:更新组成金额 j 的最小硬币数。在当前硬币面额 coins[i] 的情况下,组成金额 j 的最小硬币数为 dp[j - coins[i]] + 1 和当前 dp[j] 的较小值。if (dp[amount] == INT_MAX) return -1;:如果无法组成金额 amount,则返回 -1 表示无解。return dp[amount];:返回组成金额 amount 的最小硬币数。
Java代码
class Solution {public int coinChange(int[] coins, int amount) {int max = Integer.MAX_VALUE;int[] dp = new int[amount + 1];//初始化dp数组为最大值for (int j = 0; j < dp.length; j++) {dp[j] = max;}//当金额为0时需要的硬币数目为0dp[0] = 0;for (int i = 0; i < coins.length; i++) {//正序遍历:完全背包每个硬币可以选择多次for (int j = coins[i]; j <= amount; j++) {//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要if (dp[j - coins[i]] != max) {//选择硬币数目最小的情况dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == max ? -1 : dp[amount];}
}觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第322题 零钱兑换 c++ java 动态规划
题目 322. 零钱兑换 中等 相关标签 广度优先搜索 数组 动态规划 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组…...

uniapp 子组件内使用定时器无法清除
涉及到的知识点:1.ref绑定在组建上获取组件实例。2.emit逆向传值,不需要点击触发,watch监听即可。 需求:在父页面的子组件定时发送请求,离开父页面就停止,再次进入就开启。 问题:在父页面的子…...

加载动态库的几种方式
静态加载、动态加载和延迟加载 dll加载方式大致可以分为3类:静态加载、动态加载和延迟加载 1.静态加载,dll的加载发生在程序main函数启动前。 2.动态加载,使用LoadLibrary或者LoadLibraryEx来加载一个dll。当dll加载成功时,你会…...

视频转序列图片:掌握技巧,轻松转换
随着社交媒体和视频平台的日益普及,视频已成为我们生活中不可或缺的一部分。有时,我们需要将视频转换为图片序列,例如制作GIF动图或提取视频中的特定画面。现在一起来看云炫AI智剪如何将视频转换为序列图片,并轻松实现转换。 操作…...
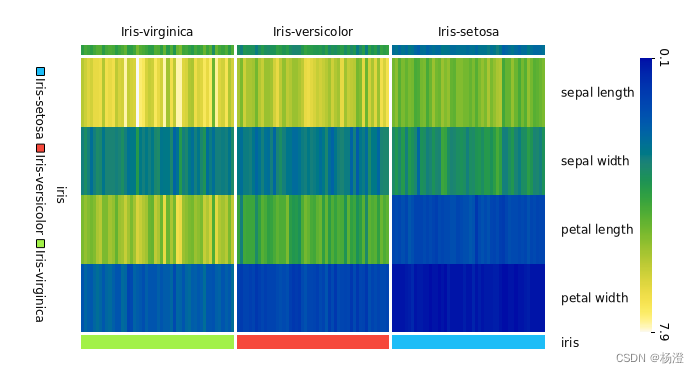
python 数据挖掘库orange3 介绍
orange3 是一个非常适合初学者的data mining library. 它让使用者通过拖拽内置的组件来形成工作流。让你不需要写任何代码就可以体验到数据挖掘和可视化的魅力。 它的桌面如下,这里我创建了 3 个节点,分别是数据集、小提琴图,散点图 其中 …...
Android和JNI交互 : 常见的图像格式转换 : NV21、RGBA、Bitmap等
1. 前言 最近在使用OpenCV处理图片的时候,经常会遇到需要转换图像的情况,网上相关资料比较少,也不全,有时候得费劲老半天才能搞定。 自己踩了坑后,在这里记录下,都是我在项目中遇到的图像转化操作…...

AndroidAuto 解决连接手机启动AA屏闪一下问题
AndroidAuto一般在AndroidManifest.xml注册的Activity配置过滤监听特定手机的USB插拔启动AA <activityandroid:name=".sink.ui.MainActivity"android:configChanges="keyboard|keyboardHidden|uiMode"android:windowSoftInputMode="stateHidden&qu…...
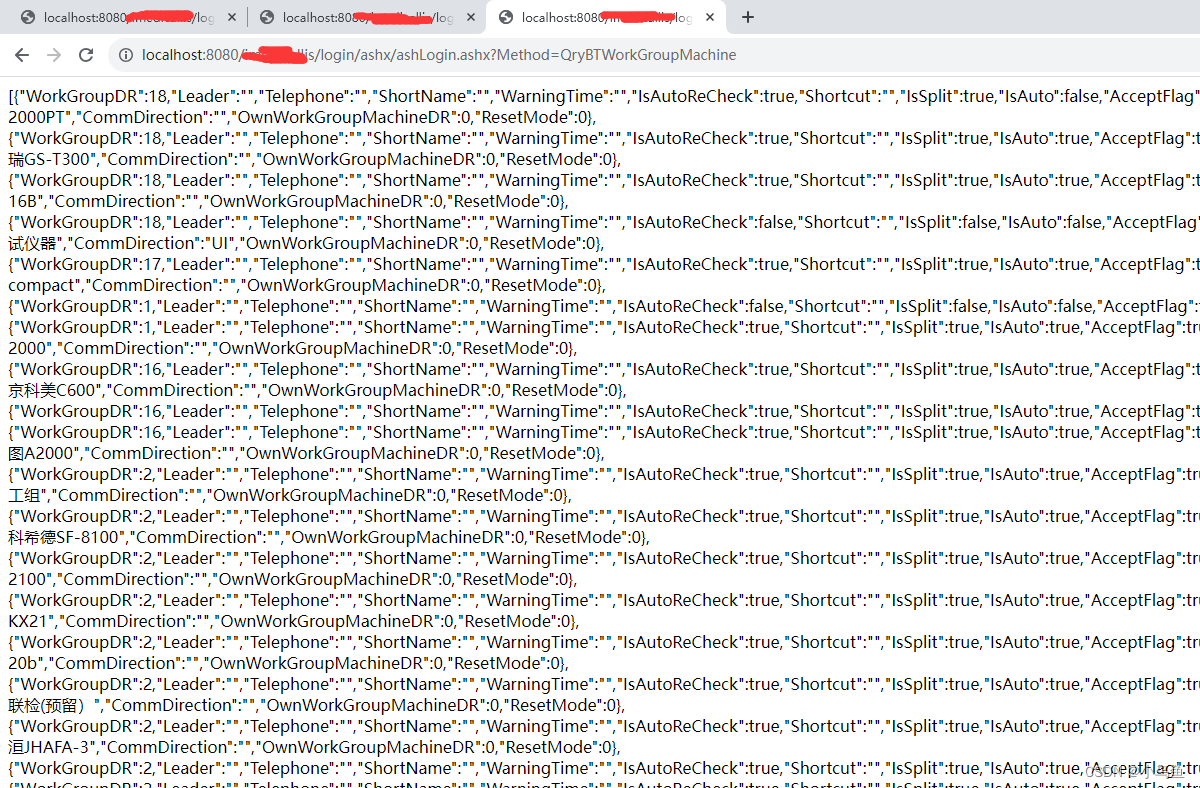
jbase实现业务脚本化
经过晚上和早上的努力,终于补上框架最后一块了,业务脚本侦听变化后自动编译jar包和调用,实现维护成本低,开发效率高的框架的基本体系。 实现自动编译jar包的类 package appcode;import org.w3c.dom.Document; import org.w3c.do…...

【安全】Java幂等性校验解决重复点击(6种实现方式)
目录 一、简介1.1 什么是幂等?1.2 为什么需要幂等性?1.3 接口超时,应该如何处理?1.4 幂等性对系统的影响 二、Restful API 接口的幂等性三、实现方式3.1 数据库层面,主键/唯一索引冲突3.2 数据库层面,乐观锁…...
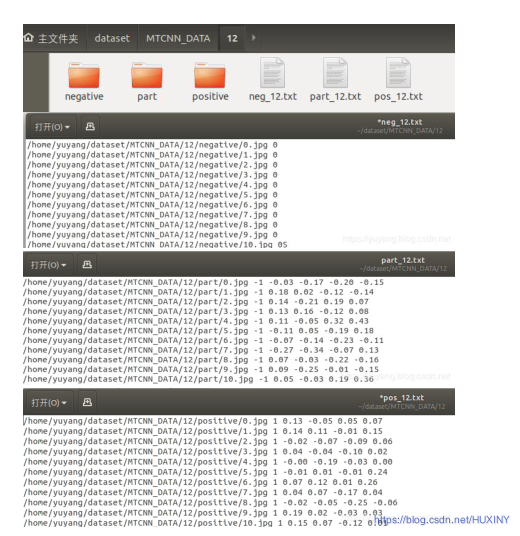
基于设深度学习的人脸性别年龄识别系统 计算机竞赛
文章目录 0 前言1 课题描述2 实现效果3 算法实现原理3.1 数据集3.2 深度学习识别算法3.3 特征提取主干网络3.4 总体实现流程 4 具体实现4.1 预训练数据格式4.2 部分实现代码 5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习机器视觉的…...

0001Java安卓程序设计-基于Android多餐厅点餐桌号后厨前台服务设计与开发
文章目录 **摘** **要****目** **录**系统设计开发环境 编程技术交流、源码分享、模板分享、网课教程 🐧裙:776871563 摘 要 移动互联网时代的到来,给人们的生活带来了许多便捷和乐趣。随着用户的不断增多,其规模越来越大&#…...
Node.js 中解析 HTML 的方法介绍
在 Web 开发中,解析 HTML 是一个常见的任务,特别是当我们需要从网页中提取数据或操作 DOM 时。掌握 Node.js 中解析 HTML 的各种方式,可以大大提高我们提取和处理网页数据的效率。本文将介绍如何在 Node.js 中解析 HTML。 基本概念 HTML 解析…...

软件开发项目文档系列之十如何撰写测试用例
目录 1 概述1.1 编写目的1.2 定义1.3 使用范围1.4 参考资料1.5 术语定义 2 测试用例2.1 功能测试2.1.1 用户登录功能2.1.2 商品搜索功能 2.2 性能测试2.2.1 网站响应时间2.2.2 并发用户测试 附件: 测试用例撰写的要素和注意事项附件1 测试用例要素附件2 测试用例的注…...

AI:53-基于机器学习的字母识别
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌本专栏包含以下学习方向: 机器学习、深度学…...
实习记录--(海量数据如何判重?)--每天都要保持学习状态和专注的状态啊!!!---你的未来值得你去奋斗
海量数据如何判重? 判断一个值是否存在?解决方法: 1.使用哈希表: 可以将数据进行哈希操作,将数据存储在相应的桶中。 查询时,根据哈希值定位到对应的桶,然后在桶内进行查找。这种方法的时间复…...
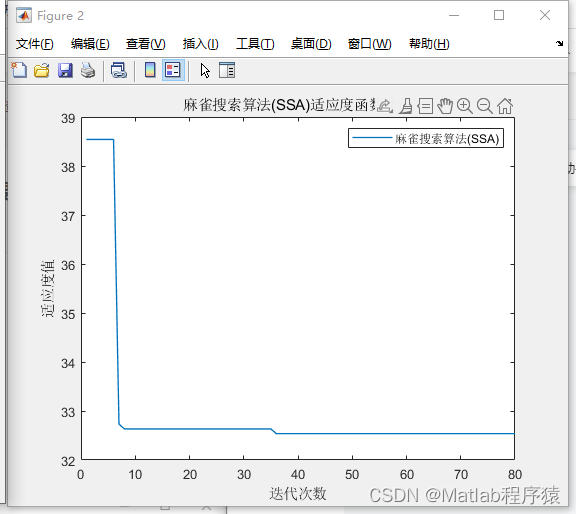
【MATLAB源码-第67期】基于麻雀搜索算法(SSA)的无人机三维地图路径规划,输出最短路径和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 麻雀搜索算法(Sparrow Search Algorithm, SSA)是一种新颖的元启发式优化算法,它受到麻雀社会行为的启发。这种算法通过模拟麻雀的食物搜索行为和逃避天敌的策略来解决优化问题。SSA通过模…...
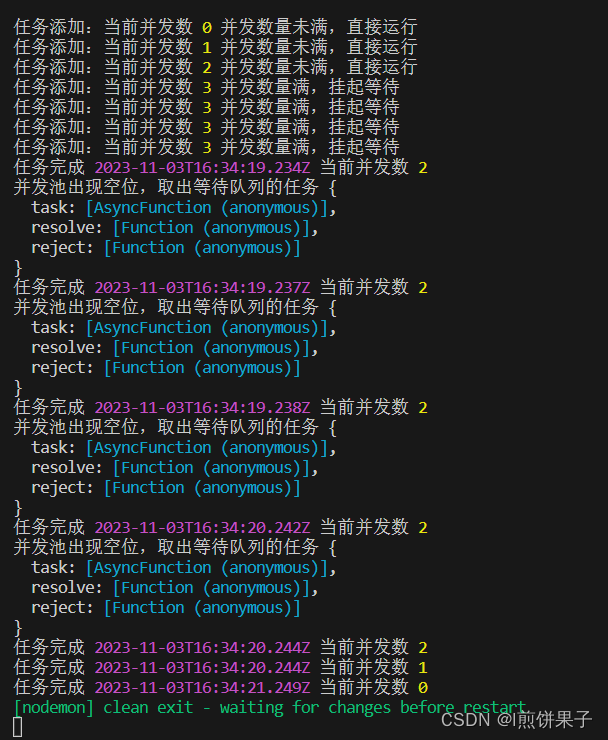
Promise的并发控制 - 从普通并发池到动态并发池
一、场景 给你一个有200个URL的数组,通过这些URL来发送请求,要求并发请求数不能超过五个。 这是一道很常考的面试题,接下来让我们来学习一下Promise并发控制 二、普通并发池的实现 主要思路就是,判断当前队列是否满,…...
Java类加载机制(类加载器,双亲委派模型,热部署示例)
Java类加载机制 类加载器类加载器的执行流程类加载器的种类加载器之间的关系ClassLoader 的主要方法Class.forName()与ClassLoader.loadClass()区别 双亲委派模型双亲委派 类加载流程优缺点 热部署简单示例 类加载器 类加载器的执行流程 类加载器的种类 AppClassLoader 应用类…...
【C语言初学者周冲刺计划】3.2将一个数组中的值逆序重新存放
目录 1解题思路: 2代码 3运行代码如图: 4总结: 1解题思路: 首先学会如何利用循环输入位数和输入数值,然后再利用循环逆序即可 2代码 #define _CRT_SECURE_NO_WARNINGS #include<stdio.h> int main() { int…...
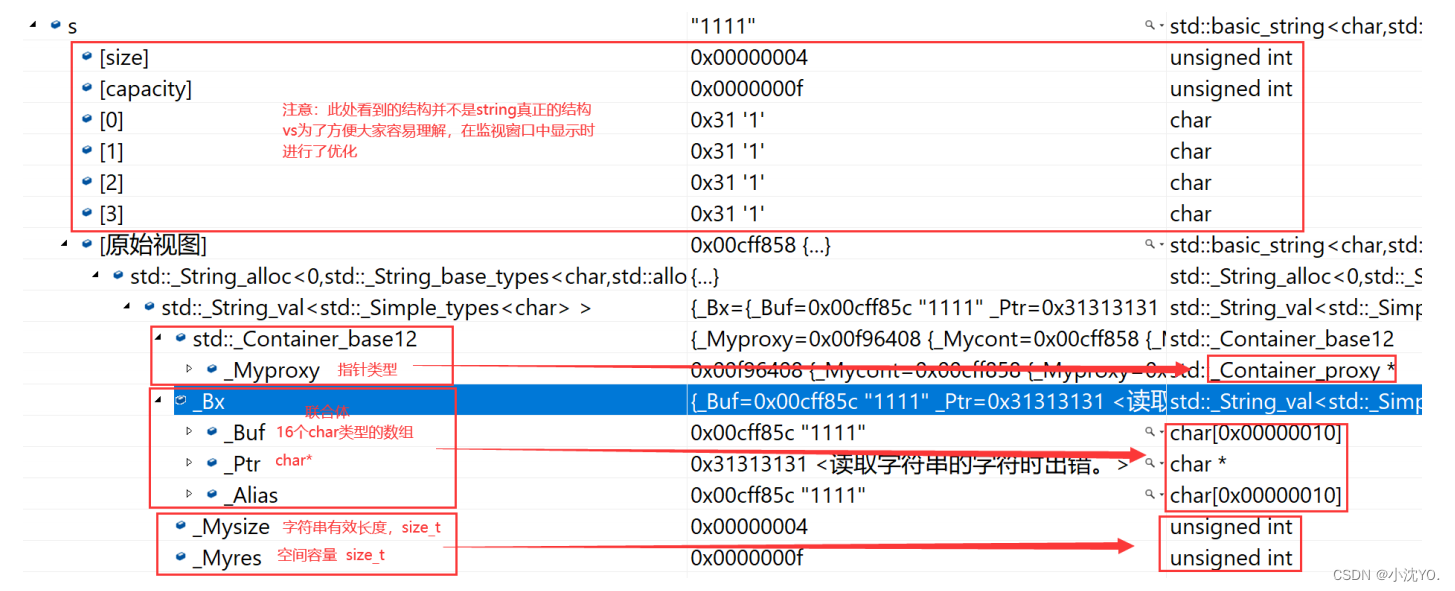
【C++心愿便利店】No.11---C++之string语法指南
文章目录 前言一、 为什么学习string类二、标准库中的string类 前言 👧个人主页:小沈YO. 😚小编介绍:欢迎来到我的乱七八糟小星球🌝 📋专栏:C 心愿便利店 🔑本章内容:str…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
