【考研数学】数学“背诵手册”(二)| 线代及概率论部分
文章目录
- 引言
- 二、线代
- 施密特正交化
- 分块矩阵
- 转置、逆、伴随之间的运算
- 关于秩
- 定义
- 性质
- 三、概统
- 常见分布的期望及方差
引言
这数一全部内容太多了,放在一篇文章里的话,要编辑就很困难,就把线代和概率放在这篇文章里吧。
二、线代
施密特正交化
把一组线性无关的向量组转化为一组两两正交且规范的向量组的过程,称为施密特正交化。
设 α 1 , α 2 , ⋯ , α n \pmb{\alpha_1,\alpha_2,\cdots,\alpha_n} α1,α2,⋯,αn 线性无关,其正交化过程为:
(1)正交化 l e t β 1 = α 1 , β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 β n = α n − ( α n , β 1 ) ( β 1 , β 1 ) β 1 − ( α n , β 2 ) ( β 2 , β 2 ) β 2 − ⋯ − ( α n , β n − 1 ) ( β n − 1 , β n − 1 ) β n − 1 let\space \pmb{\beta_1=\alpha_1,\beta_2=\alpha_2-\frac{(\alpha_2,\beta_1)}{(\beta_1,\beta_1)}\beta_1}\\ \pmb{\beta_n=\alpha_n-\frac{(\alpha_n,\beta_1)}{(\beta_1,\beta_1)}\beta_1-\frac{(\alpha_n,\beta_2)}{(\beta_2,\beta_2)}\beta_2}-\cdots-\pmb{\frac{(\alpha_n,\beta_{n-1})}{(\beta_{n-1},\beta_{n-1})}\beta_{n-1}} let β1=α1,β2=α2−(β1,β1)(α2,β1)β1βn=αn−(β1,β1)(αn,β1)β1−(β2,β2)(αn,β2)β2−⋯−(βn−1,βn−1)(αn,βn−1)βn−1 则向量组 β 1 , β 2 , ⋯ , β n \pmb{\beta_1,\beta_2,\cdots,\beta_n} β1,β2,⋯,βn 两两正交。
(2)规范化。各自除以各自的模即可。
分块矩阵
首先是行列式,有以下三个结论:
(1) ∣ A 1 A 2 ⋱ A n ∣ = ∣ A 1 ∣ ⋅ ∣ A 2 ∣ ⋯ ∣ A n ∣ . \begin{vmatrix} \pmb{A_1} & & & \\ & \pmb{A_2} & & \\ & & \ddots & \\ & & & \pmb{A_n}\end{vmatrix}=|\pmb{A_1}|\cdot|\pmb{A_2}|\cdots|\pmb{A_n}|. A1A2⋱An =∣A1∣⋅∣A2∣⋯∣An∣.
(2) ∣ A C O B ∣ = ∣ A O O B ∣ = ∣ A ∣ ⋅ ∣ B ∣ . \begin{vmatrix} \pmb{A} & \pmb{C}\\ \pmb{O}& \pmb{B} \end{vmatrix}=\begin{vmatrix} \pmb{A} & \pmb{O}\\ \pmb{O}& \pmb{B} \end{vmatrix}=|\pmb{A}|\cdot|\pmb{B}|. AOCB = AOOB =∣A∣⋅∣B∣.
(3)设 A , B \pmb{A,B} A,B 分别为 m , n m,n m,n 阶方阵,则有 ∣ O A B O ∣ = ( − 1 ) m n ∣ A ∣ ⋅ ∣ B ∣ . \begin{vmatrix} \pmb{O} & \pmb{A}\\ \pmb{B}& \pmb{O} \end{vmatrix}=(-1)^{mn}|\pmb{A}|\cdot|\pmb{B}|. OBAO =(−1)mn∣A∣⋅∣B∣.
然后是转置的结论: [ A B C D ] T = [ A T C T B T D T ] . \begin{bmatrix} \pmb{A} & \pmb{B}\\ \pmb{C}& \pmb{D} \end{bmatrix}^T=\begin{bmatrix} \pmb{A^T} & \pmb{C^T}\\ \pmb{B^T}& \pmb{D^T} \end{bmatrix}. [ACBD]T=[ATBTCTDT].
接着是逆矩阵的结论: [ A O O B ] − 1 = [ A − 1 O O B − 1 ] , [ O A B O ] − 1 = [ O B − 1 A − 1 O ] . \begin{bmatrix} \pmb{A} & \pmb{O}\\ \pmb{O}& \pmb{B} \end{bmatrix}^{-1}=\begin{bmatrix} \pmb{A^{-1}} & \pmb{O}\\ \pmb{O}& \pmb{B^{-1}} \end{bmatrix},\begin{bmatrix} \pmb{O} & \pmb{A}\\ \pmb{B}& \pmb{O} \end{bmatrix}^{-1}=\begin{bmatrix} \pmb{O} & \pmb{B^{-1}}\\ \pmb{A^{-1}}& \pmb{O} \end{bmatrix}. [AOOB]−1=[A−1OOB−1],[OBAO]−1=[OA−1B−1O].
转置、逆、伴随之间的运算
对可逆矩阵,转置、逆和伴随可以随意交换顺序,即 ( A − 1 ) T = ( A T ) − 1 , ( A ∗ ) − 1 = ( A − 1 ) ∗ , ( A ∗ ) T = ( A T ) ∗ . (\pmb{A}^{-1})^T=(\pmb{A}^{T})^{-1},(\pmb{A}^{*})^{-1}=(\pmb{A}^{-1})^{*},(\pmb{A}^{*})^T=(\pmb{A}^{T})^*. (A−1)T=(AT)−1,(A∗)−1=(A−1)∗,(A∗)T=(AT)∗.
关于秩
定义
矩阵的秩的定义:
设 A \pmb{A} A 是 m × n m\times n m×n 矩阵,从中任取 r r r 行 r r r 列,元素按照原有次序构成的 r r r 阶行列式,称为矩阵 A \pmb{A} A 的 r r r 阶子式。若 矩阵 A \pmb{A} A 中至少有一个 r r r 阶子式不为零,但所有 r + 1 r+1 r+1 阶子式(可能没有)均为零,称 r r r 为矩阵 A \pmb{A} A 的秩。
向量组秩的定义:
设 α 1 , α 2 , ⋯ , α n \pmb{\alpha_1,\alpha_2,\cdots,\alpha_n} α1,α2,⋯,αn 为一组向量,若其存在 r r r 个向量线性无关,且任意 r + 1 r+1 r+1 个向量(不一定有)一定线性相关,称这 r r r 个线性无关的向量构成的向量组为 α 1 , α 2 , ⋯ , α n \pmb{\alpha_1,\alpha_2,\cdots,\alpha_n} α1,α2,⋯,αn 的极大线性无关组,极大线性无关组所含向量的个数,称为向量组的秩。
性质
矩阵的秩有如下性质: r ( A ) = r ( A T ) = r ( A A T ) = r ( A T A ) . [ r ( A ) + r ( B ) − n ] ≤ r ( A + B ) ≤ r ( A ) + r ( B ) . r ( A B ) ≤ min { r ( A ) , r ( B ) } . i f A B = O , t h e n , r ( A ) + r ( B ) ≤ n . i f ∣ P ∣ , ∣ Q ∣ ≠ 0 , r ( A ) = r ( P A ) = r ( A Q ) = r ( P A Q ) . r ( A ∗ ) = { n r ( A ) = n 1 r ( A ) = n − 1 0 r ( A ) < n − 1 , ( n ≥ 2 ) . l e t A m × n , B m × s , t h e n , max { r ( A ) , r ( A ) } ≤ r ( A ⋮ B ) ≤ r ( A ) + r ( B ) . α , β ≠ 0 , r ( A ) = 1 ⟺ A = α β T . r ( A O O B ) = r ( A ) + r ( A ) . r(\pmb{A})=r(\pmb{A}^T)=r(\pmb{A}\pmb{A}^T)=r(\pmb{A}^T\pmb{A}).\\ [r(\pmb{A})+r(\pmb{B})-n]\leq r(\pmb{A}+\pmb{B})\leq r(\pmb{A})+r(\pmb{B}). \\ r(\pmb{AB})\leq \min\{r(\pmb{A}),r(\pmb{B})\}. \\ if\space \pmb{AB=O},then\space ,r(\pmb{A})+r(\pmb{B})\leq n. \\ if\space |\pmb{P}|,|\pmb{Q}|\ne0,r(\pmb{A})=r(\pmb{PA})=r(\pmb{AQ})=r(\pmb{PAQ}).\\ r(\pmb{A}^*)=\begin{cases} n&r(\pmb{A})=n\\ 1&r(\pmb{A})=n-1\\ 0&r(\pmb{A})<n-1 \end{cases},(n\geq2).\\ let\space \pmb{A}_{m\times n},\pmb{B}_{m\times s},then,\max\{r(\pmb{A}),r(\pmb{A})\}\leq r(\pmb{A}\space\vdots \space B)\leq r(\pmb{A})+r(\pmb{B}). \\ \pmb{\alpha,\beta\ne 0},r(\pmb{A})=1 \pmb{\Longleftrightarrow} \pmb{A}=\pmb{\alpha\beta}^T.\\ r\begin{pmatrix} \pmb{A} & \pmb{O} \\ \pmb{O}& \pmb{B}\end{pmatrix}=r(\pmb{A})+r(\pmb{A}). r(A)=r(AT)=r(AAT)=r(ATA).[r(A)+r(B)−n]≤r(A+B)≤r(A)+r(B).r(AB)≤min{r(A),r(B)}.if AB=O,then ,r(A)+r(B)≤n.if ∣P∣,∣Q∣=0,r(A)=r(PA)=r(AQ)=r(PAQ).r(A∗)=⎩ ⎨ ⎧n10r(A)=nr(A)=n−1r(A)<n−1,(n≥2).let Am×n,Bm×s,then,max{r(A),r(A)}≤r(A ⋮ B)≤r(A)+r(B).α,β=0,r(A)=1⟺A=αβT.r(AOOB)=r(A)+r(A).
三、概统
常见分布的期望及方差
{ 分布 ‾ 分布律或概率密度 ‾ 数学期望 ‾ 方差 ‾ ( 0 − 1 )分布 P { X = k } = p k ( 1 − p ) 1 − k , k = 0 , 1 p p ( 1 − p ) 二项分布 P { X = k } = C n k p k ( 1 − p ) n − k , k = 0 ⋯ n n p n p ( 1 − p ) 泊松分布 P { X = k } = λ k k ! e − λ , k = 0 , 1 , 2 , ⋯ λ λ 正态分布 f ( x ) = 1 2 π σ E X P ( − ( x − μ ) 2 2 σ 2 ) μ σ 2 几何分布 P { X = k } = ( 1 − p ) k − 1 p , k = 1 , 2 , ⋯ 1 / p ( 1 − p ) / p 2 \begin{cases}\underline{分布}&\underline{分布律或概率密度}&\underline{数学期望}&\underline{方差}\\ (0-1)分布&P\{X=k\}=p^k(1-p)^{1-k},k=0,1&p&p(1-p)\\ 二项分布& P\{X=k\}=C_n^kp^k(1-p)^{n-k},k=0\cdots n&np&np(1-p)\\ 泊松分布&P\{X=k\}=\frac{\lambda^k}{k!}e^{-\lambda},k=0,1,2,\cdots&\lambda&\lambda \\ 正态分布 & f(x)=\frac{1}{\sqrt{2\pi}\sigma}E XP(-\frac{(x-\mu)^2}{2\sigma^2})&\mu&\sigma^2\\ 几何分布&P\{X=k\}=(1-p)^{k-1}p,k=1,2,\cdots&1/p&(1-p)/p^2\end{cases} ⎩ ⎨ ⎧分布(0−1)分布二项分布泊松分布正态分布几何分布分布律或概率密度P{X=k}=pk(1−p)1−k,k=0,1P{X=k}=Cnkpk(1−p)n−k,k=0⋯nP{X=k}=k!λke−λ,k=0,1,2,⋯f(x)=2πσ1EXP(−2σ2(x−μ)2)P{X=k}=(1−p)k−1p,k=1,2,⋯数学期望pnpλμ1/p方差p(1−p)np(1−p)λσ2(1−p)/p2 均匀分布: f ( x ) = { 1 / ( b − a ) , a < x < b 0 , e l s e , E ( X ) = a + b 2 , D ( X ) = ( b − a ) 2 12 . f(x)=\begin{cases} 1/(b-a),&a<x<b \\ 0,&else \end{cases},E(X)=\frac{a+b}{2},D(X)=\frac{(b-a)^2}{12}. f(x)={1/(b−a),0,a<x<belse,E(X)=2a+b,D(X)=12(b−a)2. 指数分布: f ( x ) = { λ e − λ x , x > 0 0 , e l s e , E ( X ) = 1 λ , D ( X ) = 1 λ 2 . f(x)=\begin{cases} \lambda e^{-\lambda x},&x>0 \\ 0,&else \end{cases},E(X)=\frac{1}{\lambda},D(X)=\frac{1}{\lambda^2}. f(x)={λe−λx,0,x>0else,E(X)=λ1,D(X)=λ21.
相关文章:
| 线代及概率论部分)
【考研数学】数学“背诵手册”(二)| 线代及概率论部分
文章目录 引言二、线代施密特正交化分块矩阵转置、逆、伴随之间的运算关于秩定义性质 三、概统常见分布的期望及方差 引言 这数一全部内容太多了,放在一篇文章里的话,要编辑就很困难,就把线代和概率放在这篇文章里吧。 二、线代 施密特正交…...
)
Android WMS——WindowState介绍(十三)
前面文章中的 addWindow 方法,首先获取了 DisplayContent,紧接着判断窗口的 type 类型并标记。然后获取 token 信息,且该信息是通过 DisplayContent 中的方法获取的。最后就是创建并保存 WindowState 信息。 一、简介 在窗口管理系统(Window Manager Service,WMS)中,Wi…...
C/C++网络编程基础知识超详细讲解第二部分(系统性学习day12)
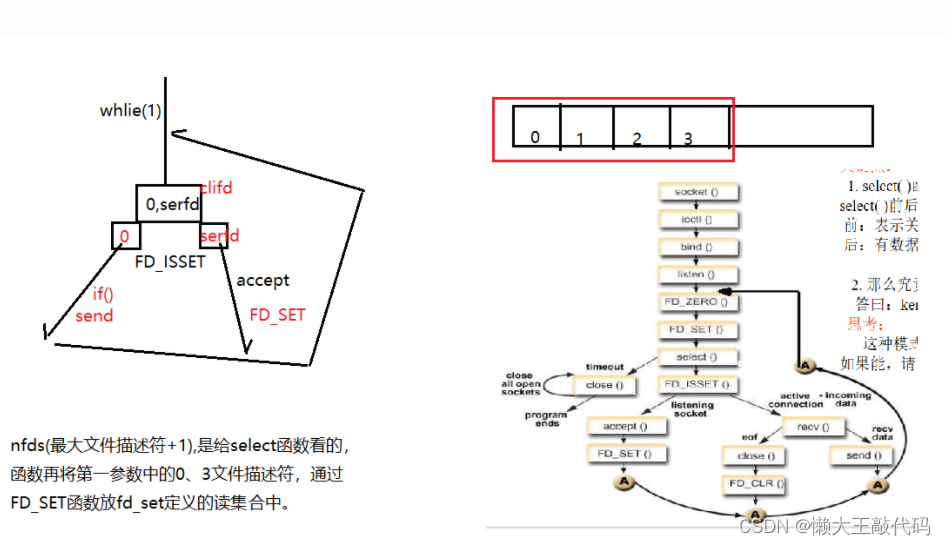
懒大王感谢大家的关注和三连支持~ 目录 前言 一、UDP编程 UDP特点: UDP框架: UDP函数学习 发送端代码案例如下: 二、多路复用 前提讲述 select poll 三、图解如下 总结 前言 作者简介: 懒大王敲代码,…...

【教3妹学编程-算法题】117. 填充每个节点的下一个右侧节点指针 II
2哥 : 3妹,听说你昨天去面试了,怎么样啊? 3妹:嗨,别提了,让我回去等通知,估计是没有通知了, 还浪费我请了一天假。 2哥 : 你又请假了啊, 你是怎么跟你那个严厉的老板请假…...
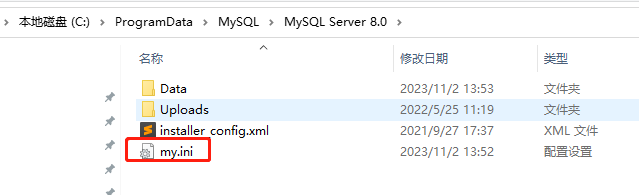
window10 mysql8.0 修改端口port不生效
mysql的默认端口是3306,我想修改成3307。 查了一下资料,基本上都是说先进入C:\Program Files\MySQL\MySQL Server 8.0这个目录。 看看有没有my.ini,没有就新建。 我这里没有,就新建一个,然后修改port: […...
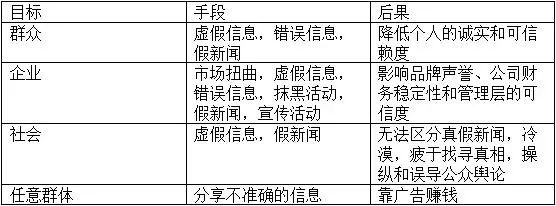
欧盟网络安全威胁:虚假与错误信息
如今,数字平台已是新闻媒体的主战地。社交网站、新闻媒体、甚至搜索引擎都是现在大多数人的信息来源。由于这些网站的运作方式是通过吸引人们来产生网站流量,这些抓人眼球的信息通常是推广广告,有些甚至没有经过审查。 国际现状 恶意攻击者现…...
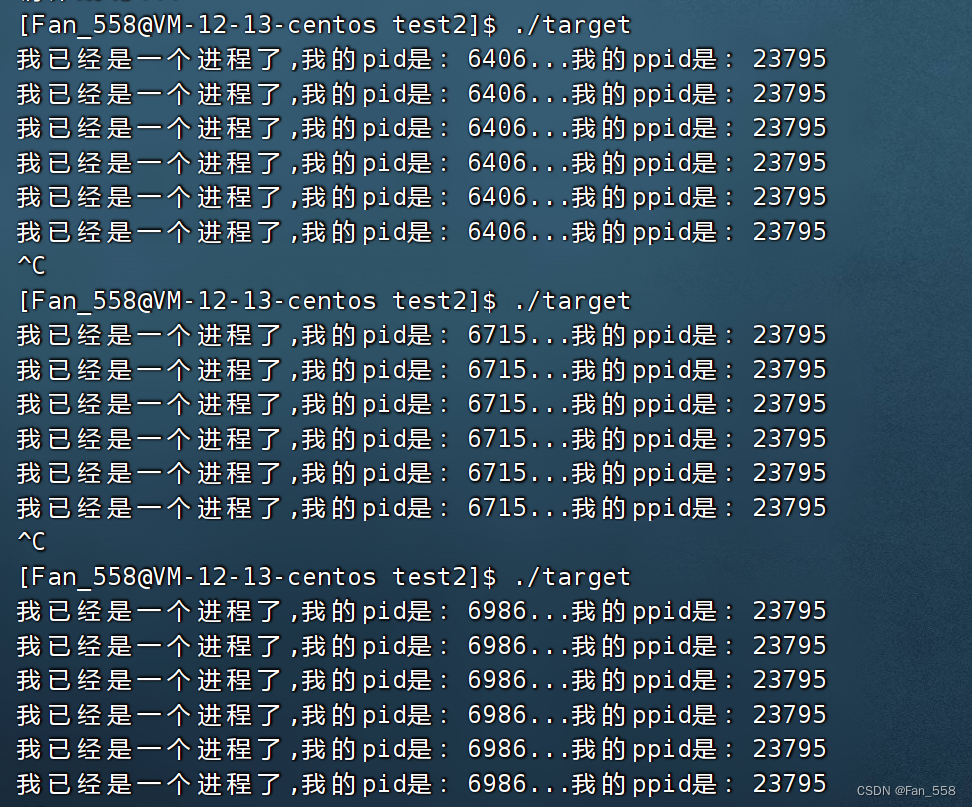
006 Linux 进程的概念 | 获取进程的PID
前言 本文将会向您进程的概念,程序与进程的区别,如何获取进程的标识符-pid 文章重点 1.描述进程——PCB 进程与程序的区别 CPU对进程列表的处理 2.获取进程PID 描述进程-PCB 进程概念 课本概念:程序的一个执行实例或正在执行的程序 内核…...
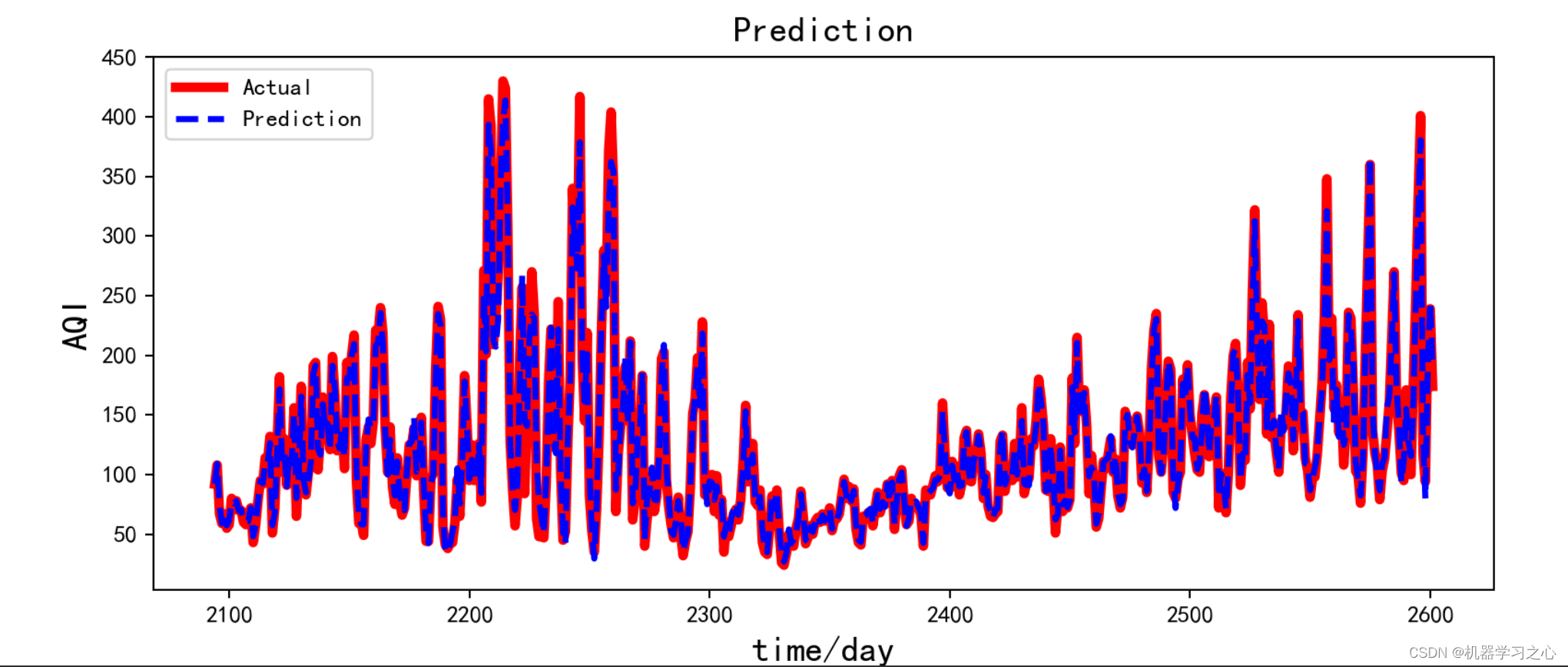
时序预测 | Python实现ARIMA-CNN-LSTM差分自回归移动平均模型结合卷积长短期记忆神经网络时间序列预测
时序预测 | Python实现ARIMA-CNN-LSTM差分自回归移动平均模型结合卷积长短期记忆神经网络时间序列预测 目录 时序预测 | Python实现ARIMA-CNN-LSTM差分自回归移动平均模型结合卷积长短期记忆神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 时序预测 …...

《异常检测——从经典算法到深度学习》23 TimesNet: 用于常规时间序列分析的时间二维变化模型
zz# 《异常检测——从经典算法到深度学习》 0 概论1 基于隔离森林的异常检测算法 2 基于LOF的异常检测算法3 基于One-Class SVM的异常检测算法4 基于高斯概率密度异常检测算法5 Opprentice——异常检测经典算法最终篇6 基于重构概率的 VAE 异常检测7 基于条件VAE异常检测8 Don…...
)
计算机网络(59)
1. OSI 的七层模型分别是?各自的功能是什么? 2. 为什么需要三次握手?两次不行? 3. 为什么需要四次挥手?三次不行? 4. TCP与UDP有哪些区别?各自应用场景? 5. HTTP1.0,1.1&…...
【CSS】CSS基础知识扫盲
1、 什么是CSS? CSS即层叠样式表 (Cascading Style Sheets). CSS 能够对网页中元素位置的排版进行像素级精确控制, 实现美化页面的效果. 能够做到页面的样式和结构分离 2、 CSS引入方式 CSS代码编写的时候有多种引入方式: 内部样式、外部样式、内联样…...

React中的状态管理
目录 前言 1. React中的状态管理 1.1 本地状态管理 1.2 全局状态管理 Redux React Context 2. React状态管理的优势 总结 前言 当谈到前端开发中的状态管理时,React是一个备受推崇的选择。React的状态管理机制被广泛应用于构建大型、复杂的应用程序…...

【优选算法系列】【专题九链表】第一节.链表常用技巧和操作总结(2. 两数相加)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、链表常用技巧和操作总结二、两数相加 2.1 题目描述 2.2 题目解析 2.2.1 算法原理 2.2.2 代码编写总结 前言 一、链表常…...
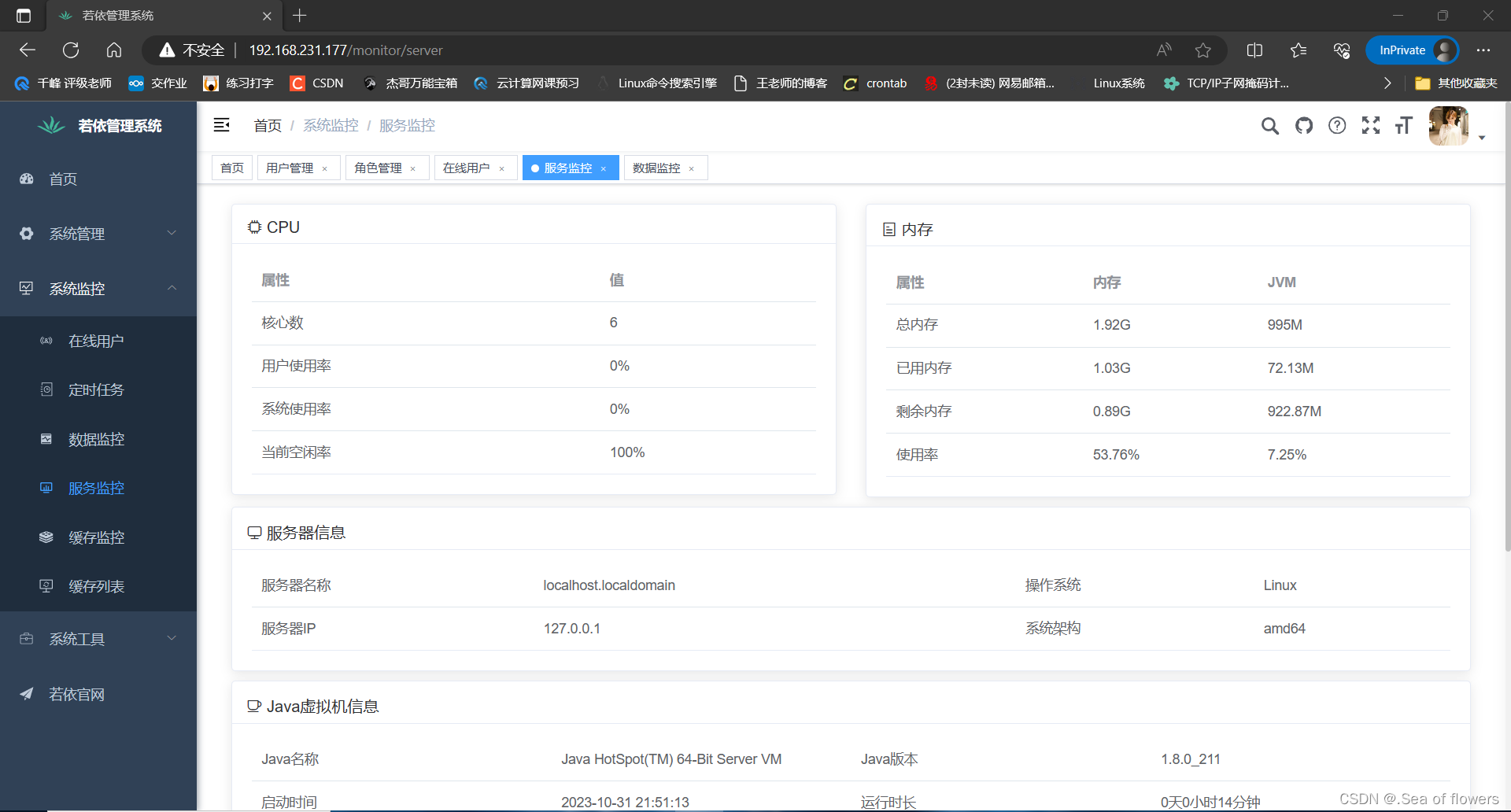
上线Spring boot-若依项目
基础环境 所有环境皆关闭防火墙与selinux 服务器功能主机IP主机名服务名称配置前端服务器192.168.231.177nginxnginx1C2G后端服务器代码打包192.168.231.178javajava、maven、nodejs4C8G数据库/缓存192.168.231.179dbmysql、redis2C4G Nginx #配置Nginxyum源 [rootnginx ~]…...
pinia简单使用
新命令-创建vue3项目 vue create 方式使用脚手架创建项目,vue cli处理, vue3后新的脚手架工具create-vue 使用npm init vuelatest 命令创建即可。 在pinia中,将使用的组合式函数识别为状态管理内容 自动将ref 识别为stste,computed 相当于 ge…...
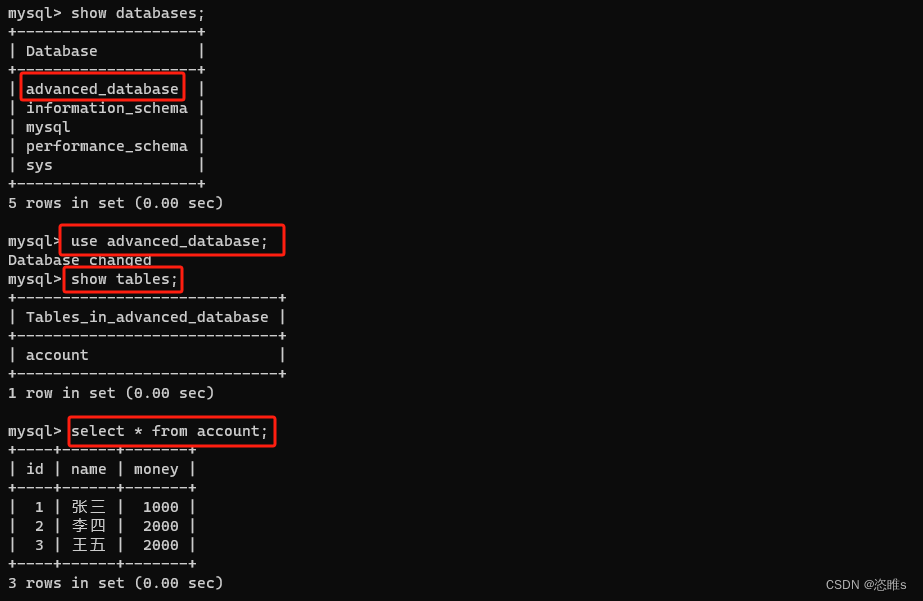
数据库进阶教学——数据库故障恢复(日志文件)
目录 一、日志简介 二、日志文件操作 1、查看日志状态 2、开启日志功能 3、查看日志文件 4、查看当前日志 5、查看日志中的事件 6、删除日志文件 7、查看和修改日志文件有效期 8、查看日志文件详细信息 三、删除的数据库恢复 一、日志简介 日志是记录所有数据库表结…...
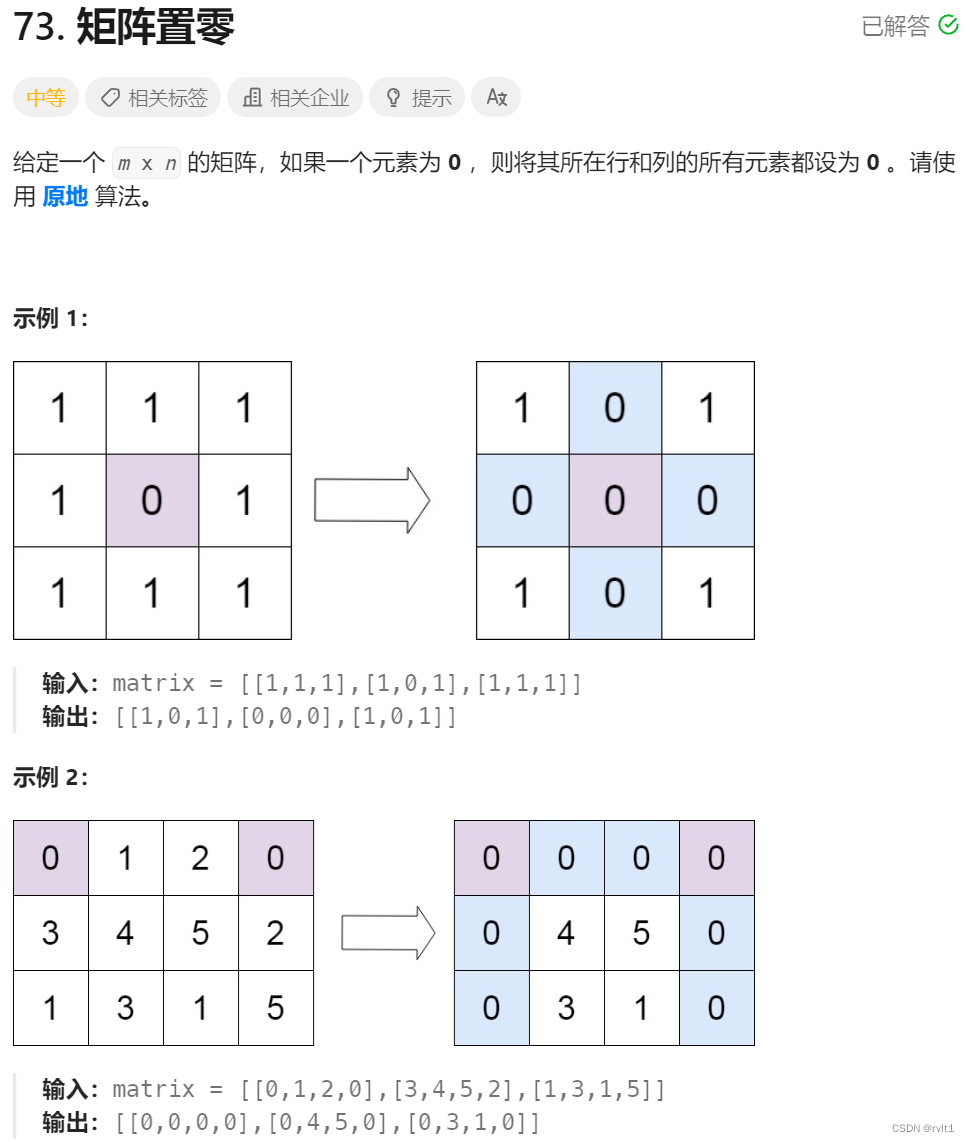
Leetcode 73 矩阵置0
class Solution {//1.用矩阵的第一行和第一列来标记该行或该列是否应该为0,但是这样的话忽视了第一行或第一列为0的情况//2.用标记row0和column0来标记第一行或第一列是否该为0public void setZeroes(int[][] matrix) {int n matrix.length;int m matrix[0].length;boolean r…...

Rust学习日记(二)变量的使用--结合--温度换算/斐波那契数列--实例
前言: 这是一个系列的学习笔记,会将笔者学习Rust语言的心得记录。 当然,这并非是流水账似的记录,而是结合实际程序项目的记录,如果你也对Rust感兴趣,那么我们可以一起交流探讨,使用Rust来构建程…...

html各个标签的使用
一、标签的分类 1、单标签和双标签 1. 单标签:<img> img br hr 2. 双标签:<div></div> div span <a></a> h p a 2、按照标签属性分类 1. 块标签:自己独占一行 h1~h6 p div 2. 行内(内联)标签 …...

android 混淆
# 指定代码的压缩级别 0 - 7(指定代码进行迭代优化的次数,在Android里面默认是5,这条指令也只有在可以优化时起作用。) -optimizationpasses 5 # 混淆时不会产生形形色色的类名(混淆时不使用大小写混合类名) -dontusemixedcaseclassnames # 指定不去忽略…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

Docker、Wsl 打包迁移环境
电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本: 2.2.4.0 内核版本: 5.15.153.1-2 WSLg 版本: 1.0.61 MSRDC 版本: 1.2.5326 Direct3D 版本: 1.611.1-81528511 DXCore 版本: 10.0.2609…...

STM32CubeMX-H7-19-ESP8266通信(中)--单片机控制ESP8266实现TCP地址通信
前言 上篇文章我们已经能够使用串口助手实现esp8266的几种通信,接下来我们使用单片机控制实现。这篇文章会附带教程,增加.c和,.h,把串口和定时器放到对应的编号,然后调用初始化就可以使用了。 先讲解,然后末尾再放源码…...

MySQL技术内幕1:内容介绍+MySQL编译使用介绍
文章目录 1.整体内容介绍2.下载编译流程2.1 安装编译工具和依赖库2.2 下载编译 3.配置MySQL3.1 数据库初始化3.2 编辑配置文件3.3 启动停止MySQL3.4 登录并修改密码 1.整体内容介绍 MySQL技术系列文章将从MySQL下载编译,使用到MySQL各组件使用原理源码分析…...

奈飞工厂官网,国内Netflix影视在线看|中文网页电脑版入口
奈飞工厂是一个专注于提供免费Netflix影视资源的在线播放平台,致力于为国内用户提供的Netflix热门影视内容。该平台的资源与Netflix官网基本同步,涵盖电影、电视剧、动漫和综艺等多个领域。奈飞工厂的界面简洁流畅,资源分类清晰,方…...
