代码随想录算法训练营第四十二天丨 动态规划part05
1049.最后一块石头的重量II
思路
本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。
本题物品的重量为 stones[i],物品的价值也为 stones[i]。
对应着01背包里的物品重量 weight[i]和 物品价值 value[i]。
接下来进行动规五步曲:
- 确定dp数组以及下标的含义
dp[j]表示容量(这里说容量更形象,其实就是重量)为j的背包,最多可以背最大重量为dp[j]。
可以回忆一下01背包中,dp[j]的含义,容量为j的背包,最多可以装的价值为 dp[j]。
相对于 01背包,本题中,石头的重量是 stones[i],石头的价值也是 stones[i] ,可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]”
- 确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题则是:dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
一些同学可能看到这dp[j - stones[i]] + stones[i]中 又有- stones[i] 又有+stones[i],看着有点晕乎。
大家可以再去看 dp[j]的含义。
- dp数组如何初始化
既然 dp[j]中的j表示容量,那么最大容量(重量)是多少呢,就是所有石头的重量和。
因为提示中给出1 <= stones.length <= 30,1 <= stones[i] <= 1000,所以最大重量就是30 * 1000
而我们要求的target其实只是最大重量的一半,所以dp数组开到15000大小就可以了。
当然也可以把石头遍历一遍,计算出石头总重量 然后除2,得到dp数组的大小。
我这里就直接用15000了。
接下来就是如何初始化dp[j]呢,因为重量都不会是负数,所以dp[j]都初始化为0就可以了,这样在递归公式dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);中 dp[j]才不会初始值所覆盖。
代码为:
int[] dp = new int[target+1];- 确定遍历顺序
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中就已经说明:如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
代码如下:
for (int i = 0; i < stones.size(); i++) { // 遍历物品for (int j = target; j >= stones[i]; j--) { // 遍历背包dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);}
}- 举例推导dp数组
举例,输入:[2,4,1,1],此时target = (2 + 4 + 1 + 1)/2 = 4 ,dp数组状态图如下:
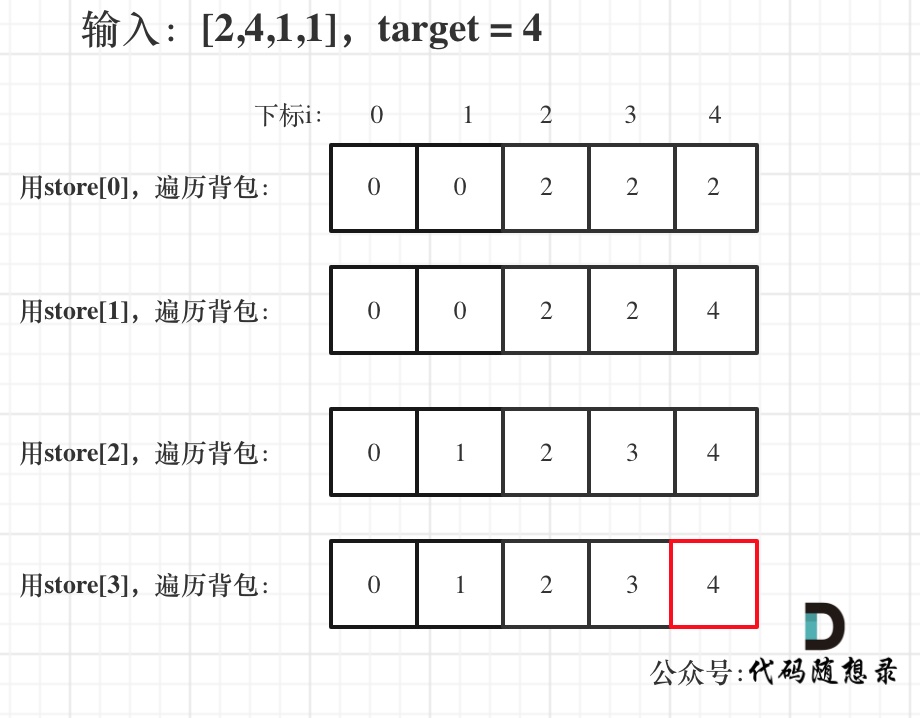
最后dp[target]里是容量为target的背包所能背的最大重量。
那么分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum - dp[target]。
在计算target的时候,target = sum / 2 因为是向下取整,所以sum - dp[target] 一定是大于等于dp[target]的。
那么相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]。
代码如下:
class Solution {public int lastStoneWeightII(int[] stones) {//确定dp数组及其下标含义//dp数组将石头堆分成两堆,使两堆的int sum = 0;for (int i = 0; i < stones.length; i++) {sum += stones[i];}int target = sum / 2;int[] dp = new int[target+1];for (int i = 0; i < stones.length; i++) {for (int j = target; j >= stones[i]; j--) {dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2*dp[target];}
}494.目标和
思路
这道题目咋眼一看和动态规划背包啥的也没啥关系。
本题要如何使表达式结果为target,
既然为target,那么就一定有 left组合 - right组合 = target。
left + right = sum,而sum是固定的。right = sum - left
公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
target是固定的,sum是固定的,left就可以求出来。
此时问题就是在集合nums中找出和为left的组合
动态规划
如何转化为01背包问题呢。
假设加法的总和为x,那么减法对应的总和就是sum - x。
所以我们要求的是 x - (sum - x) = target
x = (target + sum) / 2
此时问题就转化为,装满容量为x的背包,有几种方法。
这里的x,就是bagSize,也就是我们后面要求的背包容量。
大家看到(target + sum) / 2 应该担心计算的过程中向下取整有没有影响。
这么担心就对了,例如sum 是5,S是2的话其实就是无解的,所以:
(C++代码中,输入的S 就是题目描述的 target)
if ((S + sum) % 2 == 1) return 0; // 此时没有方案
同时如果 S的绝对值已经大于sum,那么也是没有方案的。
(C++代码中,输入的S 就是题目描述的 target)
if (abs(S) > sum) return 0; // 此时没有方案
再回归到01背包问题,为什么是01背包呢?
因为每个物品(题目中的1)只用一次!
这次和之前遇到的背包问题不一样了,之前都是求容量为j的背包,最多能装多少。
本题则是装满有几种方法。其实这就是一个组合问题了。
- 确定dp数组以及下标的含义
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法
其实也可以使用二维dp数组来求解本题,dp[i][j]:使用 下标为[0, i]的nums[i]能够凑满j(包括j)这么大容量的包,有dp[i][j]种方法。
下面都是统一使用一维数组进行讲解, 二维降为一维(滚动数组),其实就是上一层拷贝下来,这个我在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)也有介绍。
- 确定递推公式
有哪些来源可以推出dp[j]呢?
只要搞到nums[i],凑成dp[j]就有dp[j - nums[i]] 种方法。
例如:dp[j],j 为5,
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
- 已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 容量为5的背包
- 已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 容量为5的背包
- 已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 容量为5的背包
那么凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
所以求组合类问题的公式,都是类似这种:
dp[j] += dp[j - nums[i]]
这个公式在后面在讲解背包解决排列组合问题的时候还会用到!
- dp数组如何初始化
从递推公式可以看出,在初始化的时候dp[0] 一定要初始化为1,因为dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递推结果将都是0。
这里有录友可能认为从dp数组定义来说 dp[0] 应该是0,也有录友认为dp[0]应该是1。
其实不要硬去解释它的含义,咱就把 dp[0]的情况带入本题看看应该等于多少。
如果数组[0] ,target = 0,那么 bagSize = (target + sum) / 2 = 0。 dp[0]也应该是1, 也就是说给数组里的元素 0 前面无论放加法还是减法,都是 1 种方法。
所以本题我们应该初始化 dp[0] 为 1。
可能有同学想了,那 如果是 数组[0,0,0,0,0] target = 0 呢。
其实 此时最终的dp[0] = 32,也就是这五个零 子集的所有组合情况,但此dp[0]非彼dp[0],dp[0]能算出32,其基础是因为dp[0] = 1 累加起来的。
dp[j]其他下标对应的数值也应该初始化为0,从递推公式也可以看出,dp[j]要保证是0的初始值,才能正确的由dp[j - nums[i]]推导出来。
- 确定遍历顺序
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中,我们讲过对于01背包问题一维dp的遍历,nums放在外循环,target在内循环,且内循环倒序。
- 举例推导dp数组
输入:nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:

代码如下:
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int i = 0; i < nums.length; i++) sum += nums[i];//如果target过大 sum将无法满足if ( target < 0 && sum < -target) return 0;if ((target + sum) % 2 != 0) return 0;int size = (target + sum) / 2;if(size < 0) size = -size;int[] dp = new int[size + 1];dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = size; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[size];}
}474.一和零
思路
这道题目,还是比较难的,也有点像程序员自己给自己出个脑筋急转弯,程序员何苦为难程序员呢。
本题并不是多重背包,再来看一下这个图,捋清几种背包的关系
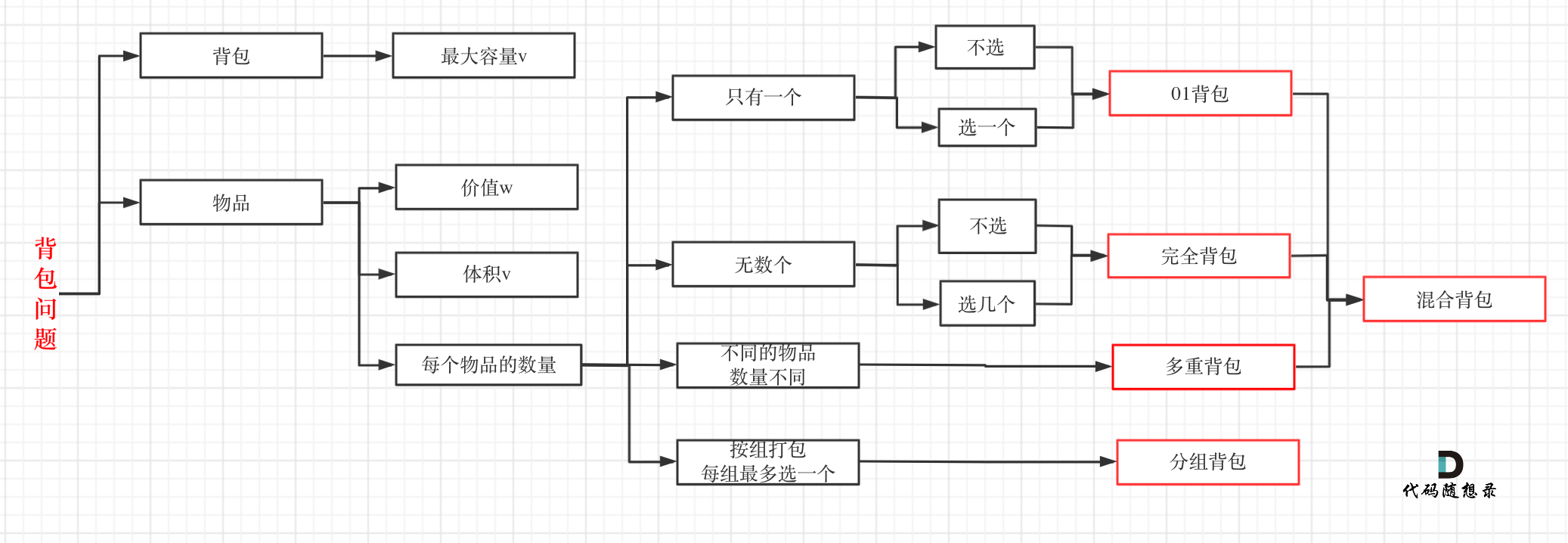
多重背包是每个物品,数量不同的情况。
本题中strs 数组里的元素就是物品,每个物品都是一个!
而m 和 n相当于是一个背包,两个维度的背包。
理解成多重背包的主要是把m和n混淆为物品了,感觉这是不同数量的物品,所以以为是多重背包。
但本题其实是01背包问题!
只不过这个背包有两个维度,一个是m 一个是n,而不同长度的字符串就是不同大小的待装物品。
开始动规五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
- 确定递推公式
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
此时大家可以回想一下01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
对比一下就会发现,字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
这就是一个典型的01背包! 只不过物品的重量有了两个维度而已。
- dp数组如何初始化
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中已经讲解了,01背包的dp数组初始化为0就可以。
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
- 确定遍历顺序
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中,我们讲到了01背包为什么一定是外层for循环遍历物品,内层for循环遍历背包容量且从后向前遍历!
那么本题也是,物品就是strs里的字符串,背包容量就是题目描述中的m和n。
代码如下:
for (String str : strs) {// 遍历物品//0 的个数int x = 0;//1 的个数int y = 0;for (char c : str.toCharArray()) {if (c=='0'){x++;}else if (c=='1'){y++;}}for (int i = m; i >= x; i--) {// 遍历背包容量且从后向前遍历!for (int j = n; j >= y; j--) {dp[i][j] = Math.max(dp[i][j],dp[i-x][j-y]+1);}}
}那个遍历背包容量的两层for循环先后循序有没有什么讲究?
没讲究,都是物品重量的一个维度,先遍历哪个都行!
- 举例推导dp数组
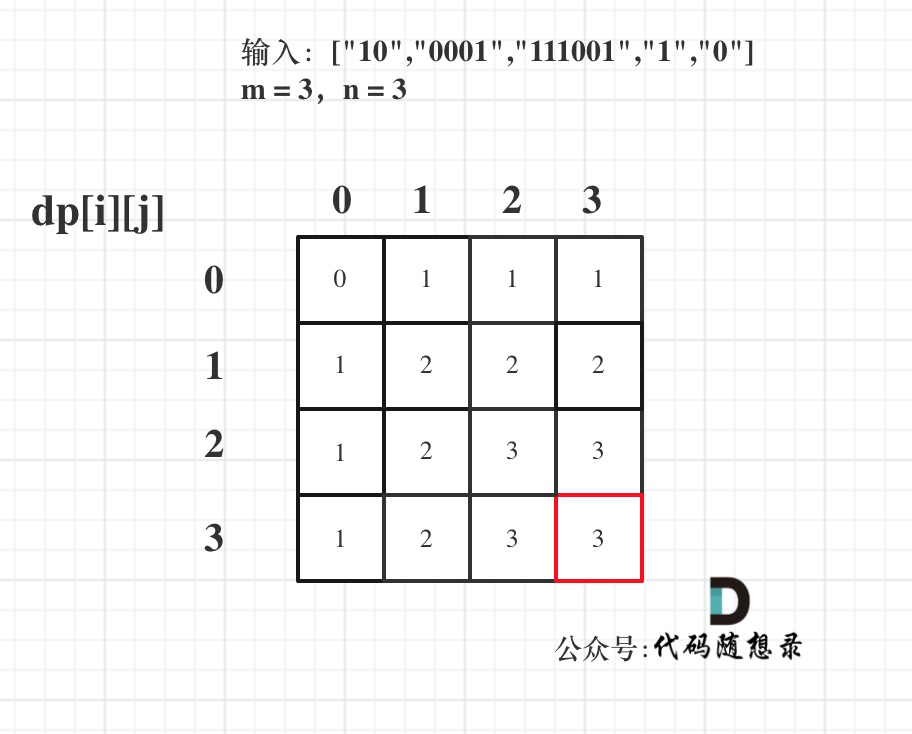
以输入:["10","0001","111001","1","0"],m = 3,n = 3为例
最后dp数组的状态如下所示:
代码如下:
class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m+1][n+1];for (String str : strs) {// 遍历物品//0 的个数int x = 0;//1 的个数int y = 0;for (char c : str.toCharArray()) {if (c=='0'){x++;}else if (c=='1'){y++;}}for (int i = m; i >= x; i--) {// 遍历背包容量且从后向前遍历!for (int j = n; j >= y; j--) {dp[i][j] = Math.max(dp[i][j],dp[i-x][j-y]+1);}}}return dp[m][n];}
}动态规划真想不出来,感觉是强行将题目解释成01背包问题的
相关文章:

代码随想录算法训练营第四十二天丨 动态规划part05
1049.最后一块石头的重量II 思路 本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。 感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。 本题物品的重量为 stones[i],物品的价…...

[css] flex 子元素自动撑开父元素宽度
对于水平排列的情况,我们可以设置父元素的flex-direction属性为row。这样,子元素将会水平排列在一行内,并自动撑开父元素的宽度。如果子元素的宽度总和超过了父元素的宽度,则子元素会被压缩,以适应父元素的宽度。 对于…...
全新干货!一招教你迅速提升流量主收入!包你轻松月入过万
也不怕大家笑话,才哥以前收入每天才一块钱,连瓶水都买不了, 可是自从我开始接触老年粉私域后,一个搬运公众号的流量主收益两个月后就可以用“浴火重生”来形容了。 一个搬运公众号一天的流量主收益比我原创两年的个人公众号收益还…...

连接两个dataframe
concat import pandas as pd df1 pd.DataFrame({‘A’: [1, 2, 3], ‘B’: [4, 5, 6]}) df2 pd.DataFrame({‘A’: [7, 8, 9], ‘B’: [10, 11, 12]}) result pd.concat([df1, df2]) # 在行上连接 merge import pandas as pd df1 pd.DataFrame({‘key’: [‘A’, ‘B…...
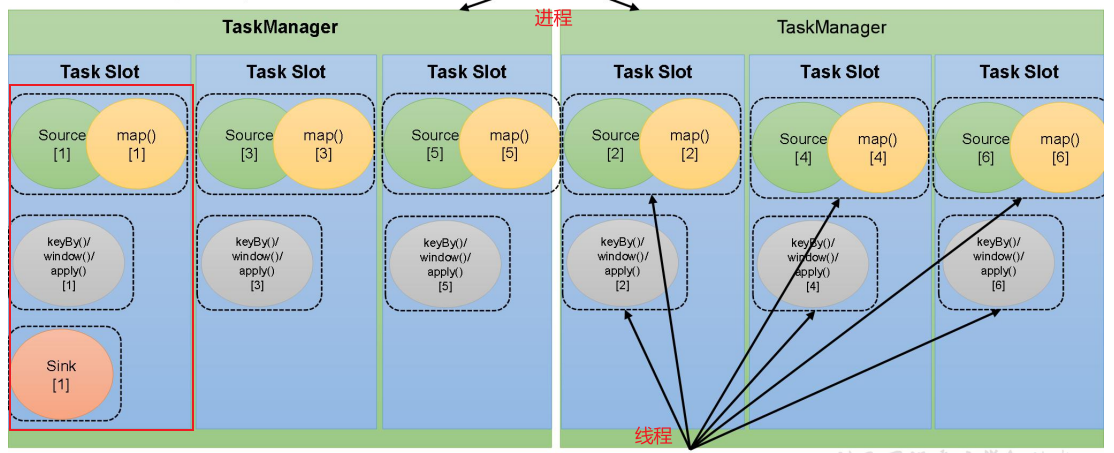
【入门Flink】- 05Flink运行时架构以及一些核心概念
系统架构 Flink运行时架构Standalone会话模式为例 1)作业管理器(JobManager) JobManager 是一个 Flink 集群中任务管理和调度的核心,是控制应用执行的主进程。每个应用都应该被唯一的 JobManager 所控制执行。 JobManger 又包含…...
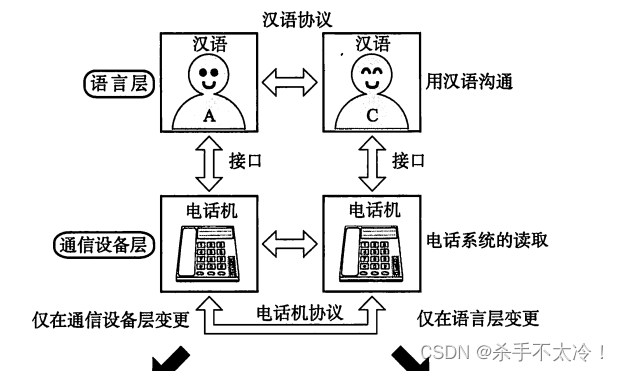
网络协议的基本概念
网络协议的基本概念 随处可见的协议 在计算机网络与信息通信领域里,人们经常提及“协议”一词。互联网中常用的具有代表性的协议有IP、TCP、HTTP等。 “计算机网络体系结构”将这些网络协议进行了系统归纳。TCP/IP就是IP、TCP、HTTP等协议的集合。现在࿰…...

广汽传祺E9上市,3DCAT实时云渲染助力线上3D高清看车体验
今年5月21日,中国智电新能源旗舰MPV——广汽传祺智电新能源E9在北京人民大会堂举办上市发布会。 发布会现场(图源官方) 为了让更多的消费者能够在线上感受到广汽传祺E9的魅力,3DCAT实时渲染云与大圣科技合作为广汽传祺打造了一款…...
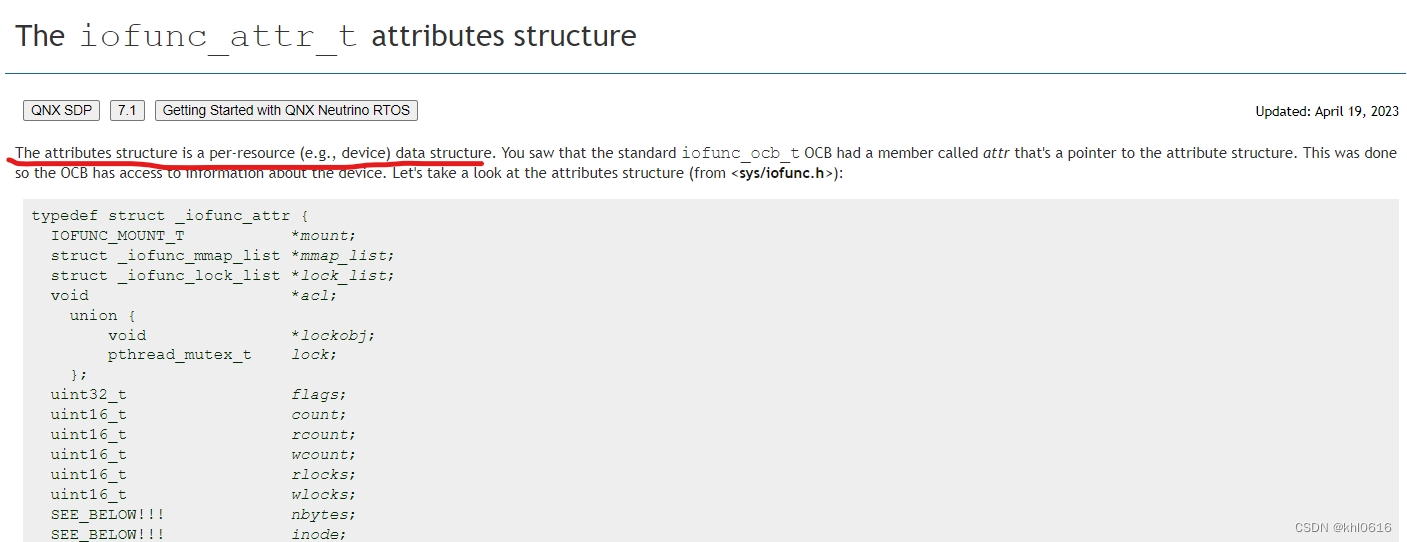
resource manager attributes structure(iofunc_attr_t) 扩展实例
文章目录 前言一、attributes structure(iofunc_attr_t)是什么二、iofunc_attr_t 扩展实例1. iofunc_attr_t 未扩展前的使用实例2. iofunc_attr_t 扩展后的使用实例总结参考资料前言 本文主要介绍如何扩展 QNX resource manager 的 attributes structure(iofunc_attr_t) 属性数…...
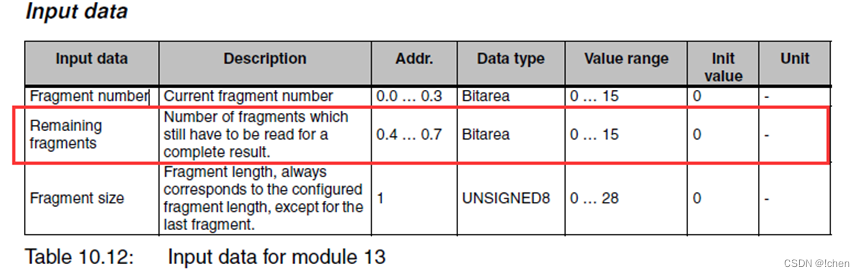
劳易测扫码条码分段读取实现方法
添加如下3个功能块:M10,M13和M27 设置BCL参数:Code type 1 为Code128 参数:Mode为Range 参数:Number Of digits 1 为条码最小长度 Number Of digits 2 为条码最大长度。 设置M10:Mode(With …...

【Linux】Nignx及负载均衡动静分离
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《微信小程序开发实战》。🎯Ἲ…...

AI:50-基于深度学习的柑橘类水果分类
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌本专栏包含以下学习方向: 机器学习、深度学…...

mysql 中!= 到底走不走索引?
mysql 中! 到底走不走索引? 很多人疑惑! 到底走不走索引, 这里可以肯定的说该操作是可以走索引的,但实际情况中都为啥都不走索引呢? 首先我们要知道走索引与数据量和数据趋势(cardinality)有很大的关系&…...

4 sql语法基础
1、DISTINCT 相同值只会出现一次。它作用于所有列,也就是说所有列的值都相同才算相同。 2、LIMIT 限制返回的行数。可以有两个参数,第一个参数为起始行,从 0 开始;第二个参数为返回的总行数。 返回前 5 行: SELECT * FROM myt…...
)
网络工程师应知应会:基础知识(5)
一、防火墙区域结构 防火墙按安全级别不同,可划分为内网、外网和 DMZ 区。 (1) 内网。 内网是防火墙的重点保护区域,包含单位网络内部的所有网络设备和主机。该区域是可信的,内网发出的连接较少进行过滤和审计。 (2) 外网。 外网是防火墙重…...

Minio多节点多驱动分布式部署官网文档翻译
原文链接: Deploy MinIO: Multi-Node Multi-Drive — MinIO Object Storage for Linux The procedures on this page cover deploying MinIO in a Multi-Node Multi-Drive (MNMD) or “Distributed” configuration. MNMD deployments provide enterprise-grade p…...
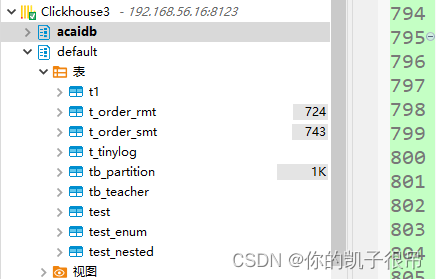
python连接clickhouse (CK)
Author: tkhywang 2810248865qq.com Date: 2023-11-01 11:28:58 LastEditors: tkhywang 2810248865qq.com LastEditTime: 2023-11-01 11:36:25 FilePath: \PythonProject02\Python读取clickhouse2 数据库数据.py Description: 这是默认设置,请设置customMade, 打开koroFileHead…...
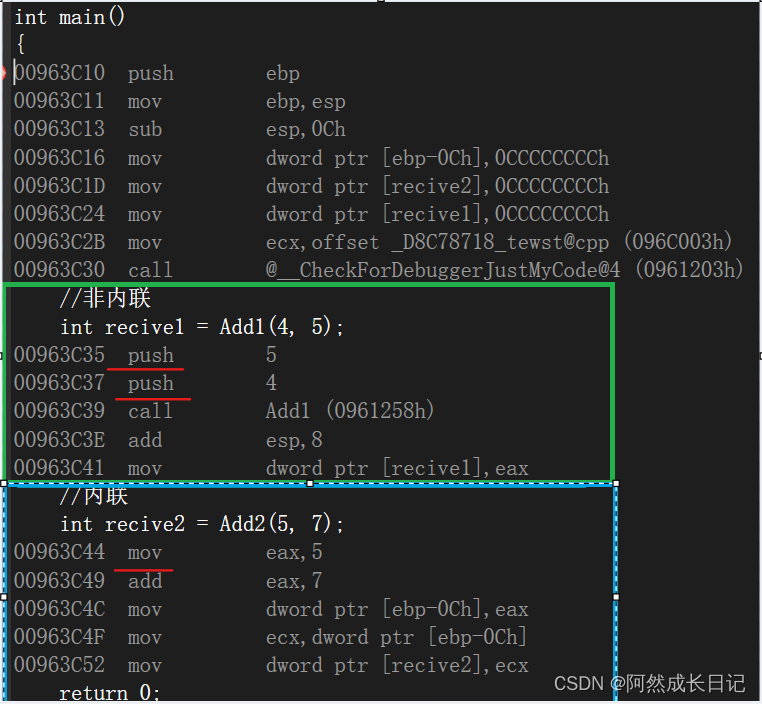
【C++】内联函数一看就懂?
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...

非洲“支付宝”PalmPay搭载OceanBase:成本降低80%
10 月 30 日,非洲支付公司PalmPay 的核心系统搭载国产自研数据库OceanBase,正式投入使用。PalmPay 也是 OceanBase 首个非洲商业用户。 作为一家非洲领先的金融科技公司,PalmPay 于 2019 年在尼日利亚推出电子钱包应用,其功能类似…...

EASYX图片操作
easyx学习网址 建议使用谷歌搜索引擎搜索相关的资料 eg1:图片显示到桌面 #include <stdio.h> #include <easyx.h> #include <iostream> #include <math.h> #include <stdlib.h> #include <conio.h> #include <time.h> #define PI 3…...

多测师肖sir_高级金牌讲师__adb命令
adb指令整理: ADB常用的指令: 查看当前连接设备 : adb devices 进入到shell : adb shell 查看日志 : adb logcat 安装apk文件 : adb install xxx.apk 卸载APP : adb uninstall 包名 查看包名 &…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
