【机器学习】正规方程与梯度下降API及案例预测
正规方程与梯度下降API及案例预测
文章目录
- 正规方程与梯度下降API及案例预测
- 1. 正规方程与梯度下降
- 正规方程(Normal Equation)
- 梯度下降(Gradient Descent)
- 2. API
- 3. 波士顿房价预测
1. 正规方程与梯度下降
回归模型是机器学习中用于预测连续数值(实数)的模型,通常用于解决回归问题。两种常见的回归模型求解方法是正规方程和梯度下降。
正规方程(Normal Equation)
正规方程是一种封闭解法,用于直接计算线性回归模型的权重(系数)。
原理:
给定一个线性回归模型的数据集,我们的目标是找到最佳的权重(系数)w,使得模型的预测值尽可能接近实际值。正规方程的原理是通过最小化损失函数来找到最佳权重。对于线性回归问题,损失函数通常是均方误差(Mean Squared Error):
J ( w ) = 1 2 m ∑ i = 1 m ( h w ( x ( i ) ) − y ( i ) ) 2 J(w) = \frac{1}{2m} \sum_{i=1}^{m} (h_w(x^{(i)}) - y^{(i)})^2 J(w)=2m1i=1∑m(hw(x(i))−y(i))2
其中,m 是训练样本数量,
h w ( x ( i ) ) h_w(x^{(i)}) hw(x(i))
是模型的预测值,
y ( i ) y^{(i)} y(i)
是实际值。
正规方程的目标是找到权重w,使损失函数J(w)最小化。通过求解损失函数的梯度等于零的方程,可以得到权重w的解析解:
∇ J ( w ) = 0 \nabla J(w) = 0 ∇J(w)=0
这个方程的解即为最佳权重w,从而得到线性回归模型。
优点:
- 正规方程提供了封闭解,不需要手动选择学习率或迭代次数。
- 适用于小型数据集,通常在特征数量较少时表现良好。
缺点:
- 对于大型数据集,计算复杂度高,需要计算特征矩阵的逆,时间复杂度较高。
- 不适用于非线性模型。
梯度下降(Gradient Descent)
梯度下降是一种迭代优化算法,用于调整模型的参数,使损失函数最小化。
原理:
梯度下降的核心思想是通过迭代来更新模型参数,使损失函数逐渐减小。对于线性回归,梯度下降的损失函数是均方误差(Mean Squared Error),目标是最小化这个损失函数。
梯度下降的迭代过程如下:
- 初始化权重w。
- 计算损失函数J(w)关于权重 w w w的梯度
∇ J ( w ) \nabla J(w) ∇J(w) - 更新权重w,通常按照以下规则更新:
w = w − α ∇ J ( w ) w = w - \alpha \nabla J(w) w=w−α∇J(w)
,其中α是学习率,控制每次更新的步长。 - 重复步骤2和3,直到满足停止条件(例如,达到最大迭代次数或损失函数收敛)。
梯度下降的关键是学习率α的选择,过大的学习率可能导致算法不收敛,过小的学习率可能导致收敛速度慢。
优点:
- 适用于大型数据集和高维特征,计算复杂度较低。
- 可以用于各种不同类型的模型和损失函数,包括非线性模型。
缺点:
- 需要手动选择学习率和迭代次数,选择不当可能导致收敛问题或性能下降。
- 对特征缩放和初始化敏感。
2. API
sklearn.linear_model.LinearRegression(fit_intercept=True)
- 通过正规方程优化
- fit_intercept:是否计算偏置
- LinearRegression.coef_:回归系数
- LinearRegression.intercept_:偏执
sklearn.linear_model.SGDRegressor(loss=“squared_loss”,fit_intercept=True,learning_rate=“invscaling”,eta0=0.01)
- SGDRegressor类实现了随机梯度下降学习,它支持不同的loss函数和正则化惩罚项来拟合线性回归模型
- loss:损失类型
- loss=“squared_loss”:普通最小二乘法
- fit_intercept:是否计算偏置
- learning_rate:string,optional
- 学习率填充
- “constant”:eta=eta0
- “optimal”:eta=1.0/(alpha*(t+t0))[default]
- “invscaling”:eta=eta0/pow(t,power_t),power_t存在父类之中
- 对于一个常数值的学习率来说,可以使用learning_rate=“constant”,并使用eta0来指定学习率
- SGDRegressor.coef_:回归系数
- SGDRegressor.intercept_:偏置
3. 波士顿房价预测
- 实例数量:506,属性数量:13数值型或类别墅,帮助预测的属性
- 属性信息:
- CRIM城镇人均犯罪率
- ZN占地面积超过2.5万平方英尺的住宅用地比例
- INDUS城镇非零售业务地区的比例
- CHAS查尔斯河虚拟变量(=1,如果土地在河边;否则是0)
- NOX一氧化氮浓度(每1000万份)
- RM平均每居民房数
- AGE在1940年之前建成的所有者占用单位的比例
- DIS与五个波士顿就业中心的加权距离
- RAD辐射状公路的可达性指数
- TAX每10000美元的全额物业税率
- PTRATIO城镇师生比例
- B 1000(Bk-0.63)^2其中Bk是城镇中的黑人比例
- LSTAT人口中地位较低人群的百分数
- MEDV以1000美元计算的自由住房的中位数
- 缺失属性值:无
流程:
- 获取数据集
- 划分数据集
- 特征工程:无量纲化处理–标准化
- 预估器流程,fit()–>模型:coef_,intercept_
- 模型评估
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegressiondef linear_demo():"""正规方程的方法对波士顿房价进行预测:return:"""# 1. 获取数据boston = load_boston()# 2. 划分数据集x_train, x_test, y_train,y_test = train_test_split(boston.data, boston.target, random_state= 22)# 3. 标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 4. 预估器estimator = LinearRegression()estimator.fit(x_train, y_train)# 5. 得出模型print("权重系数为:\n", estimator.coef_)print("偏置为:\n", estimator.intercept_)# 6. 模型评估y_predict = estimator.predict(x_test)print("y_predict:\n", y_predict)print("直接对比真实值和预测值:\n", y_test == y_predict)score = estimator.score(x_test, y_test)print("准确率为:\n", score)
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import SGDRegressordef linear_demo():"""梯度下降的方法对波士顿房价进行预测:return:"""# 1. 获取数据boston = load_boston()# 2. 划分数据集x_train, x_test, y_train,y_test = train_test_split(boston.data, boston.target, random_state= 22)# 3. 标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 4. 预估器estimator = SGDRegressor()estimator.fit(x_train, y_train)# 5. 得出模型print("权重系数为:\n", estimator.coef_)print("偏置为:\n", estimator.intercept_)# 6. 模型评估y_predict = estimator.predict(x_test)print("y_predict:\n", y_predict)print("直接对比真实值和预测值:\n", y_test == y_predict)score = estimator.score(x_test, y_test)print("准确率为:\n", score)
相关文章:

【机器学习】正规方程与梯度下降API及案例预测
正规方程与梯度下降API及案例预测 文章目录 正规方程与梯度下降API及案例预测1. 正规方程与梯度下降正规方程(Normal Equation)梯度下降(Gradient Descent) 2. API3. 波士顿房价预测 1. 正规方程与梯度下降 回归模型是机器学习中…...
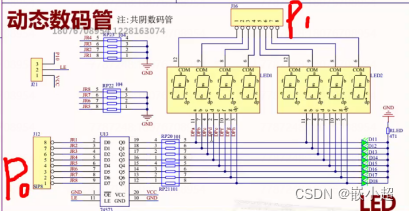
【SOC基础】单片机学习案例汇总 Part2:蜂鸣器、数码管显示
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...
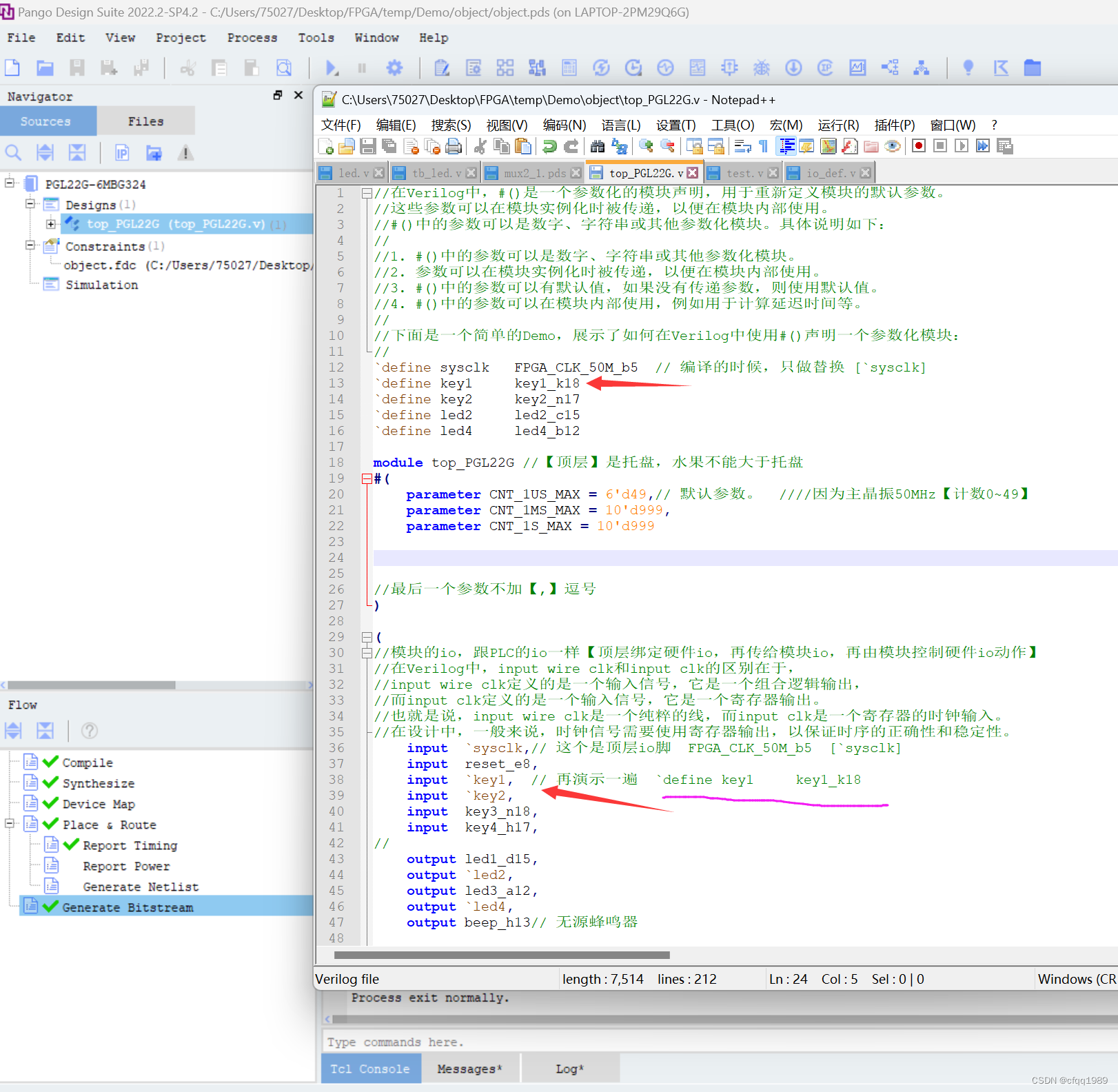
顶层模块【FPGA】
1顶层模块: 不能像C语言的h文件那样,把io的定义放在其他文件。 在Verilog中,顶层模块是整个设计的最高层次,它包含了所有其他模块和子模块。 顶层模块定义了整个设计的输入和输出端口,以及各个子模块之间的连接方式。…...

IT行业就业分析
1. IT技术发展背景及历程介绍 2. IT行业的就业方向有哪些? IT技术发展背景及历程介绍: IT技术的发展背景和历程可以追溯到上世纪40年代,以下是IT技术的主要发展阶段: 1.计算机的发展:二战期间,计算机作…...

读取用户剪贴板内容
读取用户剪贴板内容 在Web开发中,要读取用户剪贴板的内容,可以使用Clipboard API。这个API提供了一组方法和事件,用于访问和操作用户的剪贴板数据。 HTML <body><button onclick"readClipboard()">读取剪切板内容&l…...
“深入理解Nginx的负载均衡与动静分离“
目录 引言一、Nginx简介1. Nginx的基本概念2. Nginx的特点3. Nginx的安装配置 二、Nginx搭载负载均衡三、前端项目打包四、Nginx部署前后端分离项目,同时实现负载均衡和动静分离总结 引言 在现代互联网应用中,高性能和可扩展性是至关重要的。Nginx作为一…...
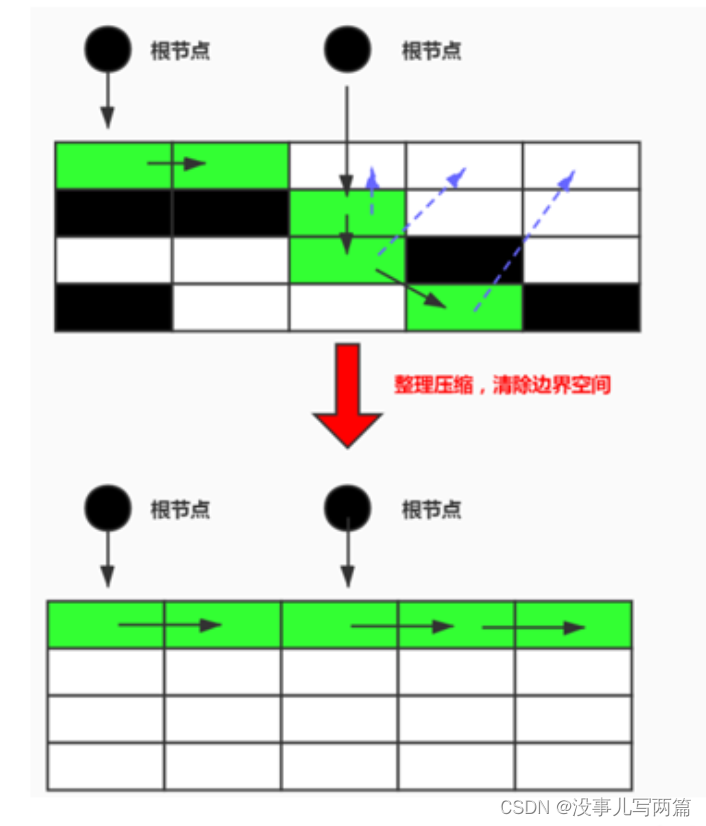
JVM 内存和 GC 算法
文章目录 内存布局直接内存执行引擎解释器JIT 即时编译器JIT 分类AOT 静态提前编译器(Ahead Of Time Compiler) GC什么是垃圾为什么要GC垃圾回收行为Java GC 主要关注的区域对象的 finalization 机制GC 相关算法引用计数算法(Reference Count…...
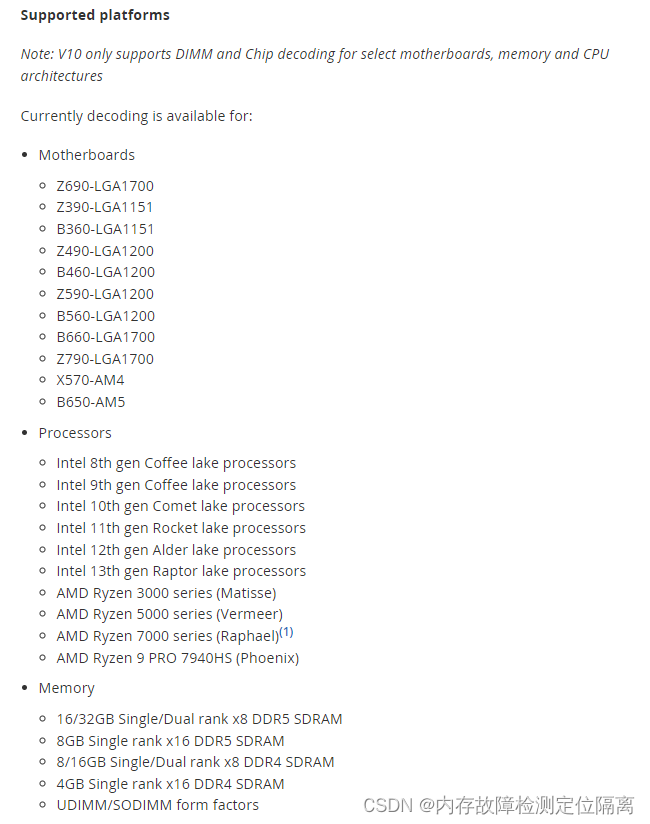
memtest86 prosite v10.6
passmark官方的memtest86 v10开始支持颗粒级别的坏内存芯片定位了,对于特定的若干种CPU和芯片组的组合,支持这项功能。 当然支持颗粒定位的site版本售价4800美金,是比较贵的。所以网络上出现了破解版的,人才真是。但是鼓励大家支…...

Springboot JSP项目如何以war、jar方式运行
文章目录 一,序二,样例代码1,代码结构2,完整代码备份 三,准备工作1. pom.xml 引入组件2. application.yml 指定jsp配置 四,war方式运行1. 修改pom.xml文件2. mvn执行打包 五,jar方式运行1. 修改…...

系统架构设计师(第二版)学习笔记----层次式架构设计理论与实践
【原文链接】系统架构设计师(第二版)学习笔记----层次式架构设计理论与实践 文章目录 一、层次式体系结构概述1.1 软件体系结构的作用1.2 常用的层次式架构图1.3 层次式体系可能存在的问题点 二、表现层框架设计2.1 MVC模式2.1.1 MVC三层模式2.1.2 MVC设…...
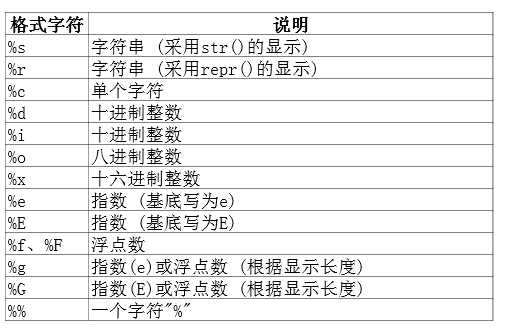
Python之字符串详解
目录 一、字符串1、转义字符与原始字符串2、使用%运算符进行格式化 一、字符串 在Python中,字符串属于不可变、有序序列,使用单引号、双引号、三单引号或三双引号作为定界符,并且不同的定界符之间可以互相嵌套。 ‘abc’、‘123’、‘中国’…...
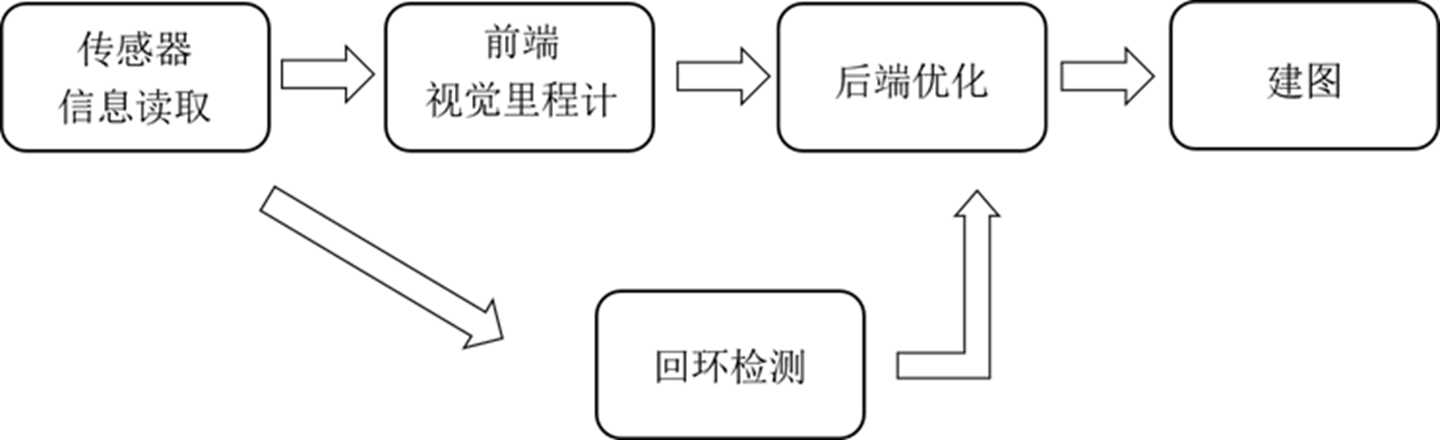
《视觉SLAM十四讲》-- 概述与预备知识
文章目录 01 概述与预备知识1.1 SLAM 是什么1.1.1 基本概念1.1.2 视觉 SLAM 框架1.1.3 SLAM 问题的数学表述 1.2 实践:编程基基础1.3 课后习题 01 概述与预备知识 1.1 SLAM 是什么 1.1.1 基本概念 (1)SLAM 是 Simultaneous Localization a…...

Java8 Stream API全面解析——高效流式编程的秘诀
文章目录 什么是 Stream Api?快速入门流的操作创建流中间操作filter 过滤map 数据转换flatMap 合并流distinct 去重sorted 排序limit 限流skip 跳过peek 操作 终结操作forEach 遍历forEachOrdered 有序遍历count 统计数量min 最小值max 最大值reduce 聚合collect 收集anyMatch…...
分享一下微信小程序里怎么开店
如何在微信小程序中成功开店:从选品到运营的全方位指南 一、引言 随着微信小程序的日益普及,越来越多的人开始尝试在微信小程序中开设自己的店铺。微信小程序具有便捷、易用、即用即走等特点,使得开店门槛大大降低。本文将详细介绍如何在微…...

uniapp小程序刮刮乐抽奖
使用canvas画布画出刮刮乐要被刮的图片,使用移动清除画布。 当前代码封装为刮刮乐的组件; vue代码: <template><view class"page" v-if"merchantInfo.cdn_static"><image class"bg" :src&q…...

Qt 窗口无法移出屏幕
1 使用场景 设计一个缩进/展开widget的效果,抽屉效果。 看到实现的方法有定时器里move窗口,或是使用QPropertyAnimation。 setWindowFlags(Qt::Dialog | Qt::FramelessWindowHint |Qt::X11BypassWindowManagerHint); 记得在移…...
java毕业设计基于springboot+vue线上教学辅助系统
项目介绍 本论文主要论述了如何使用JAVA语言开发一个线上教学辅助系统 ,本系统将严格按照软件开发流程进行各个阶段的工作,采用B/S架构,面向对象编程思想进行项目开发。在引言中,作者将论述线上教学辅助系统的当前背景以及系统开…...
开源 Wiki 软件 wiki.js
wiki.js简介 最强大、 可扩展的开源Wiki 软件。使用 Wiki.js 美观直观的界面让编写文档成为一种乐趣!根据 AGPL-v3 许可证发布。 官方网站:https://js.wiki/ 项目地址:https://github.com/requarks/wiki 主要特性: 随处安装&a…...
STM32基本定时器中断
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、STM32定时器的结构?1. 51定时器的结构1.1如何实现定时1s的功能? 2. stm32定时器的结构2.1 通用定时器 二、使用步骤1.开启时钟2.初始…...

学习历程_基础_精通部分_达到手搓的程度
1. 计算机网络(更新版) 1.1 计算机网络-43题 1.2 2. 操作系统(更新版) 3. ACM算法(更新版) 4. 数据库(更新版) 5. 业务开发算法(更新版) 6. 分布式类(更新版) 7. 设计模式(更新版ÿ…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
