《视觉SLAM十四讲》-- 概述与预备知识
文章目录
- 01 概述与预备知识
- 1.1 SLAM 是什么
- 1.1.1 基本概念
- 1.1.2 视觉 SLAM 框架
- 1.1.3 SLAM 问题的数学表述
- 1.2 实践:编程基基础
- 1.3 课后习题
01 概述与预备知识
1.1 SLAM 是什么
1.1.1 基本概念
(1)SLAM 是 Simultaneous Localization and Mapping 的缩写,即同时定位与地图构建。它是指搭载特定传感器的主体,在没有环境先验信息的情况下,于运动过程中建立环境的模型。
(2)两大基本问题:
-
定位:我在什么地方?
-
建图:周围环境是什么样的?
(3)准确的定位需要精确的地图,精确的地图来自准确的定位。
(4)传感器
-
内质的(放置在机器人身上,用于感受机器人本体信息):IMU(惯性测量单元)、激光、相机
-
外质的(安装于环境中,监测机器人的运动状态):二维码、GPS导轨
(5)相机
以一定速率采集图像,形成视频。相较于激光传感器更便宜,信息更丰富。
相机以二维投影形式记录三维世界的信息,丢掉了距离信息。
分类:
-
单目相机:最常见的普通相机
-
双目相机(立体相机):类似于人眼,通过视差计算出距离信息
-
深度相机(RGB-D):发射端、接收端,获得RGB图和深度图
-
其他:全景相机、事件相机
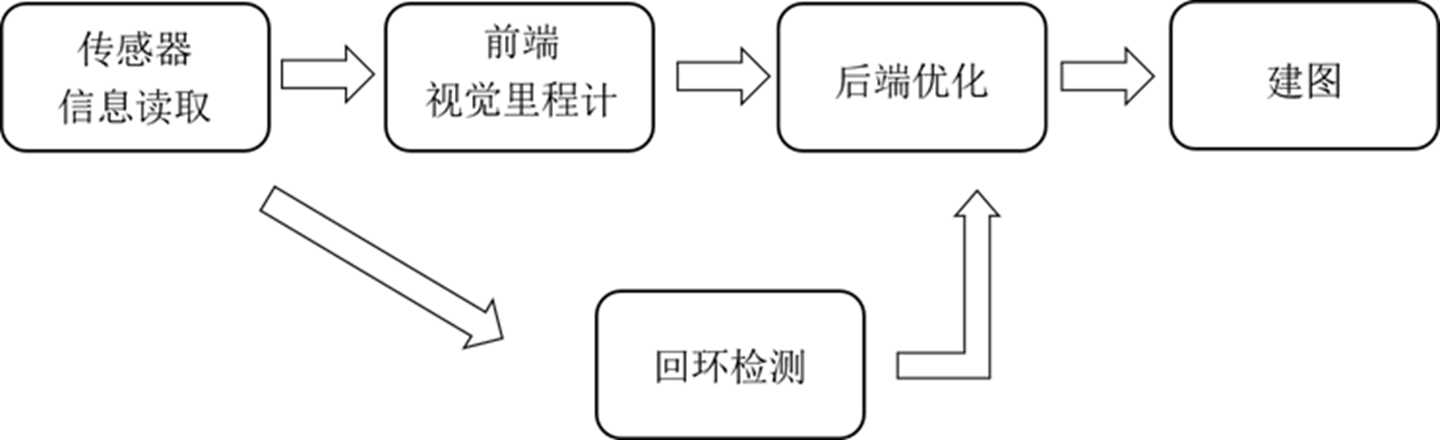
1.1.2 视觉 SLAM 框架
-
前端:Visual Odometry(VO),视觉里程计的任务是估算邻近时刻的相机运动。主要方法:特征点法、直接法
-
后端:Optimization,从带有噪声的数据中估计最优轨迹与地图。常用方法:最大后验估计、滤波器、图优化。
-
回环检测:Loop Closing,主要解决位置估计随时间漂移的问题。判断机器人是否到达过先前的位置,如果检测到回环,将信息提供给后端进行处理。
-
建图:Mapping,根据估计的轨迹,建立地图。主要分为度量地图和拓扑地图两类。度量地图又分为稀疏地图和稠密地图,稀疏地图比较抽象,仅包含一部分有意义的信息——地标。进行导航时,就需要稠密地图(避免碰撞某些障碍物)。
1.1.3 SLAM 问题的数学表述
(1)数学表述
两个方程:运动方程和观测方程
{ x k = f ( x k − 1 , u k , w k ) z k , j = h ( y j , x k , v k , j ) (1-1) \left\{ \begin{matrix} \boldsymbol{x_k}=f(\boldsymbol{x_{k-1}},\boldsymbol{u_k}, \boldsymbol{w_k}) \\ \boldsymbol{z_{k,j}}=h(\boldsymbol{y_j},\boldsymbol{x_k},\boldsymbol{v_{k,j}}) \end{matrix} \right. \tag{1-1} {xk=f(xk−1,uk,wk)zk,j=h(yj,xk,vk,j)(1-1)
这里, x k \boldsymbol{x_k} xk 为 k k k 时刻的位置, u k \boldsymbol{u_k} uk 是运动传感器的读数或输入,比如相对上一位置前进1 m 或左转 10°; w k \boldsymbol{w_k} wk 为噪声。 z k , j \boldsymbol{z_{k,j}} zk,j 为机器人在 x k \boldsymbol{x_k} xk 位置时对路标 y j \boldsymbol{y_j} yj 的观测数据, v k , j \boldsymbol{v_{k,j}} vk,j 为此次观测的噪声。
对于简单的平面运动,机器人的位姿由横纵坐标和转角组成 x k = [ x 1 , x 2 , θ ] T \boldsymbol{x_k}=[x_1, x_2, \theta ]^T xk=[x1,x2,θ]T,变化量 u k = [ Δ x 1 , Δ x 2 , Δ θ ] T \boldsymbol{u_k}=[\Delta x_1, \Delta x_2, \Delta\theta ]^T uk=[Δx1,Δx2,Δθ]T,则运动方程可简化为
[ x 1 x 2 θ ] k = [ x 1 x 2 θ ] k − 1 + [ Δ x 1 Δ x 2 Δ θ ] k + w k (1-2) \left[\begin{matrix} { x }_{ 1 } \\ { x }_{ 2 } \\ \theta \end{matrix}\right]_k = \left[\begin{matrix} { x }_{ 1 } \\ { x }_{ 2 } \\ \theta \end{matrix}\right]_{k-1} + \left[\begin{matrix} \Delta{ x }_{ 1 } \\\Delta{ x }_{ 2 } \\\Delta\theta \end{matrix}\right]_{k} + \boldsymbol{w_k} \tag{1-2} x1x2θ k= x1x2θ k−1+ Δx1Δx2Δθ k+wk(1-2)
对于观测方程,以激光传感器为例,可以测量出此位置和路标之间的距离 r r r 和夹角 ϕ \phi ϕ,路标点位置记为 y j = [ y 1 , y 2 ] T j \boldsymbol{y_j}=[y_1, y_2]^{T_j } yj=[y1,y2]Tj,位姿为 x k = [ x 1 , x 2 ] T j \boldsymbol{x_k}=[x_1, x_2]^{T_j } xk=[x1,x2]Tj ,观测数据为 z k , j = [ r k , j , ϕ k , j ] T \boldsymbol{z_{k,j}}=[r_{k,j}, \phi_{k,j}]^{T} zk,j=[rk,j,ϕk,j]T,在笛卡尔坐标系中,可以写为
[ r k , j ϕ k , j ] = [ ( y 1 , j − x 1 , k ) 2 + ( y 2 , j − x 2 , k ) 2 a r c t a n ( y 2 , j − x 2 , k ) ( y 1 , j − x 1 , k ) ] + v (1-3) \left[\begin{matrix} r_{k,j} \\\phi_{k,j} \end{matrix}\right] = \left[\begin{matrix} \sqrt{{(y_{1,j}}-x_{1,k})^2+{(y_{2,j}}-x_{2,k})^2} \\ arctan{ (y_{2,j}-x_{2,k}) \over (y_{1,j}-x_{1,k})} \end{matrix}\right] + \boldsymbol{v} \tag{1-3} [rk,jϕk,j]=[(y1,j−x1,k)2+(y2,j−x2,k)2arctan(y1,j−x1,k)(y2,j−x2,k)]+v(1-3)
当然,对于三维空间中的运动或其他形式传感器,上式有不同的参数化形式。
(2)SLAM 是一个状态估计问题
按运动和观测方程是否为线性,噪声是否符合高斯分布,分为线性/非线性和高斯/非高斯系统。
-
线性高斯系统: 卡尔曼滤波
-
非线性非高斯系统: 扩展卡尔曼滤波、非线性优化
1.2 实践:编程基基础
- Ubuntu 系统
- C++
- 编辑器:Clion、VS Code
- 工具:cmake
- 库:Eigen、G2O、Ceres、OpenCV等
1.3 课后习题
相关文章:

《视觉SLAM十四讲》-- 概述与预备知识
文章目录 01 概述与预备知识1.1 SLAM 是什么1.1.1 基本概念1.1.2 视觉 SLAM 框架1.1.3 SLAM 问题的数学表述 1.2 实践:编程基基础1.3 课后习题 01 概述与预备知识 1.1 SLAM 是什么 1.1.1 基本概念 (1)SLAM 是 Simultaneous Localization a…...

Java8 Stream API全面解析——高效流式编程的秘诀
文章目录 什么是 Stream Api?快速入门流的操作创建流中间操作filter 过滤map 数据转换flatMap 合并流distinct 去重sorted 排序limit 限流skip 跳过peek 操作 终结操作forEach 遍历forEachOrdered 有序遍历count 统计数量min 最小值max 最大值reduce 聚合collect 收集anyMatch…...
分享一下微信小程序里怎么开店
如何在微信小程序中成功开店:从选品到运营的全方位指南 一、引言 随着微信小程序的日益普及,越来越多的人开始尝试在微信小程序中开设自己的店铺。微信小程序具有便捷、易用、即用即走等特点,使得开店门槛大大降低。本文将详细介绍如何在微…...

uniapp小程序刮刮乐抽奖
使用canvas画布画出刮刮乐要被刮的图片,使用移动清除画布。 当前代码封装为刮刮乐的组件; vue代码: <template><view class"page" v-if"merchantInfo.cdn_static"><image class"bg" :src&q…...

Qt 窗口无法移出屏幕
1 使用场景 设计一个缩进/展开widget的效果,抽屉效果。 看到实现的方法有定时器里move窗口,或是使用QPropertyAnimation。 setWindowFlags(Qt::Dialog | Qt::FramelessWindowHint |Qt::X11BypassWindowManagerHint); 记得在移…...
java毕业设计基于springboot+vue线上教学辅助系统
项目介绍 本论文主要论述了如何使用JAVA语言开发一个线上教学辅助系统 ,本系统将严格按照软件开发流程进行各个阶段的工作,采用B/S架构,面向对象编程思想进行项目开发。在引言中,作者将论述线上教学辅助系统的当前背景以及系统开…...
开源 Wiki 软件 wiki.js
wiki.js简介 最强大、 可扩展的开源Wiki 软件。使用 Wiki.js 美观直观的界面让编写文档成为一种乐趣!根据 AGPL-v3 许可证发布。 官方网站:https://js.wiki/ 项目地址:https://github.com/requarks/wiki 主要特性: 随处安装&a…...
STM32基本定时器中断
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、STM32定时器的结构?1. 51定时器的结构1.1如何实现定时1s的功能? 2. stm32定时器的结构2.1 通用定时器 二、使用步骤1.开启时钟2.初始…...

学习历程_基础_精通部分_达到手搓的程度
1. 计算机网络(更新版) 1.1 计算机网络-43题 1.2 2. 操作系统(更新版) 3. ACM算法(更新版) 4. 数据库(更新版) 5. 业务开发算法(更新版) 6. 分布式类(更新版) 7. 设计模式(更新版ÿ…...

Redis中的List类型
目录 List类型的命令 lpush lpushx rpush lrange lpop rpop lindex linsert llen lrem ltrim lset 阻塞命令 阻塞命令的使用场景 1.针对一个非空的列表进行操作 2.针对一个空的列表进行操作 3.针对多个key进行操作. 内部编码 lisi类型的应用场景 存储(班级…...
3D模型格式转换工具HOOPS Exchange:如何将3D PDF转换为STEP格式?
3D CAD数据在制造、工程和设计等各个领域都扮演着重要的角色。为了促进不同软件应用程序之间的协作和互操作性,它通常以不同的格式进行交换。 HOOPS Exchange是一个强大的软件开发工具包,提供了处理和将3D CAD数据从一种格式转换为另一种格式的解决方案…...
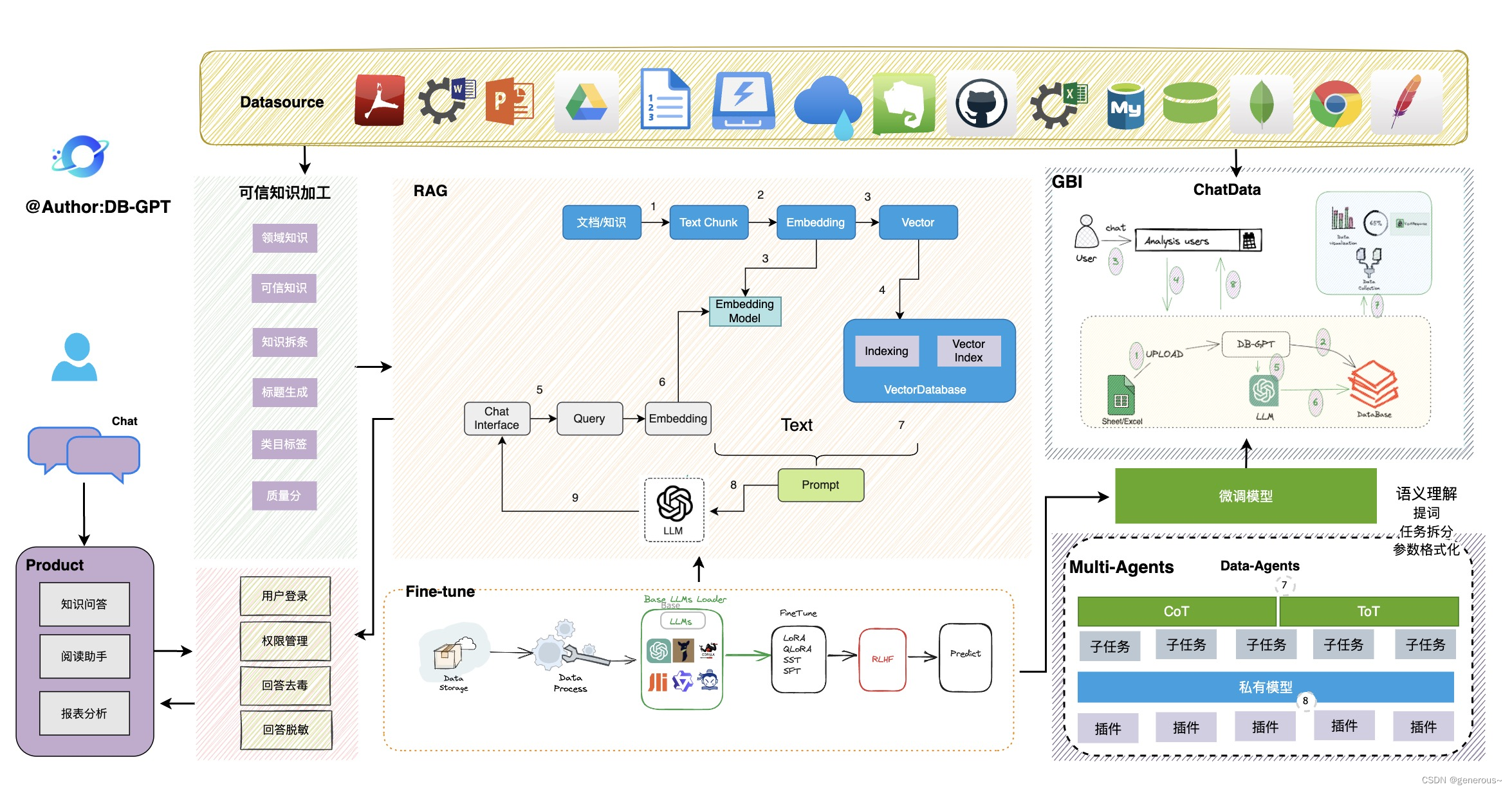
DB-GPT介绍
DB-GPT介绍 引言DB-GPT项目简介DB-GPT架构关键特性私域问答&数据处理多数据源&可视化自动化微调Multi-Agents&Plugins多模型支持与管理隐私安全支持数据源 子模块DB-GPT-Hub微调参考文献 引言 随着数据量的不断增长和数据分析的需求日益增多,将自然语言…...

Java,面向对象,内部类
内部类的定义: 将一个类A定义在另一个类B里面,里面的那个类A就称为内部类(InnerClass),类B则称为外部类(OuterClass)。 内部类的使用场景: 类A只在类B中使用,便可以使用内部类的方法…...

唯一ID如何生成,介绍一下目前技术领域最常使用的几种方法
纵使十面大山,又如何,无妨… 概述 唯一ID(Unique Identifier)是在计算机科学和信息技术领域中用于标识某个实体或数据的唯一标识符。生成唯一ID的方法可以根据具体需求和应用场景的不同而有所不同。以下是一些目前技术领域中常用…...
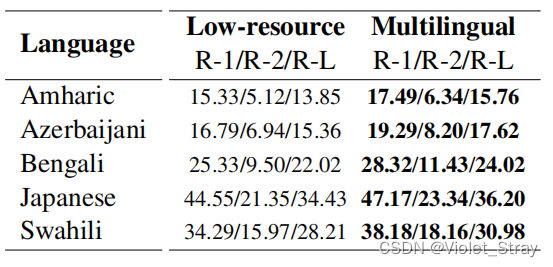
【翻译】XL-Sum: Large-Scale Multilingual Abstractive Summarization for 44 Languages
摘要 当代的关于抽象文本摘要的研究主要集中在高资源语言,比如英语,这主要是因为低/中资源语言的数据集有限。在这项工作中,我们提出了XL-Sum,这是一个包含100万篇专业注释的文章摘要对的综合多样数据集,从BBC中提取&…...
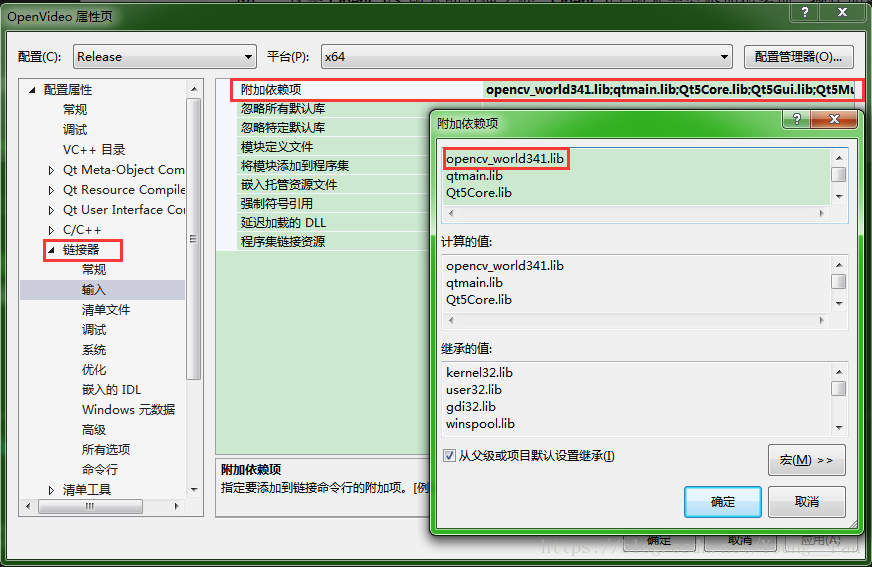
配置OpenCV
Open CV中包含很多图像处理的算法,因此学会正确使用Open CV也是人脸识别研究的一项重要工作。在 VS2017中应用Open CV,需要进行手动配置,下面给出在VS2017中配置Open CV的详细步骤。 1.下载并安装OpenCV3.4.1与VS2017的软件。 2.配置Open CV环…...

1-时间复杂度和空间复杂度
为了找到最适合当前问题而估量“算法”的评价s 时间复杂度空间复杂度执行效率:根据算法编写出的程序,执行时间越短,效率就越高占用的内存空间:不同算法编写出的程序,执行时占用的内存空间也不相同。如果实际场景中仅能…...

EtherCAT主站SOEM -- 3 -- SOEM之ethercatconfig.h/c文件解析
EtherCAT主站SOEM -- 3 -- SOEM之ethercatconfig.h/c文件解析 一 ethercatconfig.h/c文件功能预览:二 ethercatconfig.h/c 中主要函数的作用:2.1.1 ec_config_init(uint8 usetable) 和 ecx_config_init(ecx_contextt *context, uint8 usetable)ÿ…...

洗地机哪个品牌好?家用洗地机选购攻略
随着家用洗地机的普及和市场的广泛认可,进入洗地机行业的制造商也越来越多。在面对众多洗地机品牌时,消费者常常感到困惑,不知道如何选择。面对众多选择,选择有良好保障的知名洗地机品牌是明智之举。知名品牌在质量、售后服务等方…...
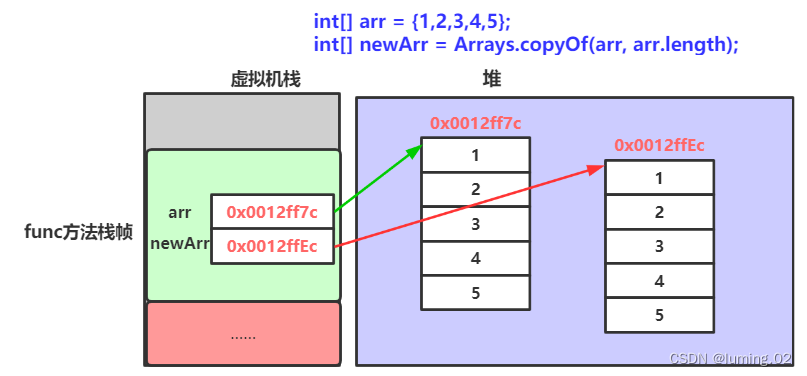
Java数组的定义与常用使用方法
目录 一.什么是数组 二.数组的创建及初始化 数组的创建 数组的初始化 动态初始化: 静态初始化: 【注意】 三.数组的使用 数组中元素访问 遍历数组 四.数组作为方法的参数 参数传基本数据类型 参数传数组类型(引用数据类型) 作为方法的返回…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...
