【算法】昂贵的聘礼(dijkstra算法)
题目
年轻的探险家来到了一个印第安部落里。
在那里他和酋长的女儿相爱了,于是便向酋长去求亲。
酋长要他用 10000 个金币作为聘礼才答应把女儿嫁给他。
探险家拿不出这么多金币,便请求酋长降低要求。
酋长说:”嗯,如果你能够替我弄到大祭司的皮袄,我可以只要 8000 金币。如果你能够弄来他的水晶球,那么只要 5000 金币就行了。”
探险家就跑到大祭司那里,向他要求皮袄或水晶球,大祭司要他用金币来换,或者替他弄来其他的东西,他可以降低价格。
探险家于是又跑到其他地方,其他人也提出了类似的要求,或者直接用金币换,或者找到其他东西就可以降低价格。
不过探险家没必要用多样东西去换一样东西,因为不会得到更低的价格。
探险家现在很需要你的帮忙,让他用最少的金币娶到自己的心上人。
另外他要告诉你的是,在这个部落里,等级观念十分森严。
地位差距超过一定限制的两个人之间不会进行任何形式的直接接触,包括交易。
他是一个外来人,所以可以不受这些限制。
但是如果他和某个地位较低的人进行了交易,地位较高的的人不会再和他交易,他们认为这样等于是间接接触,反过来也一样。
因此你需要在考虑所有的情况以后给他提供一个最好的方案。
为了方便起见,我们把所有的物品从 1 开始进行编号,酋长的允诺也看作一个物品,并且编号总是 1。
每个物品都有对应的价格 P,主人的地位等级 L,以及一系列的替代品 Ti 和该替代品所对应的”优惠” Vi。
如果两人地位等级差距超过了 M,就不能”间接交易”。
你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。
输入格式
输入第一行是两个整数 M,N,依次表示地位等级差距限制和物品的总数。
接下来按照编号从小到大依次给出了 N 个物品的描述。
每个物品的描述开头是三个非负整数 P、L、X,依次表示该物品的价格、主人的地位等级和替代品总数。
接下来 X 行每行包括两个整数 T 和 V,分别表示替代品的编号和”优惠价格”。
输出格式
输出最少需要的金币数。
数据范围
1 ≤ N ≤ 100
1 ≤ P ≤ 10000
1 ≤ L , M ≤ N
0 ≤ X < N
思路
我们可以根据以下样例绘制一张图:
样例:
1 4
10000 3 2
2 8000
3 5000
1000 2 1
4 200
3000 2 1
4 200
50 2 0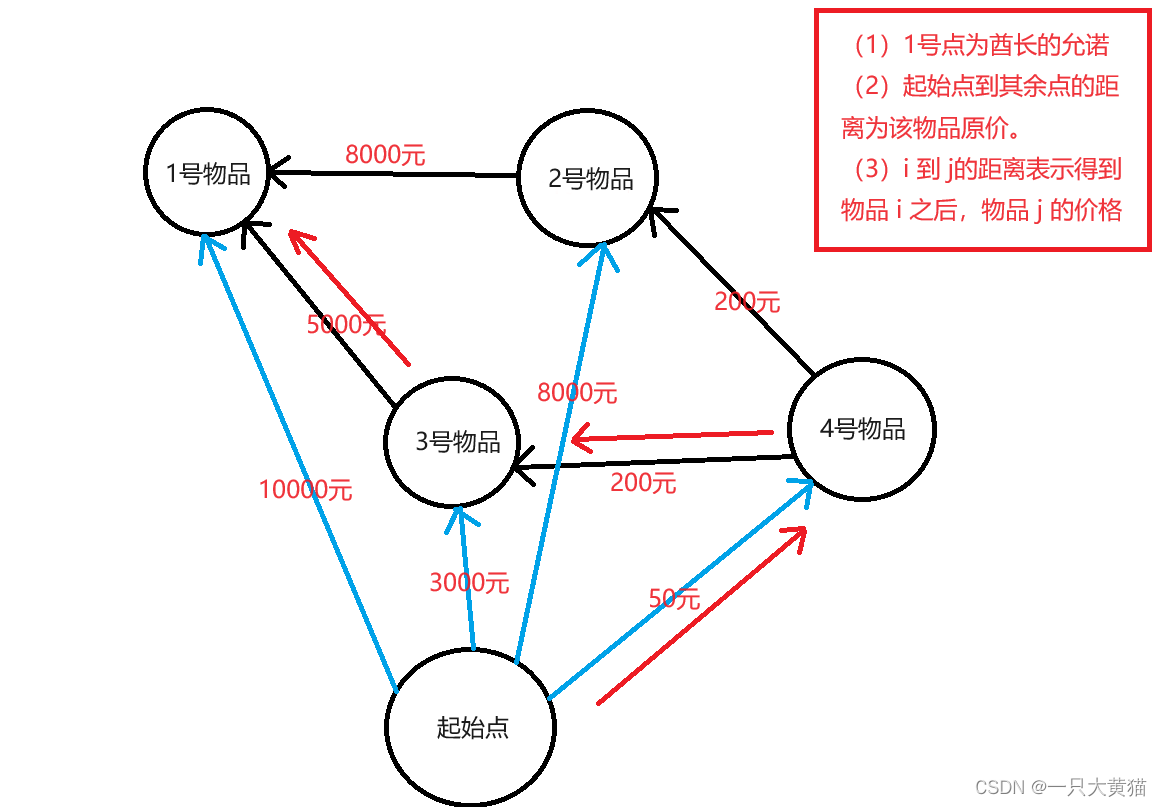
由图可知,我们可以反向建图,从起始点出发到达所有点的距离为物品 i 的原价,从点 i 到点 j 的距离为得到物品 i 之后物品 j 的价格。当我们建完图之后,很容易发现这个问题可以抽象成为一个最短路问题。
对于阶级问题:for(int i = level[ 1 ] - m; i <= level[ 1 ]; i ++) res = min(res,dijkstra(i, i + m)); i 表示可以交换的下界,i + m表示可以交换的上界 ,循环m次即可得到最小的花费。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 110,INF = 0x3f3f3f3f;
int n,m;// n等级差距限制,m物品个数
int w[N][N],level[N];//level数组储存的是第i个物品的主人所处的阶级,w数组储存点i到点j的边权
int dist[N];// 表示当前买到第i件物品价格的最小值
bool st[N];// 表示当前物品的价格是否为最小值int dijkstra(int down,int up)
{memset(dist,0x3f,sizeof(dist));// 将价格初始化为正无穷memset(st,0,sizeof(st));// 所有物品都没有确定最小价格dist[0] = 0;// 将起始点价格初始化为0int i = n;while(i --)// 循环n次确定n个物品的最小价格{int t = -1;// 在没有找到下一个可以确定价格已经最低的物品编号之前,t = -1for(int j = 0; j <= n; j ++)// 本次循环确定价格最小的物品编号if(!st[j] && (t == -1 || dist[t] > dist[j]))t = j;st[t] = true;// 该物品已经确定为最小价格,标记一下for(int j = 1; j <= n; j ++)// 使用这个已经确定最小价格的点对其他点进行更新if(level[j] >= down && level[j] <= up)// 如果阶级不符合条件,则不进行更新dist[j] = min(dist[j],dist[t] + w[t][j]);}return dist[1];
}int main()
{cin >> m >> n;// m等级差距限制,n物品总数memset(w,0x3f,sizeof(w));// 将数组w初始化for(int i = 1;i <= n; i ++) w[i][i] = 0;for(int i = 1;i <= n; i ++){int price,cnt;// price表示物品的价格,cnt表示替代品的数量cin >> price >> level[i] >> cnt;// 依次输入物品的价值,物品主人的阶级,代替品的数量w[0][i] = min(price,w[0][i]);// 起始点到该物品的距离(物品原价)while(cnt --){int id,cost;cin >> id >> cost;// 输入替代品的数量与价格w[id][i] = min(w[id][i],cost);//保留边权最小的值}}int res = INF;// 将答案初始化为正无穷for(int i = level[1] - m; i <= level[1]; i ++) res = min(res,dijkstra(i, i + m));// i表示可以交换的下界,i + m表示可以交换的上界cout << res << endl;return 0;}相关文章:

【算法】昂贵的聘礼(dijkstra算法)
题目 年轻的探险家来到了一个印第安部落里。 在那里他和酋长的女儿相爱了,于是便向酋长去求亲。 酋长要他用 10000 个金币作为聘礼才答应把女儿嫁给他。 探险家拿不出这么多金币,便请求酋长降低要求。 酋长说:”嗯,如果你能够替我…...
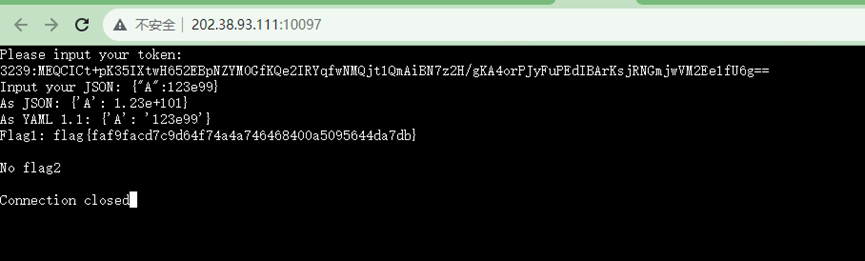
hackergame2023菜菜WP
文章目录 总结Hackergame2023更深更暗组委会模拟器猫咪小测标题HTTP集邮册Docker for everyone惜字如金 2.0Git? Git!高频率星球低带宽星球小型大语言模型星球旅行日记3.0JSON ⊂ YAML? 总结 最近看到科大在举办CTF比赛,刚好我学校也有可以参加,就玩了…...

ubuntu20.04.6使用FTP-及相关安全配置
前言: 作为一名运维,对文件系统,网络,文件共享,内存,CPU,以及一些应用服务及监控相关的知识需要 了解。今天是自己第一次搭建FTP(以前用过smb,windows共享,FT…...

C++中不允许复制的类
C中不允许复制的类 假设您需要模拟国家的政体。一个国家只能有一位总统,而 President 类面临如下风险: President ourPresident; DoSomething(ourPresident); // duplicate created in passing by value President clone; clone ourPresident; // dup…...
使用Python 脚自动化操作服务器配置
“ 有几十台特殊的服务器,没有合适的批量工具只能手动,要一个一个进行点击设置很耗费时间呀\~”,使用 Python 的简单脚本,即可模拟鼠标键盘进行批量作业 01 — 自动化示例 以某服务器中的添加用户权限为例,演示过程皆未触碰鼠标…...

DL Homework 6
目录 一、概念 (1)卷积 (2)卷积核 (3)特征图 (4)特征选择 (5)步长 (6)填充 (7)感受野 二、探究不同卷…...

软考高项论文-绩效域
干系人绩效域 预期目标指标及检查方法建立高效的工作关系干系人参与的连续性干系人认同项目目标变更的频率支持项目的干系人提高了满意度,并从中收益;反对项目的干系人没有对项目产生负面影响干系人行为干系人满意度干系人相关问题和风险团队绩效域 预期目标指标及检查方法共…...
设计模式之装饰模式--优雅的增强
目录 概述什么是装饰模式为什么使用装饰模式关键角色基本代码应用场景 版本迭代版本一版本二版本三—装饰模式 装饰模式中的巧妙之处1、被装饰对象和装饰对象共享相同的接口或父类2、当调用装饰器类的装饰方法时,会先调用被装饰对象的同名方法3、子类方法与父类方法…...
前端vue,后端springboot。如何防止未登录的用户直接浏览器输入地址访问
前端,使用Vue框架来实现前端路由拦截: 设置需要登录校验的页面: 登录成功后,去设置LocalStorage里面的IsLogin为true:...

linux安装Chrome跑web自动化
添加 Chrome 源: 打开终端并执行以下命令,将 Google Chrome 的 APT 源添加到系统: bashCopy code wget https://dl.google.com/linux/direct/google-chrome-stable_current_amd64.deb 安装 Chrome: 执行以下命令来安装 Chrome&…...

linux环境下编译,安卓平台使用的luajit库
一、下载luajit源码 1、linux下直接下载: a、使用curl下载:https://luajit.org/download/LuaJIT-2.1.0-beta3.tar.gz b、git下载地址;https://github.com/LuaJIT/LuaJIT.git 2、Windows下载好zip文件,下载地址:https…...

indexedDB笔记
indexedDB 该部分内容主要源于https://juejin.cn/post/7026900352968425486 常用场景:大量数据需要缓存在本地重要概念 仓库objectStore:类似于数据库中的表,数据存储媒介索引index:索引作为数据的标志量,可根据索引获…...

系统提示缺少或找不到emp.dll文件的详细解决方案
我今天打开一款《游戏》。然而,在游戏中遇到了一个非常棘手的问题:游戏报错找不到emp.dll,无法继续执行代码。这让我们非常苦恼,因为这个问题严重影响了我们的游戏体验。 在经过一番努力之后,我终于找到了4个解决方法,…...

Python实现自动化网页操作
1 准备 推荐使用Chrome浏览器 1.1 安装selenium程序包 激活虚拟环境,打开新的Terminal,输入以下代码: python -m pip install selenium 如下图所示,表示安装成功,版本为4.7.2 安装成功 关闭虚拟环境,打…...

03 矩阵与线性变换
矩阵与线性变换 线性变换如何用数值描述线性变换特殊的线性变换反过来看总结 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 线性变换 如果一个变换具有以下两个性质,我们就称它是线性的: 一是直线在变换后仍然保持为直线二是原点必须…...
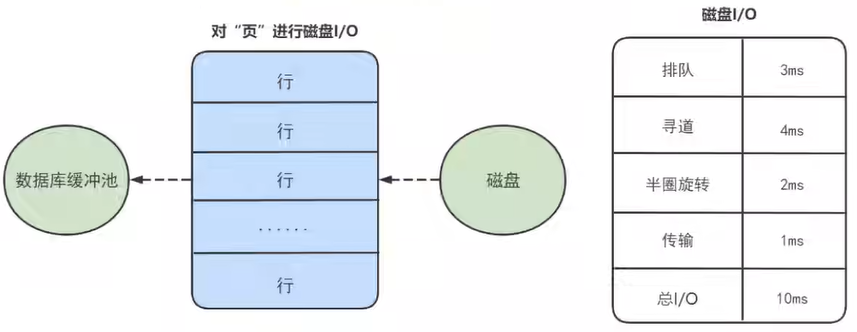
MySQL InnoDB数据存储结构
1. 数据库的存储结构:页 索引结构给我们提供了高效的索引方式,不过索引信息以及数据记录都是保存在文件上的,确切说是存储在页结构中。另一方面,索引是在存储引擎中实现的,MySQL服务器上的存储引擎负责对表中数据的读…...

【数据结构】数组和字符串(十五):字符串匹配2:KMP算法(Knuth-Morris-Pratt)
文章目录 4.3 字符串4.3.1 字符串的定义与存储4.3.2 字符串的基本操作4.3.3 模式匹配算法0. 朴素模式匹配算法1. ADL语言2. KMP算法分析3. 手动求失败函数定义例1例2例3 4. 自动求失败函数(C语言)5. KMP算法(C语言)6. 失败函数答案…...

STM32 PWM可控制电压原理
PWM可控制电压原理 主要通过PWM 输入模式根据控制单位时间内输出的平均电压,以调节电压大小。而PWM输出模式通过调节占空比,控制平均电压大小; 设置TIM为PWM输出模式 第一步:时钟使能: GPIO,TIM; 第二步&a…...

angular、 react、vue框架对比
借鉴:Web前端开发:三大主流框架 (baidu.com) AngularReactVue公司ChromeFaceBook尤雨溪写法有指令、模板的概念比较灵活,没有要求使用特定的架构和模式有指令和模板的概念性能低有虚拟Dom,性能高有虚拟Dome,性能高学习门槛 高&am…...

GNSS常用数据源汇总
本文整理汇总了GNSS数据处理过程中常用的数据源,路径中的占位符具体含义如下: -YYYY-年-YY-年的后两位数-DOY-年积日-MM-月-HH-小时-WWWW-GPS周 一、RINEXO观测值与RINEXN星历小时文件 1、CDDIS:ftp://gdc.cddis.eosdis.nasa.gov/pub/gnss…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
