【Java】汉诺塔
汉诺塔
汉诺塔(Tower of Hanoi)(河内塔):把圆盘从下面开始按大小顺序重新摆放到另一根柱子上,并且小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
汉诺塔规则
- disk表示圆盘数
- 一次只能移动一个圆盘
- 小圆盘只能在大圆盘的上方
- A 、B 、C分别表示圆柱
- A为起始圆柱、B为中转圆柱、C为终止圆柱
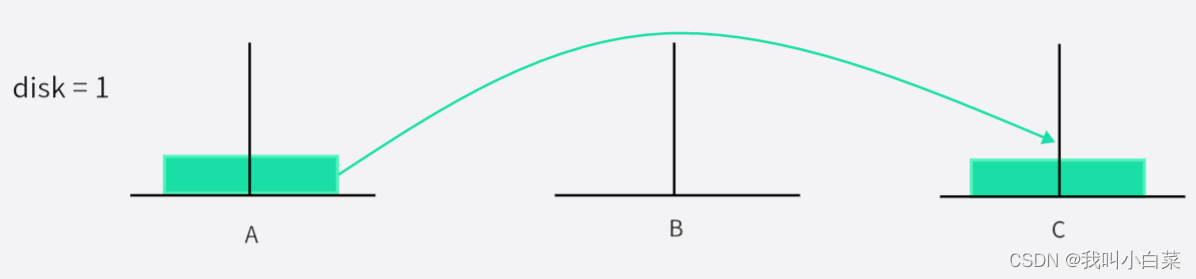
disk = 1 时:
移动次数为:2^1 - 1
只需要将绿色圆盘从 A->C 直接移过去;
A->C
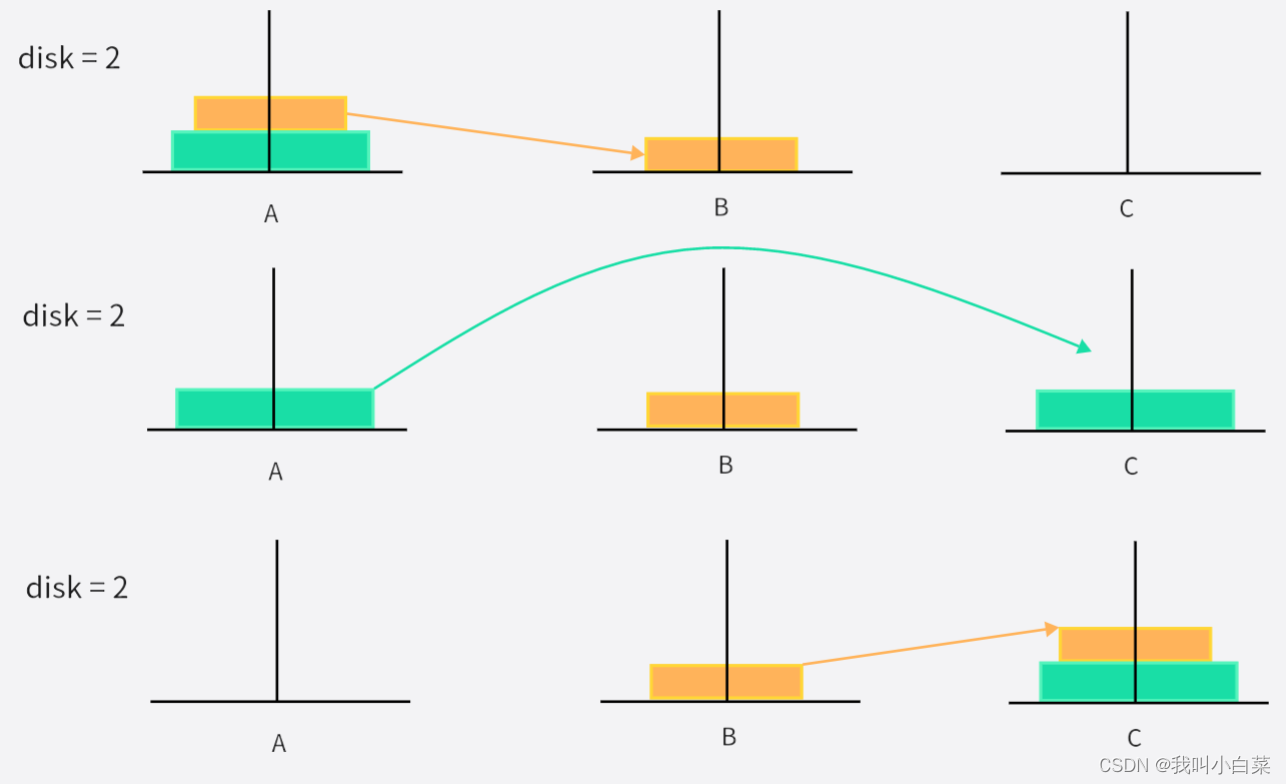
disk = 2 时:
移动次数为:2^2 - 1,一次只能移动一个圆盘
- 黄色圆盘从 A->B
- 绿色圆盘从 A->C
- 黄色圆盘从 B->C
A->B A->C B->C
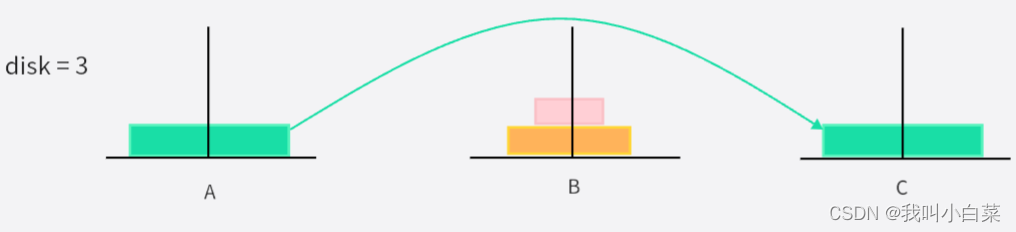
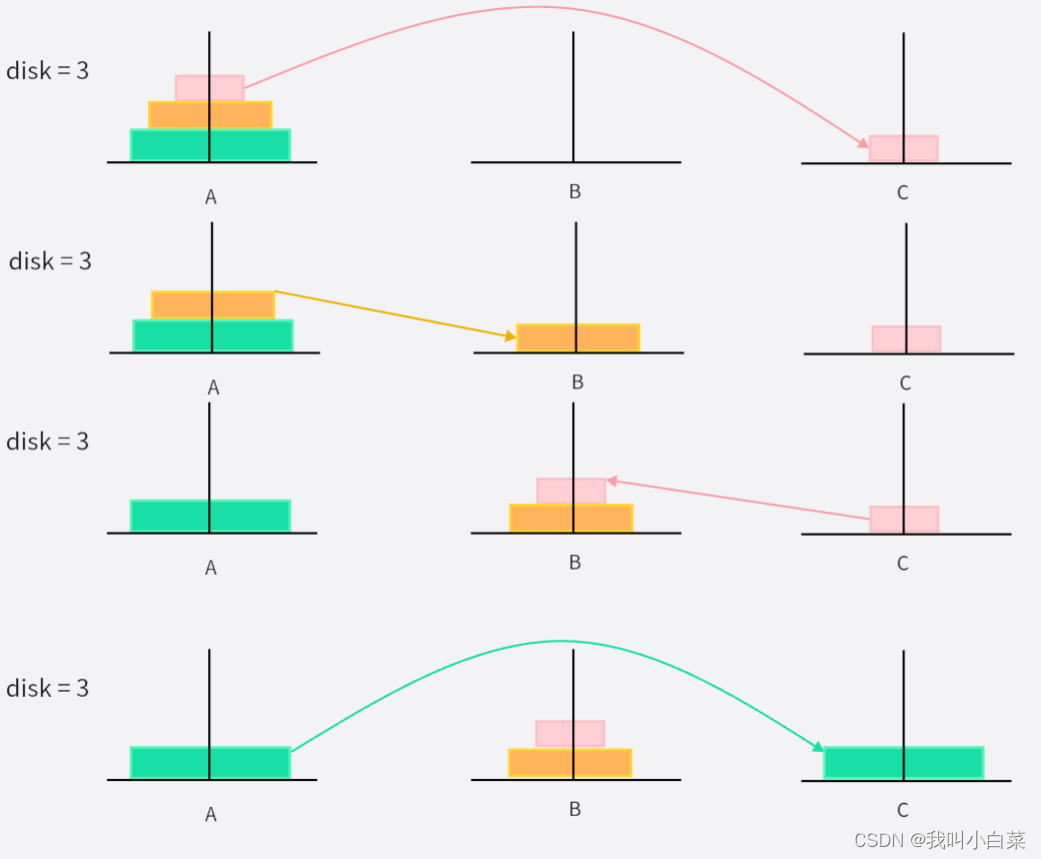
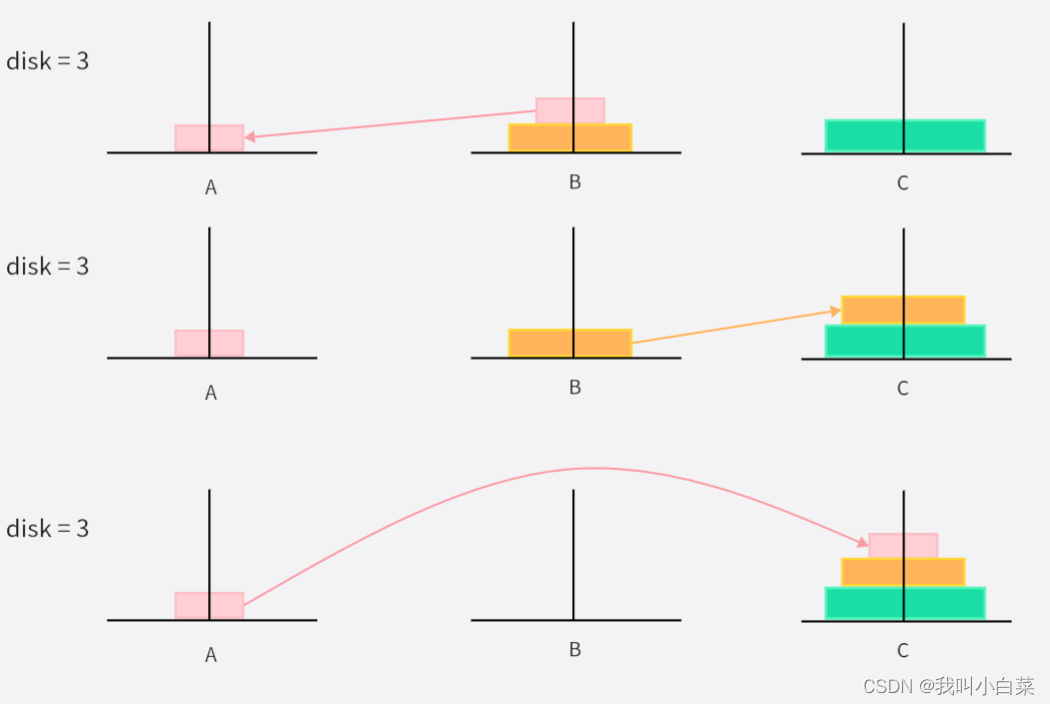
disk = 3 时:
移动次数为:2^3 - 1,一次只能移动一个圆盘
- 粉色圆盘从 A->C
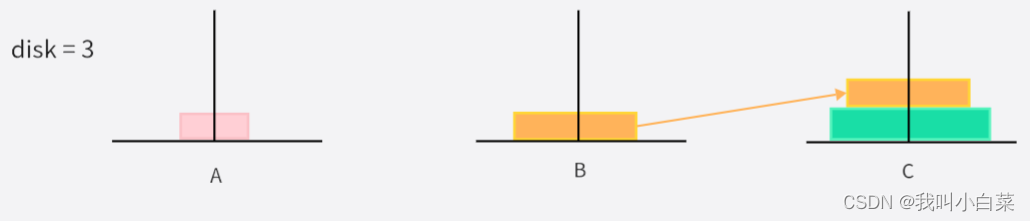
- 黄色圆盘从 A->B
- 粉色圆盘从 C->B
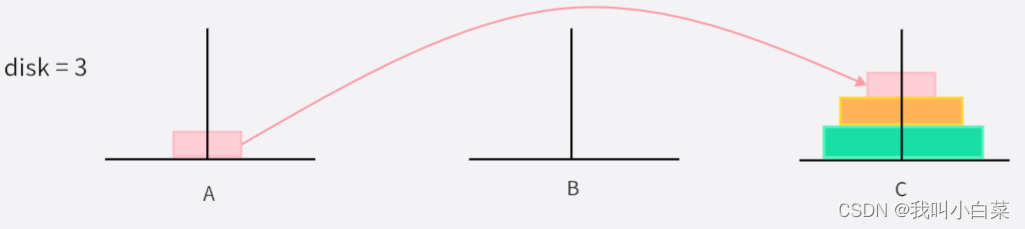
- 绿色圆盘从 A->C
- 粉色圆盘从 B->A
- 黄色圆盘从 B->C
- 粉色圆盘从 A->C
A->C A->B C->B A->C B->A B->C A->C
递归分析
- 先看desk = 3 个圆盘时,我们是先将圆柱A上面的2个圆盘(3 - 1),借助圆柱C最终移动到圆柱B上;
- 此时圆柱A上就只剩1个圆盘,就可以直接将圆盘从圆柱A移动到圆柱C;
- desk = 2个圆盘,先将圆柱B上面的那1个圆盘(2 - 1),最终直接从圆柱B移动到圆柱A上;
- 此时圆柱B上就只剩1个圆盘,就可以直接从圆柱B移动到圆柱C上;
- 只剩最后1个圆盘了,则是直接从圆柱A上移动到圆柱C上;
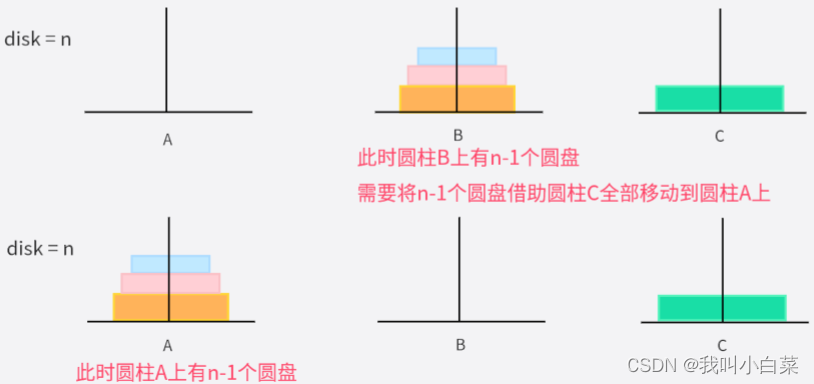
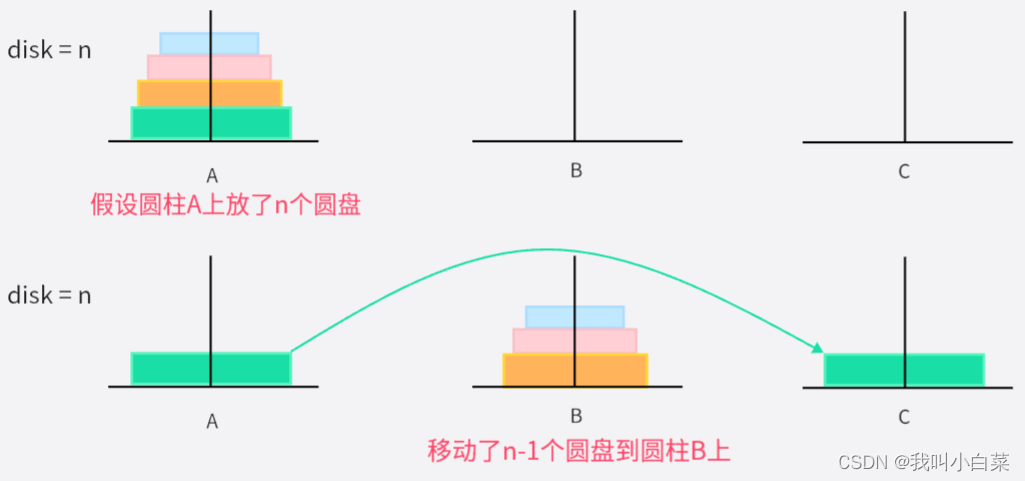
disk = n 时:
移动次数为:2^n - 1,一次只能移动一个圆盘
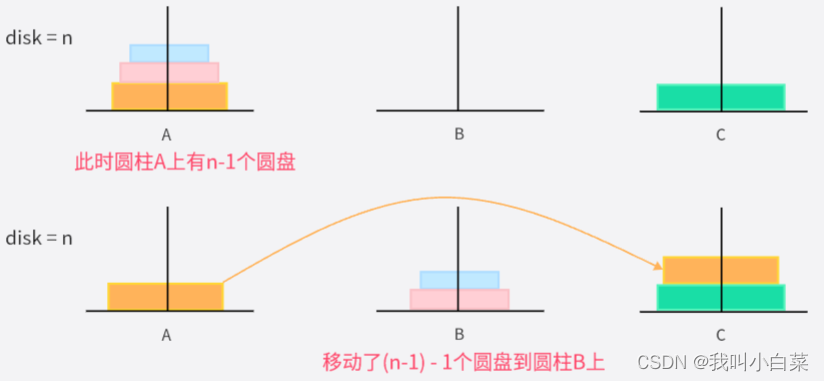
错误递归分析
- 当desk = n个圆盘时,需要将圆柱A上面的n-1个圆盘,借助圆柱C最终移动到圆柱B上;
- 此时圆柱A上就只剩1个圆盘,则直接从圆柱A移动到圆柱C;
- desk = n 时,先将圆柱B上面的n-1个圆盘,借助圆柱C最终移到圆柱A上;
- 此时圆柱A上有n-1个圆盘,递归以上步骤;
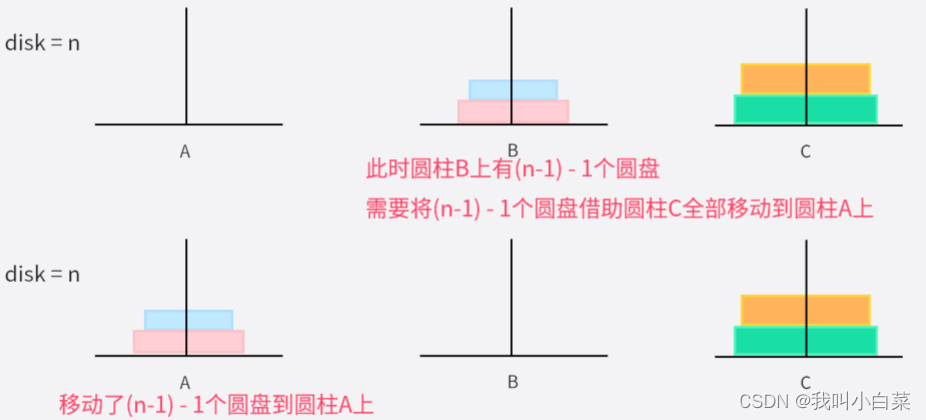
- 当 desk = n-1时,需要将圆柱A上面的(n-1) - 1个圆盘,借助圆柱C移到圆柱B上(这里已经在开始和desk = n 的情况一样);
- 此时圆柱A上就只剩1个圆盘,则直接从圆柱A移动到圆柱C;
- desk = n-1时,先将圆柱B上面的(n-1) - 1个圆盘,借助圆柱C最终移到圆柱A上;
- 此时圆柱A上有(n-1) - 1个圆盘,递归以上步骤;
错误代码分析
public class TowerOfHanoi {public static void hanoi(int n, char posA, char posB, char posC) {// hanoi(圆盘个数,参数1,参数2,参数3)// 参数1表示起始位置、参数2表示中转位置、参数3表示终止位置if(n == 1) {move(posA, posC);return; // 递归一定要return}// 这一步就是将 圆柱A 上的 n-1个 圆盘// 借助圆柱C 移动到 圆柱B上hanoi(n-1, posA, posC, posB);// 将圆柱A上剩下的一个移到圆柱C上move(posA, posC);// 将 圆柱B 上的所有圆盘 借助圆柱C 移到圆柱A上hanoi(n-1, posB, posC, posA); // 这里是错的}public static void move(char pos1, char pos2) {System.out.println(pos1 + "->" + pos2);}public static void main(String[] args) {hanoi(3, 'A', 'B', 'C');}
}正确递归分析
- 当desk = n个圆盘时,需要将圆柱A上面的n-1个圆盘,借助圆柱C最终移动到圆柱B上;
- 此时圆柱A上就只剩1个圆盘,则直接从圆柱A移动到圆柱C;
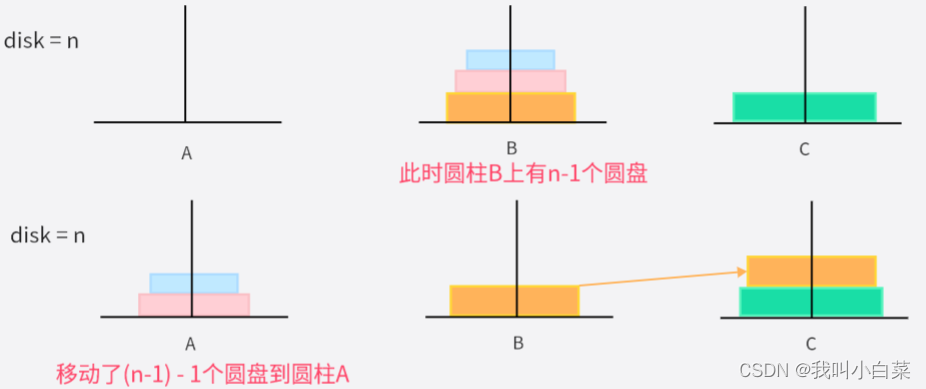
- 将圆柱B上的n-1个圆盘,借助圆柱A最终移动到圆柱C上;
- 此时圆柱B上就只剩一个圆盘,则直接从圆柱B移动到圆柱C;
正确代码分析
public class TowerOfHanoi {public static void hanoi(int n, char posA, char posB, char posC) {// hanoi(圆盘个数,参数1,参数2,参数3)// 参数1表示起始位置、参数2表示中转位置、参数3表示终止位置if(n == 1) {move(posA, posC);return; // 递归一定要return}// 这一步就是将 圆柱A 上的 n-1个 圆盘// 借助圆柱C 移动到 圆柱B上hanoi(n-1, posA, posC, posB);// 将圆柱A上剩下的一个移到圆柱C上move(posA, posC);hanoi(n-1, posB, posA, posC);}public static void move(char pos1, char pos2) {System.out.println(pos1 + "->" + pos2);}public static void main(String[] args) {hanoi(3, 'A', 'B', 'C');}
}相关文章:

【Java】汉诺塔
汉诺塔 汉诺塔(Tower of Hanoi)(河内塔):把圆盘从下面开始按大小顺序重新摆放到另一根柱子上,并且小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。 汉诺塔规则 disk表示圆盘数一次只…...
Java实现对Html文本的处理
1.引入jsoup <dependency><groupId>org.jsoup</groupId><artifactId>jsoup</artifactId><version>1.8.3</version> </dependency> 2. html示例 示例代码: <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1…...

Vue项目创建与启动(2023超详细的图文教程)
目录 一、下载node.js 二、下载vue-cli与webpack插件 三、项目初始化(项目配置详细信息) 四、项目启动 五、Vue项目工程结构(扩展知识) 一、下载node.js 1.检测是否已经安装过node.js 打开控制台,输入 npm -v如果有会显示对应版本 如果没有会显示…...
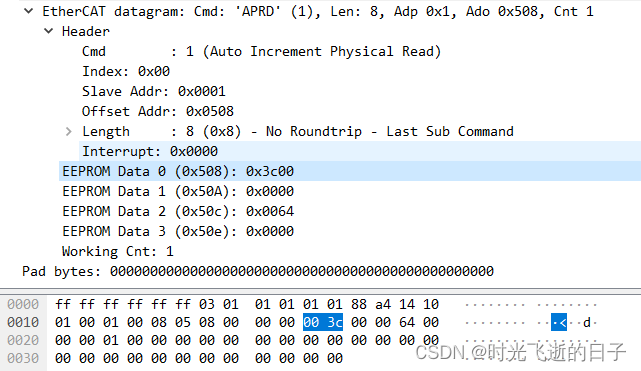
EtherCAT主站读取从站EEPROM抓包分析
0 工具准备 1.EtherCAT主站 2.EtherCAT从站(本文使用步进电机驱动器) 3.Wireshark1 抓包分析 1.1 报文总览 本文让主站去读取从站1字地址为0的EEPROM数据内容,主站读取从站EEPROM数据内容使用Wireshark抓包如下: 1.2 EEPROM读…...

Elasticsearch 8.X 如何生成 TB 级的测试数据 ?
1、实战问题 我只想插入大量的测试数据,不是想测试性能,有没有自动办法生成TB级别的测试数据?有工具?还是说有测试数据集之类的东西?——问题来源于 Elasticsearch 中文社区https://elasticsearch.cn/question/13129 2…...
汽车标定技术(四)--问题分析:多周期测量时上位机显示异常
目录 1.问题现象 2.数据流分析 3.代码分析 3.1 AllocDAQ 3.2 AllocOdt 3.3 AllocOdtEntry 4.根因分析及解决方法 4.1 根因分析 4.2 解决方案 1.问题现象 在手撸XCP代码时, DAQ的实现是一大头痛的事情。最初单周期实现还好一点,特别是…...
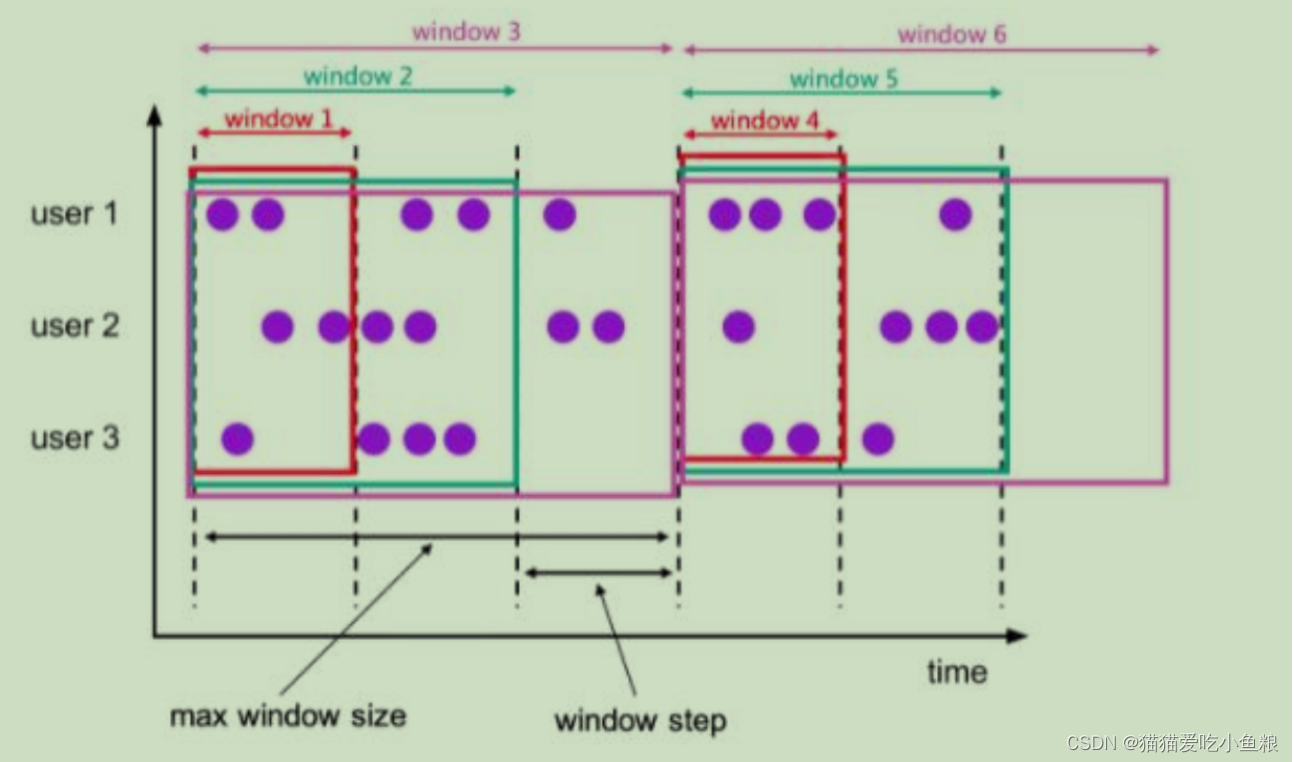
Flink SQL时间属性和窗口介绍
(1)概述 时间属性(time attributes),其实就是每个表模式结构(schema)的一部分。它可以在创建表的 DDL 里直接定义为一个字段,也可以在 DataStream 转换成表时定义。 一旦定义了时间…...
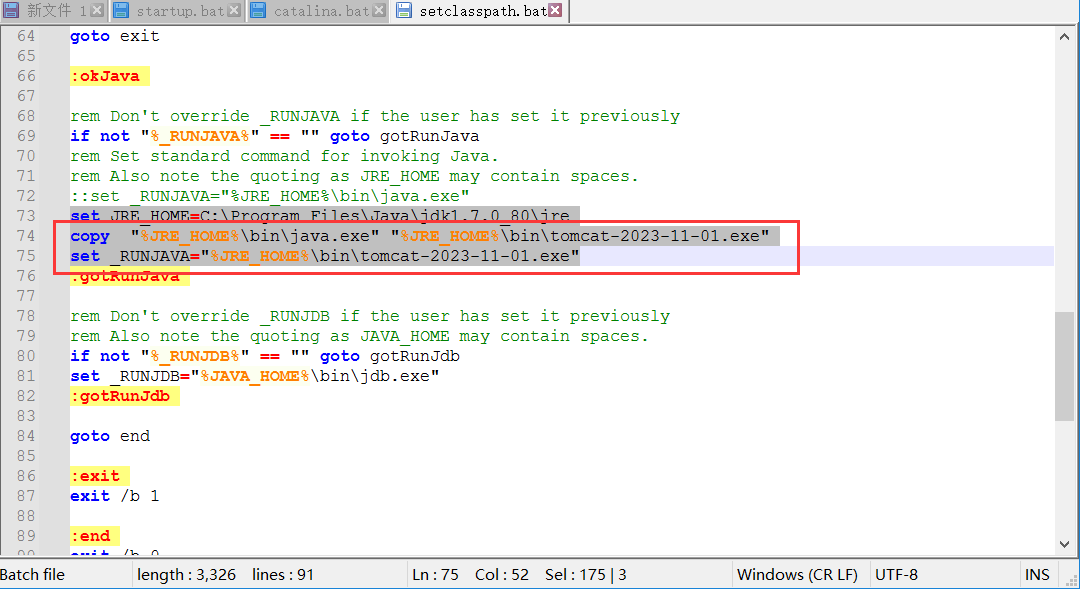
Tomcat免安装版修改标题名称和进程
tomcat免安装版启动后闪退问题 问题描述 在官网下载的tomcat免安装版的你安装完环境后发现启动闪退,tomcat启动依赖环境是JDK,所以需要tomcat对应版本的JDK支持。 tomcat8官网下载地址:https://tomcat.apache.org/ JDK环境官网下载地址&…...

vim搜索、替换tab
bibtex 中的缩进可能不一致,强迫症犯了想将: 缩进空格改 tab;行首的多个 tab 改为单个 参考 [1],空格换 tab 可以: :set noexpandtab :%retab!行首的多个 tab 换单个: :%s/^\t\/\t/gReferences Replac…...

一文读懂ARM安全性架构和可信系统构建要素
一文读懂ARM安全性架构和可信系统构建要素 所谓可信系统(trusted system),即能够用于保护密码和加密密钥等资产(assets)免受一系列的可信攻击,防止其被复制、损坏或不可用(unavailable…...
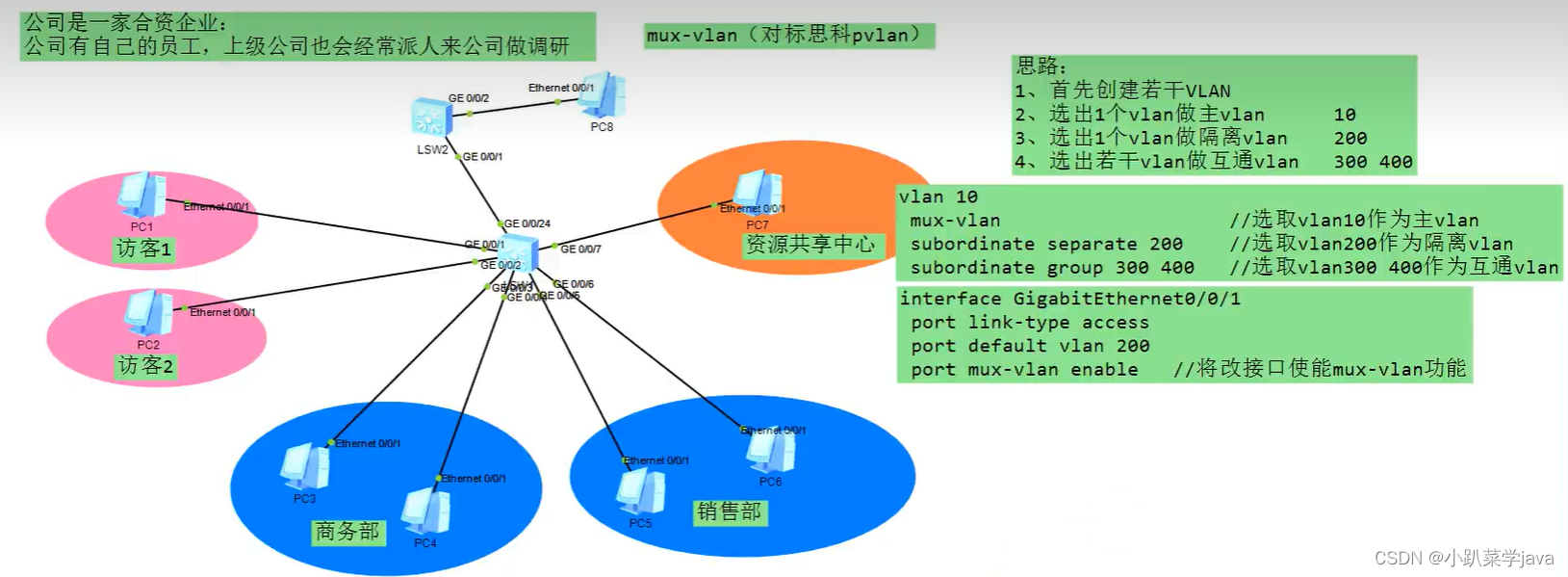
Voice vlan、ICMP、单臂路由、mux-vlan
目录 一,Voice VLAN Voice vlan配置命令 一,问:已知网络中一台服务器的IP地址,如何找到这太服务器在哪台交换机的哪个接口上编辑 思路: 二,ICMP协议 三,ICMP案例分析编辑 四…...
 理解select和epoll的使用)
TCP IP 网络编程(七) 理解select和epoll的使用
文章目录 理解select函数select函数的功能和调用顺序设置文件描述符设置监视范围及超时select函数调用示例 优于select的epoll基于select的I/O复用速度慢实现epoll时必要的函数和结构体epoll_createepoll_ctlepoll_wait基于epoll的服务器端 边缘触发和水平触发 理解select函数 …...

Linux accept和FD_xxx的使用
Linux socket accept功能的作用是在服务器端等待并接受客户端的连接请求。当有客户端尝试连接服务器时,服务器调用accept函数来接受该连接请求,并创建一个新的socket来与该客户端进行通信。 具体来说,accept函数被动监听客户端的三次握手连接…...
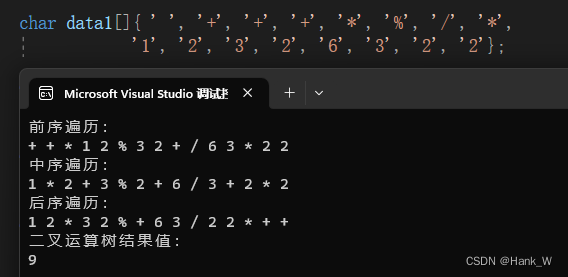
树结构及其算法-二叉运算树
目录 树结构及其算法-二叉运算树 C代码 树结构及其算法-二叉运算树 二叉树的应用实际上相当广泛,例如表达式之间的转换。可以把中序表达式按运算符优先级的顺序建成一棵二叉运算树(Binary Expression Tree,或称为二叉表达式树)…...

vue的rules验证失效,部分可以部分又失效的原因
vue的rules验证失效,部分可以部分又失效的原因 很多百度都有,但是我这里遇到了一个特别的,那就是prop没有写全,导致验证某一个失效 例子: 正常写法 el-form-item....多个省略<el-form-item label"胶币" prop"cost"><el-input v-model"form.…...

c#字符串转整数类型
将字符串转换为整数类型。为了方便,C#提供了一个内置的方法TryParse来实现这个功能 字符串(String):表示一串字符的数据类型。整数(Integer):表示不带小数点的数字。解析(Parsing&a…...

【LeetCode】118. 杨辉三角
118. 杨辉三角 难度:简单 题目 给定一个非负整数 *numRows,*生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 示例 1: 输入: numRows 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]示例…...
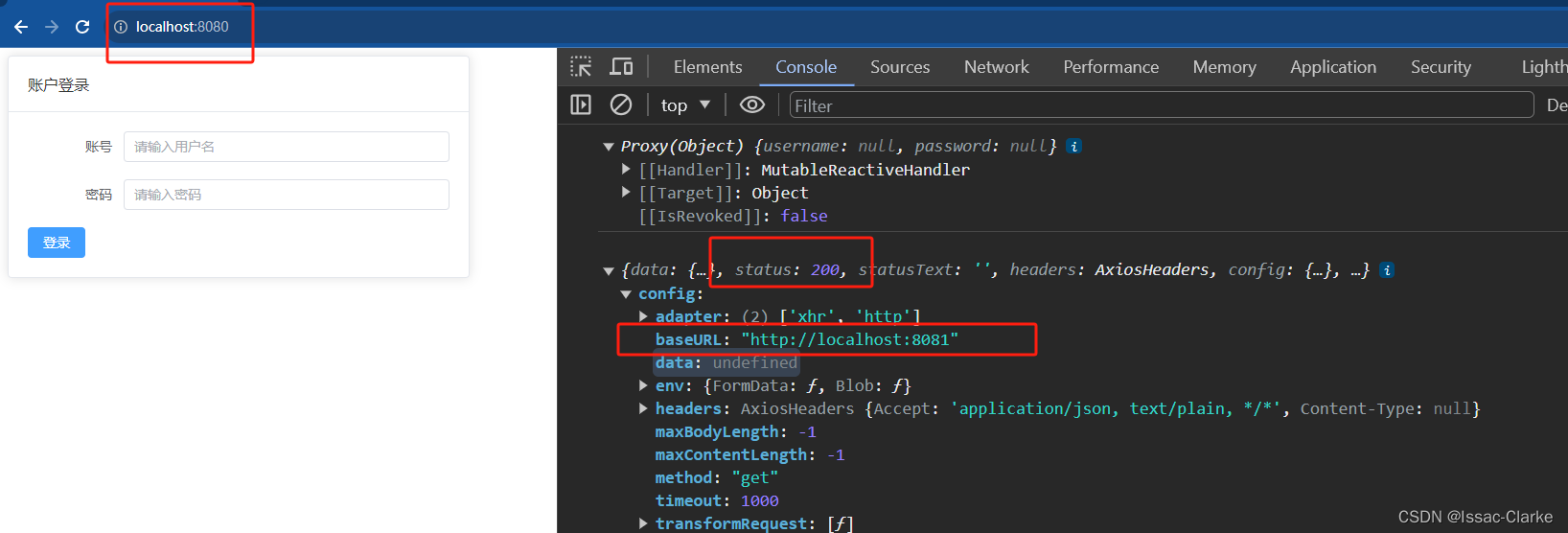
【Vue.js】Vue3全局配置Axios并解决跨域请求问题
系列文章目录 文章目录 系列文章目录背景一、部署Axios1. npm 安装 axios2. 创建 request.js,创建axios实例3. 在main.js中全局注册axios4. 在页面中使用axios 二、后端解决跨域请求问题方法一 解决单Contoller跨域访问方法二 全局解决跨域问题 背景 对于前后端分离…...

【车载开发系列】CRC循环冗余校验码原理
【车载开发系列】CRC循环冗余校验码原理 CRC循环冗余校验码原理 【车载开发系列】CRC循环冗余校验码原理一. CRC算法原理二. 生成多项式三. 多项式与其对应代码四. CRC码校验原理1)发送端2)接收端 五. CRC码原理方法1)发送端生成CRC码方法2&a…...
数据库实验:SQL的数据更新
目录 实验目的实验内容实验要求实验步骤实验过程总结 再次书接上文,sql基础的增删改查 实验目的 (1) 掌握DBMS的数据查询功能 (2) 掌握SQL语言的数据更新功能 实验内容 (1) update 语句用于对表进行更新 (2) delete 语句用于对表进行删除 (3) insert 语句用于对表…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...