《向量数据库指南》——用了解向量数据库Milvus Cloud搭建高效推荐系统
了解向量数据库
ANN 搜索是关系型数据库无法提供的功能。关系型数据库只能用于处理具有预定义结构、可直接比较值的表格型数据。因此,关系数据库索引也是基于这一点来比较数据。但是 Embedding 向量无法通过这种方式直接相互比较。因为我们不知道向量中的每个值代表什么意思,无法使用关系型数据库来确定一个向量是否一定小于另一个向量,唯一能做的就是计算两个向量之间的距离。

如果两个向量之间的距离很小,可以假设它们所代表的特征相似;如果距离很大,可以假设它们代表的数据十分不同。对我们而言,向量距离及其含义是有用的。我们可以创建索引结构,高效搜索这些数据。但是为向量数据构建索引也有不小挑战:计算两个向量间距离成本高昂,而且向量索引一旦构建完成后,不易于修改。因此,我们无法直接使用传统的关系型数据库来处理向量数据,需要使用专为向量数据而打造的向量数据库。
Milvus 是一款专为向量数据处理而设计的向量数据库,可以解决传统关系型数据库无法处理向量的问题,为海量向量数据高效构建索引。为了满足云原生的要求,Milvus 将计算和存储以及不同的计算任务(查询、数据处理和索引)分离开来。用户可以根据不同的应用灵活扩展每个组件。无论是数据插入密集型应用还是搜索密集型应用, Milvus 都能够轻松应对。如果有大量插入请求涌入,用户可以临时水平和垂直扩展索引节点以处理数据。同样,如果没有大量插入数据,但有大量搜索操作,用户可以减少索引节点的数量,并提高查询节点的吞吐量。Milvus 的系统架构设计(见图2
相关文章:

《向量数据库指南》——用了解向量数据库Milvus Cloud搭建高效推荐系统
了解向量数据库 ANN 搜索是关系型数据库无法提供的功能。关系型数据库只能用于处理具有预定义结构、可直接比较值的表格型数据。因此,关系数据库索引也是基于这一点来比较数据。但是 Embedding 向量无法通过这种方式直接相互比较。因为我们不知道向量中的每个值代表什么意思,…...

EtherCAT主站SOEM -- 4 -- SOEM之ethercatprint.h/c文件解析
EtherCAT主站SOEM -- 4 -- SOEM之ethercatprint.h/c文件解析 一 ethercatprint.h/c文件功能预览:二 ethercatprint.h/c 文件的主要函数的作用:2.1.1 char* ec_sdoerror2string(uint32 sdoerrorcode)2.1.2 char* ec_ALstatuscode2string(uint16 ALstatusc…...
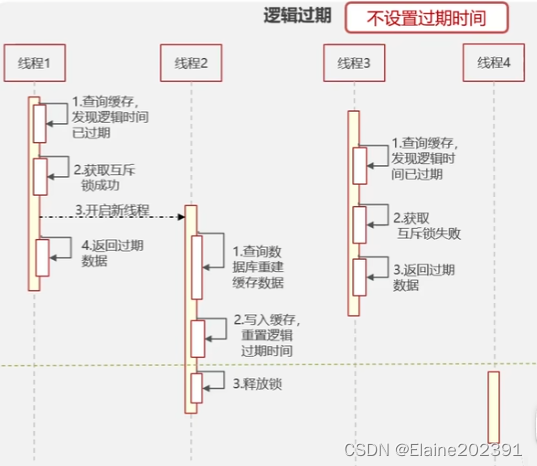
Redis01-缓存击穿、穿透和雪崩
目录 开场白-追命3连 使用场景 01缓存穿透场景与方案 02布隆过滤器 03缓存击穿场景与方案 04缓存雪崩场景与方案 开场白-追命3连 看你项目中有说用到Redis,都是哪些场景使用了Redis呢? 如果发生了缓存穿透、击穿、雪崩如何应对呢?缓存…...
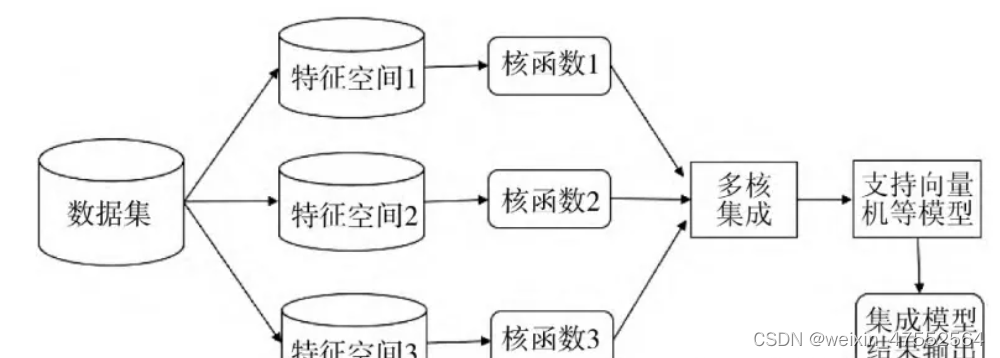
multiple kernel learning(MKL)多核学习
历史上之所以会出现多核学习(MKL)这个词,是因为在深度学习流行起来以前,kernel是处理非线性的默认方法,那个年代优化一个非线性函数不容易,每加一层复杂性可能就需要多设计一个优化算法,MKL就是…...

JS匿名函数之函数表达式与立即执行函数
匿名函数是什么?和具名函数有什么区别?让我为大家介绍一下吧! 没有名字的函数,无法直接使用 一.函数表达式 将匿名函数赋值给一个变量,并且通过变量名去调用,我们将这个称为函数表达式 语法: …...

WebGL:基础练习 / 简单学习 / demo / canvas3D
一、前置内容 canvas:理解canvas / 基础使用 / 实用demo-CSDN博客 WebGL:开始学习 / 理解 WebGL / WebGL 需要掌握哪些知识 / 应用领域 / 前端值得学WebGL吗_webgl培训-CSDN博客 二、在线运行HTML 用来运行WebGL代码,粘贴--运行ÿ…...

Python基础入门例程44-NP44 判断列表是否为空(条件语句)
最近的博文: Python基础入门例程43-NP43 判断布尔值(条件语句)-CSDN博客 Python基础入门例程42-NP42 公式计算器(运算符)-CSDN博客 Python基础入门例程41-NP41 二进制位运算(运算符)-CSDN博客…...

【每日一题Day369】LC187重复的DNA序列 | 字符串哈希
重复的DNA序列【LC187】 DNA序列 由一系列核苷酸组成,缩写为 A, C, G 和 T.。 例如,"ACGAATTCCG" 是一个 DNA序列 。 在研究 DNA 时,识别 DNA 中的重复序列非常有用。 给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA…...

服务器密码机主要功能及特点 安当加密
服务器密码机的主要功能包括: 数据加密:密码机使用各种加密算法对数据进行加密,确保只有拥有正确密钥的接收者才能解密和查看数据。数据解密:密码机使用相应的解密算法和密钥对已加密的数据进行解密,使其恢复成原始数据…...
RIP路由配置
RIP路由配置步骤与命令: 1.启用RIP路由:router rip 2.通告直连网络:network 直连网络 3.启用RIPv2版本:version 2 4.禁用自动汇总:no auto-summary 注意:静态路由通告远程网络,动态路由通告…...
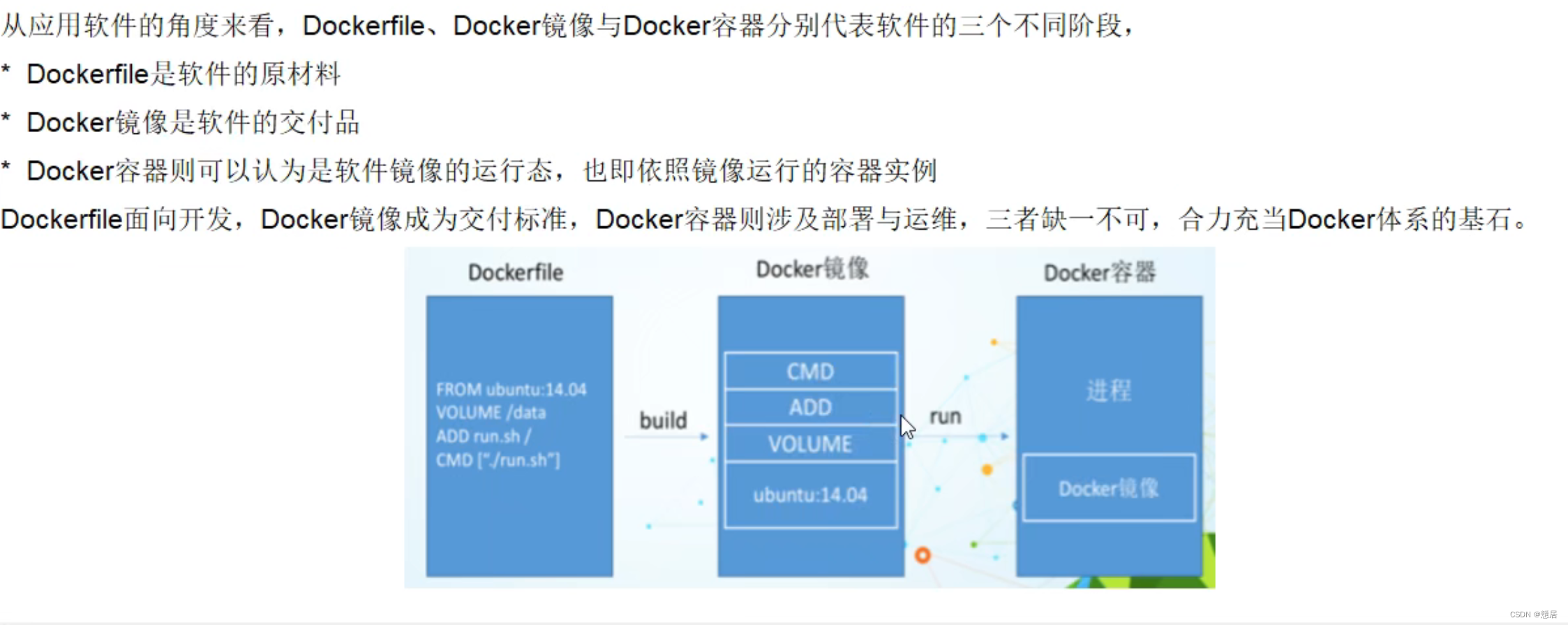
尚硅谷Docker基础篇和Dockerfile超详细整合笔记
Docker基础篇DockerFile Docker:您要如何确保应用能够在这些环境中运行和通过质量检测?并且在部署过程中不出现令人头疼的版本、配置问题,也无需重新编写代码和进行故障修复?而这个就是使用容器。Docker解决了运行环境和配置问题…...
JavaScript_Date对象_实例方法_get类
计算这一年还剩多少天: <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <title>Document&…...

Go语言在区块链开发中的应用
引言 区块链是近年来备受关注的技术领域,它不仅改变了传统的数据交换和存储方式,还为各种应用场景提供了全新的解决方案。而Go语言(Golang)作为一门简洁、高效的编程语言,正逐渐成为开发区块链应用的首选语言。本文将…...

S4.2.4.5 Fast Training Sequence (FTS)
一 本章节主讲知识点 1.1 FTS的用途和实现注意 二 本章节原文翻译 Fast Training Sequence (FTS) 主要用于在L0s->L0跳转的过程中,让Receiver 检测到电气空闲退出,以及实现bit 和 symbol lock。 2.1 Gen1 and Gen2 速率 对于Gen1/2 FTS的组成如下…...

Gitlab CICD实用技巧汇总
关于.gitlab-ci.yml的实用配置 1、stage参数 stages: - build - test - deploy 相同stage的作业会并行执行,有一个失败,则认为这个stage失败。 不同stage的作业会按序执行,前面stage有失败,后续stage不会继续执行。 可以使用ne…...
JavaSpringbootMySQL高校实训管理平台01557-计算机毕业设计项目选题推荐(附源码)
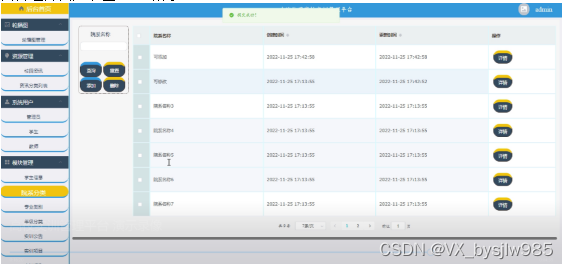
目 录 摘要 1 绪论 1.1 研究背景 1.2 研究意义 1.3论文结构与章节安排 2 高校实训管理平台系统分析 2.1 可行性分析 2.2 系统流程分析 2.2.1 数据增加流程 2.2.2 数据修改流程 2.2.3 数据删除流程 2.3 系统功能分析 2.3.1 功能性分析 2.3.2 非功能性分析 2.4 系…...

初阶JavaEE(14)表白墙程序
接上次博客:初阶JavaEE(13)(安装、配置:Smart Tomcat;访问出错怎么办?Servlet初识、调试、运行;HttpServlet:HttpServlet;HttpServletResponse)-C…...
算法设计与分析第二章作业
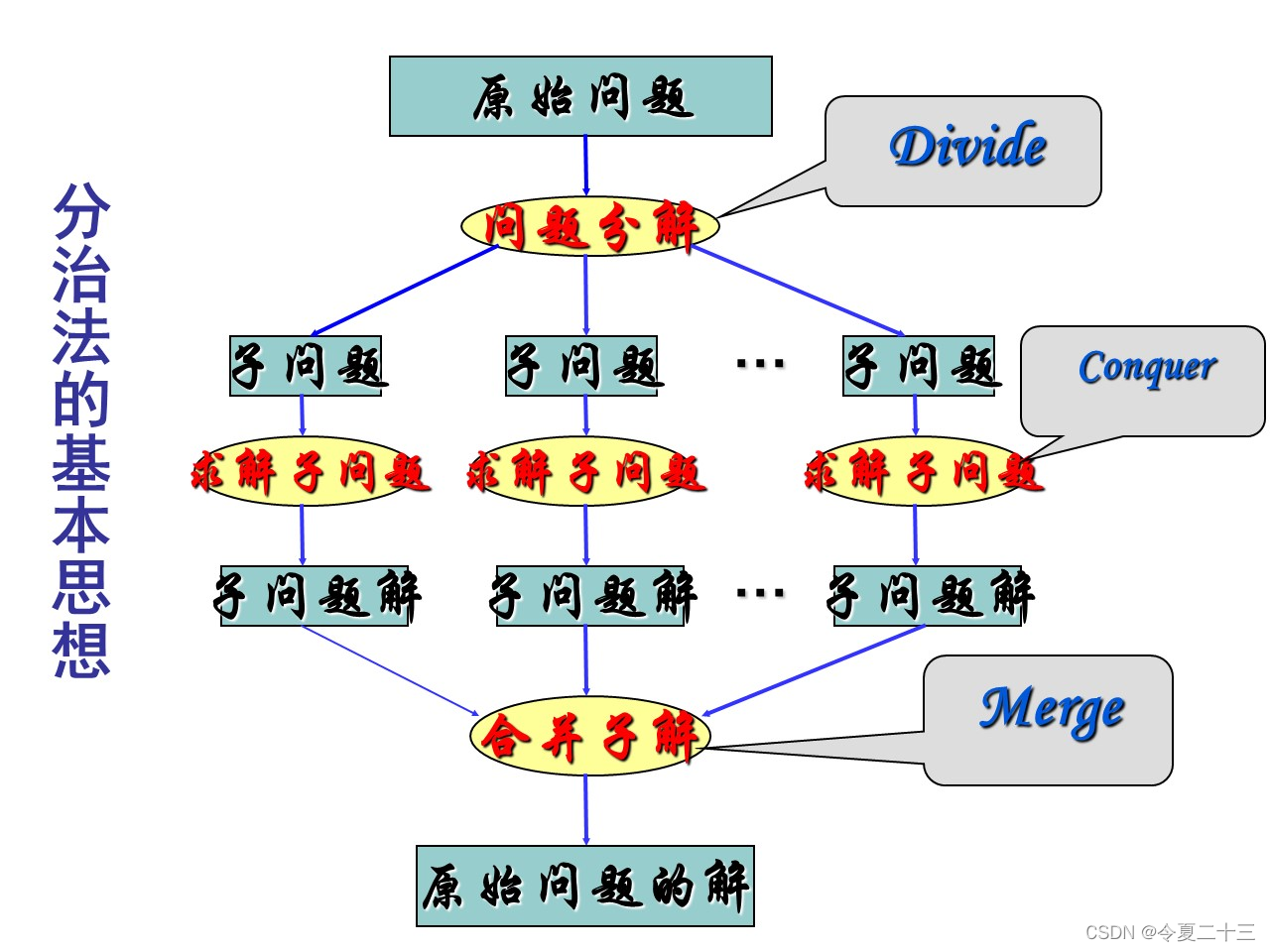
1. 描述最大字段和的分治算法 题目 思路 判断最大子段和,可以用分治的思想,每次将序列一分为二,选择两个序列的最大子段和。 但是这里还有一种可能,就是子段可以横跨两个子序列,所以我们的最大子段和就是࿱…...

《视觉SLAM十四讲》-- 三维空间的刚体运动
文章目录 02 三维空间的刚体运动2.0 机器人位姿表述2.1 点和坐标系2.1.1 三维坐标系有关表述2.1.2 坐标系变换 2.2 旋转向量和欧拉角2.2.1 旋转向量2.2.2 欧拉角 2.3 四元数2.3.1 四元数的定义2.3.2 四元数的计算2.3.3 四元数表示旋转2.3.4 四元数与其他旋转表示法的转换 2.4 相…...

关于iOS:如何使用SwiftUI调整图片大小?
How to resize Image with SwiftUI? 我在Assets.xcassets中拥有很大的形象。 如何使用SwiftUI调整图像大小以缩小图像? 我试图设置框架,但不起作用: 1 2 Image(room.thumbnailImage) .frame(width: 32.0, height: 32.0) 在Image上应用…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
