进口跨境商城源码:高效、安全、可扩展的电商平台解决方案
电子商务的兴起为跨境贸易提供了前所未有的机会和挑战。在这个全球化的时代,跨境电商平台成为许多企业进军国际市场的首选。然而,搭建一个高效、安全、可扩展的进口跨境商城并非易事。
1. 解决方案概述
我们推出的 "进口跨境商城源码" 提供了一个完整的电商平台解决方案,以应对跨境贸易的挑战。我们的源码融合了技术革新和行业经验,旨在帮助企业快速搭建自己的进口跨境商城。
2. 高效的商城架构
我们的商城源码采用先进的软件架构,具备高效的性能和极低的响应时间。通过优化代码和数据库访问,我们确保用户能够获得快速、流畅的购物体验。同时,我们还提供丰富的功能模块和定制化选项,以满足不同企业的需求。
3. 安全保障
在跨境电商平台上,安全性是至关重要的。我们的商城源码内置了多层次的安全机制,包括SSL加密、防火墙和安全认证等。我们还提供漏洞扫描和安全审计服务,以确保用户的交易和个人信息得到最高级别的保护。
4. 可扩展性和灵活性
随着电商行业的发展和企业的业务需求变化,一个可扩展的平台至关重要。我们的商城源码具备出色的可扩展性,可以轻松集成第三方系统和服务。此外,我们提供定制化开发和升级支持,以满足企业在不同阶段的需求。
5. 实用性和可维护性
我们的商城源码注重实用性和可维护性。我们提供详尽的文档和技术支持,以帮助企业轻松上手和运营商城。我们的代码经过优化,易于理解和维护,为企业节省了开发和维护成本。
总之,我们的 "进口跨境商城源码" 是一个高效、安全、可扩展的电商解决方案,为企业构建起一个稳定、可信赖的跨境电商平台提供了有力支持。无论是中小型企业还是大型企业,我们的源码都能满足不同规模和需求的企业,助力其跨国贸易的成功。
相关文章:

进口跨境商城源码:高效、安全、可扩展的电商平台解决方案
电子商务的兴起为跨境贸易提供了前所未有的机会和挑战。在这个全球化的时代,跨境电商平台成为许多企业进军国际市场的首选。然而,搭建一个高效、安全、可扩展的进口跨境商城并非易事。 1. 解决方案概述 我们推出的 "进口跨境商城源码" 提供了一…...
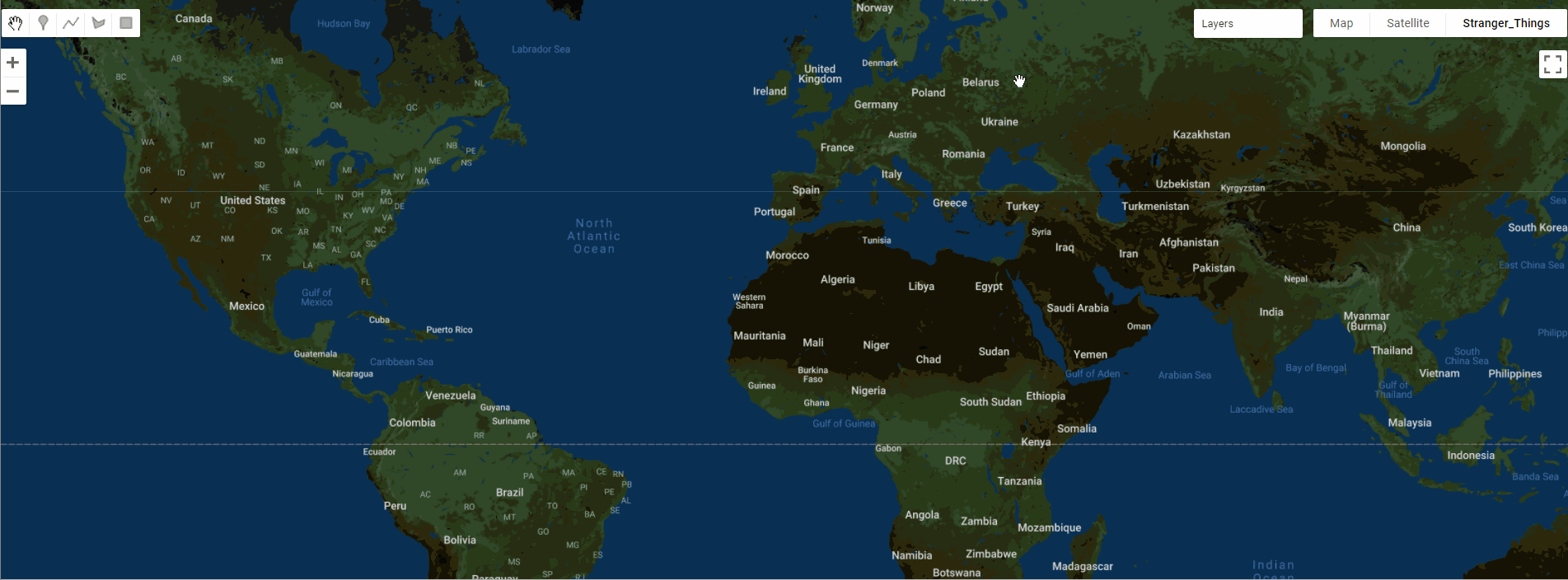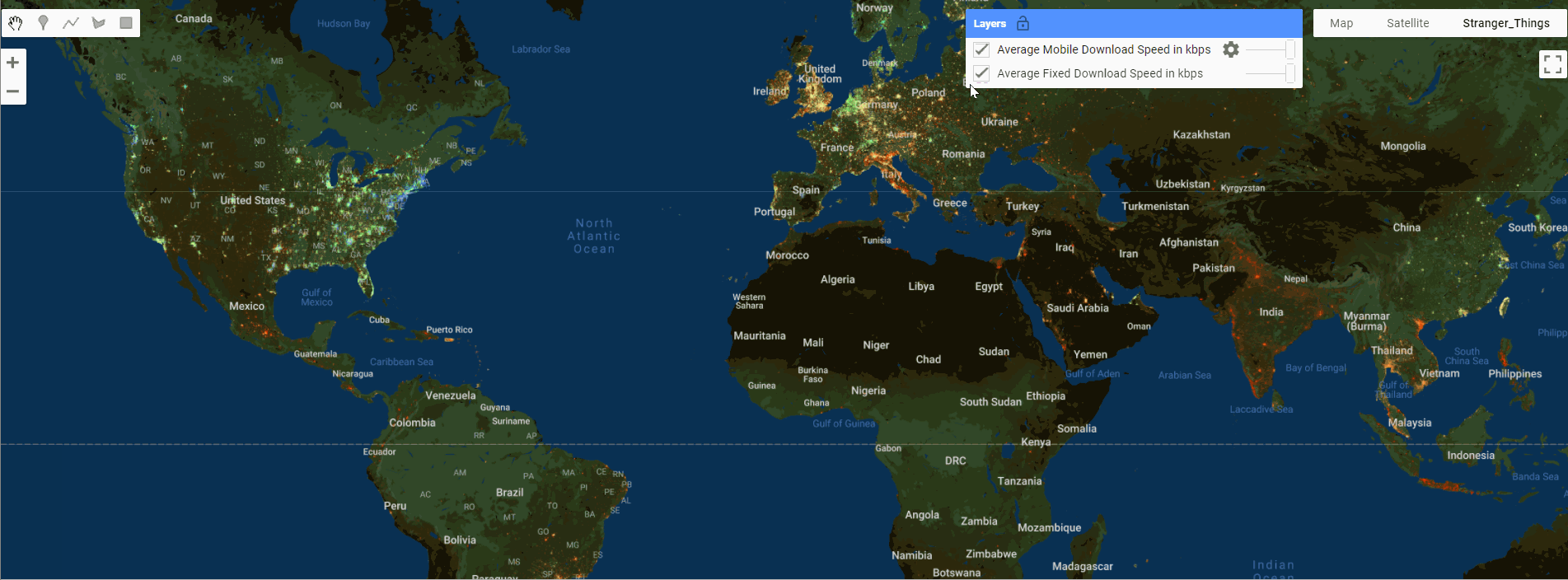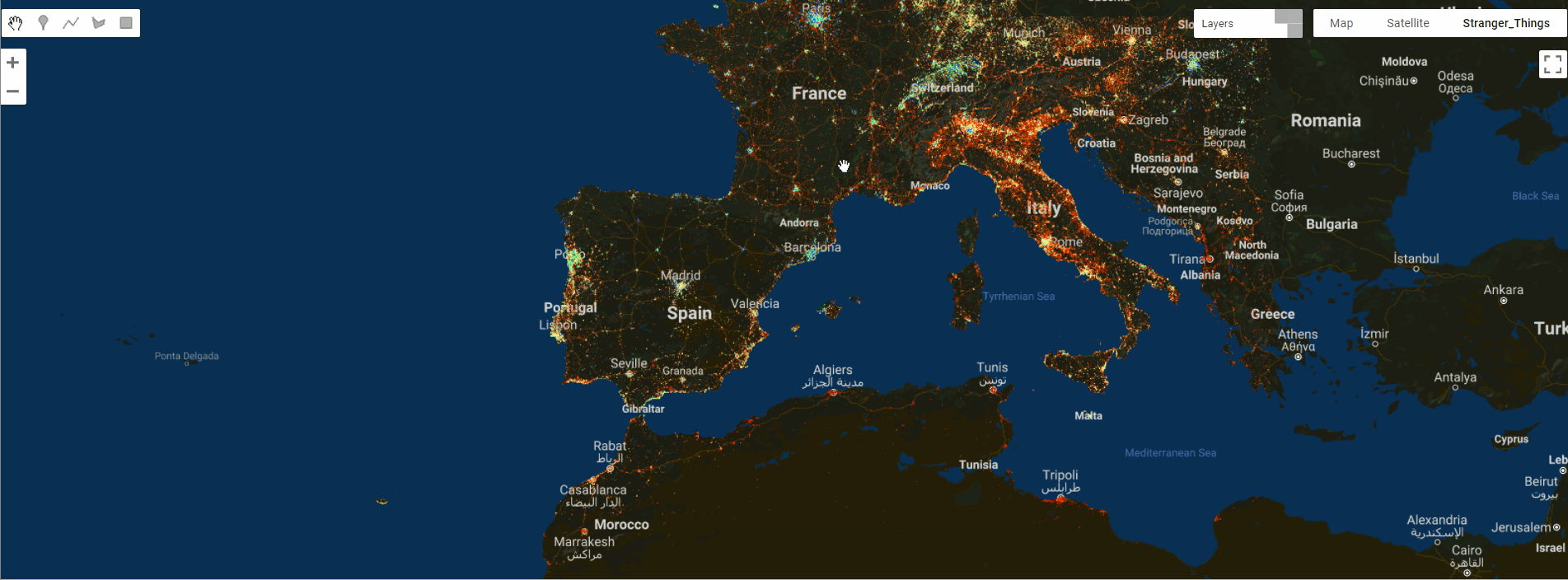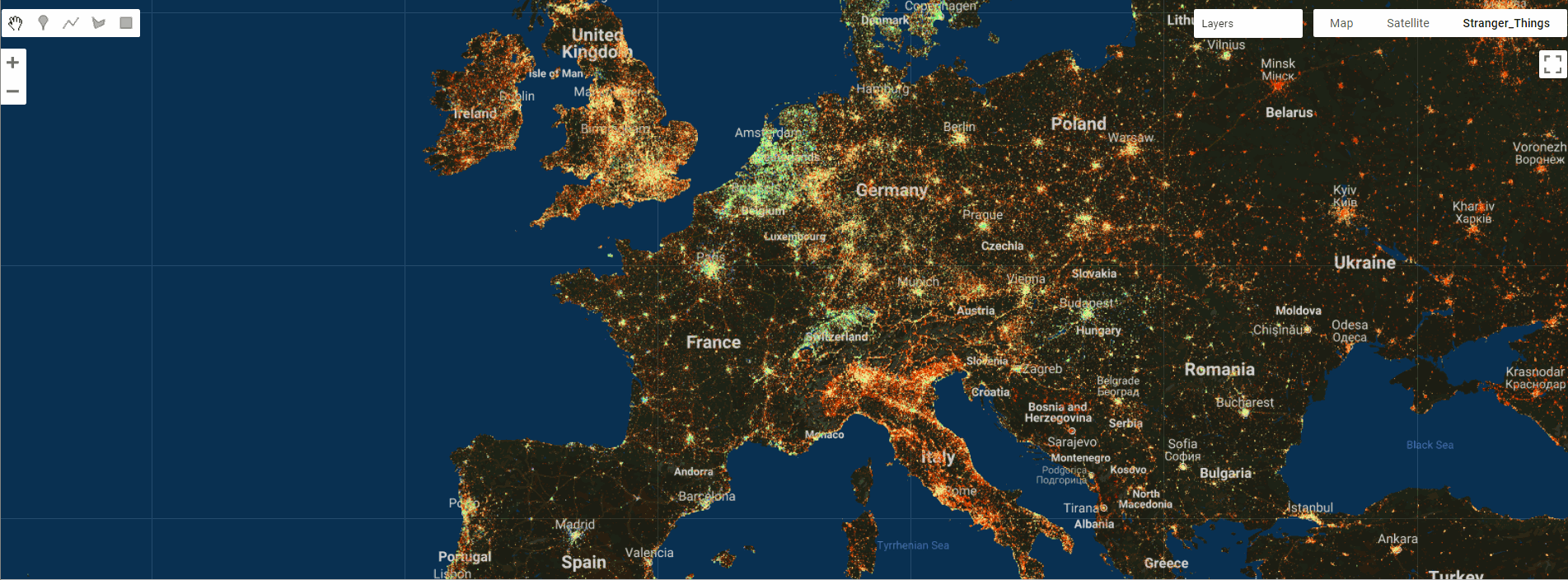
GEE数据集——2019、2020、2021、2022和2023年全球固定宽带和移动(蜂窝)网络性能Shapefile 格式数据集
全球固定宽带和移动(蜂窝)网络性能 全球固定宽带和移动(蜂窝)网络性能,分配给缩放级别 16 网络墨卡托图块(赤道处约 610.8 米 x 610.8 米)。数据以 Shapefile 格式和 Apache Parquet 格式提供&…...
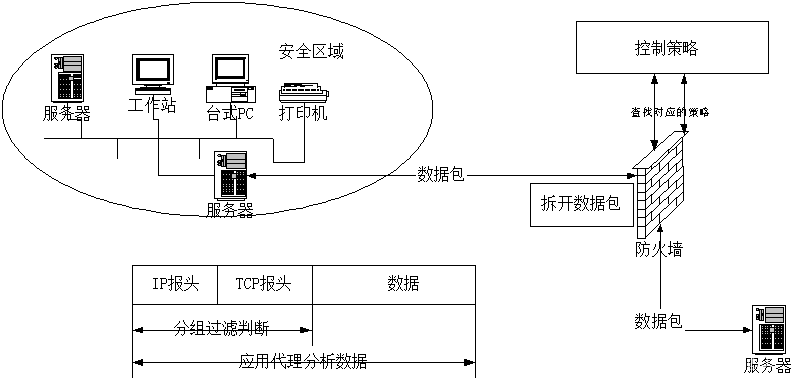
什么是防火墙?详解三种常见的防火墙及各自的优缺点
目录 防火墙的定义 防火墙的功能 防火墙的特性 防火墙的必要性 防火墙的优点 防火墙的局限性 防火墙的分类 分组过滤防火墙 优点: 缺点: 应用代理防火墙 优点 缺点 状态检测防火墙 优点 缺点 防火墙的定义 防火墙的本义原是指古代人们…...

动态规划算法实现0-1背包问题Java语言实现
问题介绍: 动态规划算法: 动态规划(Dynamic Programming)是一种解决多阶段决策问题的优化算法。它通过将问题分解为一系列子问题,并利用子问题的解来构建更大规模问题的解,从而实现对整个问题的求解。 动态…...

linux查看系统版本
linux主机 hostnamectl -- 可以查看 “系统架构”,“发行版本”和“内核版本”等信息 uname -a -- 查看内核版本 cat /proc/version -- 查看当前操作系统版本信息 cat /etc/issue ,lsb_release -a(ubuntu)-- 查看…...
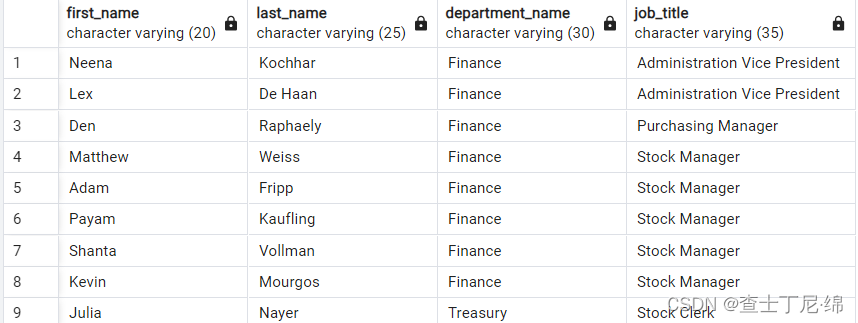
pg14-sql基础(四)-多表联查
多表联查 内联查询 SELECT e.department_id, e.first_name, d.department_name FROM employees e INNER JOIN departments d -- JOIN departments d ON e.department_id d.department_id;左外联查询 SELECT e.department_id, e.first_name, d.department_name FROM employees…...

el-date-picker 日期时间选择器 限时时间范围 精确到时分秒
官方的disabledDate属性:设置禁用状态,参数为当前日期,要求返回 Boolean,它只能禁用日期,对于时间并不能直接禁用,总结以下两个方法解决禁用时间: 1.通过watch去监听源数据: 1.1 组…...
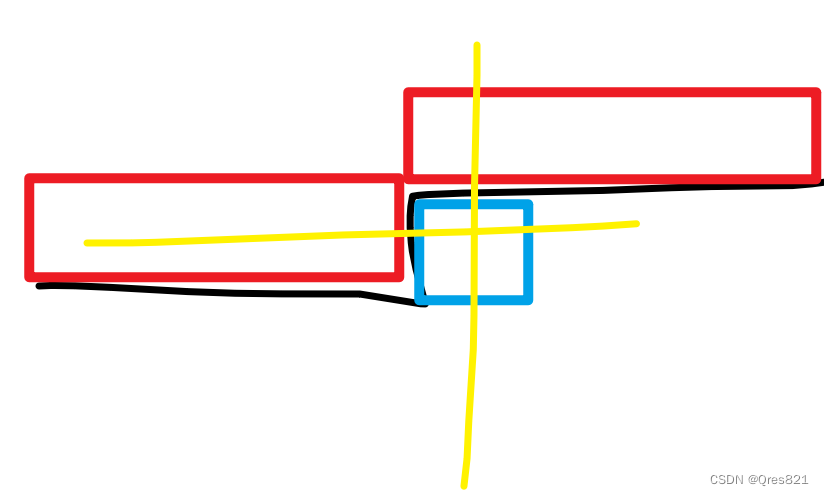
轮廓线dp:GYM103446C
https://vjudge.net/contest/591700#problem/H 考虑轮廓线dp,当我们枚举到蓝色格子的时候,我们记录红色格子的状态 每个格子有4种状态 0有向下1需要向上2不用管3需向右 每次枚举的时候,我们需要考虑这个格子的三种状态: 10不放…...

羊驼免疫制备纳米抗体
纳米抗体(nanobodies,Nbs)是由比利时科学家Hamers等人在骆驼血液内首次发现的一种新型抗体,与传统抗体相比,这种抗体不存在轻链,只有重链抗体(HcAb)和两个常规的CH2和CH3区组成&…...

【AI好好玩02】利用Lama Cleaner本地实现AIGC试玩:擦除对象、替换对象、更换风格等等
目录 一、安装二、擦除功能1. LaMa模型实操实例一:去除路人实操实例二:去水印实操实例三:老照片修复 2. LDM模型3. ZITS模型4. MAT模型5. FcF模型6. Manga模型 三、替换对象功能1. sd1.52. sd23. anything44. realisticVision1.45. 四个模型的…...
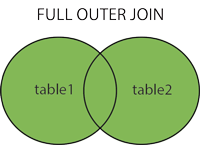
SQL FULL OUTER JOIN 关键字(完整外部连接)||SQL自连接 Self JOIN
SQL FULL OUTER JOIN 关键字 当左(表1)或右(表2)表记录匹配时,FULL OUTER JOIN关键字将返回所有记录。 注意: FULL OUTER JOIN可能会返回非常大的结果集! SQL FULL OUTER JOIN 语法 SELECT …...

专科医院污水处理设备构造解析及工艺流程
诸城市鑫淼环保小编带大家了解一下专科医院污水处理设备构造解析及工艺流程 主要组成部分: 1.预处理单元 处理流程的起点是预处理单元,用于去除废水中的大颗粒物质和固体废物。这一阶段通常包括隔栅和筛网,以确保进一步处理的污水清洁。 2.生…...

【RabbitMQ】RabbitMQ 消息的可靠性 —— 生产者和消费者消息的确认,消息的持久化以及消费失败的重试机制
文章目录 前言:消息的可靠性问题一、生产者消息的确认1.1 生产者确认机制1.2 实现生产者消息的确认1.3 验证生产者消息的确认 二、消息的持久化2.1 演示消息的丢失2.2 声明持久化的交换机和队列2.3 发送持久化的消息 三、消费者消息的确认3.1 配置消费者消息确认3.2…...

百万套行泊一体量产定点,中国市场「开启」智驾高低速集成
进入2023年,席卷中国市场的行泊一体概念方案进入定点、量产交付的第一波高峰期。这套方案,以高性价比、硬件复用、高低速智驾集成的模式,备受市场青睐。 本周,纵目科技宣布,Amphiman3000行泊一体产品获得长安汽车旗下…...
Gopro hero5运动相机格式化后恢复案例
Gopro运动相机以稳定著称,旗下的Hero系列销售全球。下面我们来看一个Hero5格式化后拍了少量素材的恢复案例。 故障存储:64G MicroSD卡 Exfat文件系统 故障现象: 64G的卡没备份数据时做了格式化操作又拍了一条,发现数据没有备份,客户自行使…...

Microsoft Dynamics 365 CE 扩展定制 - 6. 增强代码
在本章中,我们将介绍以下内容: 使用三层模式重构插件用QueryExpressions替换LINQ数据访问层记录自定义项中的错误将插件转换为自定义工作流活动单元测试插件业务逻辑使用内存上下文对插件进行单元测试端到端集成测试插件分析插件构建通用读取审核插件利用CRM Online实现跨来源…...

基于libopenh264 codec的svc分层流实现方案
OpenH264 http://www.openh264.org/ 是标准的H.264 encoder/decoder. ffmpeg已经集成libopenh264,但不支持svc特性。 openh264 encoder支持svc特性: 1. 时域4层:Temporal scalability up to 4 layers in a dyadic hierarchy 2. 空域4层&#…...

为机器学习算法准备数据(Machine Learning 研习之八)
本文还是同样建立在前两篇的基础之上的! 属性组合实验 希望前面的部分能让您了解探索数据并获得洞察力的几种方法。您发现了一些数据怪癖,您可能希望在将数据提供给机器学习算法之前对其进行清理,并且发现了属性之间有趣的相关性,…...

基于Python OpenCV的金铲铲自动进游戏、D牌...
基于Python OpenCV的金铲铲自动进游戏、D牌... 1. 自动点击进入游戏1.1 环境准备1.2 功能实现2. 自动D牌3. 游戏结束自动退1. 自动点击进入游戏 PS: 本测试只用于交流学习OpenCV的相关知识,不能用于商业用途,后果自负。 1.1 环境准备 需要金铲铲在win10的模拟器,我们这里选…...

c++中httplib使用
httplib文件链接:百度网盘 请输入提取码 提取码:kgnq json解析库:百度网盘 请输入提取码 提取码:oug0 一、获取token 打开postman, 在body这个参数中点击raw,输入用户名和密码 然后需要获取到域名和地址。 c++代码如下: #include "httplib.h" #in…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
