可达矩阵-邻接矩阵-以及有向图的python绘制
参考1
自定义输入矩阵来绘制
根据参考代码,
自定义
代码如下:
# 编程实现有向图连通性的判断
from pylab import mplmpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
import pylab#定义x三阶矩阵
x = np.array([[1, 0, 0], [1, 1, 0], [1, 1, 1]])#随机生成x为五阶矩阵
# x = np.random.randint(0, 2, (5, 5))
n = len(x)value_1 = value_2 = sum_1 = sum_2 = sum_3 = sum_4 = y = final = x
y = x + x.T# 计算可达矩阵
for i in range(1, n):value_1 = np.matmul(value_1, x)sum_1 = sum_1 + value_1
sum_2 = sum_1 + np.identity(n)reachability_matrix = sum_2 > 0.5print("此有向图的可达矩阵为:")
print(reachability_matrix.astype(int))final = reachability_matrix + reachability_matrix.Tfor i in range(1, n):value_2 = np.matmul(value_2, y)sum_3 = sum_3 + value_2
sum_4 = sum_3 + np.identity(n)
reachability_matrix_1 = sum_4 > 0.5# 给出判断结果
if ((reachability_matrix.astype(int) == np.ones((n, n)).astype(int)).all()):print("此有向线图G为强连通图或其为无向连通图")
elif ((final.astype(int) == np.ones((n, n)).astype(int)).all()):print("此有向线图G是单向连通图")
elif ((reachability_matrix_1.astype(int) == np.ones((n, n)).astype(int)).all()):print("此有向线图G是弱连通图")
else:print("此有向图不连通")# 下面展示图形化输出有向图G
G = nx.DiGraph()
for i in range(0, n):j=i+1G.add_node(i, desc='p' + str(j))for p in range(0, n):for q in range(0, n):if x[p, q] == 1:G.add_edges_from([(p, q)], weight='1')edge_labels = dict([((u, v), d['weight']) for u, v, d in G.edges(data=True)])
edge_colors = ['black']
pos = nx.spring_layout(G)
node_labels = nx.get_node_attributes(G, 'desc')
nx.draw_networkx_labels(G, pos, labels=node_labels)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
nx.draw(G, pos, node_size=1500, edge_color=edge_colors, edge_cmap=plt.cm.Reds)
plt.title('Directed Graph', fontsize=10)
pylab.show()第二版
增大了字体
可以自定义字体大小
# 编程实现有向图连通性的判断
from pylab import mplmpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
import pylab#定义x三阶矩阵
x = np.array([[1, 0, 0], [1, 1, 0], [1, 1, 1]])#随机生成x为五阶矩阵
# x = np.random.randint(0, 2, (5, 5))
n = len(x)value_1 = value_2 = sum_1 = sum_2 = sum_3 = sum_4 = y = final = x
y = x + x.T# 计算可达矩阵
for i in range(1, n):value_1 = np.matmul(value_1, x)sum_1 = sum_1 + value_1
sum_2 = sum_1 + np.identity(n)reachability_matrix = sum_2 > 0.5print("此有向图的可达矩阵为:")
print(reachability_matrix.astype(int))final = reachability_matrix + reachability_matrix.Tfor i in range(1, n):value_2 = np.matmul(value_2, y)sum_3 = sum_3 + value_2
sum_4 = sum_3 + np.identity(n)
reachability_matrix_1 = sum_4 > 0.5# 给出判断结果
if ((reachability_matrix.astype(int) == np.ones((n, n)).astype(int)).all()):print("此有向线图G为强连通图或其为无向连通图")
elif ((final.astype(int) == np.ones((n, n)).astype(int)).all()):print("此有向线图G是单向连通图")
elif ((reachability_matrix_1.astype(int) == np.ones((n, n)).astype(int)).all()):print("此有向线图G是弱连通图")
else:print("此有向图不连通")# 下面展示图形化输出有向图G
G = nx.DiGraph()
for i in range(0, n):j = i + 1G.add_node(i, desc='p' + str(j))for p in range(0, n):for q in range(0, n):if x[p, q] == 1:G.add_edges_from([(p, q)], weight='1')edge_labels = dict([((u, v), d['weight']) for u, v, d in G.edges(data=True)])
edge_colors = ['black']
pos = nx.spring_layout(G)
node_labels = nx.get_node_attributes(G, 'desc')
nx.draw_networkx_labels(G, pos, labels=node_labels, font_size=16) # 设置字体大小为16nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=12)nx.draw(G, pos, node_size=1500, edge_color=edge_colors, edge_cmap=plt.cm.Reds)
plt.title('Directed Graph', fontsize=10)
pylab.show()
相关文章:

可达矩阵-邻接矩阵-以及有向图的python绘制
参考1 自定义输入矩阵来绘制 根据参考代码, 自定义 代码如下: # 编程实现有向图连通性的判断 from pylab import mplmpl.rcParams[font.sans-serif] [SimHei] mpl.rcParams[axes.unicode_minus] False import numpy as np import networkx as nx imp…...

react typescript @别名的使用
1、config/webpack.config.js中找到alias,添加: path.resolve(src) ,如下: alias: {// Support React Native Web// https://www.smashingmagazine.com/2016/08/a-glimpse-into-the-future-with-react-native-for-web/"react-native&qu…...

C++性能优化笔记-6-C++元素的效率差异-7-类型转换
C元素的效率差异 类型转换signed与unsigned转换整数大小转换浮点精度转换整数到浮点转换浮点到整数转换指针类型转换重新解释对象的类型const_caststatic_castreinterpret_castdynamic_cast转换类对象 类型转换 在C语法中,有几种方式进行类型转换: // …...

c#中switch常用模式
声明模式 首先检查value的类型,然后根据类型输出相应的消息 public void ShowMessage(object value) {switch (value){case int i: Console.WriteLine($"value is int:{i}"); break;case long l: Console.WriteLine($"value is long:{l}"); b…...

Flink SQL 常用作业sql
目录 flink sql常用配置kafka source to mysql sink窗口函数 开窗datagen 自动生成数据表tumble 滚动窗口hop 滑动窗口cumulate 累积窗口 grouping sets 多维分析over 函数TopN flink sql常用配置 设置输出结果格式 SET sql-client.execution.result-modetableau;kafka source…...
nodejs国内镜像及切换版本工具nvm
淘宝 NPM 镜像站(http://npm.taobao.org)已更换域名,新域名: Web 站点:https://npmmirror.com Registry Endpoint:https://registry.npmmirror.com 详见: 【望周知】淘宝 NPM 镜像换域名了&…...

用Rust和Scraper库编写图像爬虫的建议
本文提供一些有关如何使用Rust和Scraper库编写图像爬虫的一般建议: 1、首先,你需要安装Rust和Scraper库。你可以通过Rustup或Cargo来安装Rust,然后使用Cargo来安装Scraper库。 2、然后,你可以使用Scraper库的Crawler类来创建一个…...

Java 语言环境搭建
JDK 是一种用于构建在 Java 平台上发布的应用程序、Applet 和组件的开发环境,即编写 Java 程序必须使用 JDK,它提供了编译和运行 Java 程序的环境。 在安装 JDK 之前,首先要到 Oracle 网站获取 JDK 安装包。JDK 安装包被集成在 Java SE 中&a…...
酷开科技 | 酷开系统里萌萌哒小维在等你!
在一片金黄淡绿的颜色中,深秋的脚步更近了,在这个气候微凉的季节里,你是不是更想拥有一种温暖的陪伴呢?酷开科技智慧AI语音功能更懂你,贴心的小维用心陪伴你的每一天。 01.全天候陪伴 在酷开系统中,只要你…...

Bash 4关联数组:错误“声明:-A:无效选项”
Bash 4 associative arrays: error “declare: -A: invalid option” 就是bash版本太低 1.先确定现在的版本 bash -version 我的就是版本太低 升级新版本bash4.2 即可 升级步骤 1.下载bash-4.2wget http://ftp.gnu.org/gnu/bash/bash-4.2.tar.gz 2. 下载完成解压 tar -zxvf…...

干货|AI辅助完成论文的正确打开方式!
论文写作中可能遇到问题 1. 选题问题:是否无法确定研究方向和选择合适的题目? 2. 文献综述问题:是否困惑如何进行文献调研和综述? 3. 方法论问题:是否不知道该选择何种研究方法? 4. 数据处理问题&#…...
SpringBoot--Web开发篇:含enjoy模板引擎整合,SpringBoot整合springMVC;及上传文件至七牛云;restFul
SpringBoot的Web开发 官网学习: 进入spring官网 --> projects --> SpringBoot --> LEARN --> Reference Doc. --> Web --> 就能看到上述页面 静态资源映射规则 官方文档 总结: 只要是静态资源,放在类路径下࿱…...

线上JAVA应用平稳运行一段时间后出现JVM崩溃问题 | 京东云技术团队
一、问题是怎么发现的 系统是一个定时任务系统,需要定时执行业务代码,业务代码主要是访问MYSQL数据库和缓存进行操作,该开始启动,系统日志一切正常,但是运行一段时间到凌晨后,系统就自动崩溃了,…...
进口跨境商城源码:高效、安全、可扩展的电商平台解决方案
电子商务的兴起为跨境贸易提供了前所未有的机会和挑战。在这个全球化的时代,跨境电商平台成为许多企业进军国际市场的首选。然而,搭建一个高效、安全、可扩展的进口跨境商城并非易事。 1. 解决方案概述 我们推出的 "进口跨境商城源码" 提供了一…...
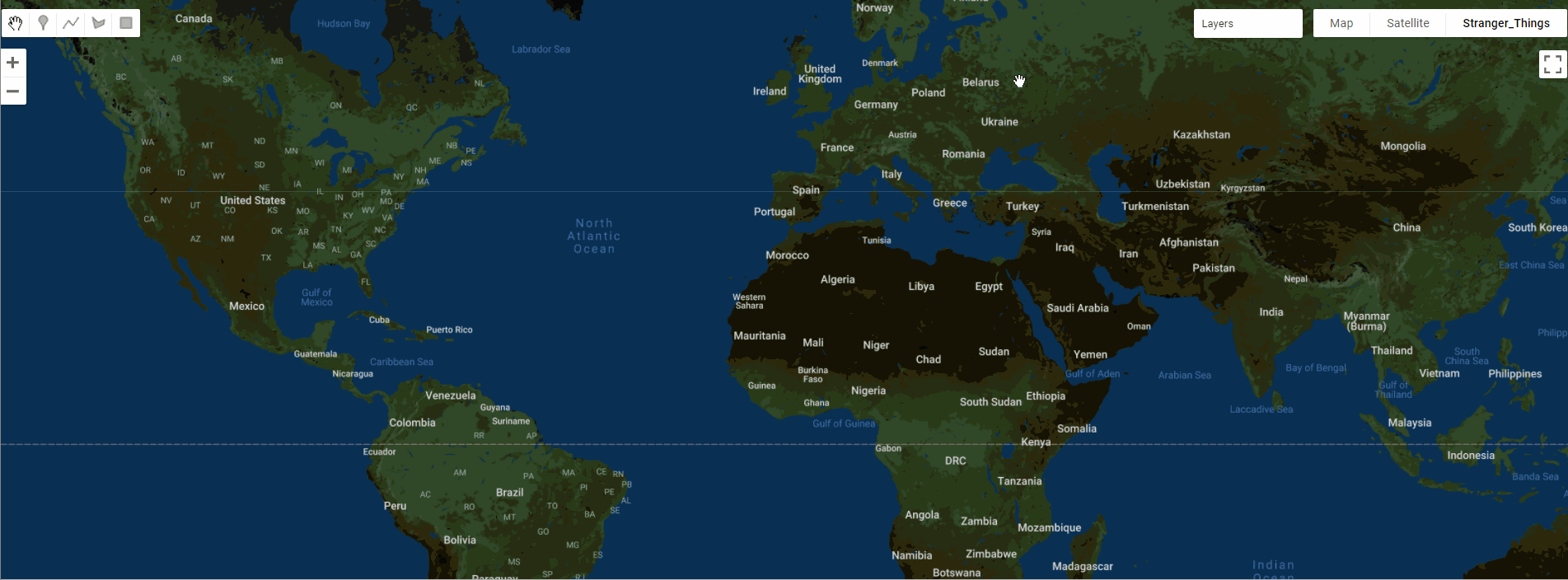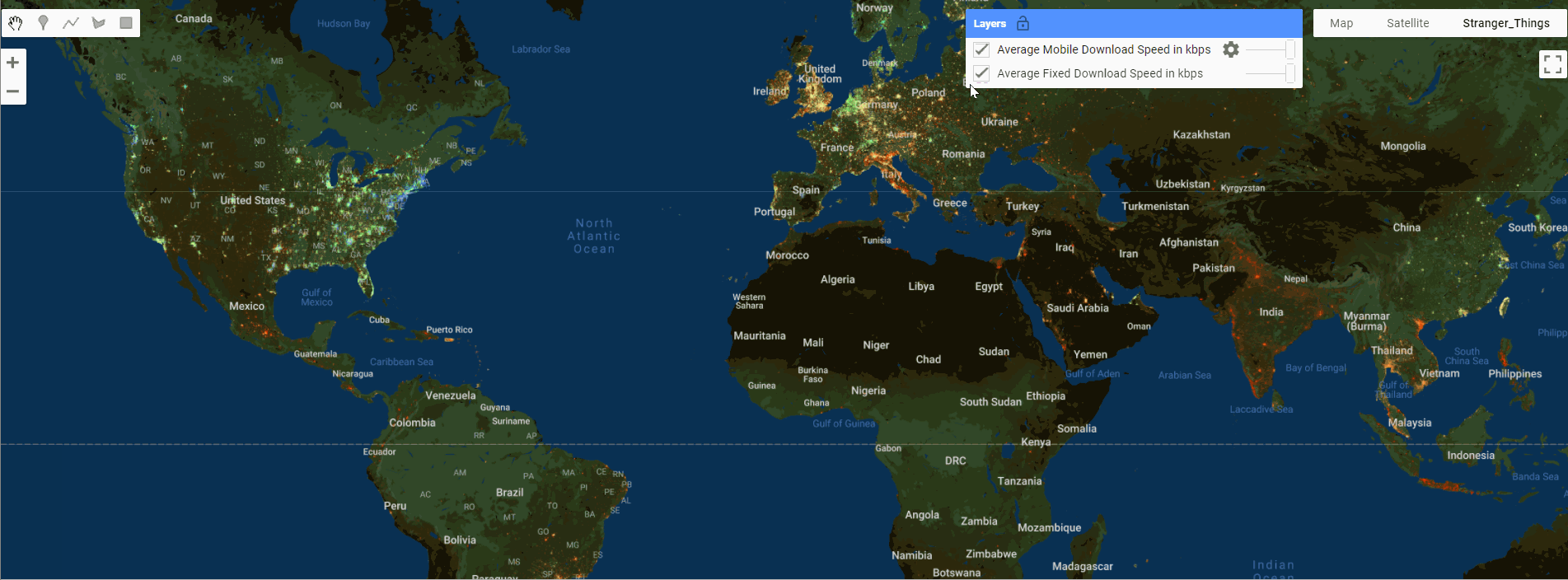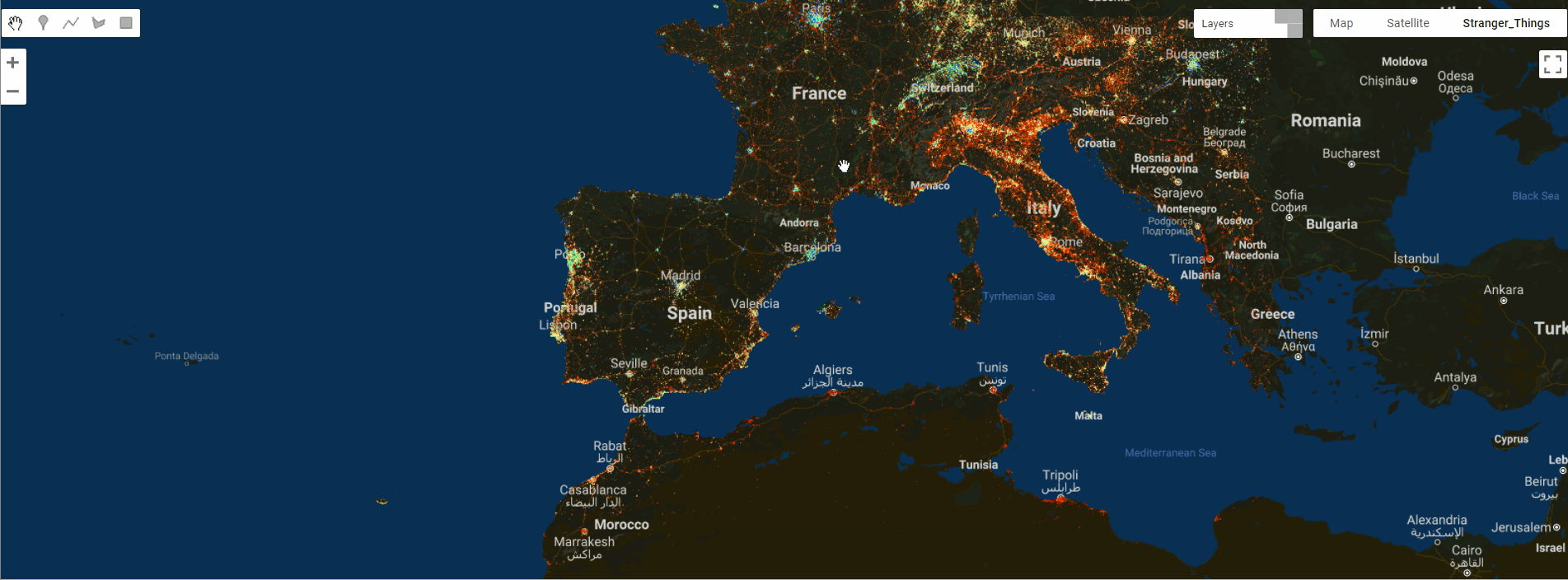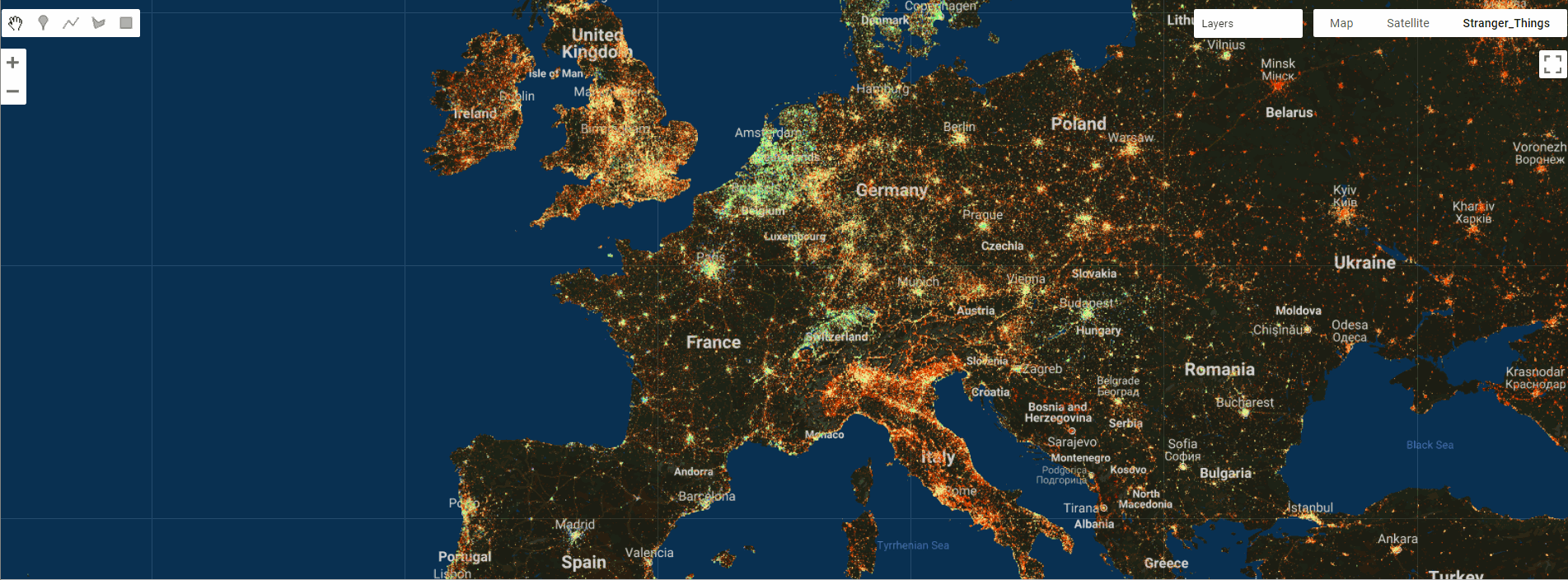
GEE数据集——2019、2020、2021、2022和2023年全球固定宽带和移动(蜂窝)网络性能Shapefile 格式数据集
全球固定宽带和移动(蜂窝)网络性能 全球固定宽带和移动(蜂窝)网络性能,分配给缩放级别 16 网络墨卡托图块(赤道处约 610.8 米 x 610.8 米)。数据以 Shapefile 格式和 Apache Parquet 格式提供&…...
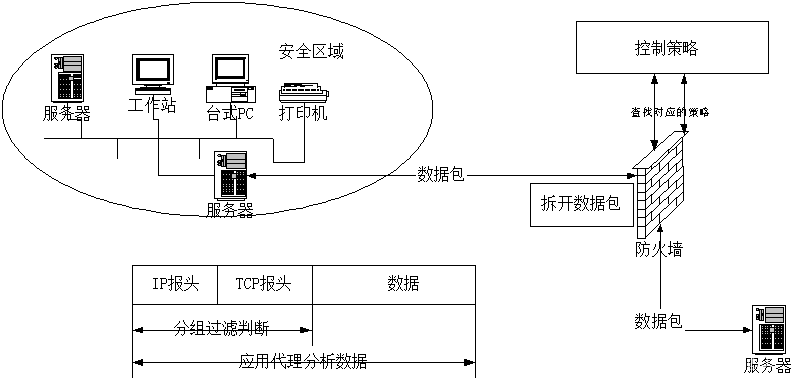
什么是防火墙?详解三种常见的防火墙及各自的优缺点
目录 防火墙的定义 防火墙的功能 防火墙的特性 防火墙的必要性 防火墙的优点 防火墙的局限性 防火墙的分类 分组过滤防火墙 优点: 缺点: 应用代理防火墙 优点 缺点 状态检测防火墙 优点 缺点 防火墙的定义 防火墙的本义原是指古代人们…...

动态规划算法实现0-1背包问题Java语言实现
问题介绍: 动态规划算法: 动态规划(Dynamic Programming)是一种解决多阶段决策问题的优化算法。它通过将问题分解为一系列子问题,并利用子问题的解来构建更大规模问题的解,从而实现对整个问题的求解。 动态…...

linux查看系统版本
linux主机 hostnamectl -- 可以查看 “系统架构”,“发行版本”和“内核版本”等信息 uname -a -- 查看内核版本 cat /proc/version -- 查看当前操作系统版本信息 cat /etc/issue ,lsb_release -a(ubuntu)-- 查看…...
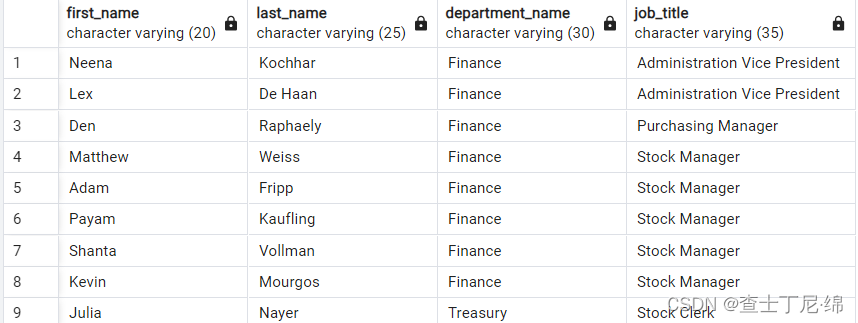
pg14-sql基础(四)-多表联查
多表联查 内联查询 SELECT e.department_id, e.first_name, d.department_name FROM employees e INNER JOIN departments d -- JOIN departments d ON e.department_id d.department_id;左外联查询 SELECT e.department_id, e.first_name, d.department_name FROM employees…...

el-date-picker 日期时间选择器 限时时间范围 精确到时分秒
官方的disabledDate属性:设置禁用状态,参数为当前日期,要求返回 Boolean,它只能禁用日期,对于时间并不能直接禁用,总结以下两个方法解决禁用时间: 1.通过watch去监听源数据: 1.1 组…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
