151、【动态规划】AcWing ——2. 01背包问题:二维数组+一维数组(C++版本)
题目描述
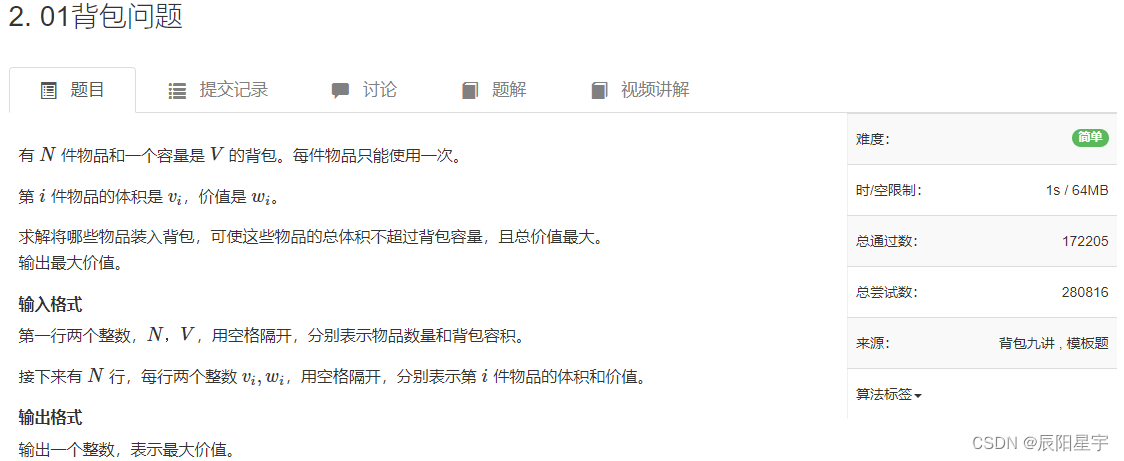
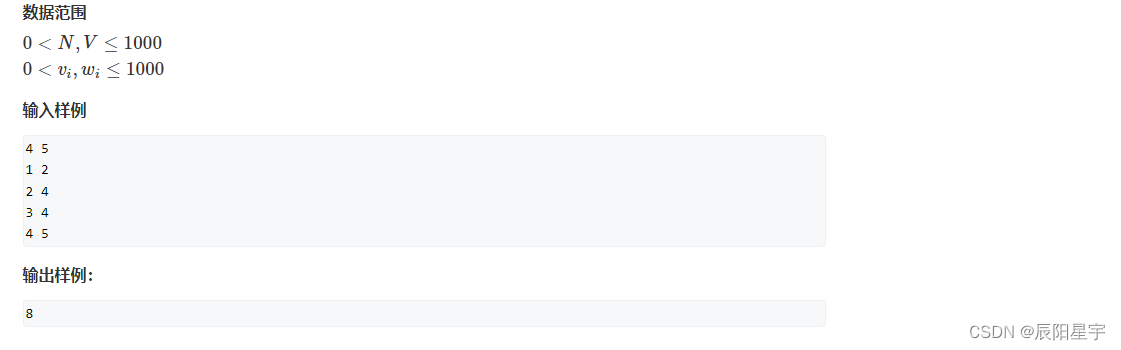
原题链接:2. 01背包问题
解题思路
(1)二维dp数组
动态规划五步曲:
(1)dp[i][j]的含义: 容量为j时,从物品1-物品i中取物品,可达到的最大价值
(2)递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]),其中dp[i - 1][j]表示不放物品i时的最大价值;j - v[i]表示给物品i留出空间,dp[i - 1][j - v[i]]表示给物品i留出空间后,放入其余物品可达到的最大价值(由于是按物品递增顺序遍历,因此为从1-i-1的物品),dp[i - 1][j - v[i]] + w[i]表示放入物品i和其余放入其余物品,可到达的最大价值。
(3)dp数组初始化: dp[0][j] = d[i][0] = 0, dp[0][j]中j >= v[i]的取w[i]
(4)遍历顺序: 从小到大,先背包后物品,或先物品后背包都可以。
(5)举例: 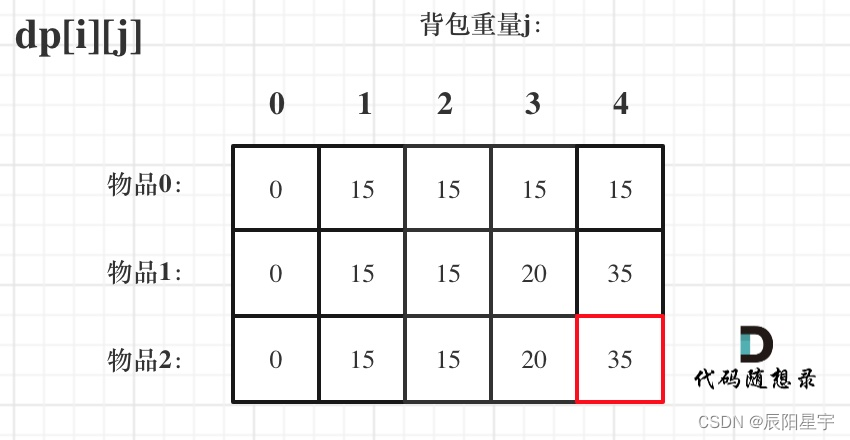
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1010;
int dp[N][N];int main(){int n, m;int v[N], w[N];cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {// 当前物品重量大于背包容量时,不放该物品if(j < v[i]) dp[i][j] = dp[i - 1][j];// 当前物品重量小于等于背包容量时,在放该物品后和不放该物品之间选择一个最大价值else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);}}cout << dp[n][m] << endl;return 0;
}
(2)优化为一维dp数组(滚动数组)
滚动数组含义:本轮所计算的数,需要用到上一轮的结果,依次类推,滚动计算。
优化成一维那就要在遍历上实现与二维相同的逻辑顺序,从而实现仅用一维就可以代替二维。
动态规划五步曲:
(1)dp[j]数组的含义: 容量为j时,装入的物品可达到的最大价值。
(2)递推公式: dp[j] = max(dp[j], dp[j - v[i]])
(3)dp数组初始化: dp[0] = 0
(4)遍历顺序: 两层for循环,先遍历物品,再遍历背包,内层按背包从大到小递减顺序遍历。
如果删除dp中的维度[i]后,还保持对j的从小到大遍历,那么此时的代码其实是等价于dp[i][j] = max(dp[i][j - 1], dp[i][j - v[i]),在一遍后续遍历中,因为j是从小到大与v[i]相减,在后续相减时,可能会出现本轮遍历中用过的数,会使之前使用过的数重复相加。
而如果以对j进行从大到小遍历,因为此时是j是从m到v[i],以此顺序计算dp[j - v[i]]时,在一遍后续遍历中,都是会基于上一轮对i的遍历而进行判定,并且由于j变化而v[i]不变,在后续不会出现使用过的数重复相加。每次遍历到的j所对应dp[j - v[i]]都还没有被更新,就相当于是之前的状态dp[i - 1][j - v[i]],从而得到dp[j] = dp[j - v[i]]就等价于dp[i][j] = dp[i - 1][j - v[i]]。
(5)举例: 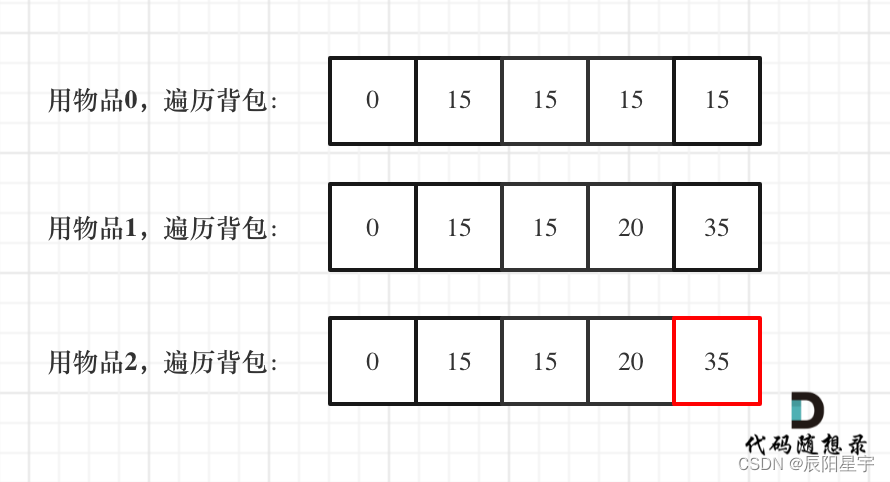
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1010;
int dp[N];int main(){int n, m;int v[N], w[N];cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i++) {// 从后向前遍历,表示装入一个物品后,剩余的可装入容量达到的最大价值for(int j = m; j >= v[i]; j--) {dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}cout << dp[m] << endl;return 0;
}
参考文章:AcWing 2. 01背包问题(状态转移方程讲解) 、AcWing 2. 01背包问题 、动态规划:关于01背包问题,你该了解这些!(滚动数组)
相关文章:

151、【动态规划】AcWing ——2. 01背包问题:二维数组+一维数组(C++版本)
题目描述 原题链接:2. 01背包问题 解题思路 (1)二维dp数组 动态规划五步曲: (1)dp[i][j]的含义: 容量为j时,从物品1-物品i中取物品,可达到的最大价值 (2…...

DS期末复习卷(二)
选择题 1.下面关于线性表的叙述错误的是( D )。 (A) 线性表采用顺序存储必须占用一片连续的存储空间 (B) 线性表采用链式存储不必占用一片连续的存储空间 © 线性表采用链式存储便于插入和删除操作的实现 (D) 线性表采用顺序存储便于插…...
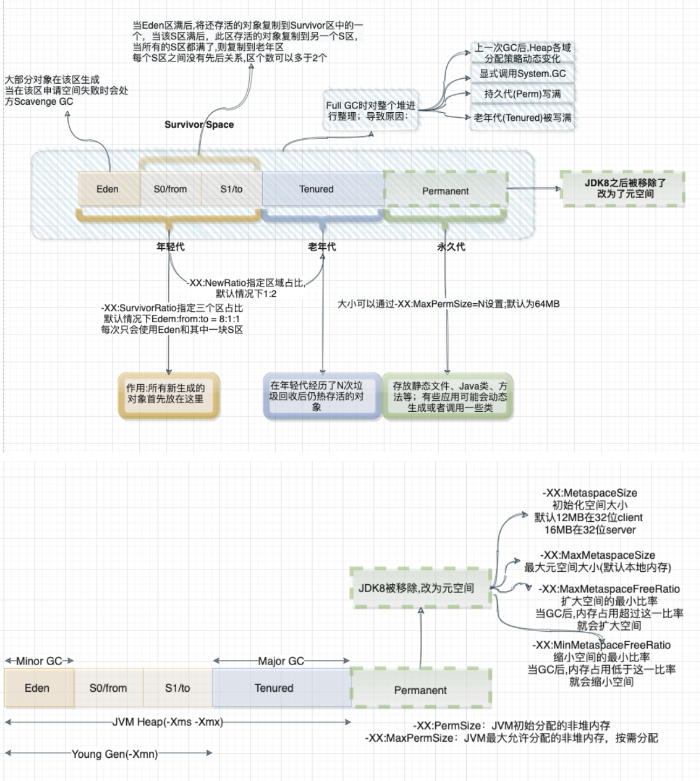
大数据技术架构(组件)31——Spark:Optimize--->JVM On Compute
2.1.9.4、Optimize--->JVM On Compute首要的一个问题就是GC,那么先来了解下其原理:1、内存管理其实就是对象的管理,包括对象的分配和释放,如果显式的释放对象,只要把该对象赋值为null,即该对象变为不可达.GC将负责回…...
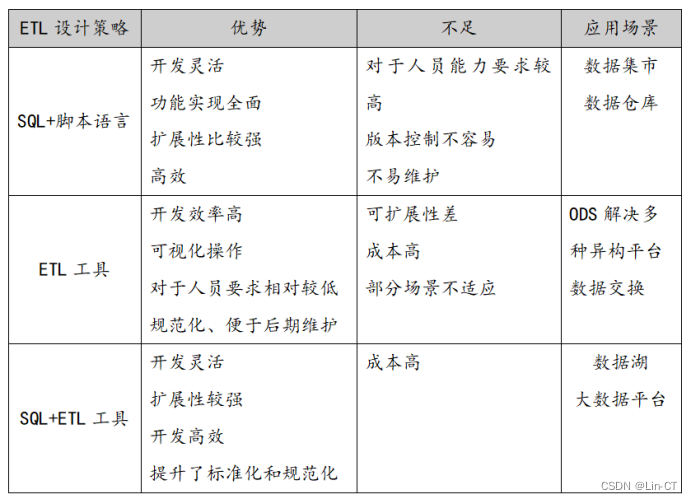
ETL基础概念及要求详解
ETL基础概念及要求详解概念ETL与ELT数据湖与数据仓库ETL应用场景ETL具体流程及操作要求抽取清洗转换加载ETL设计模式SQL脚本语言ETL工具设计ETL工具SQLETL接口设计要求明确接口属性约定接口形式确定接口抽取方法规范接口格式概念 ETL即Extract(抽取)Tra…...

刷题记录:牛客NC23054华华开始学信息学 线段树+分块
传送门:牛客 题目描述: 题目latex公式较多,此处省略 输入: 10 6 1 1 1 2 4 6 1 3 2 2 5 7 1 6 10 2 1 10 输出: 3 5 26这道题让我体验到的线段树相对于树状数组的常数巨大 我们倘若直接用单点修改的话,如果D过小比如1那么我们足足要加n次,时间复杂度爆…...

二叉搜索树(查找,插入,删除)
目录 1.概念 2.性质 3.二叉搜索树的操作 1.查找 2.插入 3.删除(难点) 1.概念 二叉搜索树又称二叉排序树.利用中序遍历它就是一个有顺序的一组数. 2.性质 1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 2.若它的右子树不为空,则右子树上所有节点的值都…...

C# PictureEdit 加载图片
方法一: 如果要加载的图片的长宽比不是太过失衡, 1.可以改变picturebox的SizeMode属性为 PictureBoxSizeMode.StretchImage, 2.或者Dev控件 PictureEdit的SizeMode属性为Zoom。(zoom:缩放;clip剪短;stret…...
3种方法设置PDF“打开密码”,总有一种适合你
PDF文件是我们工作中经常用到的文件之一,对于重要的文件,设置“打开密码”是一种很好的保护方式。下面就来说说,设置PDF“打开密码”有哪三种方法? 方法一:在线网站加密 市面上有很多可以直接在线上加密PDF文件的产品…...
-计算机网络(笔记))
第三章 数据链路层(点到点的传输服务)-计算机网络(笔记)
计算机网络 第三章 数据链路层(点到点的传输服务) 数据链路层属于计算机网络的低层。数据链路层使用的信道主要有以下两种类型: (1)点到点信道。这种信道使用一对一的点到点通信方式。 (2)广…...

volatile关键字与CAS机制
volatile关键字 volatile关键字可以对类的成员变量与静态变量进行修饰 volatile关键字的作用 1.保证被修饰属性的可见性,被修饰后的属性如果被更改后其他线程是会立即可见的 2.保证被修饰属性的有序性,被修饰后的属性禁止修改指令执行的顺序 注意:volatile关键字不能保证属性…...

LeetCode题解 动态规划(四):416 分割等和子集;1049 最后一块石头的重量 II
背包问题 下图将背包问题做了分类 其中之重点,是01背包,即一堆物件选哪样不选哪样放入背包里。难度在于,以前的状态转移,多只用考虑一个变量,比如爬楼梯的阶层,路径点的选择,这也是能用滚动数组…...

【FFMPEG源码分析】从ffplay源码摸清ffmpeg框架(二)
demux模块 从前面一篇文章中可以得知,demux模块的使用方法大致如下: 分配AVFormatContext通过avformat_open_input(…)传入AVFormatContext指针和文件路径,启动demux通过av_read_frame(…) 从AVFormatContext中读取demux后的audio/video/subtitle数据包…...
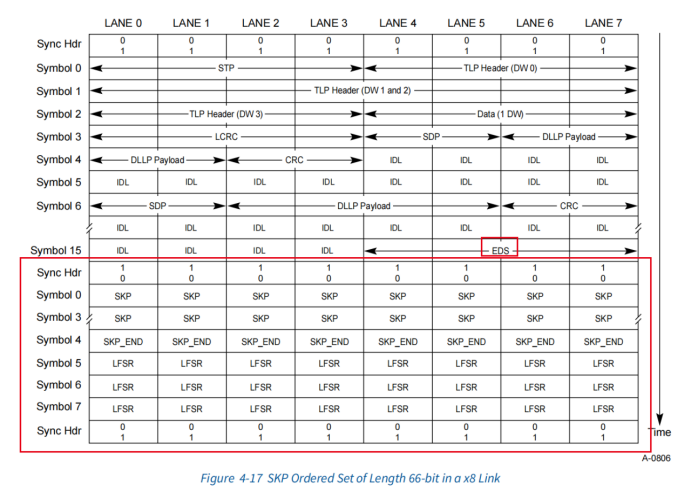
PCIE 学习笔记(入门简介)
PCIE 学习笔记书到用时方恨少啊,一年前学PCIE的笔记,再拿出来瞅瞅。发到博客上,方便看。PCIE基础PCIE和PCI的不同PCIE采用差分信号传输,并且是dual-simplex传输——每条lane上有TX通道和RX通道,所以每条lane上的信号是…...
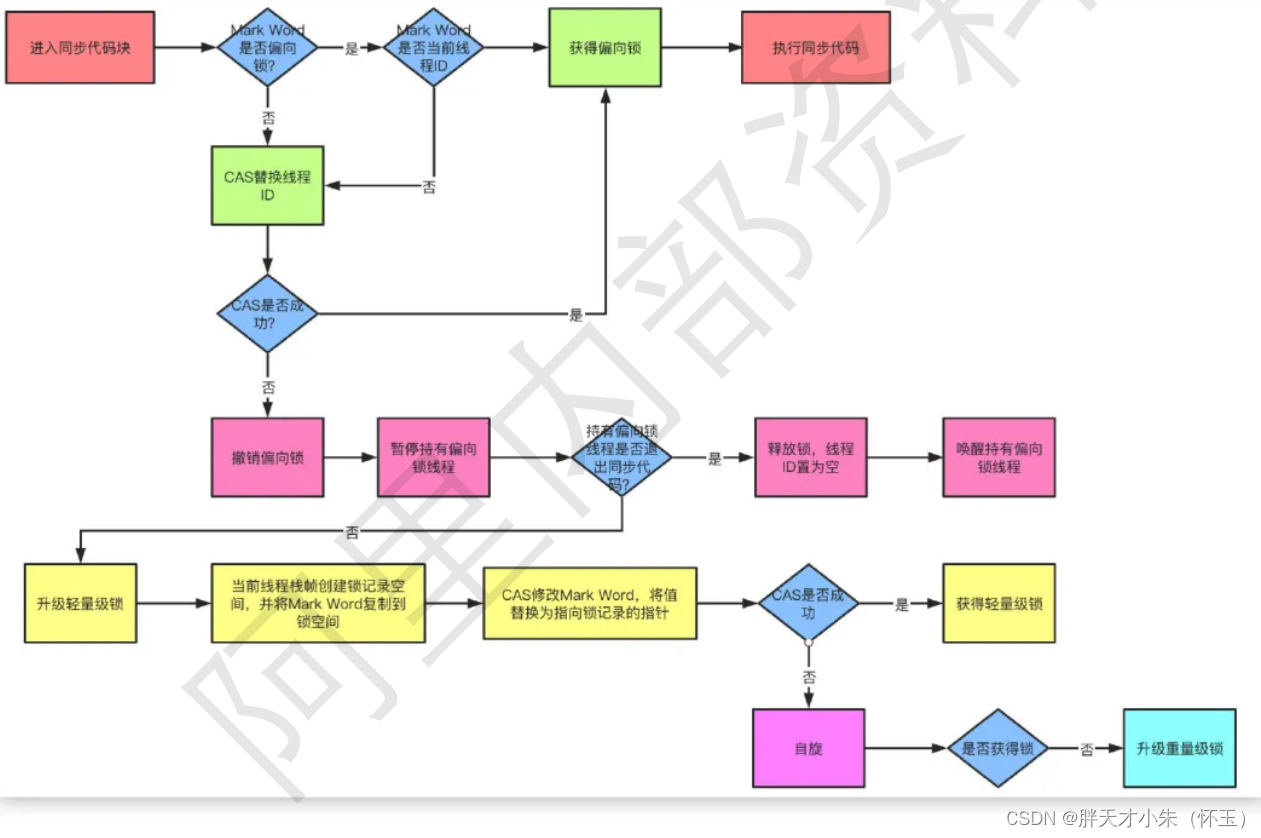
锁的优化机制了解嘛?请进!
点个关注,必回关 文章目录自旋锁:自适应锁:锁消除:锁粗化:偏向锁:轻量级锁:从JDK1.6版本之后,synchronized本身也在不断优化锁的机制,有些情况下他并不会是一个很重量级的…...

5.点赞功能 Redis
Redis(1)简介Redis 是一个高性能的 key-value 数据库原子 – Redis的所有操作都是原子性的。多个操作也支持事务,即原子性,通过MULTI和EXEC指令包起来。非关系形数据库数据全部存在内存中,性能高。(2&#…...
)
Java序列化和反序列化(详解)
一、理解Java序列化和反序列化 Serialization(序列化):将java对象以一连串的字节保存在磁盘文件中的过程,也可以说是保存java对象状态的过程。序列化可以将数据永久保存在磁盘上(通常保存在文件中)。 deserialization(反序列化):将保存在磁…...

【刷题篇】链表(上)
前言🌈前段时间我们学习了单向链表和双向链表,本期将带来3道与链表相关的OJ题来巩固对链表的理解。话不多说,让我们进入今天的题目吧!🚀本期的题目有:反转单链表、链表的中间结点、合并两个有序链表反转单链…...

ConcurrentHashMap设计思路
ConcurrentHashMap设计思路Hashtable vs ConcurrentHashMapHashtable vs ConcurrentHashMap Hashtable 对比 ConcurrentHashMap Hashtable 与 ConcurrentHashMap 都是线程安全的 Map 集合Hashtable 并发度低,整个 Hashtable 对应一把锁,同一时刻&#…...

Unity基于GraphView的行为树编辑器
这里写自定义目录标题概述基于GitHub上:目前这只是做了一些比较基础的功能节点开发,仅仅用于学习交流,非完成品。项目GitHub连接:[https://github.com/HengyuanLee/BehaviorTreeExamples](https://github.com/HengyuanLee/Behavio…...
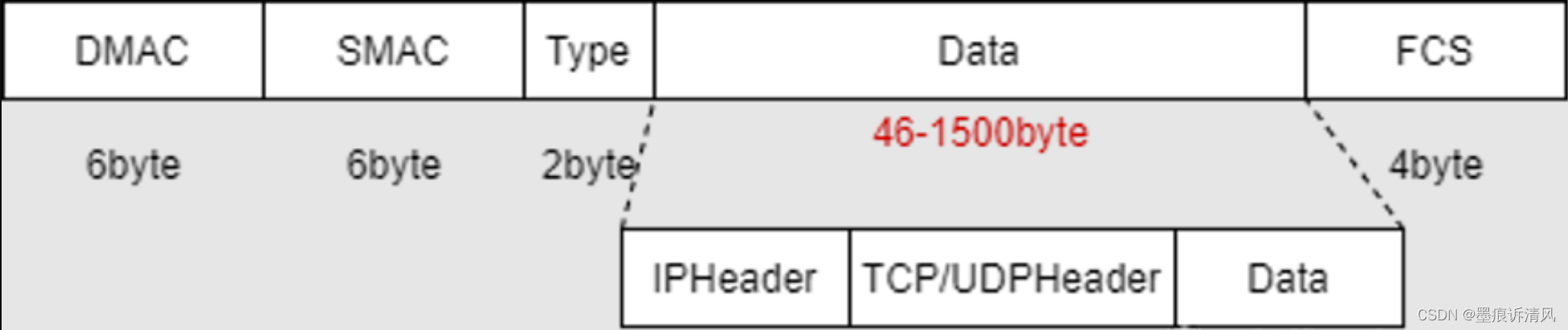
网络流量传输MTU解析
基本概念 以太网的链路层对数据帧的长度会有一个限制,其最大值默认是1500字节,链路层的这个特性称为MTU,即最大传输单元 Maximum Transmission Unit,最大传输单元,指的是数据链路层的最大payload,由硬件网…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
