数据库系统原理与实践 笔记 #7
文章目录
- 数据库系统原理与实践 笔记 #7
- 数据库设计和E-R模型(续)
- 转换为关系模式
- 具有简单属性的实体集的表示
- 复合属性
- 多值属性
- 联系集的表示
- 模式的冗余—合并
- 实体-联系设计问题
- 设计问题
- 联系属性的布局
- 扩展的E-R特性
- 特化
- 概化
- 属性继承
- 特化/概化的设计约束
- 聚集
- E-R图表示方法总结
- E-R设计方案
- UML
- E-R图与UML类图对比
- 关系数据库设计
- 好的关系设计的特点
- 设计选择1:更大的模式?
- 设计选择2:更小的模式?
- 有损分解
- 无损分解的例子
- 函数依赖
- 函数依赖和码
- 函数依赖是码的概化
- 函数依赖的使用
- 函数依赖相关术语
- 函数依赖集的闭包
- 函数依赖的路基蕴含
- 函数依赖的推理规则
- 属性闭包的应用
数据库系统原理与实践 笔记 #7
数据库设计和E-R模型(续)
转换为关系模式
- 一个符合E-R模式的数据库可以表示为一些关系模式的集合:
- 实体集和联系集都可以用表示数据库内容的统一的关系模式来表示
- 每个实体集合联系集独有一个特有的关系模式与其对应,并分配相应的名字
- 每个关系模式都有一些列,每个列多有唯一的名字
具有简单属性的实体集的表示
- 从强实体集转换而来的模式与强实体集具有相同属性、主码
- 从弱实体集转换的模式包含弱实体集的属性和表示强实体集的主码
- 该模式的主码由强实体集的主码与弱实体集的分辨符组合而成
复合属性
- 复合属性通过为每个子属性创建单独的属性
- 实体集instructor有复合属性name:由first_name, middle_name和last_name构成
- 转化成关系模式后,该实体集具有name_first_name,name_middle_name和name_last_name
多值属性
- 实体集E的多值属性M用一个独立的模式EM表示
- 模式EM包含对应于的E主码及多值属性M的属性
- 多值属性的每个值映射到关系模式EM的每一个独立元组
- 不需要建立一个对应于实体集的模式,只需创建一个对应于多值属性的关系即可
联系集的表示
- 联系集关系模式属性的选择
- 联系集主码选择:二元联系集主码选择、多元联系集主码选择
- 注意:需要为联系集的属性建立外码约束
模式的冗余—合并
- 多对一和一对多的联系集的模式,如果“多”方参与是全部的,那么可以将 “多”方实体集和联系集的模式合并成单个包含两个模式所有属性并集的关系模式
- 合并后模式加入原联系集的外码约束
- 如果“多”方参与是部分的,也可以通过使用空值来进行模式合并。转换为关系模式时,联系集中 “一”方的相关属性应注意不能设置为not null
- 在一对一联系的情况下,联系集的关系模式可以跟参与联系的任何一个实体集的模式进行合并
- 一般而言,连接弱实体集与其标识强实体集之间的标识性联系集转换出的模式是冗余的
实体-联系设计问题
设计问题
-
常见错误:用一个实体集的主码作为另一个实体集的属性、将相关实体集的主码属性作为联系集的属性

-
如果注册信息还与其他实体集相联系,那么上述E-R设计更有效
-
一般而言,通过创建一个实体集可以将非二元联系集转换为二元联系集
-
所有的费二元联系集都可以用多个二元联系集来表示,但有时n元的联系集能够更清楚的表示几个参与的实体集之间的联系
联系属性的布局
- 设计时将联系集的描述性属性作为联系集的属性还是实体集的属性这一选择应由映射基数约束决定
扩展的E-R特性
特化
- 自顶向下设计过程:从初始实体集到一系列不同层次的实体子集的细化(具体化)
- 在实体集内部进行分组的过程称为特化
- 子集中的实体在某些方面区别于实体集中的其他实体:这些子集成为了较低层的实体集,可能具有高层实体集不具有的属性、或者参与到高层实体集不参与的实体集中
- 特化通过从特化实体指向另一个实体的空心箭头来表示
概化
- 自底向上设计过程:多个实体集根据共同具有的特征综合称一个较高层的实体集
- 概化是高层实体集与一个或多个底层时提及间的包含关系
- 概化是特化的逆过程,可互换使用
- 它们在E-R图中的表示是相同的,区别在于不同的出发点和目标
属性继承
- 属性继承—底层实体集继承了与其相关联的高层实体集的所有属性,并且继承地参与到其高层实体所参与的联系集中
特化/概化的设计约束
- 成员资格判断约束:条件/属性定义的、用户定义的:用户将实体指派给某个实体集
- 实体是否可以属于同一概化中的多个低层实体集的约束:不相交、重叠
- 完全性约束:定义高层实体集中的一个实体是否必须属性该概化的至少一个低层实体集:全部:每个高层实体必须属于一个低层实体集、部分:允许一些高层实体不属于任何低层实体集
- 默认部分概化
聚集
-
考虑我们之前看到的三元联系proj_guide,假设我们要记录某个项目中导师对学生的评价

-
为不引入冗余,用聚集来表示E-R模型,如下图所示:一个学生在一个指定的项目中由一个指定导师辅导;学生、导师、项目的组合可能有相关联的评价信息
E-R图表示方法总结


E-R设计方案
- 用实体或者属性表示一个对象
- 由实体集或联系集更好地表达现实世界的概念
- 强/弱实体集的使用
- 概化/特化的使用—有助于模块化设计
- 聚类的使用—将聚集实体集作为单一单元,不必考虑其内部结构
UML
- UML(Unified Modeling Language): 统一建模语言
- UML包含了将整个软件系统图形化的很多组件
- UML类图与E-R图类似,仅有一些不同
E-R图与UML类图对比


关系数据库设计
好的关系设计的特点
设计选择1:更大的模式?
-
通过E-R图转换得出一组关系模式后
-
选择1:把一些关系模式合并为更大的关系,例如inst_dept(ID,name,salary,dept_name,building,budget)

-
如果通过E-R模型转换得出如下的两个关系模式:sec_class(sec_id, building, room_number) and section(course_id, sec_id, semester, year)
-
那么在逻辑设计中,我们可以将上述两个关系合并为如下关系:section(course_id, sec_id, semester, year, building, room_number),这样的关系模式不会产生数据冗余
设计选择2:更小的模式?
- 如果通过E-R模型转换得出inst_dept关系模式,那么在逻辑设计中,我们可以将其分解为两个关系模式:instructor(ID, name, salary, dept_name),department(dept_name, building, budget)
- 这样可以避免(building, budget)的数据冗余
- 可以通过如下一条规则:dept_name确定(building,budget)数据,即保持函数依赖:dept_name → \rightarrow →building,budget
- 由于dept_name在inst_dept关系中不是主码,因此需要将其拆分为更小的关系模式
- 并不是所有的关系模式拆分都是有益的:
- 例如,将employee(ID,name, street)分解为employee_attr1(ID, name)和employee_attr2(name, street, city, salary)
- name无法作为employee_attr2关系的主码,有可能会重名:无法通过分解出的employee_attr1和employee_attr2重建(自然连接)得出原始关系
- 我们称无法通过自然连接重建原始关系元组的分解为有损分解
有损分解

无损分解的例子
-
无损分解(lossless decomposition)
-
R = ( A , B , C ) R=(A,B,C) R=(A,B,C)的分解: R 1 = ( A , B ) , R 2 = ( B , C ) R_1=(A,B),\ R_2=(B,C) R1=(A,B), R2=(B,C)

-
r = ∏ A , B ( r ) ⋈ ∏ B , C ( r ) r = \prod_{A,B}(r)\bowtie \prod_{B,C}(r) r=∏A,B(r)⋈∏B,C(r)
-
inst_dept分解为instructor和department关系是无损分解
函数依赖
- 假设 r ( R ) r(R) r(R)是一个关系模式, α ⊆ R , β ⫅ R \alpha \subseteq R,\beta \subseteqq R α⊆R,β⫅R,模式R上的函数依赖:
α → β \alpha\rightarrow\beta α→β - 成立的条件是:如果对于任意关系实例r中任意两个元组 t 1 t_1 t1和 t 2 t_2 t2,如果两者的属性(集) α \alpha α 的值相同,那么它们的属性(集) β \beta β 取值也相同。也就是:
t 1 [ α ] = t 2 [ α ] ⇒ t 1 [ β ] = t 2 [ β ] t_1[\alpha] =t_2[\alpha] \Rightarrow t_1[\beta]=t_2[\beta] t1[α]=t2[α]⇒t1[β]=t2[β] - 称 α \alpha α函数确定 β \beta β, β \beta β函数依赖于 α \alpha α
函数依赖和码
- 超码:在某关系中,若一个或多个属性的集合 { A 1 , A 2 , . . . , A n } \{A_1, A_2,...,A_n\} {A1,A2,...,An},函数决定该关系中的其它全部属性,则称该关系的超码
- 候选码:若集合 { A 1 , A 2 , . . . , A n } \{A_1, A_2, ..., A_n\} {A1,A2,...,An}的任何真子集均不能函数决定该关系中的其它属性,则此时 { A 1 , A 2 , . . . , A n } \{A_1, A_2, ..., A_n\} {A1,A2,...,An}是最小的超码,即候选码
- 外码:若关系模式R中属性或属性组X是另一个关系模式的主码,则称X是R的外码
函数依赖是码的概化
- 函数依赖允许我们表达超码不能表达的约束,考虑下面的模式:inst_dept(ID, name, salary, dept_name, building, budget)
函数依赖的使用
- 函数依赖在关系实例和关系模式上的体现区别:
- 如果关系实例r咋函数依赖集F上合法,则称r满足F
- 如果模式R上的所有合法关系实例都满足函数依赖集F,我们说F在关系模式R上成立
- 注意:即使函数依赖并没有对关系模式 r ( R ) r(R) r(R)的所有合法实例成立,这个关系模式的其中一个具体实例r可能满足函数依赖
函数依赖相关术语
- 有些函数依赖被称为平凡(trivial) 的因为它们在所有关系中都是满足的
- 例如:name → \rightarrow →name,ID,name → \rightarrow →ID
- 通常,如果 β ⊆ α \beta \subseteq \alpha β⊆α,那么 α → β \alpha \rightarrow \beta α→β是平凡的函数依赖
- α → β \alpha\rightarrow\beta α→β,但 β ⊈ α \beta\nsubseteq\alpha β⊈α,则称 α → β \alpha\rightarrow\beta α→β是非平凡的函数依赖
- 若 α → β \alpha\rightarrow\beta α→β,则称 α \alpha α为决定因素
- 函数依赖 α → β \alpha\rightarrow\beta α→β称为部分依赖的条件是:存在 α \alpha α的真子集 γ \gamma γ,使得 γ → β \gamma\rightarrow\beta γ→β
函数依赖集的闭包
- 从给定函数依赖集f能够推导出的所有函数依赖的集合,我们称之为F集合的闭包
- 我们用 F + F^+ F+来表示函数依赖集F的闭包
函数依赖的路基蕴含
- 给定关系模式 r ( R ) r(R) r(R),如果 r ( R ) r(R) r(R)的每个满足F的实例也满足某个函数依赖f,则R上的函数依赖f逻辑蕴含于r上的函数依赖集F
- 已知关系R上的函数依赖集T、F,如果对于该关系中满足F的每一个关系实例都满足T,则称函数依赖集F逻辑蕴涵函数依赖集F
函数依赖的推理规则
- Armstrong公理:
- 如果 β ⊆ α \beta\subseteq\alpha β⊆α,则有 α → β \alpha\rightarrow\beta α→β(自反律)
- 如果 α → β \alpha\rightarrow\beta α→β,则有 γ α → γ β \gamma\alpha\rightarrow\gamma\beta γα→γβ(增补律)
- 如果 α → β \alpha\rightarrow\beta α→β及 β → γ \beta\rightarrow\gamma β→γ,则有 α → γ \alpha\rightarrow\gamma α→γ(传递律)
- 附加定理:
-
如果 α → β \alpha\rightarrow\beta α→β及 α → γ \alpha\rightarrow\gamma α→γ,则有 α → β γ \alpha\rightarrow\beta\gamma α→βγ(合并律)
-
如果 α → β γ \alpha\rightarrow\beta\gamma α→βγ,则有 α → β \alpha\rightarrow\beta α→β及 α → γ \alpha\rightarrow\gamma α→γ(分解律)
-
如果 α → β \alpha\rightarrow\beta α→β及 γ β → δ \gamma\beta\rightarrow\delta γβ→δ,则有 α γ → δ \alpha\gamma\rightarrow\delta αγ→δ(伪传递律)
-
属性闭包的应用
- 超码的判断
- 验证函数依赖
- 计算F的闭包
相关文章:

数据库系统原理与实践 笔记 #7
文章目录 数据库系统原理与实践 笔记 #7数据库设计和E-R模型(续)转换为关系模式具有简单属性的实体集的表示复合属性多值属性联系集的表示模式的冗余—合并 实体-联系设计问题设计问题联系属性的布局 扩展的E-R特性特化概化属性继承特化/概化的设计约束聚集E-R图表示方法总结E-…...

【CesiumJS】(1)Hello world
介绍 Cesium 起源于2011年,初衷是航空软件公司(Analytical Graphics, Inc.)的一个团队要制作世界上最准确、性能最高且具有时间动态性的虚拟地球。取名"Cesium"是因为元素铯Cesium让原子钟非常准确(1967年,人们依据铯原子的振动而对…...

Docker 学习路线 5:在 Docker 中实现数据持久化
Docker 可以运行隔离的容器,包括应用程序和其依赖项,与主机操作系统分离。默认情况下,容器是临时的,这意味着容器中存储的任何数据在终止后都将丢失。为了解决这个问题并在容器生命周期内保留数据,Docker 提供了各种数…...
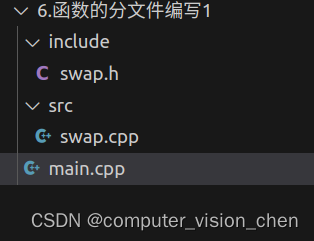
linux下使用vscode对C++项目进行编译
项目的目录结构 头文件swap.h 在自定义的头文件中写函数的声明。 // 函数的声明 void swap(int a,int b);swap.cpp 导入函数的声明,写函数的定义 #include "swap.h" // 双引号表示自定义的头文件 #include <iostream> using namespace std;// 函…...
LangChain+LLM实战---ChatGPT的即时插件套件制作
英文原文:Instant Plugins for ChatGPT: Introducing the Wolfram ChatGPT Plugin Kit 在一分钟内构建一个新插件 几周前,我们与OpenAI合作发布了Wolfram插件,使ChatGPT可以使用Wolfram语言和Wolfram|Alpha作为工具,在ChatGPT内部…...

包装印刷行业万界星空科技云MES解决方案
印刷业的机械化程度在国内制造行业内算是比较高的,不算是劳动密集型企业。如书本的装订、包装的模切、烫金、糊盒等都已经有了全自动设备。印刷厂除了部分手工必须采用人工外,大部分都可以采用机器,也就意味着可以由少量工人生产出大量产品。…...

Python教程---计算机语言简介
1.计算机编程语言的发展历程 计算机语言发展经历了三个阶段: 机器语言 - 机器语言通过二进制编码来编写程序,打孔织带机。 - 执行效率好,编写起来太麻烦 符号语言(汇编) - 使用符号来代替机器码 - 编写程序时…...
rhcsa-文件内容显示
浏览普通文件内容 浏览文件的命令 命令常用选项说明cat -n 对输出内容中的所有行标注行号 -b 对输出内容中的非空行标注行号 查看文件的内容head-num 指定需要显示文件num行的内容默认查看文前十行的内容tail -num 指定需要显示文件num行的内容 -f 使tail不停的去读取显示文…...

宠物养成猫狗商城门店问诊档案流量主小程序开发
宠物养成猫狗商城门店问诊档案流量主小程序开发 猫狗宠物养成商城门店问诊档案流量主小程序开发,这是一个充满趣味性和创新性的项目。通过将宠物养成游戏与商城、问诊服务、社交功能等相结合,为用户提供一站式的宠物养育体验。 在宠物养成方面&#x…...
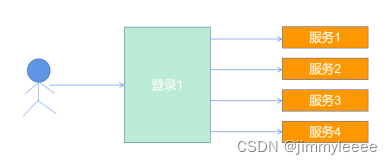
应用安全四十二:SSO安全
一、什么是SSO SSO是单点登录(Single Sign On)的缩写,是指在多个应用系统中,用户只需要登录一次就可以访问所有相互信任的应用系统。这种方式减少了由登录产生的时间消耗,辅助了用户管理,是比较流行的企业业务整合的解决方案之一。 身份验证过程依赖于双方之间的信任关…...

【行云流水线实践】基于“OneBuild”方法对镜像进行快速装箱 | 京东云技术团队
在云原生领域,无论使用哪种编排调度平台,Kubernetes,DockerSwarm,OpenShift等,业务都需要基于镜像进行交付,我们在内部实践“Source-to-image”和链式构建,总而总结出“OneBuild”模式。 其核心…...
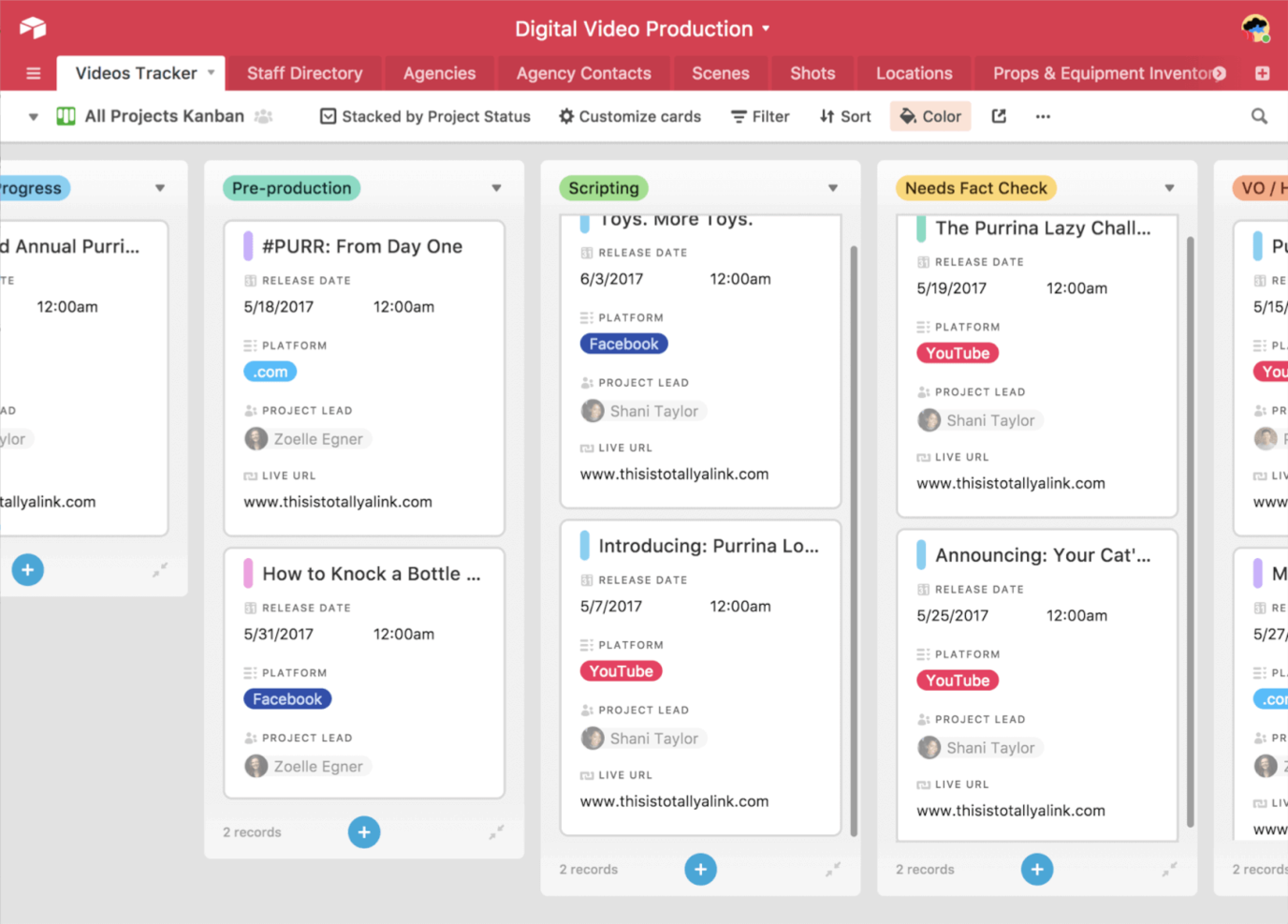
软件开发必备神器!一文读懂10款热门看板工具推荐!
看板(Kanban)是一种流行的框架,用于实施敏捷和DevOps软件开发。它要求实时沟通每个人的能力,并全面透明地展示正在进行的工作。工作项目在看板上以可视化方式表示,使项目经理和所有团队成员可以随时查看每个工作的状态…...

怎样提取视频提取的人声或伴奏?
有些小伙伴们进行音视频创作时,可能会需要提取音频的人声或者是伴奏。这里给大家推荐一个音分轨人声分离软件,支持一键提取音频人声和一键提取伴奏功能,可批量导入文件同步提取,简单高效,是音视频创作者的不二选择&…...

SpringBoot概述
SpringBoot是Spring提供的一个子项目,用于快速构建Spring应用程序。 SpringFramework:核心功能SpringData:数据获取SpringSecurity:认证授权SpringAMQP:消息传递SpringCloud:服务治理 SpringBoot新特性&…...
深度学习框架TensorFlow.NET环境搭建1(C#)
测试环境 visual studio 2017 window10 64位 测试步骤如下: 1 新建.net framework控制台项目,工程名称为TensorFlowNetDemo,.net framework的版本选4.7.2,如下图: 2 分别安装TensorFlow.NET包(先装)和SciSharp.…...
Git客户端软件 Tower mac中文版特点说明
Tower mac是一款Mac OS X系统上的Git客户端软件,它提供了丰富的功能和工具,帮助用户更加方便地管理和使用Git版本控制系统。 Tower mac软件特点 1. 界面友好:Tower的界面友好,使用户能够轻松地掌握软件的使用方法。 2. 多种Git操…...
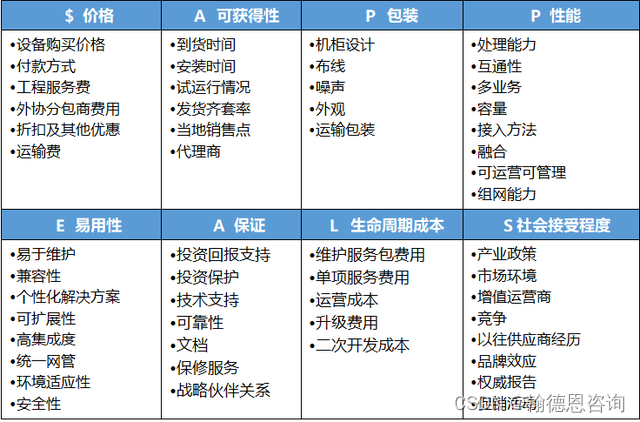
详解IPD需求分析工具$APPEALS
够让企业生存下去的是客户,所以,众多企业提出要“以客户为中心”,那如何做到以客户为中心?IPD中给出的答案是需求管理。 需求管理流程,是IPD(集成管理开发)体系中的四大支撑流程之一࿰…...

318. 最大单词长度乘积
这道题求没有重复字母的两个字符串的最大长度乘积 重点在于怎么判断两个字符串没有重复字母 题目中只有小写字母,最多26个,于是想到使用26位二进制数来代表每一个字符串 有哪个字母就在对应位置设1 这个转换使用的是num | 1 << (c-a); 对字符串中的…...
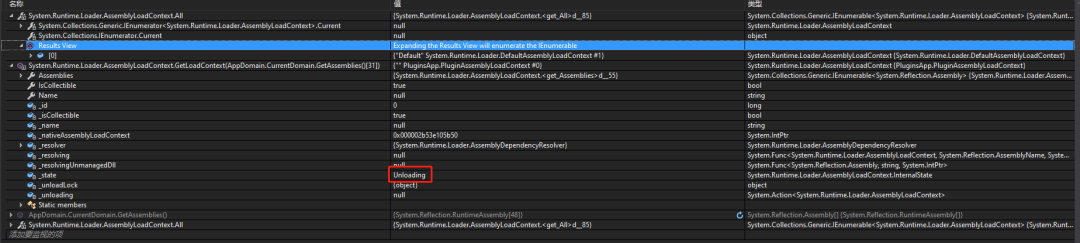
.NET Core 中插件式开发实现
在 .NET Framework 中,通过AppDomain实现动态加载和卸载程序集的效果;但是.NET Core 仅支持单个默认应用域,那么在.NET Core中如何实现【插件式】开发呢? 一、.NET Core 中 AssemblyLoadContext的使用 1、AssemblyLoadContext简…...

并查集模版以及两道例题
💯 博客内容:并查集 😀 作 者:陈大大陈 🚀 个人简介:一个正在努力学技术的准C后端工程师,专注基础和实战分享 ,欢迎私信! 💖 欢迎大家:这里是C…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
