线性代数之 伪逆矩阵
目录
一、伪逆矩阵
◼ A的伪逆矩阵与SVD
◼ 用Python代码计算A的伪逆矩阵
◼ 笔算A的伪逆矩阵
一、伪逆矩阵
◼ A的伪逆矩阵与SVD
逆矩阵并不总是存在,即使是方阵。然而,对于非正方形矩阵,存在一个伪逆矩阵,也叫摩尔-彭罗斯逆矩阵。
例如,矩阵A是m×n。使用伪逆矩阵A^+,我们可以进行以下转换。
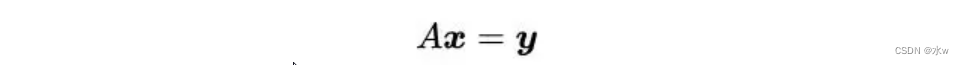
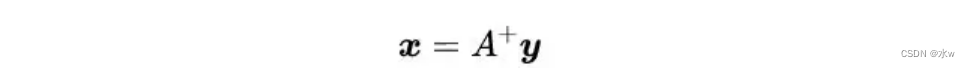
我们定义伪逆矩阵A^+为:

V和U来自奇异值分解。

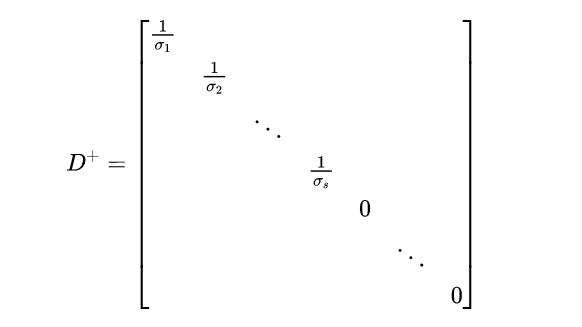
我们通过转置Σ和所有对角元素的逆得到D^+。假设Σ的定义如下:

那么D+的定义如下:
现在,我们可以看到A^+A的原理:
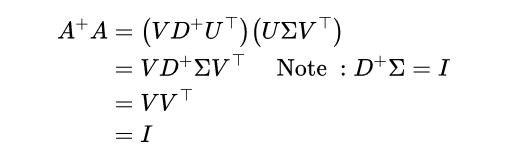
以同样的方式,AA^+ = I。
综上所述,如果我们能够对矩阵A进行奇异值分解,我们就可以通过VD^+UT来计算A^+,这是一个A的伪逆矩阵。
对于任意一个矩阵A,A的伪逆矩阵必然存在,且必然满足以下四个条件:

这四个条件(性质)蕴含了一个事情:AA^+必然是一个效果等同单位矩阵I、但又不是单位矩阵I的矩阵。
伪逆矩阵的极限形式定义:

伪逆矩阵更加常用的定义(基于SVD奇异值分解)
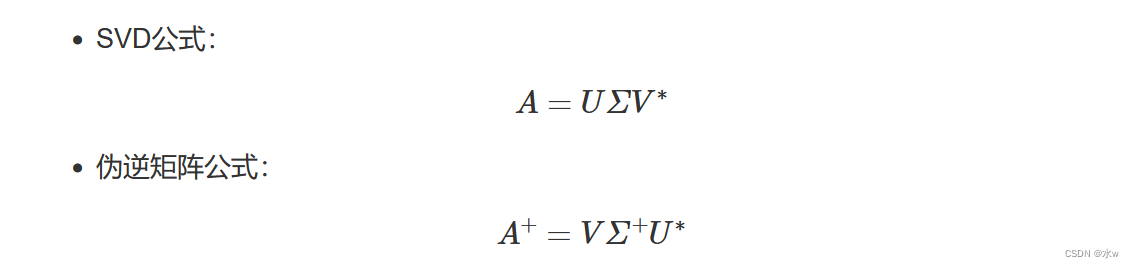
这个公式要注意的是中间的![]() 的求法。因为
的求法。因为![]() 是一个对角线矩阵,但又不一定是方阵,所以计算它的伪逆矩阵的步骤是特殊又简单的:
是一个对角线矩阵,但又不一定是方阵,所以计算它的伪逆矩阵的步骤是特殊又简单的:
-
将对角线上的元素取倒数
-
再将整个矩阵转置一次
◼ 用Python代码计算A的伪逆矩阵
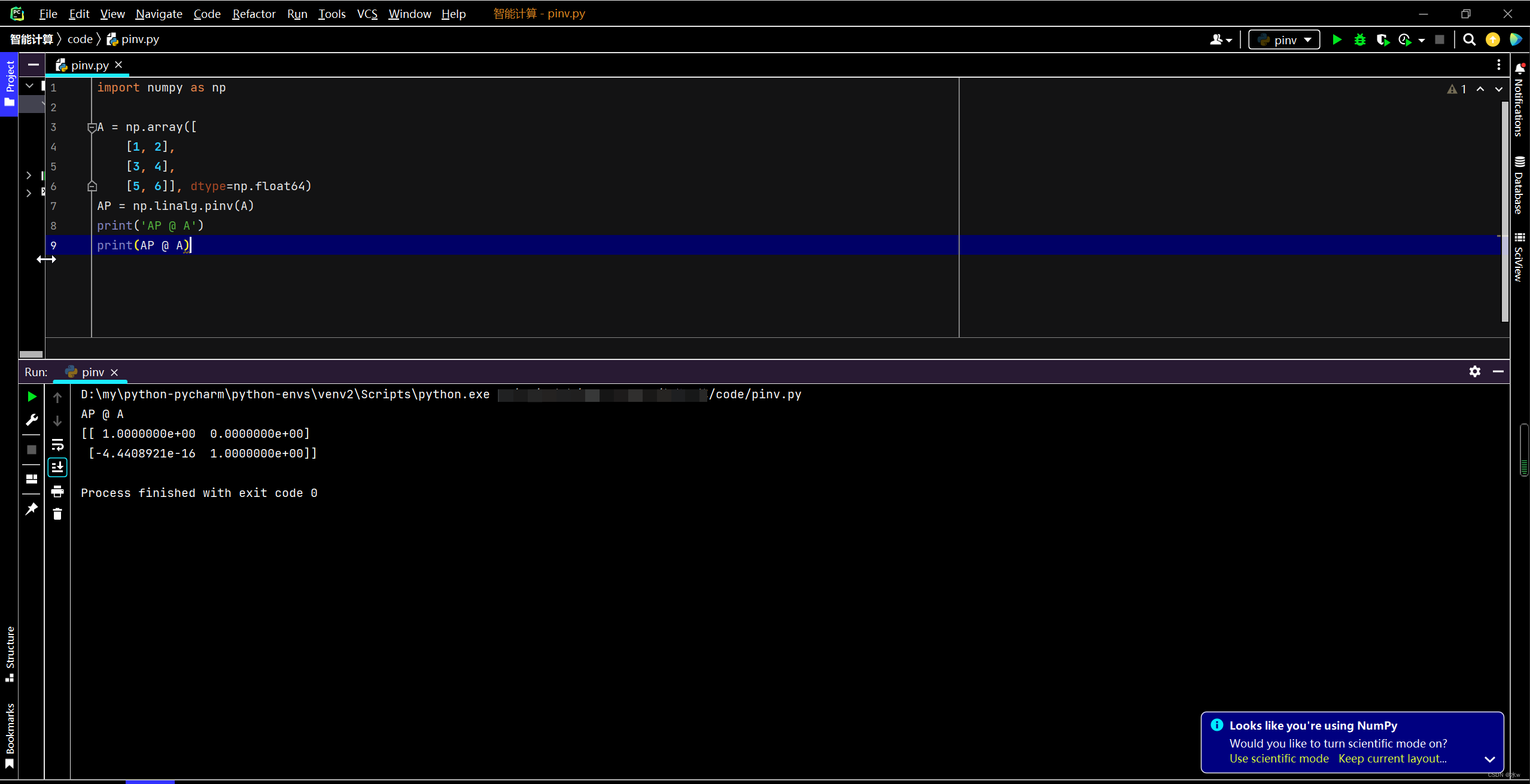
让我们用Numpy试试伪逆矩阵吧,
import numpy as npA = np.array([[1, 2],[3, 4],[5, 6]], dtype=np.float64)
AP = np.linalg.pinv(A)
print('AP @ A')
print(AP @ A)下面是输出结果:
◼ 笔算A的伪逆矩阵
我们把矩阵 A 定义为:
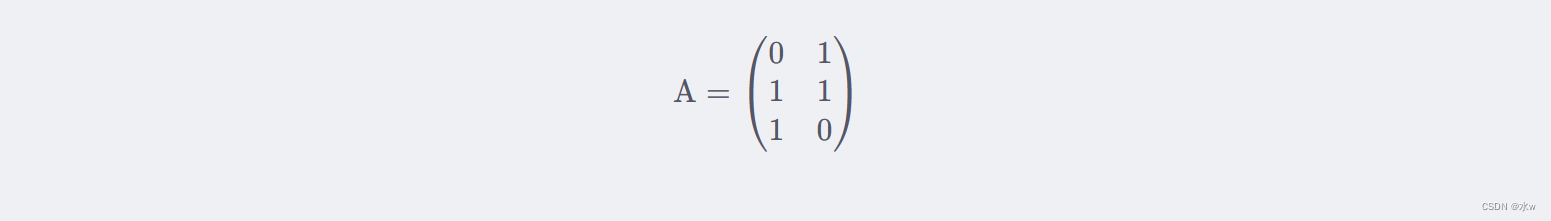
我们首先求出 A^TA 和 AA^T ,
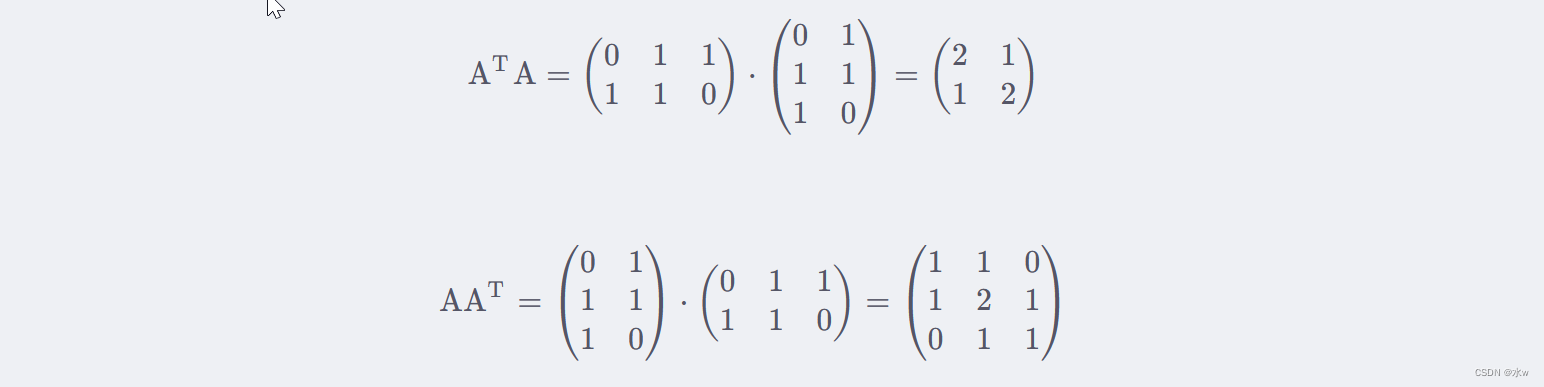
进而求出 A^TA 的特征值和特征向量: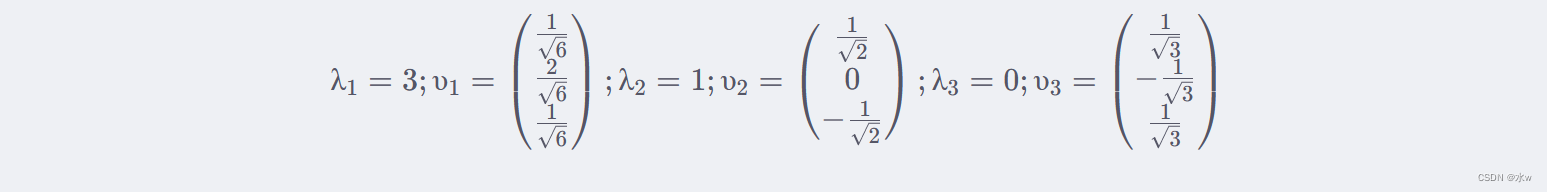
利用 Aνi=σiυi,i=1,2 求奇异值: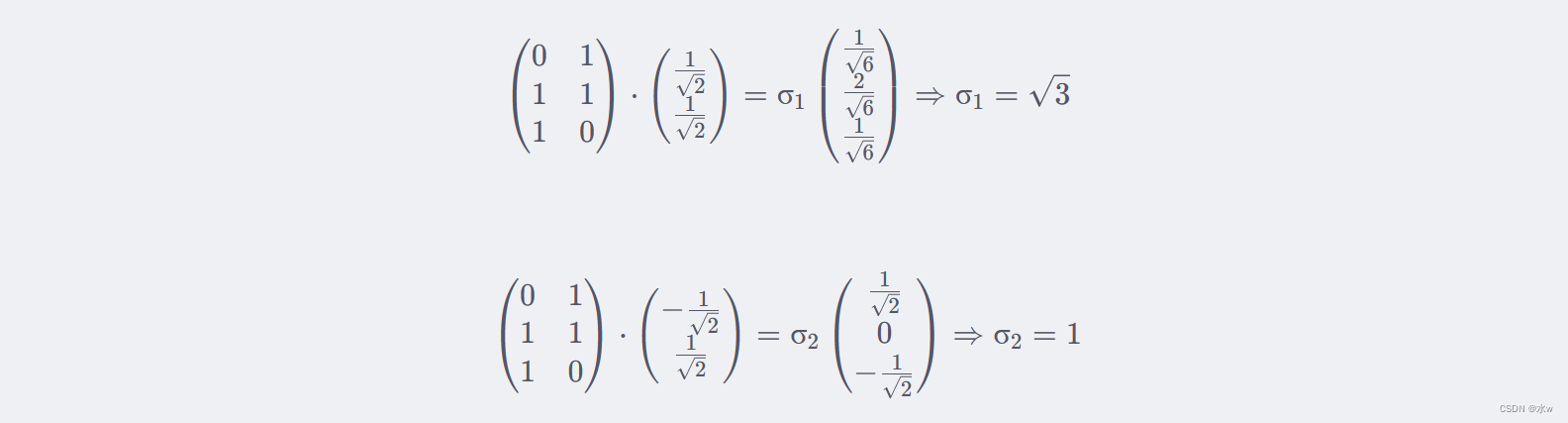
当然,我们也可以用 σ i =sqrt{ λ i },直接求出奇异值为sqrt{3} 和 1。最终,可以得到 A 的奇异值分解为:
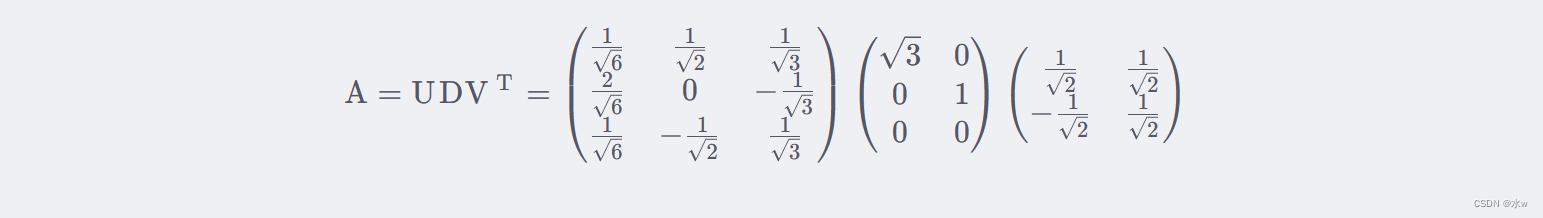
其中,矩阵 U ,D和 V 是矩阵 A奇异值分解后得到的矩阵。对角矩阵 D的伪逆 D^+ 是其非零元素取倒数之后再转置得到的。所以可以得到 A 的伪逆为:
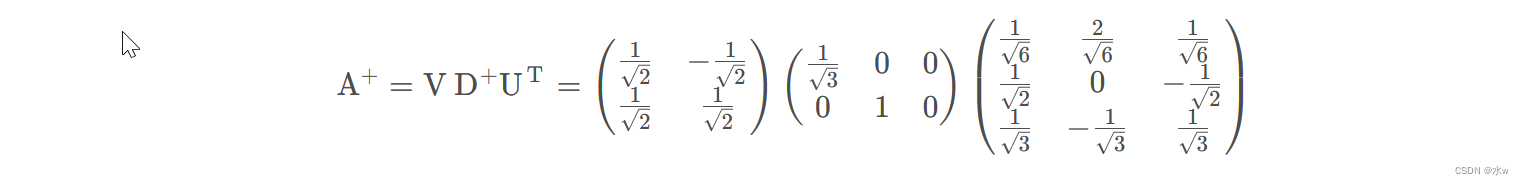
相关文章:
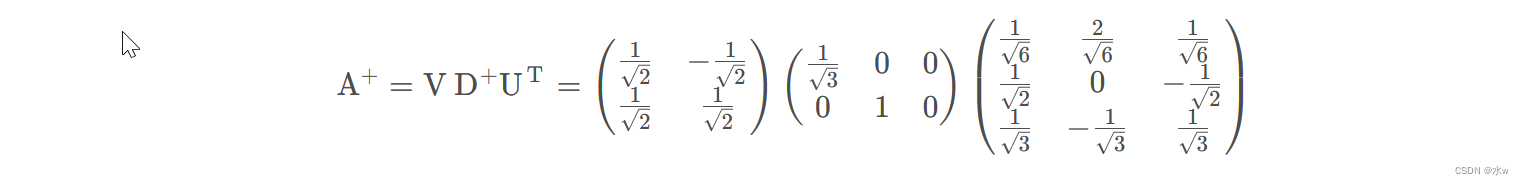
线性代数之 伪逆矩阵
目录 一、伪逆矩阵 ◼ A的伪逆矩阵与SVD ◼ 用Python代码计算A的伪逆矩阵 ◼ 笔算A的伪逆矩阵 一、伪逆矩阵 ◼ A的伪逆矩阵与SVD 逆矩阵并不总是存在,即使是方阵。然而,对于非正方形矩阵,存在一个伪逆矩阵,也叫摩尔-彭罗斯…...

【3D图像分割】基于Pytorch的VNet 3D 图像分割5(改写数据流篇)
在这篇文章:【3D 图像分割】基于 Pytorch 的 VNet 3D 图像分割2(基础数据流篇) 的最后,我们提到了: 在采用vent模型进行3d数据的分割训练任务中,输入大小是16*96*96,这个的裁剪是放到Dataset类…...
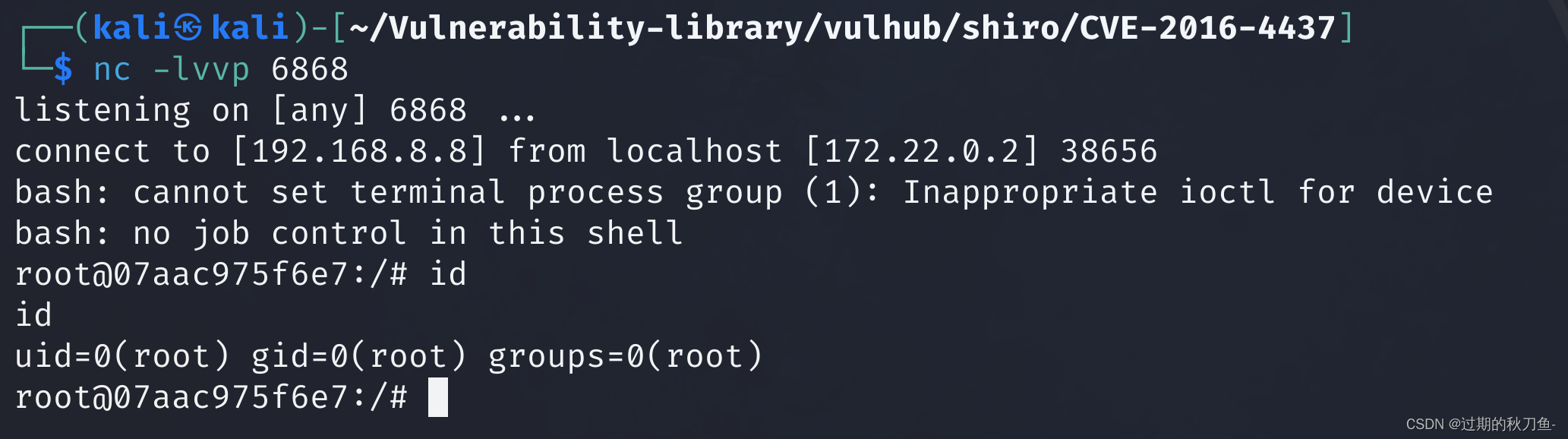
【漏洞复现】Apache_Shiro_1.2.4_反序列化漏洞(CVE-2016-4437)
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现1、基础环境2、漏洞分析3、漏洞验证 说明内容漏洞编号CVE-2016-4437漏洞名称Apache_Shiro_1.2.4_反序列化漏洞漏洞评级…...

Mac连接linux的办法(自带终端和iterm2)
1. 使用Mac自带终端Terminal 1.1 点击右上角的聚焦搜索,再输入终端 1.2 查找linux系统的ip地址 在虚拟机里输入如下命令,找到蓝色区域的就是ip地址 ip addr 如果没有显示ip地址,可以重新安装一下虚拟机,之后确保以太网的连接是打…...
js调整table表格上下相邻元素顺序
有时候我们会遇到要通过箭头控制table表格上下顺序的需求,如下: 点击向下就将该元素下移一位,下面的一位元素就移上来,点击向上就将该元素上移一位,上面的一位元素就移下来,也就是相邻元素互换位置顺序: <el-table :data="targetTable" border style=&quo…...
基于ruoyi框架项目-部署到服务器上
基于ruoyi框架项目-部署到服务器上 文章目录 基于ruoyi框架项目-部署到服务器上1.前端vue编译,后的dist下内容打包(前后端分离版本需要)2.后端打包成jar包(如果是thymeleaf仅需打包jar)3.上传到服务器目录下4. docker部…...
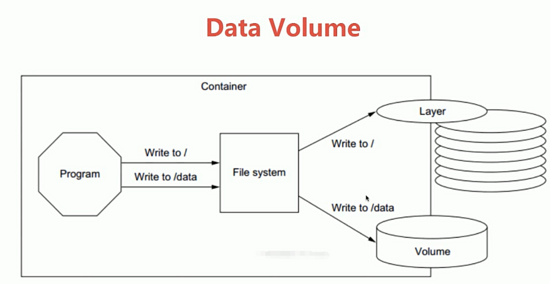
Docker 持久化存储和数据共享_Volume
有些容器会自动产生一些数据,为了不让数据随着 container 的消失而消失,保证数据的安全性。例如:数据库容器,数据表的表会产生一些数据,如果我把 container 给删除,数据就丢失。为了保证数据不丢失…...

万宾科技智能井盖监测仪器助力建设数字化城市
市政公共设施建设在近几年来发展迅速,市政设备的更新换代,资产管理等也成为其中的重要一项。在市政设施建设过程中,井盖也是不可忽视的,一方面,根据传统的管理井盖模式来讲,缺乏有效的远程监控管理方法和手…...
第十一章《搞懂算法:聚类是怎么回事》笔记
聚类是机器学习中一种重要的无监督算法,可以将数据点归结为一系列的特定组合。归为一类的数据点具有相同的特性,而不同类别的数据点则具有各不相同的属性。 11.1 聚类算法介绍 人们将物理或抽象对象的集合分成由类似 的对象组成的多个类的过程被称为聚…...
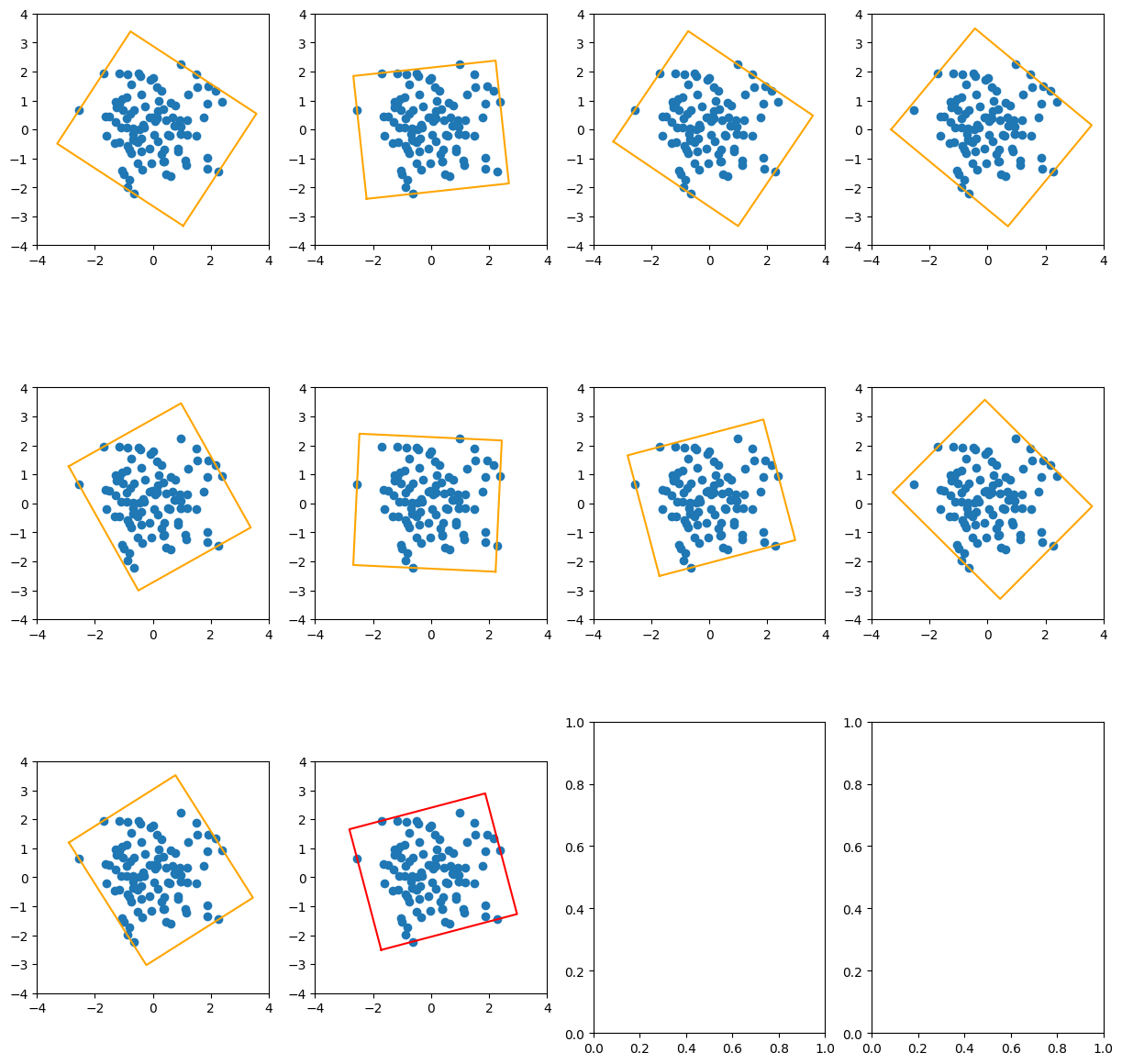
给定n个点或一个凸边形,求其最小外接矩形,可视化
这里写目录标题 原理代码 原理 求n个点的最小外接矩形问题可以等价为先求这n个点的凸包,再求这个凸包的最小外接矩形。 其中求凸包可以使用Graham-Scan算法 需要注意的是, 因为Graham-Scan算法要求我们从先找到凸包上的一个点,所以我们可以先…...

蓝桥杯每日一题2023.11.6
取位数 - 蓝桥云课 (lanqiao.cn) 题目描述 题目分析 由题意我们知道len中为现阶段长度,如果其与k相等也就是找到了正确的位数,否则就调用递归来进行搜索,每次搜索一位数。 #include <stdio.h> // 求x用10进制表示时的数位长度 int …...
V-REP和Python的联合仿真
机器人仿真软件 各类免费的的机器人仿真软件优缺点汇总_robot 仿真 软件收费么_dyannacon的博客-CSDN博客 课程地址 https://class.guyuehome.com/p/t_pc/course_pc_detail/column/p_605af87be4b007b4183a42e7 课程资料 guyueclass: 古月学院课程代码 旋转变换 旋转的左乘与…...

WPF布局控件之DockPanel布局
前言:博主文章仅用于学习、研究和交流目的,不足和错误之处在所难免,希望大家能够批评指出,博主核实后马上更改。 概述: DockPanel 位置子控件基于子 Dock 属性,你有 4 个选项停靠,左 (默认) &…...
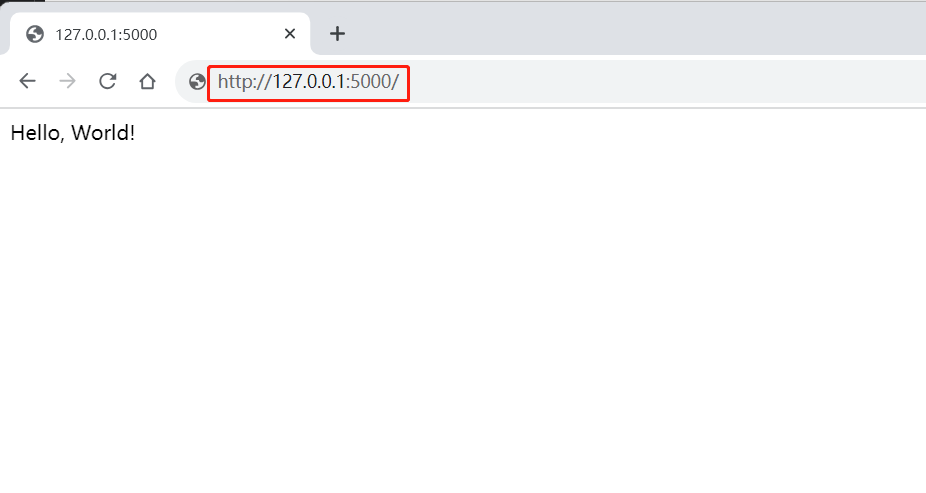
【实战Flask API项目指南】之二 Flask基础知识
实战Flask API项目指南之 Flask基础知识 本系列文章将带你深入探索实战Flask API项目指南,通过跟随小菜的学习之旅,你将逐步掌握Flask 在实际项目中的应用。让我们一起踏上这个精彩的学习之旅吧! 前言 当小菜踏入Flask后端开发的世界&…...
C++链接库std::__cxx11::basic_string和std::__1::basic_string链接问题总结)
Linux 编译链接那些事儿(02)C++链接库std::__cxx11::basic_string和std::__1::basic_string链接问题总结
1 问题背景说明 在自己的项目源码中引用libeasysqlite.so时编译成功,但运行时遇到问题直接报错,找不到符号 symbol:_ZN3sql5FieldC1ENSt3__112basic_stringIcNS1_11char_traitsIcEENS1_9allocatorIcEEEENS_10field_typeEi。 2 问题描述和解…...
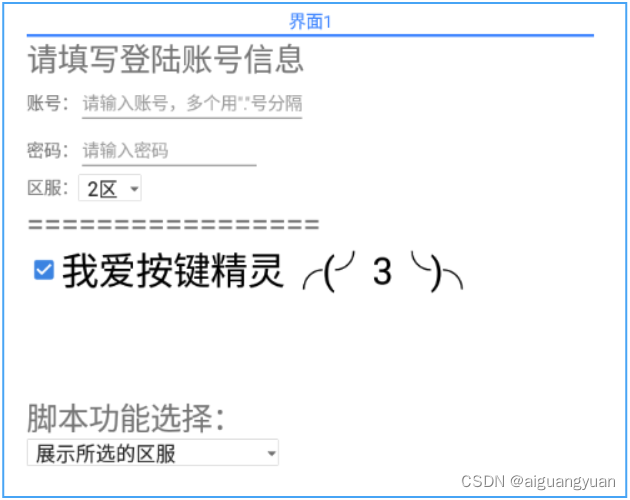
按键精灵中的UI界面操作
1. 按键精灵中UI界面常用的控件 1. 文字框 界面1: {标签页1:{文字框:{名称:"文字框1",显示内容:"显示内容",文字大小:0,高度:0,宽度:0,注释:"文字大小、高度、宽度是可选属性,如需使用默认值,可保持值为0或直接删除此属性&qu…...

dpdk 程序如何配置网卡收发包队列描述符配置?
问题描述 dpdk 程序在配置网卡队列时会涉及收发包队列描述符数量配置问题,收发包描述符的数量看似是一个简单的配置,却对转发性能有着一定的影响。实际业务程序中,收发包描述符大小配置一般参考 dpdk 内部示例程序配置进行,经验之…...

二蛋赠书七期:《云原生数据中台:架构、方法论与实践》
前言 大家好!我是二蛋,一个热爱技术、乐于分享的工程师。在过去的几年里,我一直通过各种渠道与大家分享技术知识和经验。我深知,每一位技术人员都对自己的技能提升和职业发展有着热切的期待。因此,我非常感激大家一直…...
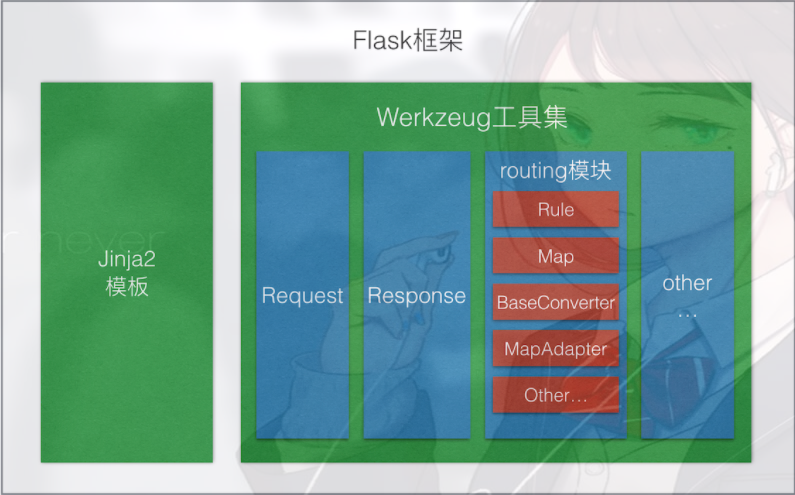
计算机毕设 基于大数据的服务器数据分析与可视化系统 -python 可视化 大数据
文章目录 0 前言1 课题背景2 实现效果3 数据收集分析过程**总体框架图****kafka 创建日志主题****flume 收集日志写到 kafka****python 读取 kafka 实时处理****数据分析可视化** 4 Flask框架5 最后 0 前言 🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升&a…...
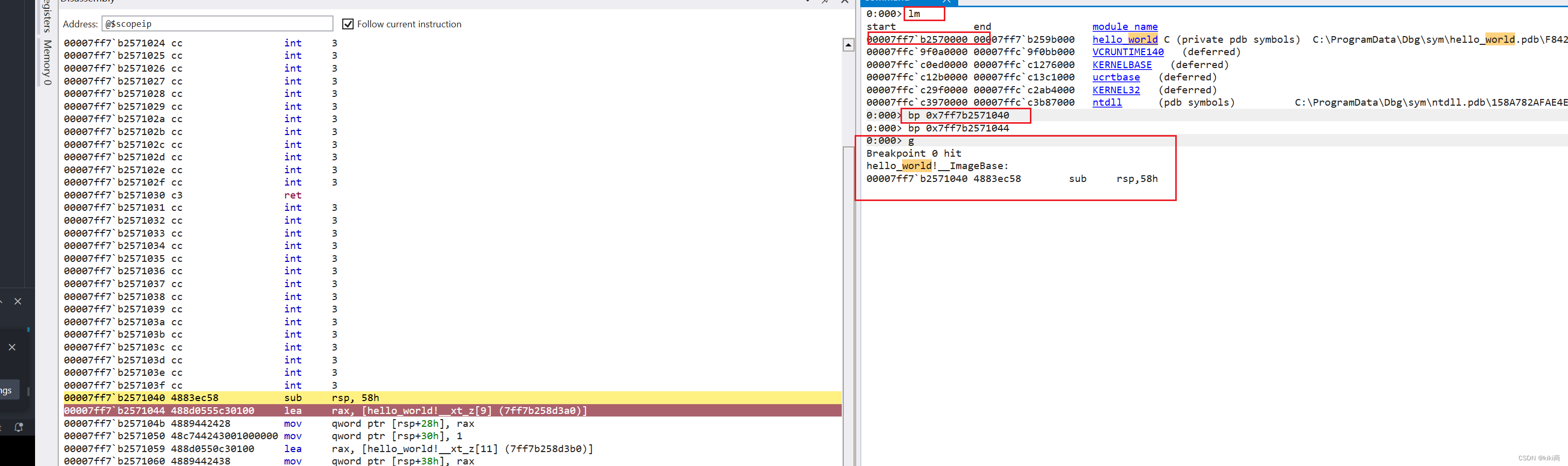
初识rust
调试下rust 的执行流程 参考: 认识 Cargo - Rust语言圣经(Rust Course) 新建一个hello world 程序: fn main() {println!("Hello, world!"); }用IDA 打开exe,并加载符号: 根据字符串找到主程序入口: 双击…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
