累计概率分布、概率分布函数(概率质量函数、概率密度函数)、度量空间、负采样(Negative Sampling)
这里写自定义目录标题
- 机器学习的基础知识
- 累计概率分布
- 概率分布函数
- 度量空间
- 负采样(Negative Sampling)
- 基于分布的负采样(Distribution-based Negative Sampling):
- 基于近邻的负采样(Neighbor-based Negative Sampling):
机器学习的基础知识
累计概率分布、概率分布函数(概率质量函数、概率密度函数)、度量空间、负采样(Negative Sampling)
累计概率分布
累计概率分布是指离散随机变量或连续随机变量的概率分布函数(Probability Distribution Function,简称PDF)在某个取值点之前的概率之和。
对于离散随机变量,累计概率分布函数(Cumulative Distribution Function,简称CDF)定义为在该点之前所有概率质量函数(Probability Mass Function,简称PMF)值的累加和。
对于连续随机变量,累计概率分布函数定义为在该点之前的概率密度函数(Probability Density Function,简称PDF)的积分。
以离散随机变量为例,设随机变量X具有概率质量函数P(X = x),则其累计概率分布函数F(x)定义为:
F(x) = P(X ≤ x) = ΣP(X = x’)
其中,x’为所有小于或等于x的可能取值。
以连续随机变量为例,设随机变量X具有概率密度函数f(x),则其累计概率分布函数F(x)定义为:
F(x) = P(X ≤ x) = ∫f(t)dt,积分从负无穷到x
累计概率分布函数提供了随机变量小于或等于某个特定值的概率。在统计学和概率论中,累计概率分布函数常用于计算随机变量的分位数、概率计算以及随机变量之间的比较等任务。
值得注意的是,累计概率分布函数的取值范围在[0, 1]之间,并且具有单调递增的性质。
概率分布函数
概率分布函数(Probability Distribution Function,简称PDF)是描述随机变量取值与其概率之间关系的函数。对于离散型随机变量,概率分布函数也被称为概率质量函数(Probability Mass Function,简称PMF)。对于连续型随机变量,概率分布函数也被称为概率密度函数(Probability Density Function,简称PDF)。
离散型随机变量的概率质量函数(PMF):
对于离散型随机变量X,其概率质量函数P(X = x)给出了X取特定值x的概率。概率质量函数满足以下性质:
非负性:P(X = x) ≥ 0
归一性:∑P(X = x) = 1,求和范围覆盖了所有可能的取值
连续型随机变量的概率密度函数(PDF):
对于连续型随机变量X,其概率密度函数f(x)描述了X落在某个区间内的概率密度。概率密度函数满足以下性质:
非负性:f(x) ≥ 0
归一性:∫f(x)dx = 1,积分范围覆盖了所有可能的取值
概率分布函数是概率质量函数(PMF)或概率密度函数(PDF)的累积函数。对于离散型随机变量,概率分布函数F(x)定义为X小于或等于x的概率之和。对于连续型随机变量,概率分布函数F(x)定义为X小于或等于x的概率密度之积分。
概率分布函数的性质:
非负性:概率分布函数的值始终非负,即F(x) ≥ 0。
单调性:概率分布函数是单调非减函数,即如果x1 ≤ x2,则F(x1) ≤ F(x2)。
归一性:概率分布函数在整个取值空间上的值范围是[0, 1],即F(-∞) = 0,F(+∞) = 1。
概率分布函数在统计学和概率论中起到重要的作用,可以用于计算随机变量的概率、期望、方差以及进行随机变量之间的比较等任务。常见的概率分布函数包括正态分布、均匀分布、二项分布、泊松分布等。
度量空间
度量空间(Metric Space)是数学中的一个概念,用于描述具有度量(Metric)的空间。度量是一种用于衡量空间中两个元素之间距离的函数。
在一个度量空间中,我们有一个集合X以及一个定义在X上的度量函数d,满足以下条件:
非负性:对于任意的x, y ∈ X,有d(x, y) ≥ 0,并且当且仅当x = y时,d(x, y) = 0。
对称性:对于任意的x, y ∈ X,有d(x, y) = d(y, x)。
三角不等式:对于任意的x, y, z ∈ X,有d(x, z) ≤ d(x, y) + d(y, z)。
度量空间中的度量函数可以理解为表示元素之间距离的度量方式。它可以是实数值的距离,也可以是其他形式的度量,如欧氏距离、曼哈顿距离等。度量函数的定义使我们能够在度量空间中进行距离的比较和分析。
度量空间的例子包括欧几里得空间(Euclidean Space)和离散度量空间。在欧几里得空间中,度量函数是欧氏距离,用于测量点之间的直线距离。在离散度量空间中,度量函数可以是汉明距离、编辑距离等,用于度量离散对象之间的差异。
度量空间的概念在数学、计算机科学和物理学等领域中有广泛的应用。它为我们提供了一种形式化的框架,用于研究和分析空间中的距离、连续性、收敛性等性质。
负采样(Negative Sampling)
负采样(Negative Sampling,负样本的采样方式)是一种用于优化训练过程的技术,常用于词嵌入模型(如Word2Vec)等自然语言处理任务中。负采样通过减少训练样本的数量和计算复杂度,提高了训练效率,同时仍能保持模型的性能。
在传统的词嵌入模型中,目标是学习每个单词的词向量表示,使得具有相似上下文的单词在向量空间中的距离更近。传统的训练过程中,需要对每个训练样本计算softmax概率分布,这对于大规模语料库来说计算量很大。
负采样通过将训练样本中的正例(目标单词及其上下文)与负例(目标单词与随机选择的其他单词)进行区分,从而减少了计算量。具体来说,对于每个训练样本,负采样会随机选择一些负例,数量通常远小于语料库中的所有单词,并将它们作为负样本,而不再考虑其他单词。
负采样的目标是调整模型参数,使得正例的得分高于负例的得分,从而更好地区分正例和负例。一种常见的负采样方法是使用二元逻辑回归模型,将目标单词与上下文的词向量作为输入,通过sigmoid函数将其转化为概率。正例的标签为1,负例的标签为0,模型的目标是最大化正例的概率、最小化负例的概率。
负采样的优点是能够降低计算复杂度,加快训练速度。此外,负采样还有助于将模型更专注于区分目标单词和上下文,提高了模型的性能。但是,负采样也引入了一定的偏差,因为负例是随机选择的,并不能保证完全涵盖语料库中的所有负例。
需要注意的是,负采样在不同任务和模型中的具体实现方式会有所不同。具体的选择和调整负采样的数量、采样策略等,需要根据实际情况和任务需求进行调整和优化。
除了二元逻辑回归模型,还有其他几种常用的负采样方式,下面列举其中两种。
基于分布的负采样(Distribution-based Negative Sampling):
这种负采样方式基于单词的频率分布来选择负例。具体步骤如下:
统计每个单词在语料库中的出现频次,并计算每个单词出现的概率。
根据单词的概率分布,随机选择负例。常用的选择方法是使用单词的概率分布的幂次进行采样,即根据频次的幂次对单词进行采样,出现频次较高的单词被选择为负例的概率较低,频次较低的单词被选择为负例的概率较高。
基于近邻的负采样(Neighbor-based Negative Sampling):
这种负采样方式基于单词的上下文关系来选择负例。具体步骤如下:
对于每个训练样本中的目标单词,选取其真实上下文单词。
对于每个上下文单词,从其上下文窗口中选择一部分单词作为负例。这些负例单词可以是随机选择的,也可以根据一定的概率分布进行选择。
这些负采样方式的选择取决于具体的任务和模型。不同的负采样方式可能适用于不同的应用场景,并且可能会对模型的性能产生不同的影响。因此,在实际应用中,可以尝试不同的负采样方式,并进行实验和比较,选择最适合的方式。
相关文章:
累计概率分布、概率分布函数(概率质量函数、概率密度函数)、度量空间、负采样(Negative Sampling)
这里写自定义目录标题 机器学习的基础知识累计概率分布概率分布函数度量空间负采样(Negative Sampling)基于分布的负采样(Distribution-based Negative Sampling):基于近邻的负采样(Neighbor-based Negativ…...

〔001〕虚幻 UE5 安装教程
✨ 目录 🎈 下载启动程序🎈 注册个人账户🎈 选择引擎版本🎈 选择安装选项🎈 虚幻商城的使用🎈 每月免费插件🎈 安装插件🎈 下载启动程序 下载地址:https://www.unrealengine.com/zh-CN/download点击上面地址,下载 UE5 启动程序并安装🎈 注册个人账户 打开商…...

Crypto(8) BUUCTF-bbbbbbrsa1
题目描述: from base64 import b64encode as b32encode from gmpy2 import invert,gcd,iroot from Crypto.Util.number import * from binascii import a2b_hex,b2a_hex import randomflag "******************************"nbit 128p getPrime(nbit)…...
软件测试之随机测试详解
在软件测试中除了根据测试用例和测试说明书进行功能测试外,还需要进行随机测试,随机测试是没有书面测试用例、记录期望结果、检查列表、脚本或指令的测试。主要是根据测试者的经验对软件进行功能和性能抽查。随机测试是根据测试说明书执行测试用例的重要…...

【广州华锐互动】3D全景虚拟旅游在文旅行业的应用场景
随着科技的不断发展,3D全景虚拟旅游正在成为一种新兴的旅游体验方式,它可以帮助旅游者更加深入地了解旅游信息,提升旅游体验。下面我们将详细介绍3D全景虚拟旅游可以应用于哪些场景。 一、旅游规划 3D全景虚拟旅游可以帮助旅游者更加直观地进…...
多目标跟踪算法 实时检测 - opencv 深度学习 机器视觉 计算机竞赛
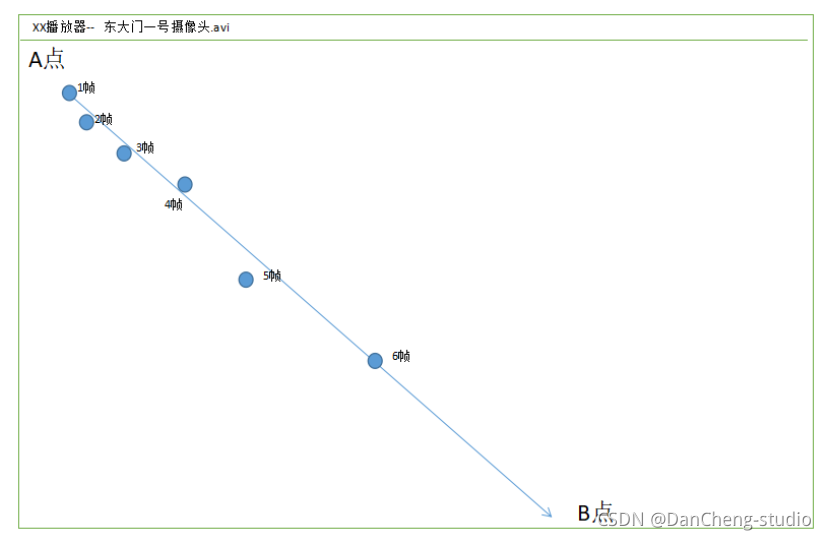
文章目录 0 前言2 先上成果3 多目标跟踪的两种方法3.1 方法13.2 方法2 4 Tracking By Detecting的跟踪过程4.1 存在的问题4.2 基于轨迹预测的跟踪方式 5 训练代码6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习多目标跟踪 …...

深入了解Jedis:Java操作Redis的常见类型数据存储
目录 前言 一、Jedis介绍 1.Jedis在各方面的功能 2.特点 二、Java连接Redis 1.导入pom依赖 2.建立连接 三、Java操作Redis的常见类型数据存储 1.字符串 2.哈希表 3.列表 4.集合 5.有序集合 四、Redis的实际应用场景实例 1.会议信息实体 2.自定义注解 3.创建切面…...

angular+ionic+npm项目运行
angularionicnpm项目运行 错误记录(1)Downloading binary from https://github.com/sass/node-sass/releases/download/v4.14.1/win32-x64-72_binding.node(2)The npm warning "A requires a peer of B but none is installe…...

【数据库】数据库模式 Schema
数据库模式 Schema 1.MySQL2.PostgreSQL3.SQL Server4.Oracle5.SQLite 在数据库的术语中,模式(schema)是一个逻辑概念,用于组织数据库中的对象。模式中的对象通常包括 表、索引、数据类型、序列、视图、存储过程、主键、外键 等等…...
RPC 原理详解
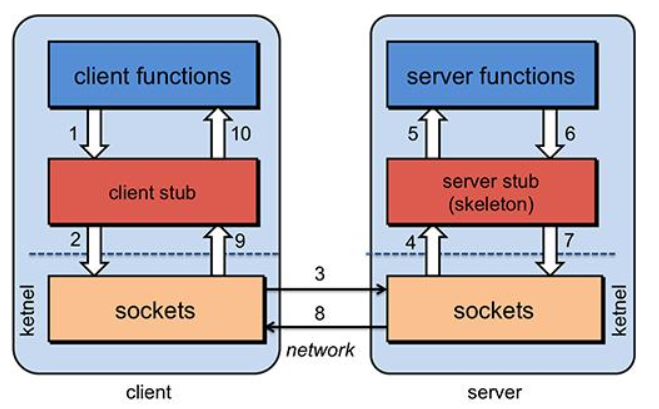
文章目录 什么是 RPCRPC 基本原理RPC核心功能服务寻址数据编解码网络传输一次RPC的调用过程 实践基于HTTP协议的RPC基于TCP协议的RPC 什么是 RPC RPC(Remote Procedure Call),即远程过程调用,它允许像调用本地服务一样调用远程服…...
新版Helix QAC 100%覆盖MISRA C++:2023
Helix QAC 2023.3预期将100%覆盖在2023年第四季度发布的新的MISRA C:2023规则。 此外,该版本支持更多的C20语言特性,并改进了Perforce Validate平台和Helix QAC与Validate的集成,以及其他质量改进。 编码标准覆盖率(MISRA C:202…...

maven 项目添加 git-hook 脚本,约束提交内容格式
git 提交代码,推送代码,可以通过在 .git/hooks 目录中的 bash 脚本来做一定的验证工作。 本例使用插件 maven-antrun-plugin 自动输出脚本至 .git/hooks 目录中,在 pom.xml 中的使用示例如下: <plugin><groupId>org.…...

18、Flink的SQL 支持的操作和语法
Flink 系列文章 1、Flink 部署、概念介绍、source、transformation、sink使用示例、四大基石介绍和示例等系列综合文章链接 13、Flink 的table api与sql的基本概念、通用api介绍及入门示例 14、Flink 的table api与sql之数据类型: 内置数据类型以及它们的属性 15、Flink 的ta…...

泛微OA_lang2sql 任意文件上传漏洞复现
简介 泛微OA E-mobile系统 lang2sql接口存在任意文件上传漏洞,由于后端源码中没有对文件没有校验,导致任意文件上传。攻击者可利用该参数构造恶意数据包进行上传漏洞攻击。 漏洞复现 FOFA语法: title"移动管理平台-企业管理" 页…...
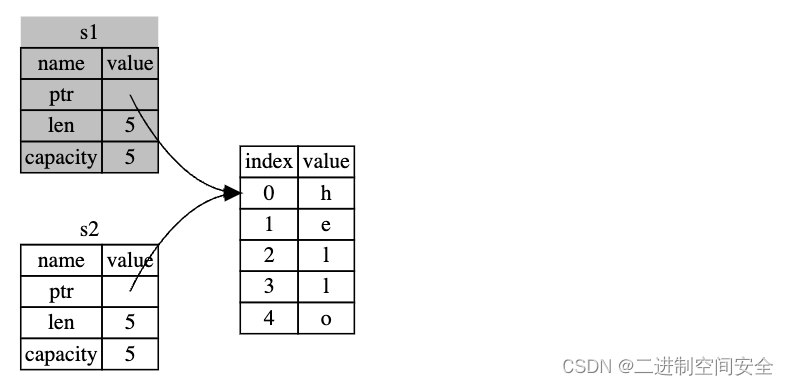
Rust编程基础核心之所有权(上)
1.什么是所有权? Rust 的核心功能(之一)是 所有权(ownership)。虽然该功能很容易解释,但它对语言的其他部分有着深刻的影响。 所有程序都必须管理其运行时使用计算机内存的方式。一些语言中具有垃圾回收机制&#x…...

优化改进YOLOv5算法之添加DCNv3模块,有效提升目标检测效果
目录 前言 1 DCNv3原理 1.1 DCNv2 1.2 DCNv3 1.3 模型架构 2 YOLOv5算法中加入DCNv3模块...

VSCode 连接不上 debian 的问题
之前一台笔记本上安装了 debian12,当时用 vscode 是可以连接上的,但今天连接突然就失败了,失败信息是这样的: 查看失败信息 因为 debian 是自动获取 ip 地址的,以前能连接上时,ip 地址是 104,然…...
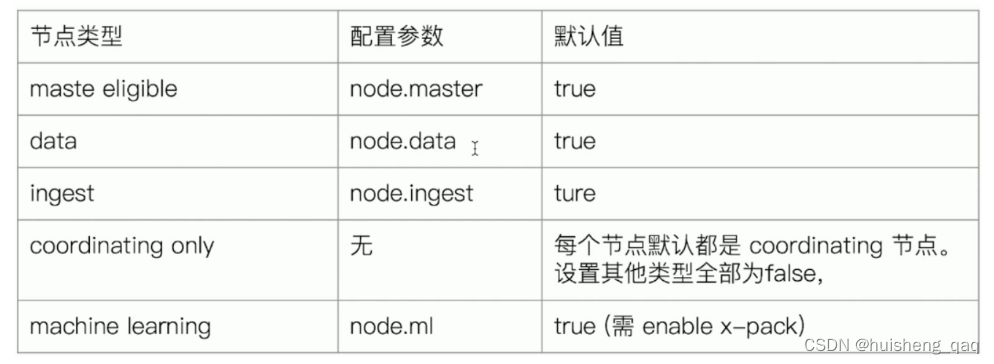
【ElasticSearch系列-06】Es集群架构的搭建以及集群的核心概念
ElasticSearch系列整体栏目 内容链接地址【一】ElasticSearch下载和安装https://zhenghuisheng.blog.csdn.net/article/details/129260827【二】ElasticSearch概念和基本操作https://blog.csdn.net/zhenghuishengq/article/details/134121631【三】ElasticSearch的高级查询Quer…...

软考高级系统架构设计师系列案例考点专题六:面向服务架构设计
软考高级系统架构设计师系列案例考点专题六:面向服务架构设计 一、面向服务架构设计内容大纲二、SOA概述和发展三、SOA和微服务的区别四、SOA的参考架构五、SOA主要协议和规范六、SOA设计标准和原则七、SOA设计模式八、SOA构建和实施一、面向服务架构设计内容大纲 SOA概述和发…...

【入门Flink】- 07Flink DataStream API【万字篇】
DataStream API 是 Flink 的核心层 API。一个 Flink 程序,其实就是对DataStream的各种转换。 代码基本上都由以下几部分构成: 执行环境(Execution Environment) 1)创建执行环境StreamExecutionEnvironment StreamExe…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
