吴恩达《机器学习》6-1->6-3:分类问题、假设陈述、决策界限
一、什么是分类问题?
在分类问题中,我们试图预测的变量𝑦是离散的值,通常表示某种类别或标签。这些类别可以是二元的,也可以是多元的。分类问题的示例包括:
- 判断一封电子邮件是否是垃圾邮件(二元分类)
- 判断一次金融交易是否涉及欺诈(二元分类)
- 区分肿瘤是恶性的还是良性的(二元分类)
- 图像识别:将图像分为不同的类别(多元分类)
分类问题在现实世界中无处不在,因此开发有效的分类算法至关重要。逻辑回归是其中一种应用最广泛的分类算法。

二、逻辑回归
逻辑回归是一种分类算法,尽管其名称中包含“回归”,但它实际上是用于分类任务的算法。逻辑回归的特点是其输出值永远在0到1之间,这使得它非常适合处理离散的标签,如0和1。
与线性回归不同,逻辑回归的输出范围被约束在[0, 1]之间,因此它适用于计算概率。具体来说,逻辑回归模型使用一个逻辑函数(Sigmoid函数)来将输入映射到0和1之间。逻辑函数的公式为:
g(z) = 1 / (1 + e^(-z))在这个公式中,z表示输入,g(z)表示逻辑函数。逻辑函数的作用是计算在给定输入条件下,输出为1的可能性。如果g(z)大于等于0.5,则模型预测为1;如果g(z)小于0.5,则模型预测为0。

三、假设函数表示
逻辑回归模型的假设函数表示如下:
ℎ𝜃(𝑥) = 𝑔(𝜃^𝑇𝑥)在这个表示中,𝑥代表特征向量,𝑔代表逻辑函数。模型的任务是根据选择的参数计算输出变量为1的可能性,即ℎ𝜃(𝑥) = 𝑃(𝑦 = 1|𝑥; 𝜃)。例如,如果计算得到ℎ𝜃(𝑥) = 0.7,那么表示有70%的几率𝑦为正向类,相应地𝑦为负向类的几率为0.3。

四、判定边界
在逻辑回归中,我们通过选择适当的参数𝜃来定义一个决策边界(decision boundary),该边界将数据分为不同的类别。决策边界是一个分割区域,对于不同的输入数据,模型会预测其属于不同的类别。
逻辑回归的假设函数可以表示为:
ℎ𝜃(𝑥) = 𝑔(𝜃0 + 𝜃1𝑥1 + 𝜃2𝑥2 + 𝜃3𝑥1² + 𝜃4𝑥2²)在上述表达式中,𝑥1和𝑥2是特征,𝜃0、𝜃1、𝜃2、𝜃3、𝜃4是模型的参数。根据不同的参数,我们可以得到不同的决策边界。这意味着逻辑回归模型可以适应各种形状的决策边界,从简单的直线到复杂的曲线。

参考资料:
[中英字幕]吴恩达机器学习系列课程
黄海广博士 - 吴恩达机器学习个人笔记
相关文章:

吴恩达《机器学习》6-1->6-3:分类问题、假设陈述、决策界限
一、什么是分类问题? 在分类问题中,我们试图预测的变量𝑦是离散的值,通常表示某种类别或标签。这些类别可以是二元的,也可以是多元的。分类问题的示例包括: 判断一封电子邮件是否是垃圾邮件(二…...
C语言 用字符串比较函数cmp来做一个门禁:账号密码是否匹配 (干货满满)
#include<stdio.h> #include<string.h> void fun04() {for (int i 0; i < 3; i){char *str01 "hello";char uname[100] ;printf("请输入账号");scanf("%s",uname);char *str02 "123456";char pword[100];printf(&qu…...
Uniapp实现多语言切换
前言 之前做项目过程中,也做过一次多语言切换,大致思想都是一样的,想了解的可以看下之前的文章C#WinForm实现多语言切换 使用i18n插件 安装插件 npm install vue-i18n --saveMain.js配置 // 引入 多语言包 import VueI18n from vue-i18n…...
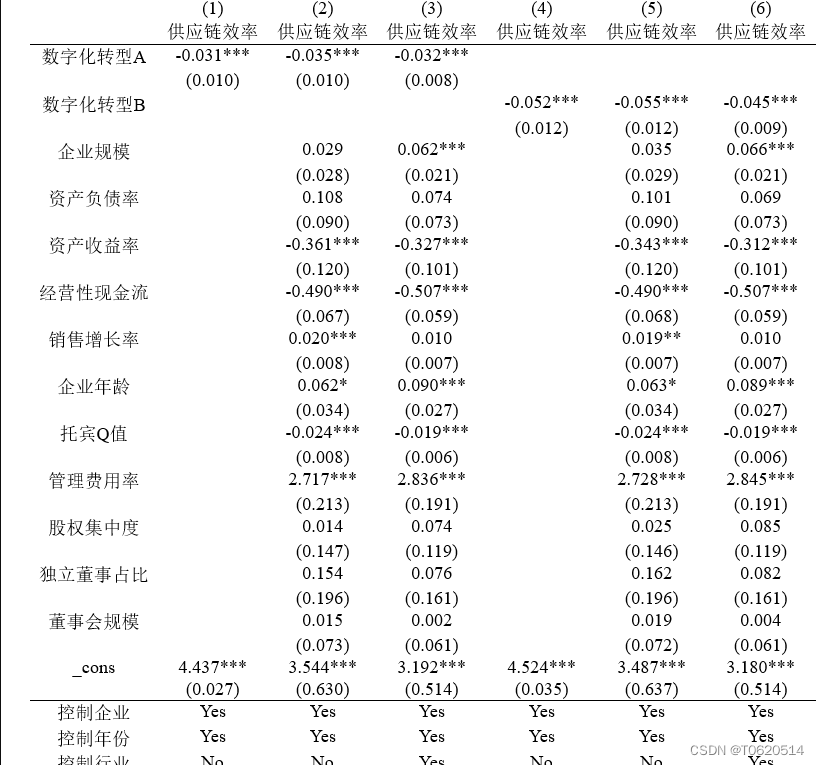
企业数字化转型与供应链效率-基准回归复刻(2007-2022年)
参照张树山(2023)的做法,本团队对来自统计与决策《企业数字化转型与供应链效率》一文中的基准回归部分进行复刻。文章实证检验企业数字化转型对供应链效率的影响。用年报词频衡量上市公司数字化转型程度,以库存周转天数来衡量供应…...
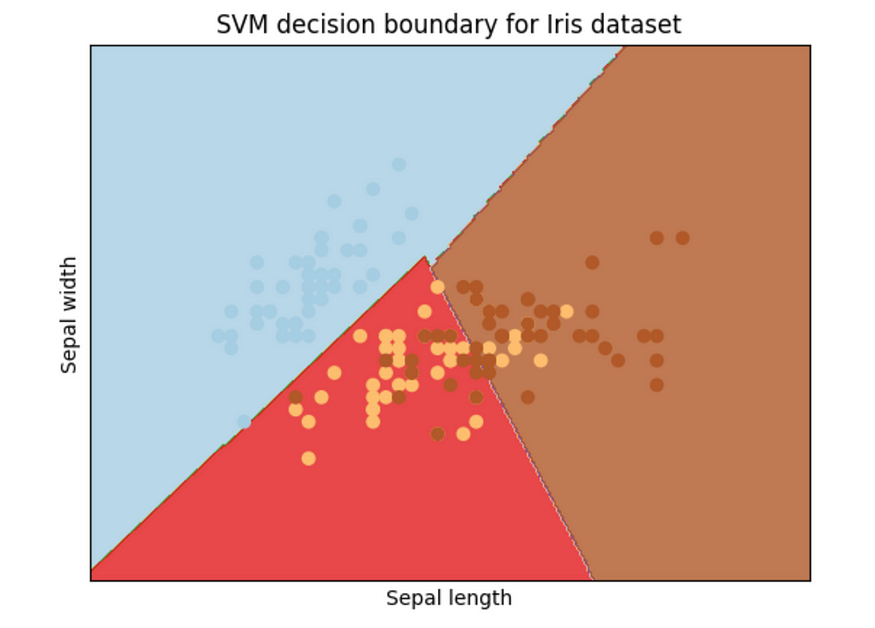
支持向量机 (SVM):初学者指南
照片由 Unsplash上的 vackground.com提供 一、说明 SVM(支持向量机)简单而优雅用于分类和回归的监督机器学习方法。该算法试图找到一个超平面,将数据分为不同的类,并具有尽可能最大的边距。本篇我们将介绍如果最大边距不存在的时候…...
UnityShader(五)
这次要用表面着色器实现一个水的特效。先翻到最下边看代码,看不懂再看下面的解释。 首先第一步要实现水的深浅判断,实现深水区和浅水区的区分。 这里需要用到深度图的概念。不去说太多概念,只去说怎么实现的,首先我们的水面是在…...
Java中的类和对象
文章目录 一、类和对象的基本概念二、类和对象的定义和使用1.创建类的语法2.创建类的对象3.范例(创建一个类的对象) 三、this引用1.什么是this引用2.this引用的特性 四、构造方法五、封装1.封装的概念2.访问限定符3.封装扩展包3.1包的概念3.2常见的包 六、static成员1.static修…...

多测师肖sir_高级金牌讲师_jenkins搭建
jenkins操作手册 一、jenkins介绍 1、持续集成(CI) Continuous integration 持续集成 团队开发成员每天都有集成他们的工作,通过每个成员每天至少集成一次,也就意味着一天有可 能多次集成。在工作中我们引入持续集成,通…...

Ps:色彩范围
Ps菜单:选择/色彩范围 Select/Color Range 色彩范围 Color Range是一个功能强大选择命令,不仅可以基于颜色进行选择,而且可以基于影调进行选择。不仅可以用来检测人脸选择肤色,也可用来选择超出印刷色域范围的区域。 在图层蒙版的…...
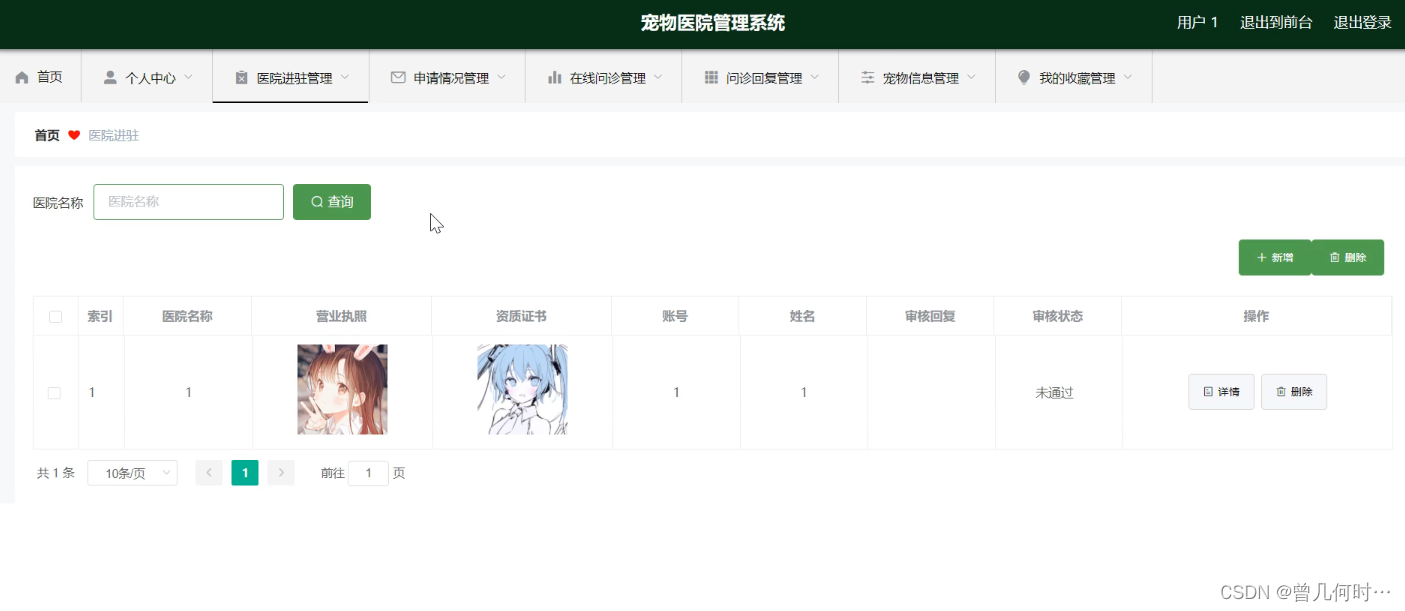
基于SSM的宠物医院管理系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

华为政企园区网络交换机产品集
产品类型产品型号产品说明 核心/汇聚交换机CloudEngine S5731-H24P4XCCloudEngine S5731-H24P4XC 提供 24个10/100/1000BASE-T以太网端口,4个万兆SFP,CloudEngine S5731-H 系列交换机是华为公司推出的新一代智能千兆交换机,基于华为公司统…...

NVMe FDP会被广泛使用吗?
文章开头,我们需要先了解固态硬盘的读写机制。我们知道,固态硬盘的存储单元是由闪存颗粒组成的,无法实现物理性的数据覆盖,只能擦除然后写入,重复这一过程。因而,我们可以想象得到,在实际读写过…...
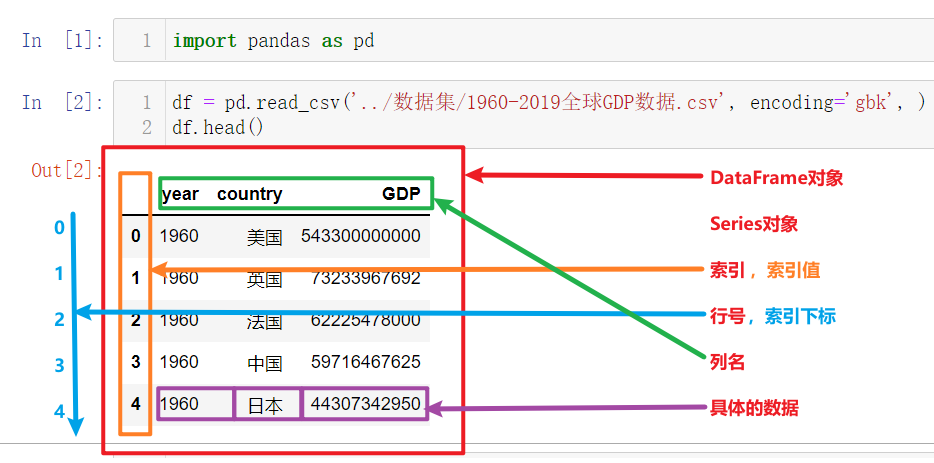
[黑马程序员Pandas教程]——Pandas数据结构
目录: 学习目标认识Pandas中的数据结构和数据类型Series对象通过numpy.ndarray数组来创建通过list列表来创建使用字典或元组创建s对象在notebook中不写printSeries对象常用API布尔值列表获取Series对象中部分数据Series对象的运算DataFrame对象创建df对象DataFrame…...

AI 绘画 | Stable Diffusion 提示词
Prompts提示词简介 在Stable Diffusion中,Prompts是控制模型生成图像的关键输入参数。它们是一种文本提示,告诉模型应该生成什么样的图像。 Prompts可以是任何文本输入,包括描述图像的文本,如“一只橘色的短毛猫,坐在…...

tomcat默认最大线程数、等待队列长度、连接超时时间
tomcat默认最大线程数、等待队列长度、连接超时时间 tomcat的默认最大线程数是200,默认核心线程数(最小空闲线程数)是10。 在核心线程数满了之后,会直接启用最大线程数(和JDK线程池不一样,JDK线程池先使用工作队列再使用最大线程…...

本地部署 CogVLM
本地部署 CogVLM CogVLM 是什么CogVLM Github 地址部署 CogVLM启动 CogVLM CogVLM 是什么 CogVLM 是一个强大的开源视觉语言模型(VLM)。CogVLM-17B 拥有 100 亿视觉参数和 70 亿语言参数。 CogVLM-17B 在 10 个经典跨模态基准测试上取得了 SOTA 性能&am…...
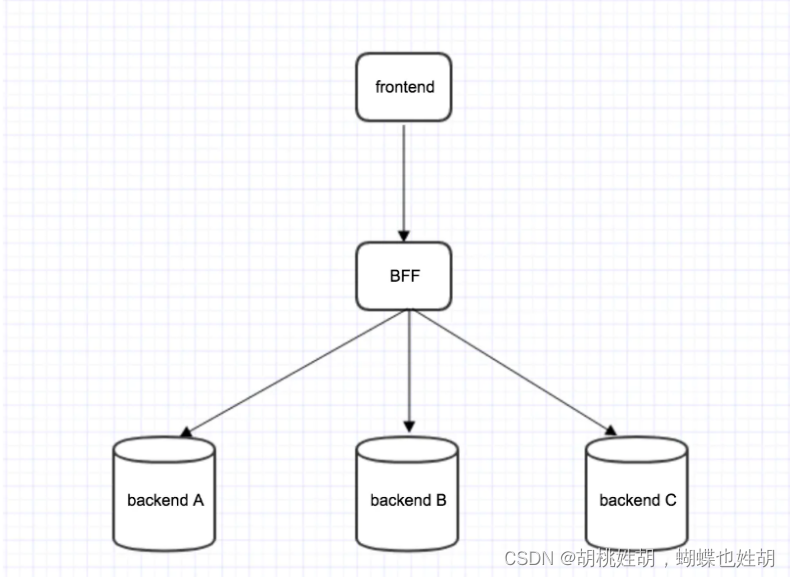
bff层解决了什么痛点
bff层 -- 服务于前端的后端 什么是bff? Backend For Frontend(服务于前端的后端),也就是服务器设计API的时候会考虑前端的使用,并在服务端直接进行业务逻辑的处理,又称为用户体验适配器。BFF只是一种逻辑…...

面试经典150题——Day33
文章目录 一、题目二、题解 一、题目 76. Minimum Window Substring Given two strings s and t of lengths m and n respectively, return the minimum window substring of s such that every character in t (including duplicates) is included in the window. If there …...
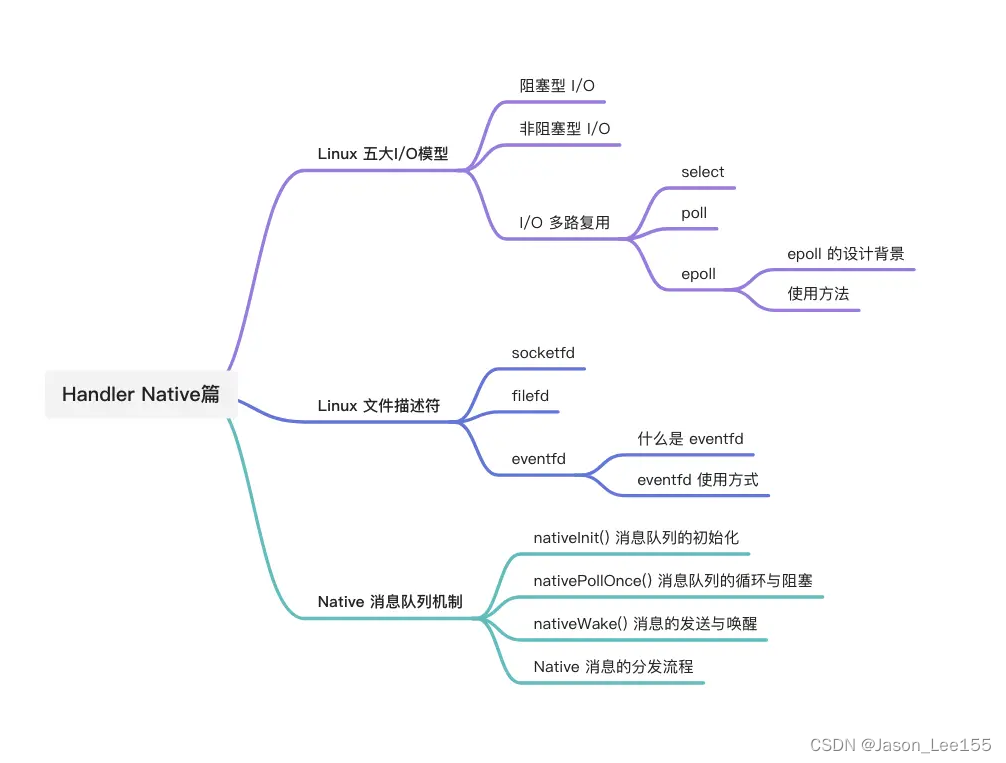
再谈Android重要组件——Handler(Native篇)
前言 最近工作比较忙,没怎么记录东西了。Android的Handler重要性不必赘述,之前也写过几篇关于hanlder的文章了: Handler有多深?连环二十七问Android多线程:深入分析 Handler机制源码(二) And…...
Javaweb之javascript的详细解析
JavaScript html完成了架子,css做了美化,但是网页是死的,我们需要给他注入灵魂,所以接下来我们需要学习JavaScript,这门语言会让我们的页面能够和用户进行交互。 1.1 介绍 通过代码/js效果演示提供资料进行效果演示&…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
