地理信息系统原理-空间数据结构(7)
四叉树编码
1.四叉树编码定义
四叉树数据结构是一种对栅格数据的压缩编码方法,其基本思想是将一幅栅格数据层或图像等分为四部分,逐块检查其格网属性值(或灰度);如果某个子区的所有格网值都具有相同的值,则这个子区就不再分割,否则还要把这个子区再分割成四个子区,这样依次地分割,直到每个子块都只含有相同的属性值或灰度值为止,可分为自上而下编码和自下而上编码
2.四叉树表示形式
用一倒立树表示这种分割和分割结果,如图所示。
根:整个区域
高:深度、分几级,几次分割
叶:不能再分割的块
结点(或树叉):还需分割的块
每个树叉均有4个分叉,叫四叉树。

3.四叉树的分类
四叉树分为常规四叉树和线性四叉树
(1) 常规四叉树(记录这棵树的叶结点外,中间结点,结点之间的联系用指针联系,每个结点需要6个变量:父结点指针、四个子结点的指针和本结点的属性值。)
指针不仅增加了数据的存储量,还增加了操作的复杂性:如层次数(分割次数)由从父结点移到根结点的次数来确定,结点所代表的图像块的位置需要从根节点开始逐步推算下来。所以,常规四叉树并不广泛用于存储数据,主要在数据索引和图幅索引等方面应用
(2)线性四叉树则只存贮最后叶结点的信息,包括叶结点的位置编码/地址码、属性或灰度值;线性四叉树地址码,通常采用十进制Morton码(MD码):如图所示
①下图为一个8*8原始栅格数据

②依据自下而上的编码方式进行莫顿码编码
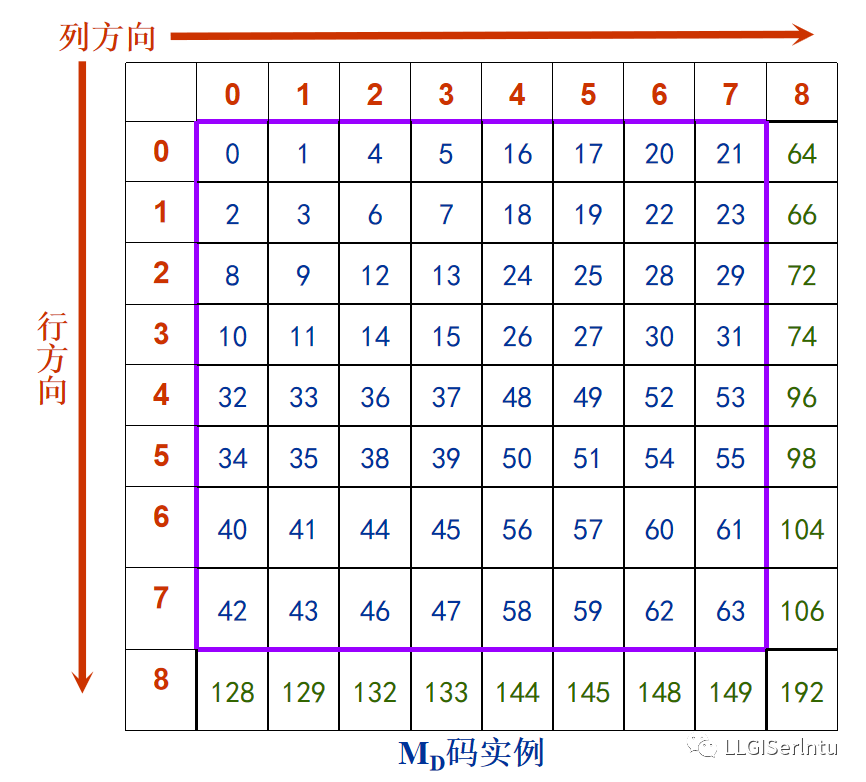
③在存储时,只存储属性值发生改变位置的莫顿码,就是叶节点的属性值

④如何计算莫顿码:如图所示,通常是将栅格数据十进制的行列号,转成二进制的行列号,再将二进制的行号和列号进行错位交叉排列,得到二进制的莫顿码,再将二进制的莫顿码转成十进制的莫顿码

4.四叉树编码特征
优点:
1)存贮量小,只对叶结点编码,节省了大量中间结点的存储,地址码隐含着结点的分割路径和分割次数。对于团块图像,四叉树表示法占用空间比上述其他方法要少得多,四叉树表示法基本上是一种非冗余表示法。
2)线性四叉树可直接寻址,通过其坐标值直接计算其Morton码,而不用建立四叉树(自下而上)。
3) 容易执行实现集合相加等组合操作
4)四叉树具有可变率或多重分辩率的特点使得它有很好的应用前景,适用于处理凝聚性或呈块状分布的空间数据,特别适用于处理分布不均匀的块状空间数据,但不适用于连续表面(如地形)或线状地物。
缺点
1)四叉树未能直接表示物体间的拓扑关系。
2) 与非树表示法比较,四叉树表示法的缺点在于转换的不稳定性或叫滑动变异
例如,两个图像的差异仅由于平移,就会构成极为不同的四叉树,因而很难根据四叉树来判断这两个图像是否全同,故不利于做形状分析和模式识别,
3) 一个物体的图像在构成四叉树时会被分割到若干个象限中,使它失去了内在的相关性。
4)矢/栅正反变换还不理想。
5) 建立四叉树耗费机时很多。
6) 四叉树虽可修改,但很费事
相关文章:

地理信息系统原理-空间数据结构(7)
四叉树编码 1.四叉树编码定义 四叉树数据结构是一种对栅格数据的压缩编码方法,其基本思想是将一幅栅格数据层或图像等分为四部分,逐块检查其格网属性值(或灰度);如果某个子区的所有格网值都具有相同的值࿰…...
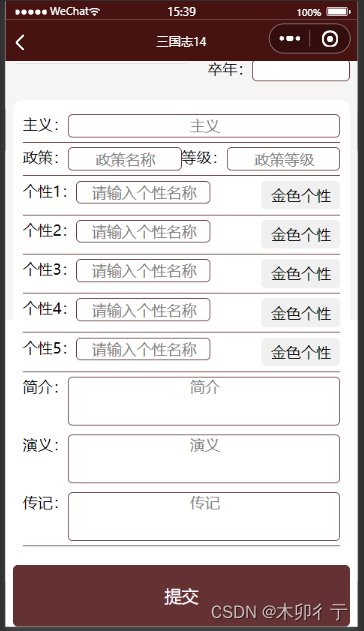
三国志14信息查询小程序(历史武将信息一览)制作更新过程03-主要页面的设计
1,小程序的默认显示 分为三部分,头部的标题、中间的内容区和底部的标签栏。点击标签可以切换不同页面,这是在app.json文件中配置的。代码如下: //所有用到的页面都需要在 pages 数组中列出,否则小程序可能会出现错误或…...
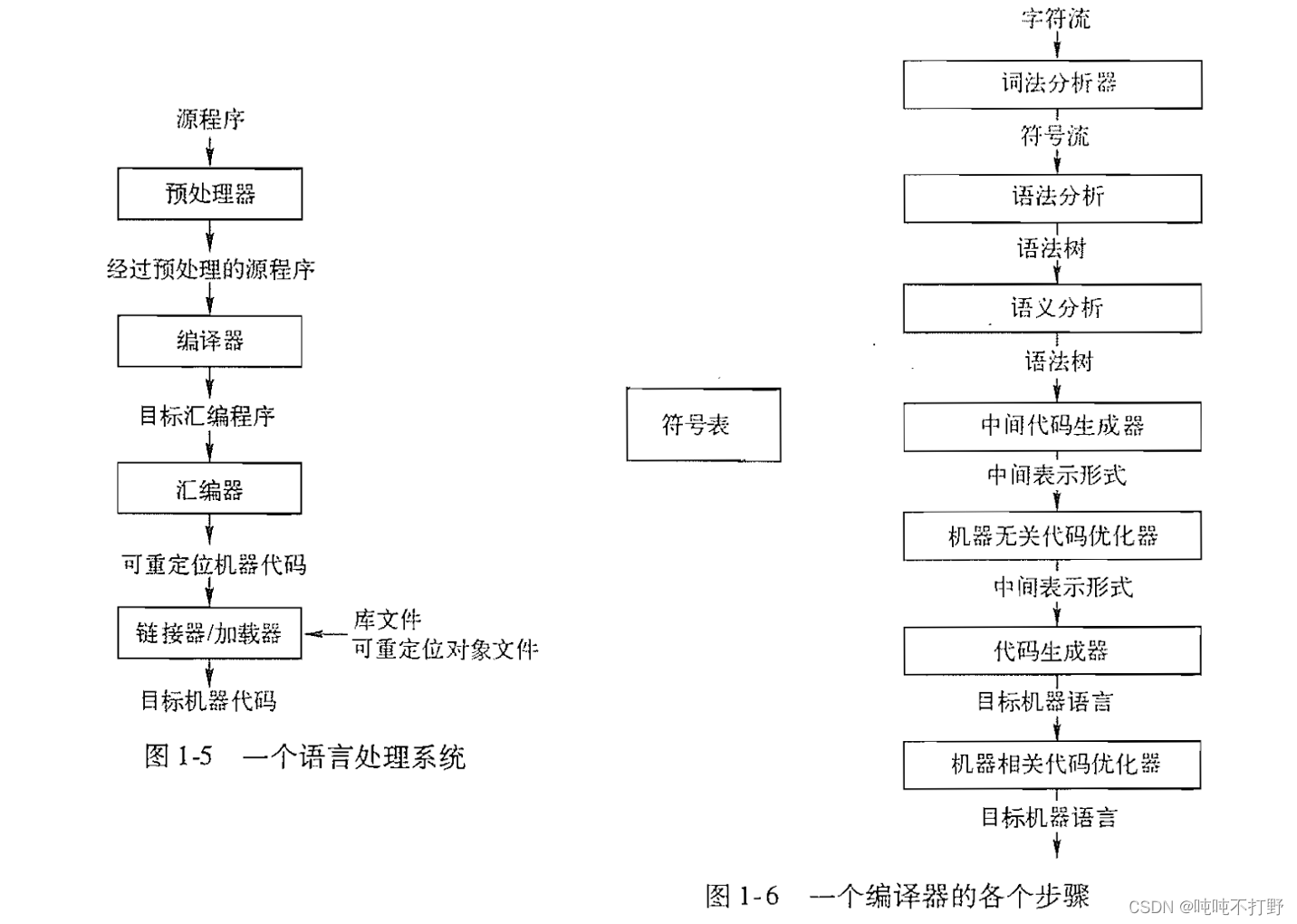
学习Opencv(蝴蝶书/C++)相关——2.用clang++或g++命令行编译程序
文章目录 1. c/cpp程序的执行1.1 cpp程序的编译过程1.2 预处理指令1.3 编译过程的细节2. macOS下使用Clang看cpp程序的编译过程2.1 示例2.1.1 第一步 预处理器-preprocessor2.1.2 第二步 编译器-compiler2.1.3 第三步 汇编器-assembler2.1.4 第四步 链接器-linker2.1.5 链接其他…...
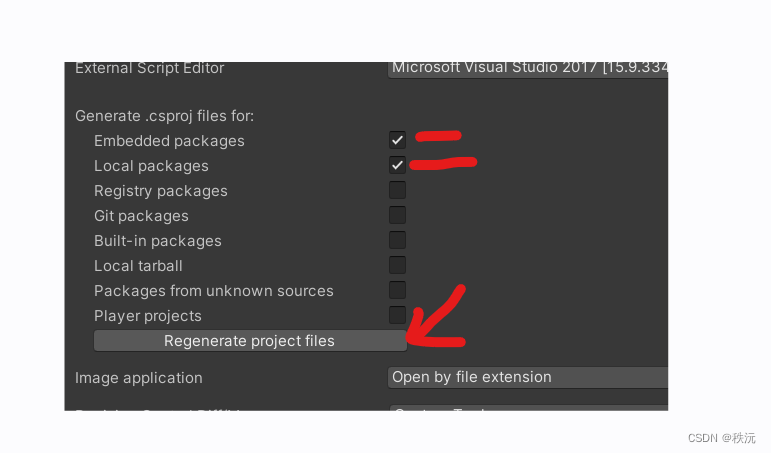
【Unity细节】VS不能附加到Unity程序中解决方法大全
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 😶🌫️收录于专栏:unity细节和bug 😶🌫️优质专栏 ⭐【…...

线上 kafka rebalance 解决
上周末我们服务上线完毕之后发生了一个kafka相关的异常,线上的kafka频繁的rebalance,详细的报错我已经贴到下面,根据字面意思:消费者异常 org.apache.kafka.clients.consumer.CommitFailedException: 无法完成提交,因为…...
)
[100天算法】-第一个错误的版本(day 62)
题目描述 你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。假设你有 n 个版本 [1, 2, ..., n],你…...

React 学习系列: 类组件生命周期方法
类组件生命周期方法 constructor 在类组件挂载的时候调用,用于构建一个类组件实例。 在构建类组件实例的时候, 会先执行基类构造函数( React.Component ) 使用父组件传入的 props 来初始化 props 属性, 然后执行自定义构造函数来初始化 state…...
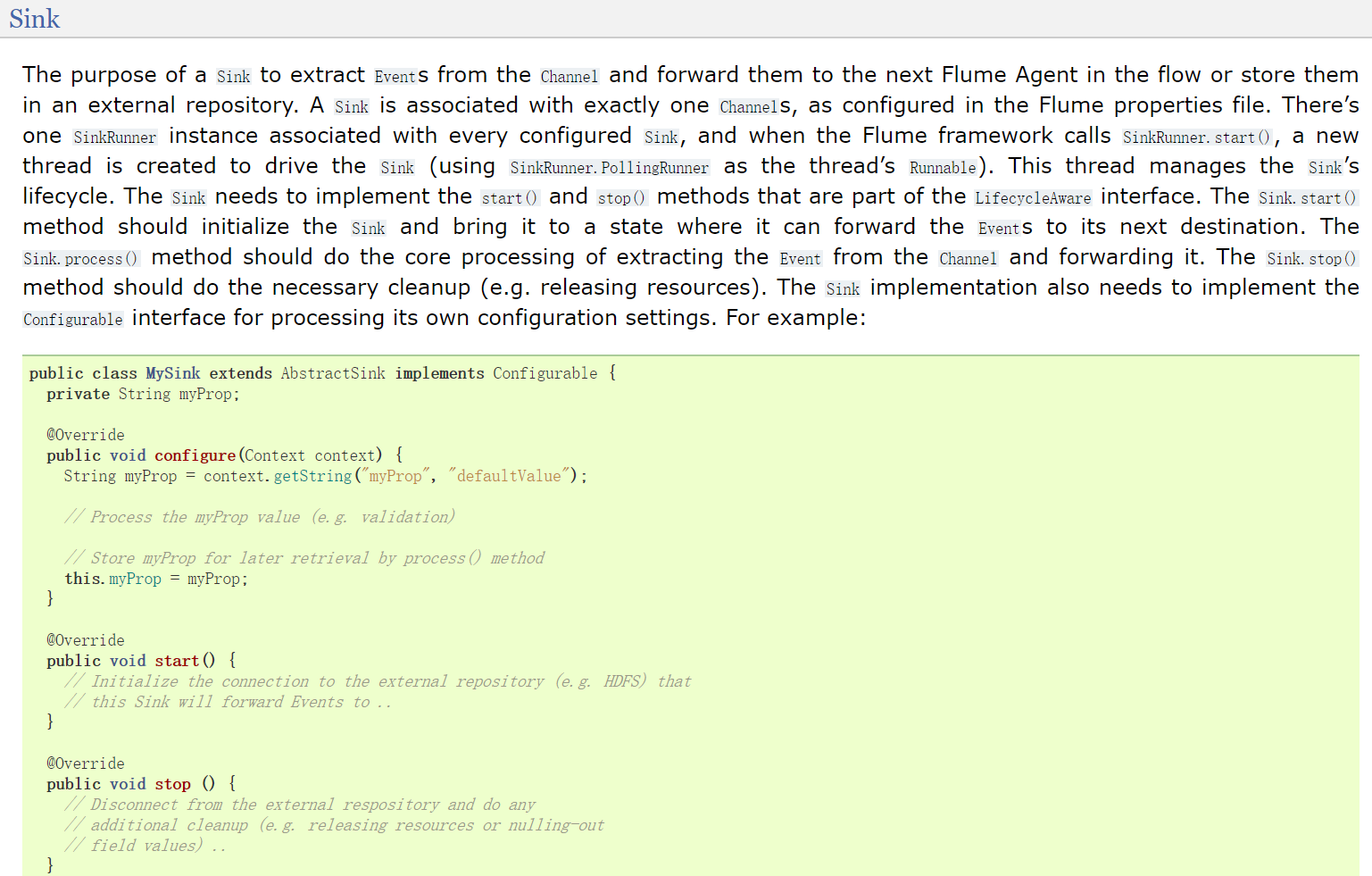
Flume从入门到精通一站式学习笔记
文章目录 什么是FlumeFlume的特性Flume高级应用场景Flume的三大核心组件Source:数据源channelsink Flume安装部署Flume的使用案例:采集文件内容上传至HDFS案例:采集网站日志上传至HDFS 各种自定义组件例如:自定义source例如&#…...
Python150题day08
2.基础语法篇 2.1 if 条件句 ①单个条件分支 使用input函数接收用户的输入,如果用户输入的整数是偶数,则使用print函数输出"你输入的整数是:{value],它是偶数”,[value]部分要替换成用户的输入。 解答: value input("请输⼊⼀…...

正则表达式的修饰符
正则表达式的修饰符是用来修改和调整正则表达式的特殊字符或元字符。修饰符可以改变正则表达式的行为和匹配方式。以下是一些常见的正则表达式修饰符: g(全局):表示全局匹配,即在整个字符串中搜索所有匹配项ÿ…...
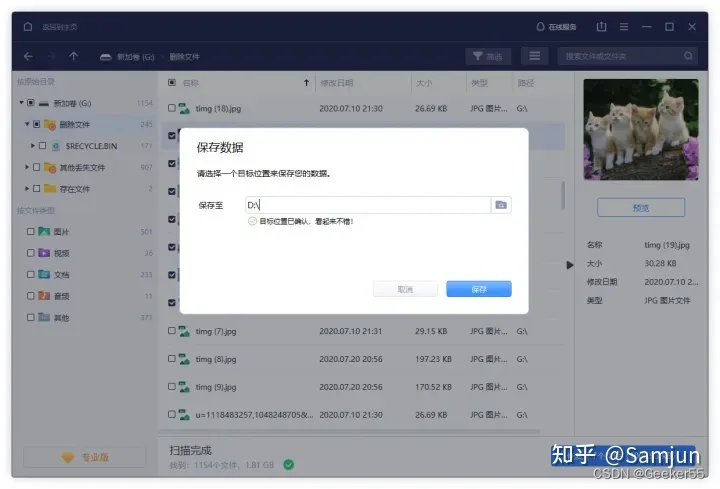
从行车记录仪恢复已删除/丢失视频的方法
“我的车里有行车记录仪。几天前,当我下班回家时,一辆卡车不知从哪里冒出来撞向了我。我们的两辆车都损坏了,但幸运的是,没有人受伤。我曾与卡车司机就修理我的汽车进行过会面,但他说我有错。我需要查看我的行车记录仪…...

TypeScript_抓取酒店价格数据
我们导入所需的库,包括http和request。然后,我们定义一个函数,该函数接受一个URL作为参数。 import http from http; import request from request;const fetchHotelPrices (url: string) > {// ... }接下来,我们使用request…...
vue前端实现多个url下载并合并为zip文件
一、安装 npm install jszip npm install file-saver 二、引入 import axios from axios import JSZip from "jszip"; import FileSaver from "file-saver"; 三、核心代码 videoData:[/video/26519f026fc012521605563015227403.mp4,/video/f7b9cdae14…...
Redis02-持久化策略
目录 RDB(Redis DataBase Backup file) RDB执行原理 AOF(Append-Only File) RDB和AOF对比 Redis支持多种持久化方式,以确保数据在内存中持久存储,以便在Redis服务器重启时数据不会丢失。Redis中持久化的…...
Crypto(9)[MRCTF2020]keyboard
下载题目,看看里面是什么 这是什么鬼,由题目可以获得线索,keyboard,不是键盘吗,然后看了看别人写的wp,发现是九键,有几个数字对应的密文就是第几个字母 比如第一个6,对应的字母是mno,…...

IOS自带的OCR识别功能
一、识别身份证 interface IDCardScanViewController () <AVCaptureMetadataOutputObjectsDelegate> property (nonatomic, strong) AVCaptureSession *captureSession; end implementation IDCardScanViewController - (void)viewDidLoad { [super viewDidLoad…...

1300*C. Product of Three Numbers(质数数学)
Problem - 1294C - Codeforces 解析: 首先这个数肯定不是质数,然后找到第一个因子p,对于n/p再判断质数,然后找到另外两个因子即可。 注意三个因子不能相同。 #include<bits/stdc.h> using namespace std; #define int long…...
【网络】五中IO模型介绍 + 多路转接中select和poll服务器的简单编写
高级IO 前言正式开始前面的IO函数简单过一遍什么叫做低效的IO钓鱼的例子同步IO和异步IO五种IO模型阻塞IO非阻塞IO信号驱动多路转接异步IO 小结 代码演示非阻塞IO多路转接select介绍简易select服务器timeout 为 nullptrtimeout 为 {0, 0}timeout 为 {5, 0}调用accept select编写…...

Camtasia2024破解版电脑屏幕录制剪辑软件
屏幕录制剪辑 TechSmith Camtasia for Mac v2021是 TechSmith 公司所开发出一款专业屏幕录像和编辑, Camtasia Studio2024版是由TechSmith公司官方进行汉化推出的最新版本,除2023版以下版本均没有官方汉化。 同时TechSmith公司打击第三方贩卖Camtasia Studio汉化的…...
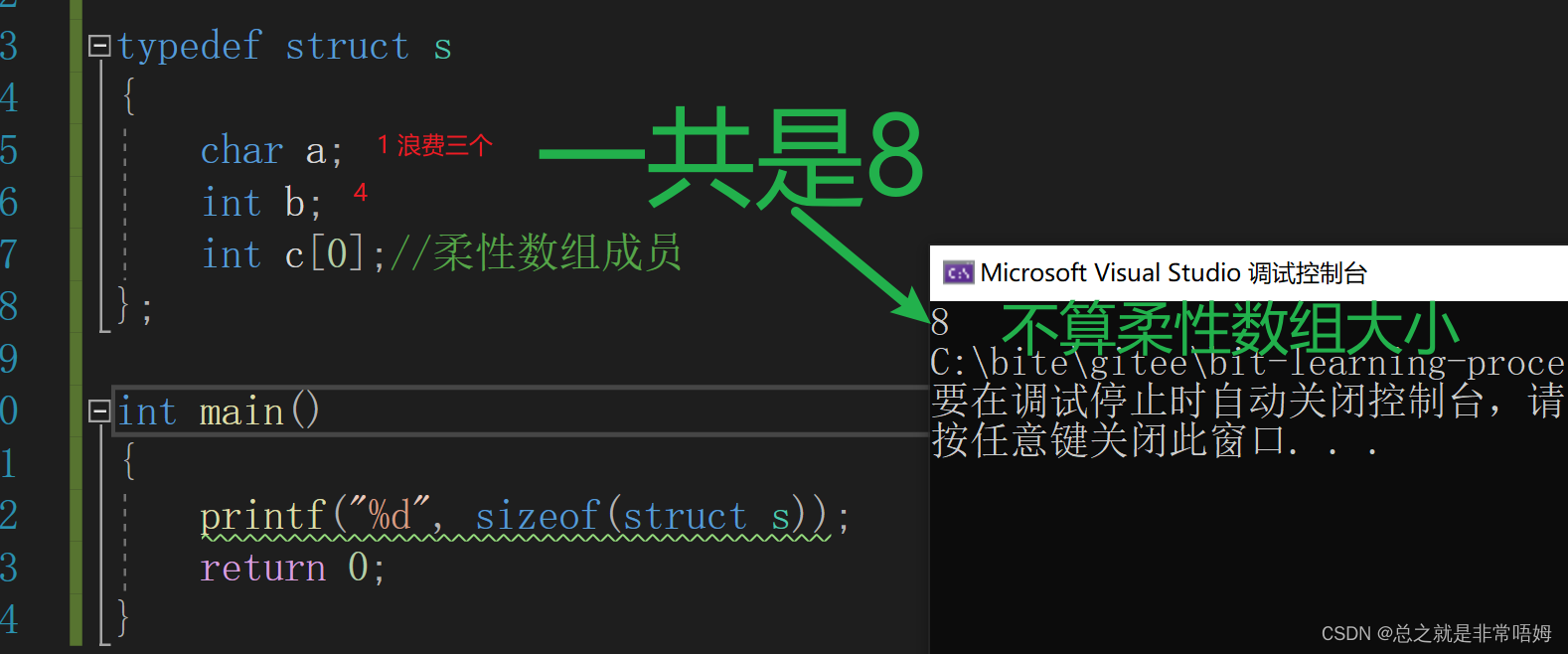
c语言进阶部分详解(《高质量C-C++编程》经典例题讲解及柔性数组)
上篇文章我介绍了介绍动态内存管理 的相关内容:c语言进阶部分详解(详细解析动态内存管理)-CSDN博客 各种源码大家可以去我的github主页进行查找:唔姆/比特学习过程2 (gitee.com) 今天便接“上回书所言”,来介绍《高质…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
