2021年03月 Python(四级)真题解析#中国电子学会#全国青少年软件编程等级考试

Python等级考试(1~6级)全部真题・点这里
一、单选题(共25题,每题2分,共50分)
第1题
不超过100个元素的有序数列,使用二分查找能找到指定的元素,可能的查找次数不包括?
A:1次
B:6次
C:7次
D:8次
答案:D
按照二分查找法的规律,100个元素的有序列表,不管是否找到,至多查找7次。
第2题
运行以下代码,正确的打印结果是?( )
def f():c=0for i in range(4,51,4):if i%6==0:c=c+1return cprint(f())
A:1
B:2
C:4
D:8
答案:C
函数f()的作用是求4-50间4和6的公倍数个数,即12的倍数个数。
第3题
10个人站一列,分苹果,问第10个人分到多少个苹果,他说比前面一个人多分到2个,依次往前,都说比前面一个人多分到2个,最后问第一个人,他说分到10个苹果。用以下函数求第10个人分到的苹果数,则应补充选项为?( )
def apple(n):if n == 1:return 10else:return print(apple(10))
A:apple(n)+2
B:n+2
C:apple(n-1)+2
D:apple(n+1)-2
答案:C
第4题
观察程序段,以下说法错误的是?( )
def fib(n):if n==1 or n==2:s=1else:s=fib(n-1)+fib(n-2)return sm=int(input("请输入m的值(m>2):"))print(fib(m))
A:如果输入m的值为8,打印的结果为20
B:该程序段用了递归来实现
C:如果缺少语句“return s”,程序会报错
D:语句“def fib(n):”中的n为形参
答案:A
定义函数时的语法如下:
def 函数名(参数集合):
<函数体>
[return 函数值]
本题中的自定义函数fib(m)需要返回值,所以“return 函数值”语句不能少,定义时“函数名<参数集合>”中的参数为形参,调用时“函数名<参数集合>” 中的参数为实参。如果输入m的值为8,打印的结果为21。
第5题
关于python函数参数的说法正确的是?
A:函数一定要有参数和返回值
B:在调用一个函数时,若函数中修改了形参变量的值,则对应的实参变量的值也被修改
C:参数的值是否会改变,与函数中对变量的操作有关,与参数类型无关
D:函数的形参在函数被调用时获得初始值
答案:D
函数的形参作用域为本函数,在函数被调用时获得初始值。
第6题
关于递归与递推方法的比较,错误的观点是?
A:递归是将复杂问题降解成若干个子问题,依次降解,求出低阶规模的解,代入高阶问题中,直至求出原问题的解;
B:递推是构造低阶的问题,并求出解,依次推导出高阶的问题以及解,直至求出问题的解;
C:数学上的递推关系可以通过递归的方法来实现;
D:递归算法代码简洁,运行速度比递推快,因此应该尽量采用递归的方法;
答案:D
D.递归的运行开销大。
第7题
运行以下代码,输出结果正确的是?( )
a=1b=c=[]def fun(a,c):a=2c.append(a)fun(a,c)print(a,b,c)
A:2 [2] [2]
B:1 [] [2]
C:1 [2] [2]
D:2 [] [2]
答案:C
函数体内变量a的值为2,添加到了列表c中,b和c指向同一个列表地址,因此列表b也随之改变
第8题
关于Turtle库的表述中,错误的是?
A:Turtle库是Python语言中一个很流行的绘制图像的函数库。
B:画布就是turtle为我们展开用于绘图区域,我们可以设置它的大小和初始位置。
C:turtle.circle( )是只能画一个指定半径为r的圆。
D:turtle.speed(speed):设置画笔移动速度,画笔绘制的速度范围[0,10]整数,数字越大越快。
答案:C
turtle.circle( )是turtle中的常用命令,基本语法是circle(radius,e),即画一个指定半径为r,角度e的圆或弧
第9题
有100枚金币,其中有1枚轻1克的假金币,现在要找出这枚假金币,但身边只有1个没有刻度的天秤。小明先是将金币分成50枚一堆,共两堆称重,在轻的那一堆中又分成两堆,接着在轻的25枚中分成12,12,1三堆称重,若两堆12枚的重量相同,则假币为单独剩下的那一枚,否则在轻的那一堆中继续按照之前的办法称下去,直到找到假金币。请问小明采用的办法与哪个算法有着相似之处?
A:递归
B:分治
C:枚举
D:贪心
答案:B
分治算法就是对一个问题采取各个击破的方法,将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。只要求出子问题的解,就可得到原问题的解。
第10题
运行以下代码,正确的打印结果是?( )
def f(s):t=0max=0for i in s:if i>="0" and i<="9":t=t+1else:if t>max:max=tt=0print(max)list="123ab45cd6d"f(list)
A:0
B:1
C:2
D:3
答案:D
本段代码中,函数f()的作用是求最长的连续数字字符串的长度。
第11题
下列关于函数的描述正确的是?
A:函数是可重复使用的,用来实现单一,或相关联功能的代码段
B:函数中必须return语句
C:函数好处是模块性,但不能提高代码的利用率
D:函数内容以冒号起始,可以不缩进
答案:A
函数是一段封装了特定功能的代码块,可以在程序中多次调用。函数的设计目的是为了实现特定的功能,并且具有模块化的特性,可以提高代码的可读性、可维护性和重用性。
第12题
调用以下函数时,语句“s=s+i”被执行的次数是?( )
def f():s=0i=1while i<10:if i%3==0 or s%2==1:s=s+ii=i+1print(s)
A:3
B:4
C:5
D:6
答案:C
在给定的代码中,s=s+i语句将在第3、4、5、6、9次循环迭代中执行。这是因为在这些迭代中,满足条件i%3==0 or s%2==1。
因此,s=s+i语句被执行的次数是5次。
第13题
已知有n本按照书名拼音排序好的图书,使用对分查找法搜索其中任何一本书,最多查找次数为6次,则n的值可能为?
A:20
B:50
C:80
D:110
答案:B
对规模为n的数据进行对分查找时,无论是否查找到,至多进行 |log2n|+1次(|log2n|表示小于等于log2n的最大整数),因此25≤n<26,即32≤n<64。
第14题
某程序代码设计如下,若输入整数5,则最终输出的结果为?( )
def fact(x):if x==1:s=1else:s=fact(x-1)*xreturn sn=int(input("请输入一个大于1的整数:"))print(fact(n)+fact(n-1))
A:120
B:24120
C:144
D:12024
答案:C
由于fact(5)=fact(4)*5, fact(4)=fact(3)*4, fact(3)=fact(2)*3, fact(2)=fact(1)*2, fact(1)=1,所以fact(5)+fact(4)=120+24=144。
第15题
用匿名函数方式求两个数中较大的数,下列定义语句格式正确的是?
A:result = lambda ‘x,y’: y if x> y else x
B:result= lambda x,y: y if x> y else x
C:result= lambda ‘x,y’: x if x> y else y
D:result= lambda x,y: x if x> y else y
答案:D
匿名函数的定义语法:lambda 参数:表达式语法。先写lambda关键字,然后依次写匿名函数的参数,多个参数中间用逗号连接,然后是一个冒号,冒号后面写返回的表达式。
第16题
下列程序段的正确运行结果是?( )
def fun(m,n):while m!=n:if m>n:m=m-nelse:n=n-mreturn mprint(fun(24,16))
A:4
B:8
C:-8
D:2
答案:B
自定义函数fun(m,n)的作用是求m,n两个整数的最大公约数。
第17题
运行下列程序,输出结果正确的是?( )
def fun(x,y=5):return x*ya=fun(10,10)print(a)
A:100
B:50
C:10
D:运行出错
答案:A
参数的默认值被替换。
第18题
如果需要在某函数内部调用上一层的局部变量,则可以使用( )关键字。
A:Local
B:nonlocal
C:global
D:nonglobal
答案:B
仅B可以调用上一层的局部变量
第19题
在Python程序中,设已定义函数op,它有一个整型传值参数,一个字符串型传值参数。设x,y为整型变量,z为字符串型变量,则下列能调用该函数的正确语句是?
A:op
B:op(x,y,z)
C:op x,y
D:op(x+y,z)
答案:D
在调用自定函数时需要用到“函数名<参数表>”的方法,且自定义函数op共有两个参数。
第20题
下列哪个语句段的时间复杂度最低?
A:
if n%2==0:x=x*2else:x=x+2
B:
n=1while n<=100:x=x+2
C:
for i in range(100):for j in range(10):x=x+2
D:
for i in range(100):for j in range(i):x=x+2
答案:A
时间复杂度按数量级递增顺序为:常数阶、对数阶、线性阶、线性对数阶、平方阶
第21题
下列哪个不是Python中的内建函数?
A:asc(x)
B:ord(x)
C:chr(x)
D:abs(x)
答案:A
Python中没有asc(x)这个内建函数,ord(x)函数的作用是返回x对应的ASCII值,chr(x)函数的作用是返回x对应的字符,abs(x)函数的作用是返回x的绝对值。
第22题
关于函数的定义语句,以下几项中正确的是?
A:def f(c=2,a,b):
B:def f(a,b=2,c):
C:def f(*c,**d,a,b):
D:def f(a,b,*c,**d):
答案:D
顺序实参必须要放在关键字实参之前,位置参数*args必须要在关键字参数**kwargs前,否则会程序报错。
第23题
下列关于递归的描述不正确的是?
A:递归函数一定包含条件控制语句
B:递归函数一定包含调用自身的语句
C:在调用自身函数时需要明确的边界终止条件
D:递归算法一般代码简洁,执行效率高,空间复杂度低
答案:D
递归算法并不一定代码简洁,执行效率高,或者空间复杂度低。实际上,在某些情况下,递归算法可能会导致代码冗长和执行效率低下,因为每次递归调用都涉及函数调用和堆栈操作。
第24题
下列哪个不是Python第三方库的pip安装方法?
A:使用pip命令
B:使用wheel命令
C:集成安装方法
D:文件安装方法
答案:B
第三方库安装
第25题
对于下列递归式子,当n=4时,F的值是?( )
F(n)=F(n-1)+3 F(1)=2
A:2
B:5
C:11
D:14
答案:C
用递归式子推导得出。
二、判断题(共10题,每题2分,共20分)
第26题
def add(a, b, c=0):return a+b+cprint(add(1, 2, 4))
这段程序的运行结果为3。
答案:错误
在调用函数时给函数提供了实参时,Python将使用指定的实参值
第27题
算法复杂度分析的目的是分析算法的效率,以求改进。
答案:正确
算法复杂度分析的目的是分析算法的效率,以便对算法进行改进。通过分析算法的复杂度,我们可以评估算法在输入规模增大时所需的时间和空间资源。这有助于我们比较不同算法的效率,并选择最优算法来解决问题。
因此,算法复杂度分析的目的是为了分析算法的效率,并找到改进的方法。
第28题
sum=0for i in range(5):sum=sum+iprint(sum)
运行以上程序,输出结果是15。
答案:错误
给定的代码计算了从0到4的累加和。然而,由于范围函数range(5)不包括上限值5,因此循环只会迭代0、1、2、3、4这五个数。
因此,输出结果将是10,而不是15。
第29题
已有函数def demo(*p):return sum§,表达式 demo(1, 2, 3, 4) 的值为10。
答案:正确
给定的函数demo(*p)使用了可变参数,可以接受任意数量的参数。在这个函数中,参数p被传递给sum()函数,用于计算所有参数的和。
因此,表达式demo(1, 2, 3, 4)将会将参数1、2、3、4传递给sum()函数,计算它们的和,结果是10。
第30题
使用python -m pip install --upgrade pip命令能够升级pip。
答案:正确
使用python -m pip install --upgrade pip命令可以升级pip。在命令行中执行此命令后,pip工具将会检查当前安装的pip版本,并尝试升级到最新版本。这是通过安装最新版本的pip包来实现的。
因此,给定的命令确实可以用于升级pip。
第31题
在python函数中,局部变量不能与全局变量重名。
答案:错误
当全局变量和局部变量同名时,首先会找程序内部有没有局部变量,如果有,则调用,如果没有,才会去调用全局变量。
第32题
下列程序段返回的值为“Hello!Python”。
lst="Hello!Python"def f():global lstlst="Hello!"return lstf()print(lst)
答案:错误
在函数f中,通过使用global关键字,我们将lst变量声明为全局变量。然后在函数内部,我们将其值修改为"Hello!"。最后,我们调用函数f()并打印全局变量lst的值。
因此,输出结果将是"Hello!“,而不是"Hello!Python”。函数内部的修改只会影响全局变量的值。
第33题
使用分治算法求解,子问题不能重复。
答案:正确
分治算法的子问题之间不可以包含公共的子问题。
第34题
设计一个程序来求xn(x的几次方)的值,算法思想是:把xn转换为xxn-1,而xn-1又可以转换为xxn-2,如此重复下去,直到x*x0,而x0=1,从而求出了xn的值。这个程序可以用递归来实现。
答案:正确
递归体现了“大事化小,小事化了”的思想,把大问题转换成小问题来解决,且有终止条件,即算法中的到x0=1为止。
第35题
下列程序段能正确打印1。
def f(a,b):a=a+bb=a-ba=a-breturn bprint(F(1,4))
答案:错误
Python中字母区分大小写,所以自定义函数创建和调用时,函数名要一致,否则调用不成功。
三、编程题(共3题,共30分)
第36题
利用分治思想,给定一个顺序表,编写一个求出其最大值的程序。
根据上述算法思想,补全下列代码。
输入输出示例:当顺序表是 [22,13,34,4,68,15,5,58,36],输出:68
def fun_max(num=list):return max(num)def fun(num):n = ① if n <= 2:return ② l_list, r_list = num[:n//2], num[n//2:]l_max, r_max = ③ return fun_max( ④ )if __name__ == "__main__":alist = [22,13,34,4,68,15,5,58,36]print(fun(alist))
答案:
def fun_max(num=list):return max(num)def fun(num):n = len(num)if n <= 2:return fun_max(num)l_list, r_list = num[:n//2], num[n//2:]l_max, r_max = fun(l_list), fun(r_list)return fun_max([l_max, r_max])if __name__ == "__main__":alist = [22,13,34,4,68,15,5,58,36]print(fun(alist))
评分标准:
① len(num) 或等效答案; (2分)
② fun_max(num) 或等效答案; (2分)
③ fun(l_list), fun(r_list) 或等效答案; (2分)
④ [l_max, r_max] 或等效答案;(2分)
第37题
现有n个人依次围成一圈玩游戏,从第1个人开始报数,数到第m个人出局,然后从出局的下一个人开始报数,数到第m个人又出局,…,如此反复到只剩下最后一个是胜利者。设n个人的编号分别为1,2,…,n,打印出局的顺序。
根据上述算法思想,补全下列代码。
输入输出示例:当n=10,m=4,输出如下:
出局的人是: 4
出局的人是: 8
出局的人是: 2
出局的人是: 7
出局的人是: 3
出局的人是: 10
出局的人是: 9
出局的人是: 1
出局的人是: 6
最后胜利者是: 5
def fun(n,k):L = list( ① )if n == 1:returnelse:x = 0for i in ② x = ③ - 1print('出局的人是:',L[x])del L[x]if x < 0:x = 0print('最后胜利者是:', ④ )fun(10,4)
答案:
def fun(n,k):L = list(range(1,n+1))if n == 1:returnelse:x = 0for i in range(n-1):x = (x + k) % len(L) - 1print('出局的人是:',L[x])del L[x]if x < 0:x = 0print('最后胜利者是:',L[0])fun(10,4)
评分标准:
① range(1,n+1) 或等效答案;(3分)
② range(n-1): 或等效答案;(3分)
③ (x + k) % len(L) 或等效答案;(3分)
④ L[0] 或等效答案;(3分)
第38题
设计一个算法,将一个正整数分解质因数。
程序分析:对n进行分解质因数,应先找到一个最小的质数k,然后按下述步骤完成:
(1)如果这个质数恰等于n,则说明分解质因数的过程已经结束,输出即可。
(2)如果n>k,但n能被k整除,则应打印出k的值,并用n除以k的商,作为新的正整数n,重复执行第一步。
(3)如果n不能被k整除,则用k+1作为k的值,重复执行第一步。
根据上述算法思想,补全下列代码。
输入输出示例:当n=105,输出:105= 357
当n=60,输出:60= 223*5
def fun(n):print('%d='%n,end=' ')for i in ① :while n!=i:if n>i and ② :print(i,end='*')③ else:breakelse:④ breakif __name__ == "__main__":while True:num=input("输入一个正整数:")if not num.isdigit():breakfun(int(num))
答案:
def fun(n):print('%d='%n,end=' ')for i in range(2,n+1):while n!=i:if n>i and n%i==0:print(i,end='*')n=n//ielse:breakelse:print(n)breakif __name__ == "__main__":while True:num=input("输入一个正整数:")if not num.isdigit():breakfun(int(num))
评分标准:
① range(2,n+1) 或等效答案;(3分)
② n%i==0 或等效答案;(3分)
③ n=n//i 或等效答案;(2分)
④ print(n) 或等效答案;(2分)
相关文章:

2021年03月 Python(四级)真题解析#中国电子学会#全国青少年软件编程等级考试
Python等级考试(1~6级)全部真题・点这里 一、单选题(共25题,每题2分,共50分) 第1题 不超过100个元素的有序数列,使用二分查找能找到指定的元素,可能的查找次数不包括? …...

2023.10.18 信息学日志
1. CF1689D Lena and Matrix 题目描述 n ⋅ m n \cdot m n⋅m 的矩阵,求矩阵上任意一点坐标使得到矩阵上的关键点曼哈顿距离最大值最小。数据范围: ∑ n ⋅ m ≤ 1 0 6 \sum n \cdot m \leq 10^6 ∑n⋅m≤106 题目概况 来源:Codeforces …...
)
Modbus封装库(Com,tcp,udp一应俱全)
自行封装在用的Modbus通迅库,集成了com,tcp,udp, 做个笔记吧, 以下头文件, #pragma once #include <functional> #include <vector> #include <string> #include <memory> #ifdef LIBMODBUS_EXPORTS #define LIBMODBUS_EXPORT_…...

专访HuggingFace CTO:开源崛起、创业故事和AI民主化丨智源独家
导读 HuggingFace CTO Julien Chaumond认为,在大模型时代,AI民主化至关重要。随着大语言模型和复杂人工智能系统的崛起,持续提升AI技术的可及性有助于确保这些技术的获取和控制不集中在少数强大实体手中。技术民主化促进了机会均等࿰…...
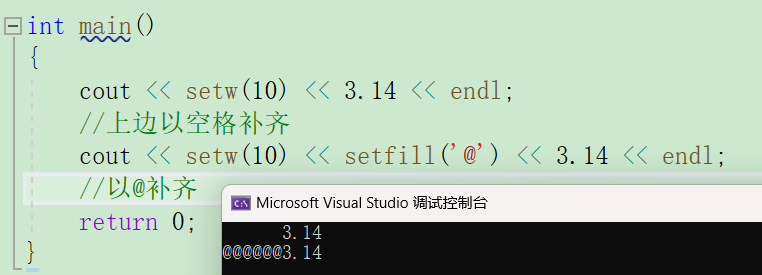
C++常用格式化输出转换
在C语言中可以用printf以一定的格式打印字符,C当然也可以。 输入输出及命名空间还不太了解的小伙伴可以看一看C入门讲解第一篇。 在C中,可以用流操作符(stream manipulators)控制数据的输出格式,这些流操作符定义在2…...

如何使用 Loadgen 来简化 HTTP API 请求的集成测试
引言 在编写 HTTP 服务的过程中,集成测试 1 是保证程序正确性的重要一环,如下图所示,其基本的流程就是不断向服务发起请求然后校验响应的状态和数据等: 为大量的 API 和用例编写测试是一件繁琐的工作,而 Loadgen 2 正…...

软件测试面试大家是不是一问到项目就不会了?
软件测试面试中,介绍做过的项目,可以说是必不可少的一道面试题了,对于面试的同学来说,该自己发挥呢? 把项目的所有功能噼里啪啦说一遍就完事了?当然不是,我们要搞清楚,面试官问这个…...

伐木猪小游戏
欢迎来到程序小院 伐木猪 玩法:控制小猪点击屏幕左右砍树,不能碰到树枝,考验手速与眼力,记录分数,快去挑战伐木吧^^。开始游戏https://www.ormcc.com/play/gameStart/199 html <script type"text/javascript…...
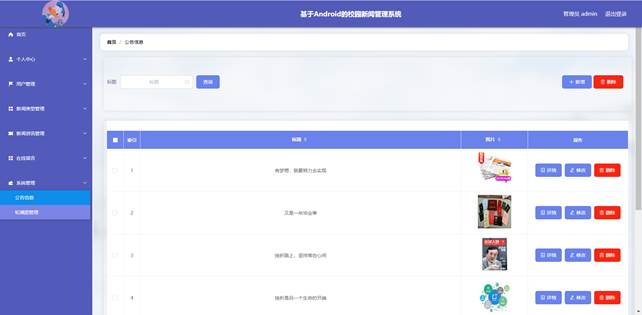
0007Java安卓程序设计-ssm基于Android的校园新闻管理系统
文章目录 **摘** **要**目 录开发环境 编程技术交流、源码分享、模板分享、网课教程 🐧裙:776871563 摘 要 网络的广泛应用给生活带来了十分的便利。所以把校园新闻管理与现在网络相结合,利用java技术建设校园新闻管理系统app,实…...
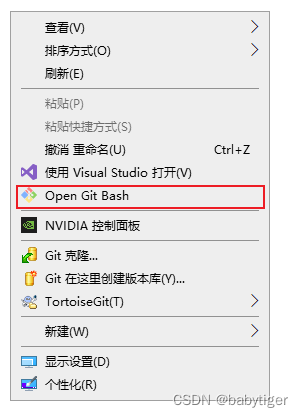
git增加右键菜单
有次不小心清理系统垃圾,把git右击菜单搞没了,下面是恢复方法 将下面代码存为.reg文件,双击后导出生效,注意,你安装的git必须是默认C盘的,如果换了地方要改下面注册表文件中相关的位置 Windows Registry …...

openGauss学习笔记-117 openGauss 数据库管理-设置数据库审计-查看审计结果
文章目录 openGauss学习笔记-117 openGauss 数据库管理-设置数据库审计-查看审计结果117.1 前提条件117.2 背景信息117.3 操作步骤 openGauss学习笔记-117 openGauss 数据库管理-设置数据库审计-查看审计结果 117.1 前提条件 审计功能总开关已开启。需要审计的审计项开关已开…...

学习代码20231106
解释代码:os.environ[“OMP_NUM_THREADS“] “1“ 这行代码涉及到 Python 的 os 模块和环境变量。它的作用是设置名为 “OMPNUMTHREADS” 的环境变量的值为 “1”。让我解释一下各部分的含义: 1.os.environ: 这是 Python 中的一个字典,包含…...

turtle绘制分形树-第10届蓝桥杯省赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第5讲。 turtle绘制分形树&…...

【大厂招聘试题】__硬件工程师_2021年“美团”校招
目录 匹配职位:硬件工程师 1.(多选题)单处理系统中,进程P1,P2,P3处于就绪队列,进程P4,P6处于等待队列,P5正占用处理器运行,以下对接下来的运行合理的分析是( ÿ…...

算法通关村第七关|黄金挑战|迭代实现二叉树的前、中、后序遍历
1.迭代实现前序遍历 public List<Integer> preOrderTraversal(TreeNode root) {List<Integer> res new ArrayList<Integer>();if (root null) {return res;}Deque<TreeNode> stack new LinkedList<TreeNode>();TreeNode node root;while (!…...

了解高防服务器的工作原理
在当今互联网时代,网络安全问题日益突出,各种网络攻击层出不穷。为了保护企业的网络安全,高防服务器应运而生。那么,你是否了解高防服务器的工作原理呢?下面就让我们一起来探索一下。 高防服务器是一种能够有效抵御各种网络攻击的…...

AVL树性质和实现
AVL树 AVL是两名俄罗斯数学家的名字,以此纪念 与二叉搜索树的区别 AVL树在二叉搜索树的基础上增加了新的限制:需要时刻保证每个树中每个结点的左右子树高度之差的绝对值不超过1 因此,当向树中插入新结点后,即可降低树的高度&…...

出口贸易媒体发稿推广6个技巧提升品牌知名度-华媒舍
1. 出口贸易媒体介绍 出口贸易媒体是指专注于报道国际贸易、跨境业务和进出口市场的媒体平台。这些媒体对于企业发展来说至关重要,可以帮助品牌扩大影响力、提升知名度,促进商业合作。下面介绍6个出口贸易媒体发稿推广技巧,帮助企业更好地利…...
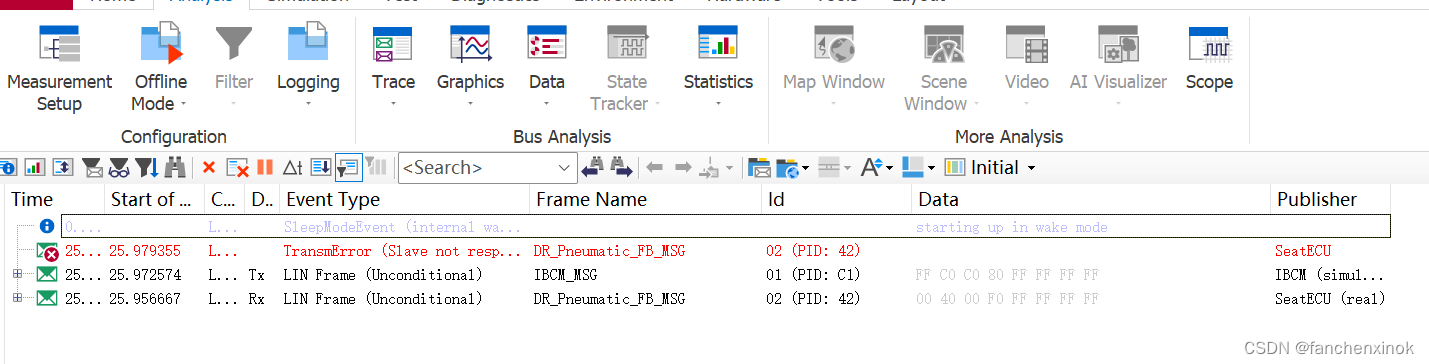
学习笔记:CANOE模拟LIN主节点和实际从节点进行通信测试
先写点感想,在LIN开发阶段,我一般用图莫斯USB工具来进行模拟主机节点发送数据。后来公司买了CANOE工具就边学习边搭建了LIN的测试工程,网上的资料真的很少,主要是靠自己一点点摸索前进,总算入门。几个月后的今天&#…...
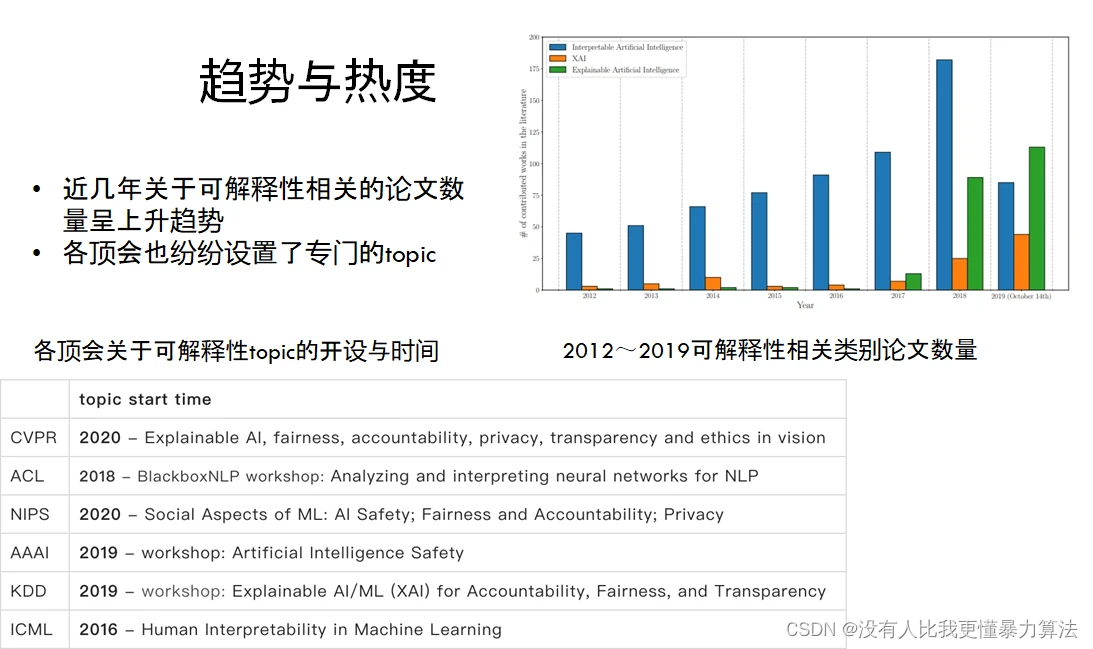
模型可解释性
模型可解释性 前言导读Background1、为什么需要可解释性?2、诞生背景3、研究现状4、常见的模型可解释性方法4.1 基于模型自身的可解释性1)Explanation Generation2)Prototype Network 4.2 基于结果的可解释性 5、应用前景6、面临挑战 前言导读…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
