图论——并查集
参考内容:
图论——并查集(详细版)
并查集(Disjoint-set)是一种精巧的树形数据结构,它主要用于处理一些不相交集合的合并及查询问题。一些常见用途,比如求联通子图、求最小生成树的 Kruskal 算法和求最近公共祖先(LCA)等。
并查集的理念是只关注个体属于哪个阵营,并不关心这个阵营中个体内部的关系,比如我们常说的张三是李家沟的,王二是王家坝的。同时并查集借助个体代表集体的思想,用一个元素代表整个群体,就像我们开学都会有学生代表、教师代表讲话一样,在台上讲话的那一个学生就代表了学校所有的学生。
并查集基本操作
并查集的基本操作主要有初始化 init、查询 find和合并 union操作。
初始化
在使用并查集的时候,常常使用一个数组fa来存储每个元素的父节点,在一开始的时候所有元素与其它元素都没有任何关系,即大家相互之间还不认识,所以我们把每个元素的父节点设为自己。
#define ARR_LEN 6000int fa[ARR_LEN];void init(int n)
{for(int i = 1; i <= n; i++)fa[i] = i;
}
查询
查询即找到指定元素的祖先。需要注意的是,这里我们需要找到指定元素的根祖先,不能找到爸爸或者爷爷就停止了,而是要找到查找不下去了为止,所以要不断的去递归下去,直到找到父亲为自己的结点才结束。
int find(int i)
{if(i == fa[i]) // 递归出口return i;elsereturn find(fa[i]); // 不断向上查找祖先
}
考虑下面的场景,假如第一次我们需要查询元素5的祖先,第二次需要查询元素4的祖先,会发现第一次查询包含了第二次查询的计算过程,但我们的程序却傻傻的计算了两次,有没有办法去来优化查询过程,让每一次查询都能利用到此前查询计算的便利?

考虑到并查集并不关心某个元素的爸爸、爷爷是谁,只关心最终的祖先是谁,所以我们可以在查询的过程中顺便做一些修改,比如在查询5的过程中,顺便就把4和2的父亲给修改为1,即我们在查找过程中进行路经压缩
int find(int i)
{if(i == fa[i]){return i;} else {fa[i] = find(fa[i]); // 进行路径压缩return fa[i];}
}
合并
合并操作即介绍两个人相互认识,将他们纳入同一个帮派,只需要将俩元素的父亲修改为同一个即可。
void union(int i, int j)
{int fa_i = find(i);int fa_j = find(j);fa[fa_i] = fa_j;
}
相关练习题目
洛谷 P1551 亲戚
题目连接:https://www.luogu.com.cn/problem/P1551
题目描述
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
规定: x x x 和 y y y 是亲戚, y y y 和 z z z 是亲戚,那么 x x x 和 z z z 也是亲戚。如果 x , y x,y x,y 是亲戚,那么 x x x 的亲戚都是 y y y 的亲戚, y y y 的亲戚也都是 x x x 的亲戚。
输入格式
第一行:三个整数 n , m , p , ( n , m , p ≤ 5000 ) n,m,p,(n,m,p≤5000) n,m,p,(n,m,p≤5000) 分别表示有 n n n 个人, m m m 个亲戚关系,询问 p p p 对亲戚关系。
以下 m m m 行:每行两个数 M i , M j , 1 ≤ M i , M j ≤ n M_i,M_j,1≤M_i,M_j≤n Mi,Mj,1≤Mi,Mj≤n,表示 M i M_i Mi 和 M j M_j Mj 具有亲戚关系。
接下来 p p p 行:每行两个数 P i , P j P_i,P_j Pi,Pj,询问 P i P_i Pi 和 P j P_j Pj 是否具有亲戚关系。
输出格式
p p p 行,每行一个Yes或No。表示第 i i i 个询问的答案为“具有”或“不具有”亲戚关系。
输入输出样例
# 输入
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6# 输出
Yes
Yes
No
题目解析
可以发现这是一个非常标准的并查集问题,简直和并查集模版如出一辙,因此直接将所有关系读取后进行合并,然后直接查询父亲是否为同一个即可。
#include<bits/stdc++.h>
using namespace std;#define ARR_LEN 6000int fa[ARR_LEN];void init(int n)
{for(int i = 1; i <= n; i++)fa[i] = i;
}int find(int i)
{if(i == fa[i]){return i;} else {fa[i] = find(fa[i]);return fa[i];}
}void union(int i, int j)
{int fa_i = find(i);int fa_j = find(j);fa[fa_i] = fa_j;
}int main()
{int n, m, p;int a, b;cin>> n >> m >> p;init(n);for(int i = 0; i < m; i++){cin >> a >> b;union(a, b);}for(int i = 0; i < p; i++){cin >> a >> b;int fa_a = find(a);int fa_b = find(b);if(fa_a == fa_b)cout<<"Yes"<<endl;elsecout<<"No"<<endl;}
}
杭电 OJ1213 How Many Tables
题目连接:https://acm.hdu.edu.cn/showproblem.php?pid=1213
题目描述
Today is Ignatius’ birthday. He invites a lot of friends. Now it’s dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.
One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.
For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.
输入格式
The input starts with an integer T ( 1 < = T < = 25 ) T(1<=T<=25) T(1<=T<=25) which indicate the number of test cases. Then T T T test cases follow. Each test case starts with two integers N N N and M ( 1 < = N , M < = 1000 ) M(1<=N,M<=1000) M(1<=N,M<=1000). N N N indicates the number of friends, the friends are marked from 1 1 1 to N N N. Then M M M lines follow. Each line consists of two integers A A A and B ( A ! = B ) B(A!=B) B(A!=B), that means friend A A A and friend B B B know each other. There will be a blank line between two cases.
输出格式
For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.
输入输出样例
# 输入
2
5 3
1 2
2 3
4 55 1
2 5# 输出
2
4
题目解析
分析可以发现,这个问题要我们做的是统计在所有元素合并之后,统计总共有多个和集合。很轻松就能写出下面的 AC 代码。类似的问题还有杭电 OJ1232 畅通工程。
读者大人可以在此基础上继续进行延伸,我们实际生活中每个桌子只能坐 8 个人,假设还需要考虑每桌人数的容量,又如何进行改进呢?
#include<bits/stdc++.h>
using namespace std;#define ARR_LEN 6000int fa[ARR_LEN];void init(int n)
{for(int i = 1; i <= n; i++)fa[i] = i;
}int find(int i)
{if(i == fa[i]){return i;} else {fa[i] = find(fa[i]);return fa[i];}
}void union(int i, int j)
{int fa_i = find(i);int fa_j = find(j);fa[fa_i] = fa_j;
}int main()
{int n, m, a, b, t;cin>>t;for(int i = 0; i < t; i++){cin>>n>>m;int ans = 0;init(n);for(int i = 0; i < m; i++) {cin>>a>>b;union(a, b);}for(int i = 1; i <= n; i++) {// 如果父亲是自己,那么就表示一个独立的集合if(find(i) == i)ans++;}cout<<ans<<endl;}}
杭电 OJ1272 小希的迷宫
题目连接:https://acm.hdu.edu.cn/showproblem.php?pid=1272
题目描述
小希设计了一个迷宫让 Gardon 玩,首先她认为所有的通道都应该是双向连通的,就是说如果有一个通道连通了房间 A 和 B,那么既可以通过它从房间 A 走到房间 B,也可以通过它从房间 B 走到房间 A,为了提高难度,小希希望任意两个房间有且仅有一条路径可以相通(除非走了回头路)。小希现在把她的设计图给你,让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子,前两个是符合条件的,但是最后一个却有两种方法从 5 到达 8。
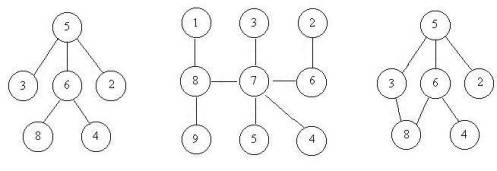
输入格式
输入包含多组数据,每组数据是一个以 0 0 结尾的整数对列表,表示了一条通道连接的两个房间的编号。房间的编号至少为 1,且不超过 100000。每两组数据之间有一个空行。整个文件以两个 -1 结尾。
输出格式
对于输入的每一组数据,输出仅包括一行。如果该迷宫符合小希的思路,那么输出Yes,否则输出No。
输入输出样例
# 输入
6 8 5 3 5 2 6 4
5 6 0 08 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 03 8 6 8 6 4
5 3 5 6 5 2 0 0-1 -1# 输出
Yes
Yes
No
题目解析
其实这个问题就是让我们判断一个连通图中是否存在环,那么问题就转换为寻找出现环的条件。其实不难发现出现下面两种情况时,连通图即存在环。
- 在查找过程中,发现两个不同元素的父亲是相同的;
- 若不存在环,则边的数量一定比顶点数量少 1。
#include<bits/stdc++.h>
using namespace std;#define ARR_LEN 100010int fa[ARR_LEN];
bool visited[ARR_LEN]; // 用于辅助记录顶点的数量
int edges, points; // 记录顶点和边的数量
bool hascycle; // 是否存在环void init()
{hascycle = false;edges = 0;points = 0;for(int i = 1; i < ARR_LEN; i++)fa[i] = i, visited[i] = false;
}int find(int i)
{if(i == fa[i]){return i;} else {fa[i] = find(fa[i]);return fa[i];}
}void union(int i, int j)
{int fa_i = find(i);int fa_j = find(j);// 两个元素祖先相同,存在环if(fa_i == fa_j) {hascycle = true;} else {visited[i] = true;visited[j] = true;edges++;fa[fa_i] = fa_j;}
}int main()
{int a, b;init();while(cin>>a>>b) {if(a == 0 && b == 0) {cout<<"Yes"<<endl;continue;}if(a == -1 && b == -1) {return 0;}union(a, b);while(cin>>a>>b){if(a == 0 && b == 0) {break;}union(a, b);}if(hascycle) {cout<<"No"<<endl;continue;}for(int i = 1; i < ARR_LEN; i++){if(visited[i]) {points++;}}if(points == edges + 1) {cout<<"Yes"<<endl;} else {cout<<"No"<<endl;}init();}
}
相关文章:

图论——并查集
参考内容: 图论——并查集(详细版) 并查集(Disjoint-set)是一种精巧的树形数据结构,它主要用于处理一些不相交集合的合并及查询问题。一些常见用途,比如求联通子图、求最小生成树的 Kruskal 算法和求最近公共祖先&…...

计算机毕业设计java+vue+springboot的论坛信息网站
项目介绍 本论文系统地描绘了整个网上论坛管理系统的设计与实现,主要实现的功能有以下几点:管理员;首页、个人中心、用户管理、公告管理、公告类型管理、热门帖子管理、帖子分类管理、留言板管理、论坛新天地、我的收藏管理、系统管理&#…...

.net core添加SQL日志输出
GreDbContext : Microsoft.EntityFrameworkCore.DbContext 下添加 public static readonly ILoggerFactory MyLoggerFactory LoggerFactory.Create(builder > { builder.AddConsole(); }); protected override void OnConfiguring(DbContextOptionsBuilder optionsBuilder…...
虚幻5.1 常见的效果关闭方式
常见的虚幻效果关闭方式 1.Bloom ProjectSettings->Rendering->Default Settings->Bloom PostProcessVolume->Lens->Bloom 2.Ambient Occlusion/Screen Space Ambient Occlusion(SSAO) ProjectSettings->Rendering->Default Settings->Ambient Occl…...

每日一题 --- 力扣318----最大单词长度乘积
这道题时间复杂度我感觉设置的不是很好,应该最好是有一个1000变成10000就行。 因为我在做这道题的时候被误导了,以为双重循环暴力判断一下也能过,因为1000*1000 *26的时间复杂度没有到1亿,那么我刚开始认为是能过的,结…...

掌动智能性能压力测试优势有哪些
企业通过自动化的测试工具模拟多种正常、峰值以及异常负载条件来对系统的各项性能指标进行测试。本文将介绍性能压力测试的价值及主要优势! 一、性能压力测试的价值 1、评估系统能力:有助于参数的基准测试,可以度量系统的响应时间;还有助于检查系统是否可…...
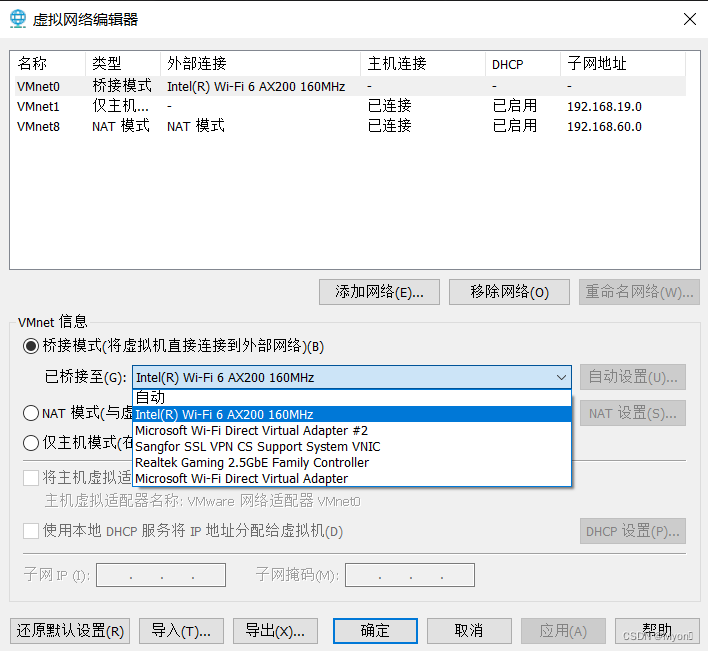
虚拟机没有桥接模式--物理机WiFi不见了--注册表修复
我们知道虚拟机有三种模式: vmnet0 桥接模式;vmnet1 仅主机模式;vmnet8 NAT模式 我自己以前一直用的NAT模式,今天突然要用到桥接模式,发现无法切换... 我下面这个是后面弄好了的,最开始是没有显示桥接模式…...
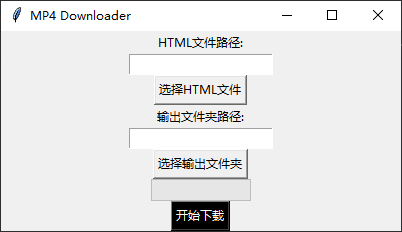
【Python】批量下载素材酷视频资源
【需求】 做视频精彩需要用到梗图视频等,但是素材酷上面的视频没有搜索功能,每次用起来还要去下载也很麻烦,下载只能一个一个下载也很麻烦,下要搞一个能够批量下载的功能,然后把下载的资源全部放进万兴喵影编辑器的云空间,这样就可以做到随做随查随用了。 【效果】 目…...

QuantLib学习笔记——一个简单的价值估算案例
⭐️ 前言 QuantLib很强大,它实现了很多金融工具及其价值估算方法,从最简单的折现模型,到利用BSM模型对期权进行定价,覆盖面相当齐全。本文以一个简单的净现值估算案例,开启笔者金融工具估值的旅程。 开上豪车&#…...

智能语音和自然语言处理技术
一、定义 智能语音和自然语言处理技术是指通过计算机技术实现人机交互的一种技术。它可以让计算机和人类之间进行自然而流畅的交流,从而实现更高效、更便捷、更智能的信息交流和处理。 智能语音和自然语言处理技术主要包括语音识别、语音合成、自然语言理解、自然…...
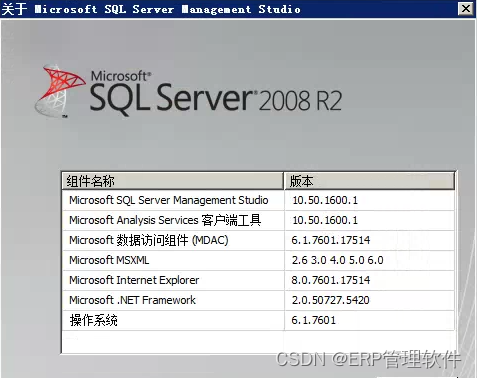
【Sql】sql server数据库提示:执行Transact-SQL语句或批处理时发生了异常。 无法打开数据库msdb,错误:926。
【问题描述】 打开sql server2008r2数据库的时候, 系统提示执行Transact-SQL语句或批处理时发生了异常。 无法打开数据库msdb,错误:926。 【概念理解】 首先MSDB数据库是的作用: 用于给SQL Server代理提供必要的信息来运行调度警…...
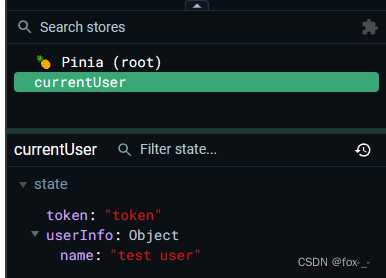
Day 5 登录页及路由 (三) 基于axios的API调用
系列文章目录 本系列记录一下通过Abp搭建后端,VueElement UI Plus搭建前端,实现一个小型项目的过程。 Day 1 Vue 页面框架Day 2 Abp框架下,MySQL数据迁移时,添加表和字段注释Day 3 登录页以及路由 (一)Day 4 登录页以…...
雷神学习---视音频数据处理入门:RGB、YUV像素数据处理
原文地址:https://blog.csdn.net/leixiaohua1020/article/details/50534150 从代码可以看出,如果想把YUV格式像素数据变成灰度图像,只需要将U、V分量设置成128即可。 这是因为U、V是图像中的经过偏置处理的色度分量。色度分…...

Asp.Net Core服务端处理请求过来的压缩格式
之前是直接传没有经过压缩的文件字节,有时文件过大的话,可能占宽带就多,宽带流量都是钱。后来有个想法,在客户端把文件进行压缩,把压缩的文件流发给服务端进行解压。 1,先修改项目中Startup.cs文件中Confi…...

自定义指令
二、自定义指令 1.指令介绍 内置指令:v-html、v-if、v-bind、v-on… 这都是Vue给咱们内置的一些指令,可以直接使用 自定义指令:同时Vue也支持让开发者,自己注册一些指令。这些指令被称为自定义指令 每个指令都有自己各自独立的功…...

仿真实现lio_sam建图和ndt_matching定位
文章目录 一、仿真环境二、lio_sam建图1.修改配置文件2.开始建图 三、ndt_matching定位1.新建启动文件2.启动 总结 一、仿真环境 使用现有开源的仿真环境—从零开始搭建一台ROS开源迷你无人车,作者已经配置好小车模型以及gazebo环境,imu频率已改为200HZ…...
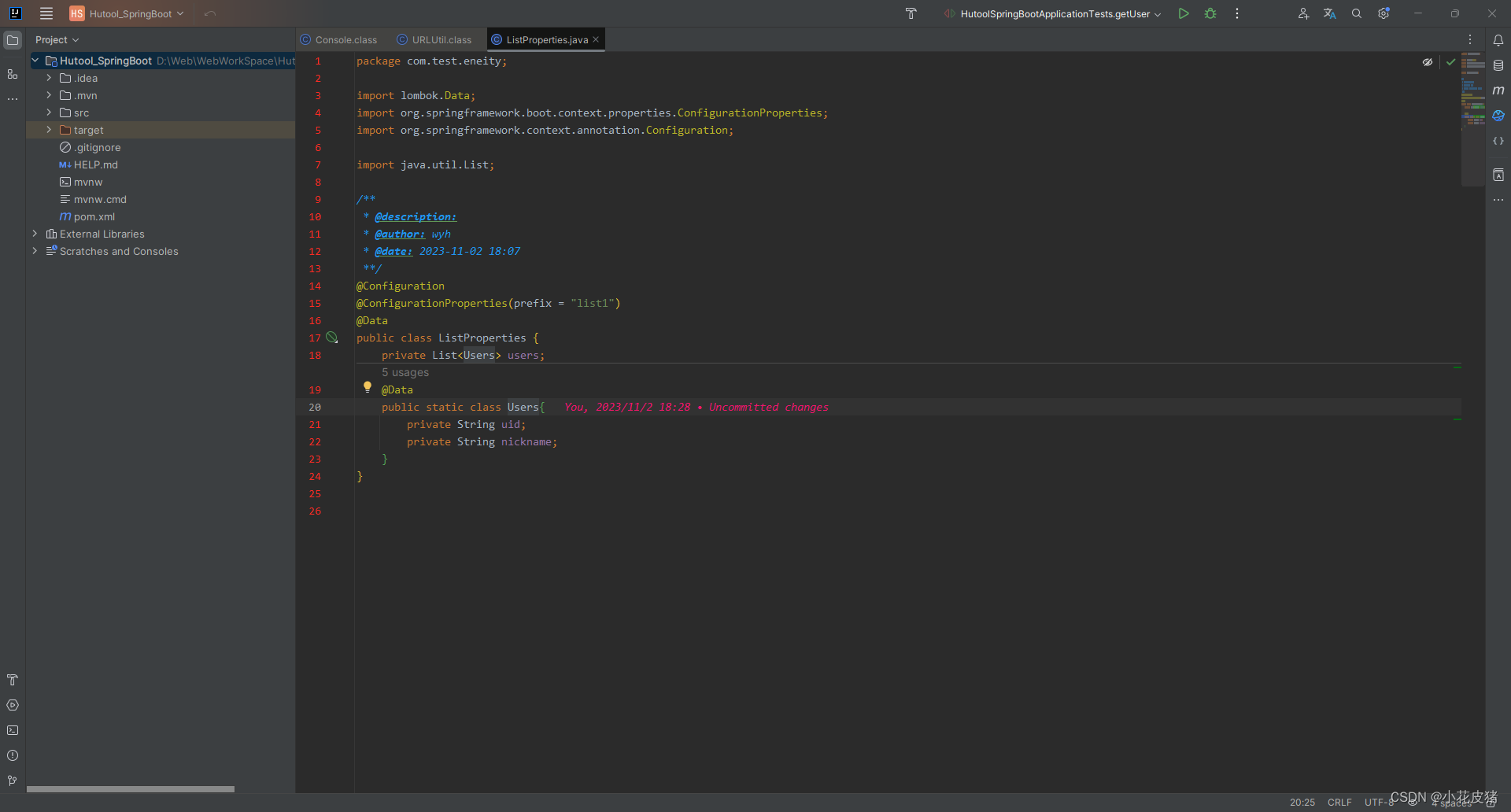
IDEA取消git对项目的版本控制
前言 前几天新建项目的时候不小心选了个git仓库,导致这个测试项目一直被git管理着。 解决办法 1 右键项目 选择打开资源目录 2 删除.git文件 把目录下的.git文件删掉 3 删除idea中的git管理 删除完.git文件后,进入idea,右下角会有这样的提…...

如何聪明地编写测试
作者|Maxim Schepelin Booking公司软件开发工程师 编译整理|TesterHome 以下为作者观点: 在我(作者)的职业生涯中,我多次看到团队如何开始自动化测试,当然并非所有尝试都成功。在这篇文章中…...

CF1866M Mighty Rock Tower
CF题面 luogu题面 期望题。 题目大意:一个人在搭积木,每次堆叠可能成功或失败,失败可能导致其下面连续的若干块掉落。给定搭每一块时失败的概率,求堆叠完成的期望次数。 具体的,假设当前正在堆叠第 i 块,…...
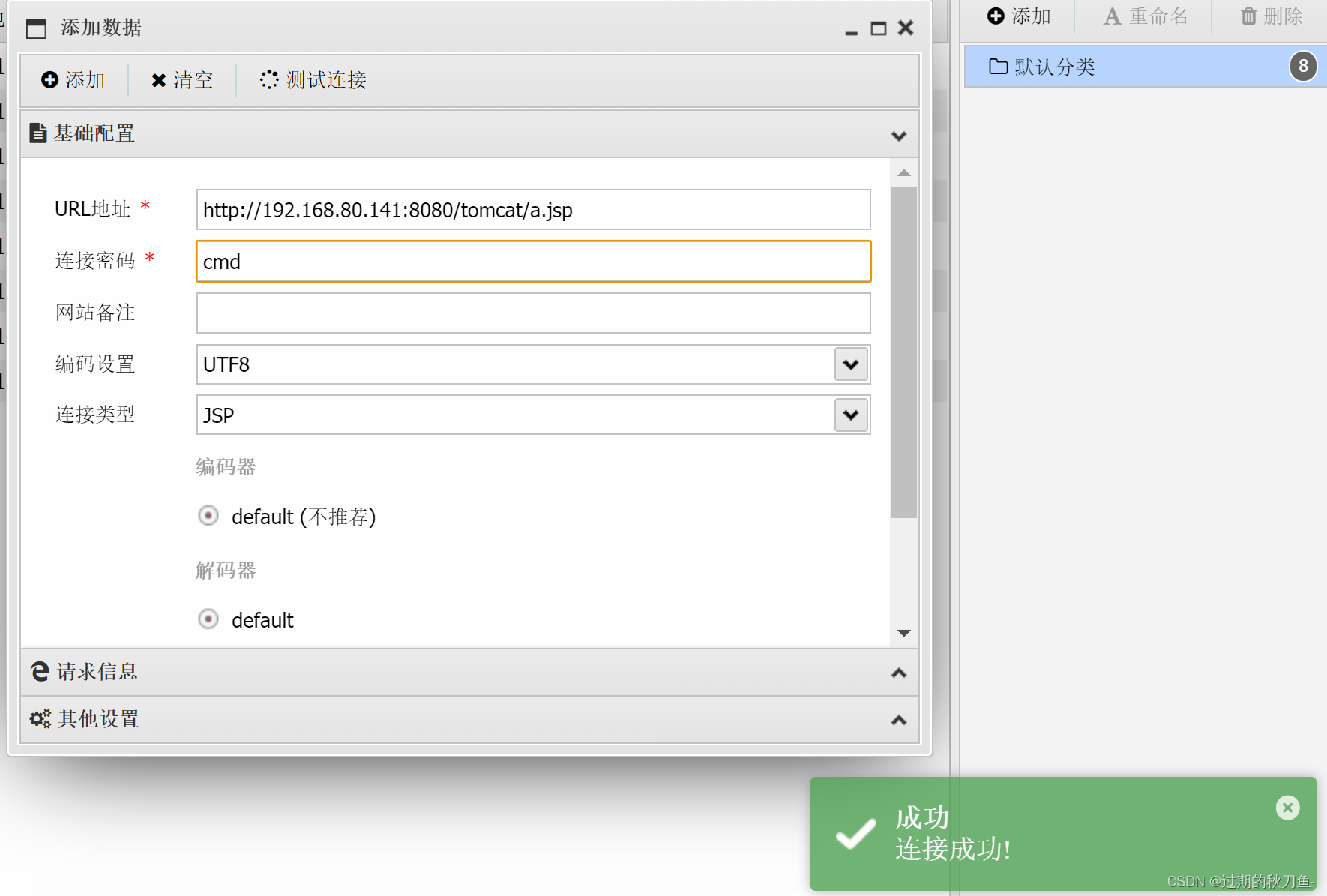
【漏洞复现】Apache_Tomcat7+ 弱口令 后台getshell漏洞
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现1、基础环境2、漏洞扫描3、漏洞验证 说明内容漏洞编号漏洞名称Tomcat7 弱口令 && 后台getshell漏洞漏洞评级高…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
