基于卷积优化算法的无人机航迹规划-附代码
基于卷积优化算法的无人机航迹规划
文章目录
- 基于卷积优化算法的无人机航迹规划
- 1.卷积优化搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用卷积优化算法来优化无人机航迹规划。
1.卷积优化搜索算法
卷积优化算法原理请参考:https://blog.csdn.net/u011835903/article/details/130000907
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得卷积优化搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用卷积优化算法对航迹评价函数式(7)进行优化。优化结果如下:


从结果来看,卷积优化算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于卷积优化算法的无人机航迹规划-附代码
基于卷积优化算法的无人机航迹规划 文章目录 基于卷积优化算法的无人机航迹规划1.卷积优化搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用卷积优化算法来优化无人机航迹规划。 …...

科技云报道:不卷自研大模型,金山办公如何创新生成式AI?
科技云报道原创。 过去大半年里,很多人对大模型的前景寄予厚望。主流观点认为,每个行业、每款产品都可以通过大模型“重做一遍”。 “重做一遍”听起来想象空间很大,但实际上多数大模型产品需要漫长的训练周期和海量资源投入,落…...

3BHE022291R0101 PCD230A 专注于制造卓越人工智能
3BHE022291R0101 PCD230A 专注于制造卓越人工智能 BISTelligence是BISTel的一个分支,BISTel是为全球半导体和FPD制造商提供工程和软件自动化产品的领先供应商。半导体产品集团上个月被卖给了新思科技。在出售给Synopsys之后,Bisetlliegnce成立了两个部门…...

小程序 scroll-view 性能问题
先说使用场景,一次加载很多数据造成小程序卡顿的问题 ,找了好多都没有好的解决办法,要么太过复杂,然后研究了两天通过简单的办法实现,先根据数量把高度撑开,然后根据滚动位置渲染指定的数据就可以了&#x…...
【移远QuecPython】EC800M物联网开发板的硬件PWM和PWM输出BUG
【移远QuecPython】EC800M物联网开发板的硬件PWM和PWM输出BUG 文章目录 导入库初始化PWM开启PWMPWM硬件BUG硬件BUG复现原因附录:列表的赋值类型和py打包列表赋值BUG复现代码改进优化总结 py打包 导入库 from misc import PWM_V2或者 from misc import PWM但我觉得…...

OverDraw的优化
在uwa搜寻到的一些overDraw优化方法 透明图片避免绘制来减少overDraw 像一些alpha0的图片,根本没有必要参与绘制。所以留一些可以参与Raycast,但是不绘制 using UnityEngine; using System.Collections;namespace UnityEngine.UI {public class Empty…...

数据结构—字符串
文章目录 7.字符串(1).字符串及其ADT#1.基本概念#2.ADT (2).字符串的基本操作#1.求子串substr#2.插入字符串insert#3.其他操作 (3).字符串的模式匹配#1.简单匹配(Brute-Force方法)#2.KMP算法I.kmp_match()II.getNext() #3.还有更多 小结附录:我自己写的string 7.字符…...

inne所属公司抢注“童年时光”商标仍被冻结
根据中国商标网查询,国家知识产权局已于2023年3月10日裁定,被告inne所属的南京童年时光生物技术有限公司注册的“童年时光”商标无效。随着这起保健品行业品牌资产争夺事件的发酵,更多的细节得到披露,至此,一个从“代理…...

20231106-前端学习加载和视频球特效
加载效果 代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>加载效果</title><!-- 最新…...

Arrays.asList() 和 List.of() 的列表之争
1. 概述 有时在Java中,为了方便,我们需要创建一个小列表或将数组转换为列表。Java 为此提供了一些辅助方法。 在本文中,我们将比较初始化小型临时数组的两种主要方法:List.of()和 Array.asList()。 2. Arrays.asList() Java 自…...
基于51单片机的停车场管理系统仿真电路设计
**单片机设计介绍,基于51单片机的停车场管理系统仿真电路设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 停车场管理系统仿真电路设计介绍 停车场管理系统主要用于自动化管理和控制停车场,以提高停车…...

APIView单一资源的查看更新删除
APIView单一资源的查看更新删除 一、构建路由 re_path("author/(/d)",AuthorDetailView.as_view)), 二、视图类 在views.py中添加AuthorDetailView类 class AuthorDetailView(APIView):def get(self, request, pk):author Author.objects.get(pkpk)serializer A…...

UML--类图的表示
1. 类的表示 1.1 访问属性 : public -: private #: protected 1.2 接口与抽象类 斜体 表示抽象类和抽象方法 <<Interface>> 类表示接口 1.3 类图示意 Mclass- val: int getVal(): int 2. 类关系 2.1 实现关系 空心三角形和虚线组成 B实现A,则三角形尖尖朝…...
JVM字节码文件浅谈
文章目录 版权声明java虚拟机的组成字节码文件打开字节码文件的姿势字节码文件的组成魔数(基本信息)主副版本号(基本信息)主版本号不兼容的错误解决方法基本信息常量池方法 字节码文件的常用工具javap -v命令jclasslib插件阿里art…...
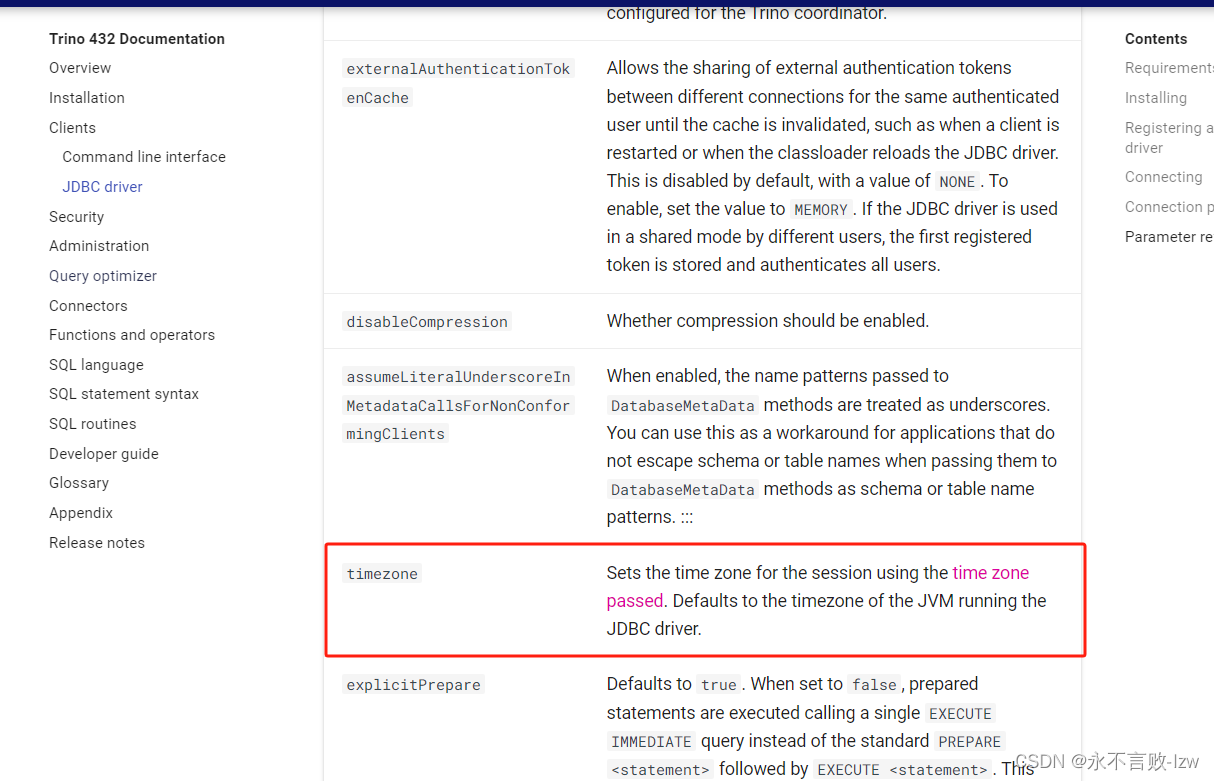
DBever 连接trino时区问题 The datetime zone id ‘GMT+08:00‘ is not recognised
DBever连接trino 测试连接成功,但是执行sql报时区不对、如果你默认使用的是大于jdk8的版本 会存在这个问题,因为jdk版本 jdk8 和jdk17 版本默认时区是不同的 trino官网明确说明了时区默认跟jdk走 解决方案 可以先行查看JDK本地时区库版本,执…...

xlua源码分析(二)lua Call C#的无wrap实现
xlua源码分析(二)lua Call C#的无wrap实现 上一节我们主要分析了xlua中C# Call lua的实现思路,本节我们将根据Examples 03_UIEvent,分析lua Call C#的底层实现。例子场景里有一个简单的UI面板,面板中包含一个input fie…...

MySql优化经验分享
一条sql的具体执行过程 连接 我们怎么查看MySQL当前有多少个连接? 可以用show status命令,模糊匹配Thread, Show global status like "Thread%" show global variables like wait timeout;—非交互式超时时间,如JDBC…...
【Linux】:使用git命令行 || 在github创建项目 || Linux第一个小程序——进度条(进阶版本)
在本章开始之前还是先给大家分享一张图片 这是C的笔试题 感兴趣的同学可以去试一试 有难度的哟 也可以直接在牛客网直接搜索这几道题目哈 好了今天我们正式进入我们的正题部分 🕖1.使用git命令行 安装git yum install git🕠2.在github创建项目 使用…...

Kotlin apply 交换两个数
代码: fun main() {var a 1var b 2a b.apply {b aprintln("$b")println("$this")}println("$a $b") }打印结果: 1 2 2 1原理分析: /*** Calls the specified function [block] with this value as its r…...

Android jetpack : Navigation 导航 路由 、 单个Activity嵌套多个Fragment的UI架构方式
Android Navigation 如何动态的更换StartDestination &&保存Fragment状态 Navigation(一)基础入门 google 官网 : Navigation 导航 路由 讨论了两年的 Navigation 保存 Fragment 状态问题居然被关闭了 Navigation是一种导航的概念,即把Activ…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
