SLAM中求导相关的公式总结
李代数与李群的关系
R ˙ R T \dot{R}R^{T} R˙RT 是一个反对称矩阵,所以这个矩阵可以用一个1×3向量进行反对称来表示
R ˙ R T = Φ ^ \dot{R}R^{T}=Φ^{\hat{}} R˙RT=Φ^ ,
根据十四讲 4.8 的推导,最后则有 R ( t ) ˙ = Φ ^ ⋅ R ( t ) \dot{R(t)}=Φ^{\hat{}}·R(t) R(t)˙=Φ^⋅R(t)
这个李代数 Φ Φ Φ 反映了 R R R 的导数性质,所以李代数是李群 S O ( 3 ) SO(3) SO(3) 的正切空间,因为这里李群是9维的,所以切向量也是一个空间
李代数由一个方向和夹角构成, Φ = θ a , ∣ ∣ a ⃗ ∣ ∣ = 1 Φ=θa,||\vec{a}||=1 Φ=θa,∣∣a∣∣=1
指数映射,也是罗德里格斯公式
e x p ( Φ ∧ ) = e x p ( θ a ∧ ) = c o s θ I + ( 1 − c o s θ ) a a T + s i n θ a ∧ = R exp(Φ^{\wedge})=exp(θa^{\wedge})=cosθI+(1-cosθ)aa^{T}+sinθa^{\wedge}=R exp(Φ∧)=exp(θa∧)=cosθI+(1−cosθ)aaT+sinθa∧=R
e x p ( Φ ∧ ) = R exp(Φ^{\wedge})=R exp(Φ∧)=R
意思就是李代数 Φ Φ Φ 可以由角度 θ θ θ 和方向向量 a ⃗ \vec{a} a 表示,通过罗德里格斯公式可以变换成对应的旋转矩阵 S O ( 3 ) SO(3) SO(3)
用李代数表示旋转会有个问题,就是周期性,就是多个李代数可以对应一个旋转矩阵,如果固定旋转角度在±π时就是唯一对应的
由旋转矩阵 R R R 求李代数 Φ Φ Φ , θ = a r c c o s t r ( R ) − 1 2 , R a = a θ=arccos\frac{tr(R)-1}{2},Ra=a θ=arccos2tr(R)−1,Ra=a,由 l n ( R ) ∨ = Φ ln(R)^{\vee}=Φ ln(R)∨=Φ 表示
BCH一阶线性近似表达
l n ( e x p ( ϕ 1 ∧ ) e x p ( ϕ 2 ∧ ) ) ∨ ln(exp(\phi^{\wedge}_{1})exp(\phi^{\wedge}_{2}))^{\vee} ln(exp(ϕ1∧)exp(ϕ2∧))∨
当左边的 ϕ 1 \phi_{1} ϕ1 为小量时,此时相当于左乘,则
= > J l ( ϕ 2 ) − 1 ϕ 1 + ϕ 2 =>J_{l}(\phi_{2})^{-1}\phi_{1}+\phi_{2} =>Jl(ϕ2)−1ϕ1+ϕ2
其实就是相当于在 ϕ 2 \phi_{2} ϕ2 的基础上加上微量 J l ( ϕ 2 ) − 1 ϕ 1 J_{l}(\phi_{2})^{-1}\phi_{1} Jl(ϕ2)−1ϕ1
当右边的 ϕ 2 \phi_{2} ϕ2 为小量时,此时相当于右乘,则
= > J l ( ϕ 1 ) − 1 ϕ 2 + ϕ 1 =>J_{l}(\phi_{1})^{-1}\phi_{2}+\phi_{1} =>Jl(ϕ1)−1ϕ2+ϕ1
SLAM中我们构建了与位姿相关的函数后,需要讨论该函数对位姿的求导,以估计当前值
有两种方法求导
1、用李代数表示位姿,根据李代数加法对李代数求导
2、对李群进行左乘或右乘进行扰动,对扰动求导
由于使用李代数求导要计算 雅可比 J J J ,这个形式比较复杂,工程中不用这个方法,都是用扰动模型,所以只看扰动模型
∂ ( R p ) ∂ φ = l i m φ → 0 e x p ( φ ∧ ) e x p ( ϕ ∧ ) p − e x p ( ϕ ∧ ) p φ \frac{\partial(Rp)}{\partial\varphi}=lim_{\varphi\rightarrow0}\frac{exp(\varphi^{\wedge})exp(\phi^{\wedge})p-exp(\phi^{\wedge})p}{\varphi} ∂φ∂(Rp)=limφ→0φexp(φ∧)exp(ϕ∧)p−exp(ϕ∧)p
e x p ( φ ∧ ) exp(\varphi^{\wedge}) exp(φ∧) 是微量,相当于是对旋转的导数,则等于 ( I + φ ∧ ) (I+\varphi^{\wedge}) (I+φ∧)
具体推导如下
左乘扰动求导
这里是旋转 R R R 对向量 p p p 进行旋转,不停地左乘扰动来改变向量 p p p 的方向,左扰动 Δ R \Delta{R} ΔR 对应的李代数 φ \varphi φ , R p Rp Rp 的结果也是向量
∂ ( R p ) ∂ φ = l i m φ → 0 e x p ( φ ∧ ) e x p ( ϕ ∧ ) p − e x p ( ϕ ∧ ) p φ \frac{\partial(Rp)}{\partial\varphi}=lim_{\varphi\rightarrow0}\frac{exp(\varphi^{\wedge})exp(\phi^{\wedge})p-exp(\phi^{\wedge})p}{\varphi} ∂φ∂(Rp)=limφ→0φexp(φ∧)exp(ϕ∧)p−exp(ϕ∧)p
= l i m φ → 0 ( I + φ ∧ ) e x p ( ϕ ∧ ) p − e x p ( ϕ ∧ ) p φ =lim_{\varphi\rightarrow0}\frac{(I+\varphi^{\wedge})exp(\phi^{\wedge})p-exp(\phi^{\wedge})p}{\varphi} =limφ→0φ(I+φ∧)exp(ϕ∧)p−exp(ϕ∧)p
乘进去相减,很明显
= l i m φ → 0 φ ∧ R p φ =lim_{\varphi\rightarrow0}\frac{\varphi^{\wedge}Rp}{\varphi} =limφ→0φφ∧Rp
叉乘有一个性质, a ⃗ × b ⃗ = − b ⃗ × a ⃗ \vec{a}×\vec{b}=-\vec{b}×\vec{a} a×b=−b×a
a ⃗ × b ⃗ = a ∧ ⋅ b \vec{a}×\vec{b}=a^{\wedge}·b a×b=a∧⋅b
− b ⃗ × a ⃗ = − b ∧ ⋅ a -\vec{b}×\vec{a}=-b^{\wedge}·a −b×a=−b∧⋅a
则上式等于
= l i m φ → 0 − ( R p ) ∧ φ φ =lim_{\varphi\rightarrow0}\frac{-(Rp)^{\wedge}\varphi}{\varphi} =limφ→0φ−(Rp)∧φ
约掉 φ \varphi φ 则 l i m φ → 0 = − ( R p ) ∧ lim_{\varphi\rightarrow0}=-(Rp)^{\wedge} limφ→0=−(Rp)∧
这里省去了雅可比 J J J 的计算
对右乘也是一样的方法
矩阵转置的性质
( A + B ) T = A T + B T (A+B)^{T}=A^{T}+B^{T} (A+B)T=AT+BT
( λ A ) T = λ A T (\lambda{A})^{T}=\lambda{A^{T}} (λA)T=λAT
( A B ) T = B T A T (AB)^{T}=B^{T}A^{T} (AB)T=BTAT
SO(3)的伴随性质
R T E x p ( ϕ ) R = E x p ( R T ϕ ) R^{T}Exp(\phi)R=Exp(R^{T}\phi) RTExp(ϕ)R=Exp(RTϕ)
ϕ \phi ϕ 为扰动量 Δ R \Delta{R} ΔR 对应的李代数
对复合旋转进行求导
∂ L o g ( R 1 R 2 ) ∂ R 1 \frac{\partial Log(R_{1}R_{2})}{\partial R_{1}} ∂R1∂Log(R1R2)
这里是对两个相乘的旋转矩阵中的其中一个旋转进行求导,上面的左乘扰动例子是对矩阵相乘向量进行求导的,所以可以直接对矩阵进行扰动
但是这里不能直接对矩阵 S O ( 3 ) SO(3) SO(3) 进行扰动,不能直接说 R 1 R 2 R_{1}R_{2} R1R2 对 R 1 R_{1} R1 或 R 2 R_{2} R2 的导数,这样就变成矩阵对向量的求导,因为扰动量是可以用向量表示的,前面的例子 R p Rp Rp 相乘后也是个向量,所以可以直接对扰动量进行求导,但是这里两个矩阵相乘还是矩阵,所以得用 L o g Log Log 将矩阵相乘结果变为李代数,这样才符合求导的定义
L o g ( R ) = l o g ( R ) ∨ Log(R)=log(R)^{\vee} Log(R)=log(R)∨,用 L o g Log Log 就是为了懒得写 ∨ \vee ∨
对 R 1 R_{1} R1 进行右扰动
∂ L o g ( R 1 R 2 ) ∂ R 1 = l i m φ → 0 L o g ( R 1 E x p ( ϕ ) R 2 ) − L o g ( R 1 R 2 ) ϕ \frac{\partial Log(R_{1}R_{2})}{\partial R_{1}}=lim_{\varphi\rightarrow0}\frac{Log(R_{1}Exp(\phi)R_{2})-Log(R_{1}R_{2})}{\phi} ∂R1∂Log(R1R2)=limφ→0ϕLog(R1Exp(ϕ)R2)−Log(R1R2)
推导明天再写了
相关文章:

SLAM中求导相关的公式总结
李代数与李群的关系 R ˙ R T \dot{R}R^{T} R˙RT 是一个反对称矩阵,所以这个矩阵可以用一个13向量进行反对称来表示 R ˙ R T Φ ^ \dot{R}R^{T}Φ^{\hat{}} R˙RTΦ^ , 根据十四讲 4.8 的推导,最后则有 R ( t ) ˙ Φ ^ ⋅ R ( t ) \d…...
在微信小程序中怎么做投票活动
在当今社交媒体时代,微信小程序已经成为一种广泛使用的互动营销工具。通过各种活动,企业可以吸引用户的关注,提升品牌影响力。其中,投票活动是一种特别受欢迎的形式。本文将为你详细介绍如何在微信小程序中创建投票活动。 一、微信…...
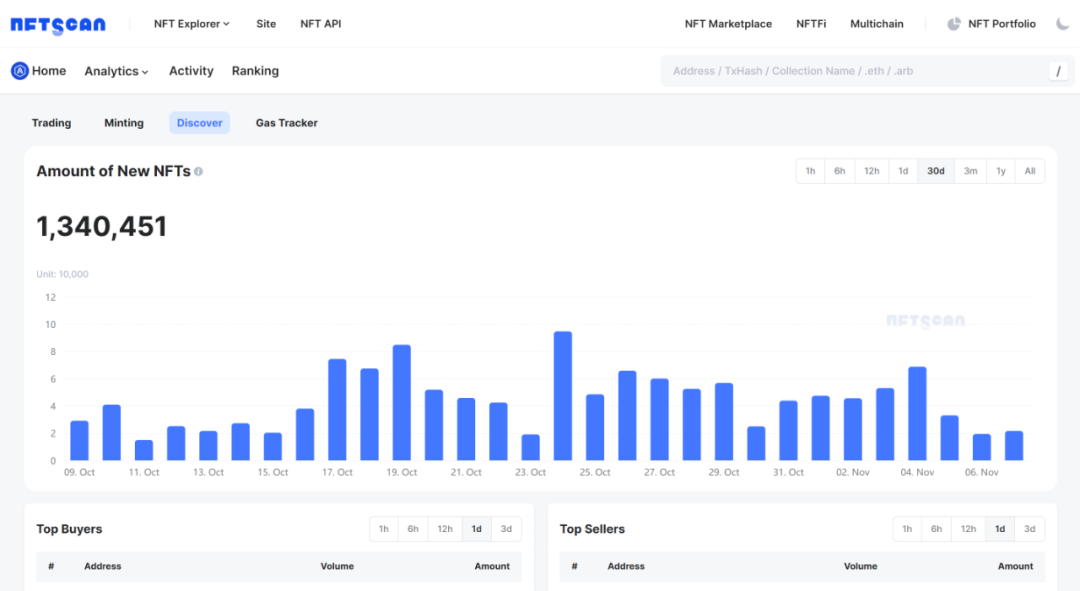
如何使用 NFTScan NFT API 在 Arbitrum 网络上开发 Web3 应用
Arbitrum 是以太坊的 Layer 2 扩容方案,为以太坊面临的高 gas 费和网络拥堵问题,提供了一个解决方案。作为 Layer 1 的以太坊基础层受每秒只能验算 15 笔交易的限制,在目前以太坊使用需求庞大的情况下,局限了以太坊的可扩展性。Ar…...
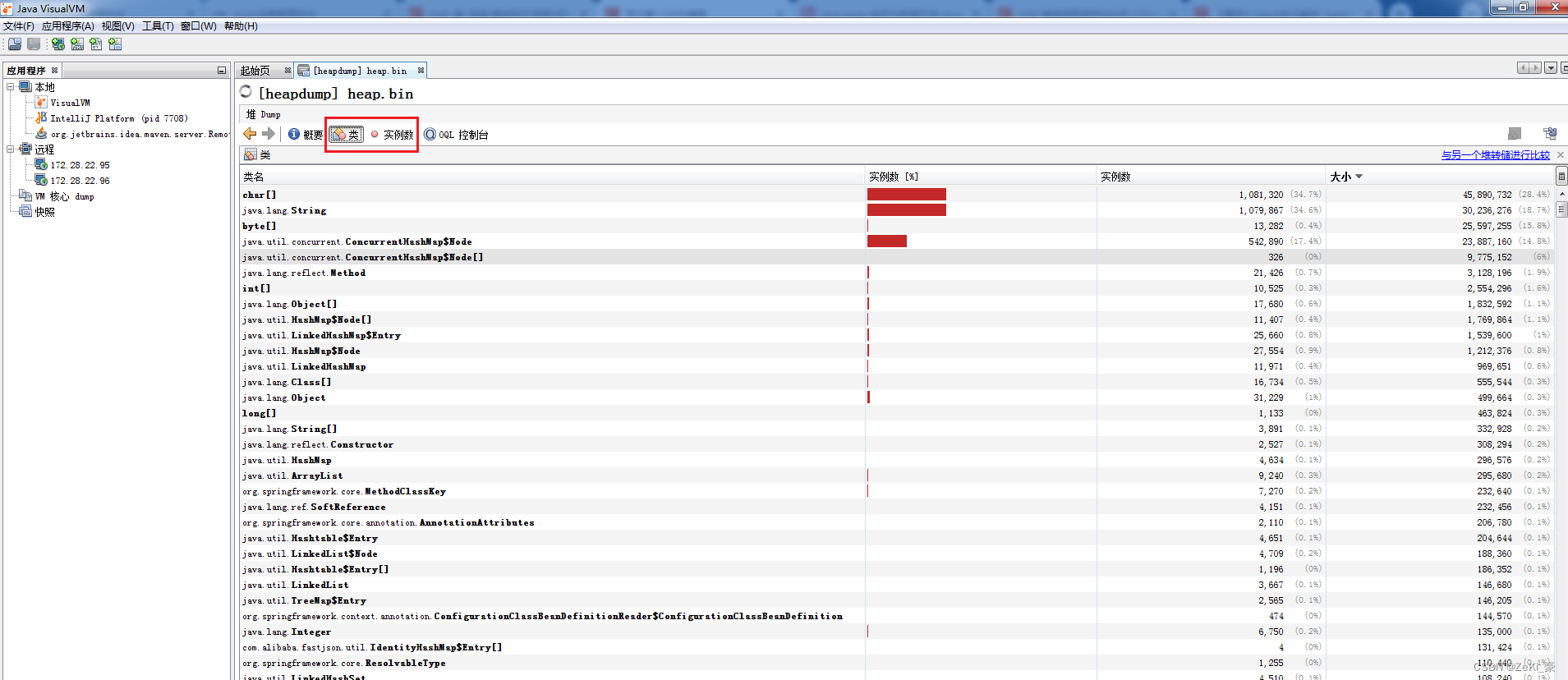
线上问题排查方法
查看栈信息 先进入docker容器,docker exec -it 容器号 bash *查看线程占用排行top -Hp 1,此处PID为线程号 查看各线程情况jstack -l 1 可以将栈信息生成文件jstack -l 1 > 2.log 查看对应线程号的信息,比如要看线程号PID是28的,那么28的16进制是1C,则检索栈文件里ox1…...

智能柜+MRO:制造业中的自动售货机
每当谈及企业数字化转型,多数人想到的是人工智能、大数据等高端技术的应用,或是原有业务流程和运营方式的数字化与自动化,实现大幅降本增效等。然而,对于急需在数字时代找到生存之道的企业来说,数字化转型的要求远不止…...

flutter笔记:骨架化加载器
flutter笔记 骨架化加载器 - 文章信息 - Author: Jack Lee (jcLee95) Visit me at: https://jclee95.blog.csdn.netEmail: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/qq_28550263/article/details/134224135 【介绍】:本文介…...

关于视频封装格式和视频编码格式的简介
文章目录 简介视频封装格式(Video Container Format)视频编码格式(Video Compression Format)两者关系总结webm 格式简介webm视频编码格式webm音频编码格式webm总结 简介 视频封装格式(Video Container Format&#x…...
npm发布自己的包
npm发布自己的包 1. 首先在npm官网注册一个自己的账户(有账号的可以直接登录) 注册地址 2. 创建一个自己的项目(如果已有自己的项目, 跳过这一步) npm init -y3. 确认自己的npm下载源, 只能使用npm官方的地址 npm config get registry修改地址源 npm config set registr…...
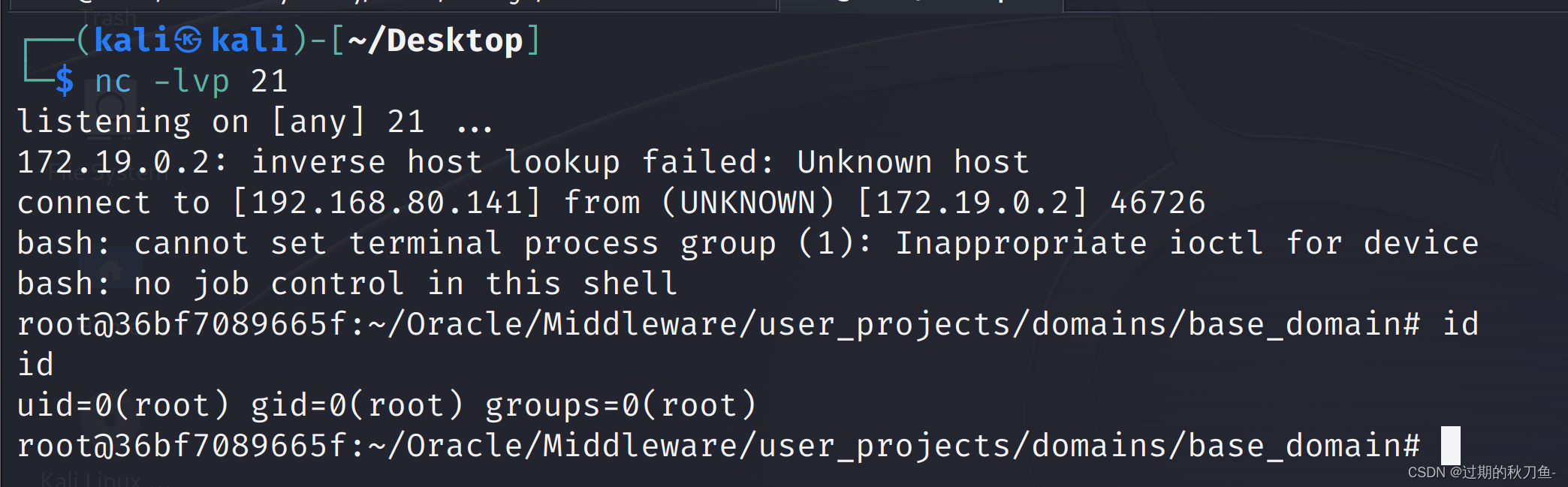
【漏洞复现】weblogic-10.3.6-‘wls-wsat‘-XMLDecoder反序列化(CVE-2017-10271)
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现1、基础环境2、漏洞扫描nacsweblogicScanner3、漏洞验证 说明内容漏洞编号CVE-2017-10271漏洞名称Weblogic < 10.3.…...

CRM中的销售机会管理是什么?三个步骤帮你创建销售渠道
企业销售业务中,有个名词叫做“机会管理”,有效的机会管理可以帮助销售人员准确地抓住潜在客户群体,并将其转化为真正的客户、持续带来收入。CRM客户管理系统也是销售机会管理的一个重要工具,帮助销售人员与正确的人建立起关系&am…...
怎么发推文最有效?技巧分享)
X(原Twitter)怎么发推文最有效?技巧分享
随着人们对于TikTok和INS 等社交媒体平台的热情不断高涨,可能渐渐忽视了X(原Twitter)这一不可或缺的海外社交媒体巨头。尽管 X(原Twitter)并未放弃其以280个字符的推文为核心的社交模式,但是众多流行文化和…...
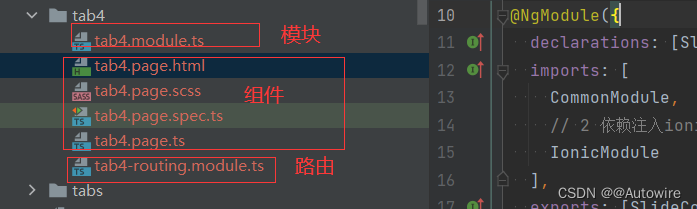
Ionic 模块组件的理解
1 Ionic4.x 文件分析 1.1 app.module.ts 分析 Ionic 是一个基于 Angular 的移动应用开发框架,能帮助开发者使用 Web 技术(HTML5、CSS3、JavaScript)创建跨平台的应用程序。在 Ionic 应用程序中,app.module.ts 文件是整个应用程序的…...

sql:1对多获取最新一条数据
假设A表为table_a,B表为table_b,它们之间通过主键ID关联。我们可以利用窗口函数ROW_NUMBER()来获取B表中每条A记录对应的最新一条B记录。以下是SQL语句: SELECT a.*,b.* FROM table_a a LEFT JOIN (SELECT *,ROW_NUMBER() OVER (PARTITION B…...

CDN加速技术:降低企业云服务成本的有效利用
在当今数字化时代,云服务已经成为企业运营的不可或缺的一部分。然而,与此同时,云服务的需求也在不断增长,使企业不得不应对更大的数据传输和负载。这就引出了一个关键问题:如何有效降低企业云服务成本,同时…...
+ Spring相关源码)
设计模式——享元模式(Flyweight Pattern)+ Spring相关源码
文章目录 一、享元模式定义二、例子2.1 菜鸟教程例子2.1.1 定义被缓存对象2.1.2 定义ShapeFactory 2.2 JDK源码——Integer2.3 JDK源码——DriverManager2.4 Spring源码——HandlerMethodArgumentResolverComposite除此之外BeanFactory获取bean其实也是一种享元模式的应用。 三…...

vue3中el-tree设置默认选中节点和展开节点
1.el-tree设置 node-key,current-node-key,default-expanded-keys,highlight-current: <el-tree ref"taskTree" :data"ptreeData" node-key"key" :current-node-key"currentKey" …...

软件测试需求分析是什么?为什么需要进行测试需求分析?
在软件开发中,软件测试是确保软件质量的重要环节之一。而软件测试需求分析作为软件测试的前置工作,对于保证软件测试的顺利进行具有重要意义。软件测试需求分析是指对软件测试的需求进行细致的分析和规划,以明确测试的目标、任务和范围&#…...

GreenPlum简介
简介 Greenplum是一家总部位于**美国加利福尼亚州,为全球大型企业用户提供新型企业级数据仓库(EDW)、企业级数据云(EDC)和商务智能(BI)提供解决方案和咨询服务的公司,在全球已有:纳斯达克,纽约证券交易所,Skype. FOX&…...

HTML和CSS入门学习
目录 一.HTML 二.CSS 1.CSS作用:美化页面 2.CSS语法 【1】CSS语法规范 【2】如何插入样式表 3.CSS选择器 4.CSS设置样式属性--设置html各种标签的属性 【1】文本属性--设置整段文字的样式 【2】字体属性--设置单个字的样式 【3】链接属性--设置链接的样式…...
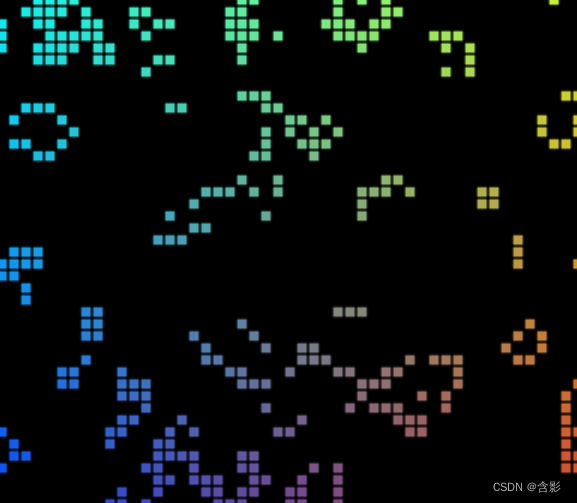
轻量封装WebGPU渲染系统示例<17>- 使用GPU Compute之元胞自动机(源码)
注: 此示例通过渲染实体的渲染过程控制来实现。此实现方式繁琐,这里用于说明相关用法。 更简洁的实现请见: 轻量封装WebGPU渲染系统示例<19>- 使用GPU Compute材质多pass元胞自动机(源码)-CSDN博客 当前示例源码github地址: ht…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...
