数据可视化PCA与t-SNE
PCA(主成分分析)和t-SNE(t分布随机近邻嵌入)都是降维技术,可以用于数据的可视化和特征提取。
降维:把数据或特征的维数降低,其基本作用包括:
- 提高样本密度,以及使基于欧氏距离的算法重新生效
- 数据预处理。对数据去冗余、降低信噪比
- 方便可视化
降维主要可以分为线性降维和非线性降维
- 线性降维
- 侧重让不相似的点在低维表示中分开
- MDS(Multiple Dimensional Scaling,多维缩放)
- PCA(Principle Components Analysis,主成分分析)
- 非线性降维
- 非线性降维中用到的方法大多属于流形学习方法
- 这类技术假设高维数据实际上处于一个比所处空间维度低的非线性流形上,因此侧重让相似的近邻点在低维表示中靠近
- Sammon mapping
- SNE(Stochastic Neighbor Embedding,随机近邻嵌入),t-SNE是基于SNE的
- Isomap(Isometric Mapping,等度量映射)
- MVU(Maximum Variance Unfolding)
- LLE(Locally Linear Embedding,局部线性嵌入)等
1.PCA
1.1. PCA的原理
主成分分析(Principal Component Analysis,PCA)是一种常用的数据降维方法,它通过将原始数据投影到一个新的坐标系中,将数据中的冗余信息消除,并保留最有用的信息。具体来说,PCA会找到数据中的主成分,将数据沿着主成分方向进行旋转,使得旋转后的数据方差最大。这样可以有效减少数据的维度,从而降低模型复杂度,避免过拟合。
假设我们有一个数据集X={x1,x2,...,xn},其中 ,我们的目标是将数据从 d维降至 k维 (k<d)。PCA 的基本思想是找到一个正交基,使得数据在这组基上的投影方差最大。具体来说,我们可以按照以下步骤进行 PCA:
- 对数据进行中心化处理,即对每个维度减去该维度上的均值,使得数据的均值为 0。
- 计算协方差矩阵 C,其中
表示 x 在第 i 个维度和第 j个维度上的协方差。
- 对协方差矩阵进行特征值分解,得到特征值
和对应的特征向量
。其中,特征向量表示数据在第 i 个维度上的投影方向。
- 选择前 k 个特征值对应的特征向量
,将原始数据投影到这组基上。
下面是 PCA 的数学公式:
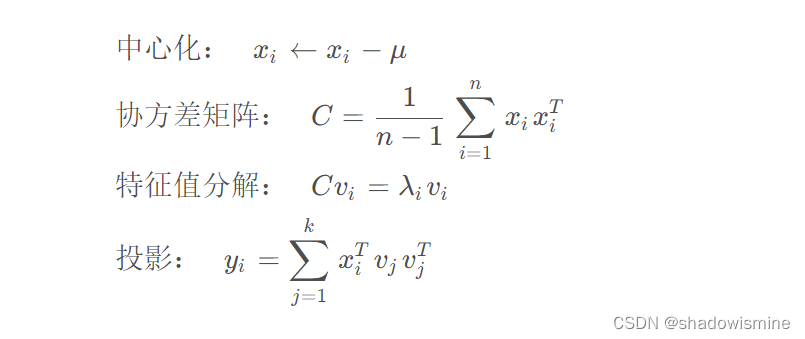
1.2. PCA的实现
在实现PCA算法时,我们需要执行以下步骤:
- 将数据集进行标准化,使得每个特征的均值为0,方差为1。这可以通过对每个特征减去其均值并除以其标准差来实现。
- 计算数据的协方差矩阵。
- 对协方差矩阵进行特征值分解。
- 选择前k个特征值对应的特征向量作为新的基向量。
- 将原始数据投影到新的低维空间中。
在Python中,我们可以使用NumPy和SciPy库来实现PCA算法。以下是一个简单的示例代码,演示如何使用Python和NumPy实现PCA算法:
import numpy as npdef pca(X, k):# 标准化数据X_std = (X - np.mean(X, axis=0)) / np.std(X, axis=0)# 计算协方差矩阵cov_mat = np.cov(X_std, rowvar=False)# 特征值分解eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)# 选择前k个特征值对应的特征向量eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]eigen_pairs.sort(reverse=True, key=lambda k: k[0])w = np.hstack([eigen_pairs[i][1].reshape(-1, 1) for i in range(k)])# 将原始数据投影到新的低维空间中X_pca = X_std.dot(w)return X_pca
在上面的代码中,我们使用numpy.cov()函数计算数据的协方差矩阵,使用numpy.linalg.eig()函数进行特征值分解,然后选择前k个特征值对应的特征向量。最后,我们将原始数据投影到新的低维空间中。
1.3 数据可视化
PCA可以将高维数据映射到二维或三维空间中,从而实现数据的可视化。这种可视化方式通常被称为“主成分分析图”或“PCA图”。下面我们以手写数字数据集为例,演示如何利用PCA进行数据可视化。
首先加载手写数字数据集:
from sklearn.datasets import load_digitsdigits = load_digits()
X = digits.data
y = digits.target
然后我们对数据进行PCA降维:
from sklearn.decomposition import PCApca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
最后,我们将数据可视化:
import matplotlib.pyplot as pltplt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, alpha=0.5)
plt.colorbar()
plt.show()
运行上述代码后,我们可以得到一个二维的PCA图,其中不同颜色的点代表不同的手写数字,如下图所示:

这个图显示了手写数字数据集的PCA可视化结果。在这个二维图中,我们可以看到不同的数字在不同的区域内形成了簇。例如,数字0、6和1在左上角的区域内形成了簇,数字3、8和9在右下角的区域内形成了簇,数字2和7分别位于两个簇的中间位置。
PCA除了可以做数据可视化,也可以对数据进行降维操作。如在图像处理领域,我们常常需要将高维的像素点转化为低维的向量,以便于更好地进行图像分类、压缩等操作。使用PCA对图像进行降维处理是一种常见的方法。以人脸识别为例,我们可以使用PCA对人脸图像进行降维处理,将每张人脸图像转化为一个低维向量,然后使用这些向量进行人脸识别。
除此之外,PCA还可以做数据压缩和去噪。
2. t-SNE
t-SNE(t-Distributed Stochastic Neighbor Embedding)是一种非线性降维算法,用于将高维数据映射到低维空间。与PCA不同,t-SNE旨在保留数据点之间的局部关系,并在低维空间中反映这种关系,而不是仅仅保留方差最大的维度。它的主要思想是在高维空间中计算数据点之间的相似度,然后在低维空间中将这些相似度转换为概率分布,从而最小化原始空间和低维空间之间的KL散度(Kullback-Leibler Divergence)。
具体来说,对于每个数据点i,t-SNE首先计算它与其他数据点j之间的相似度 ,并利用高斯分布函数转换为概率分布
,表示如果在低维空间中,点i选择点j作为邻居点的概率。在低维空间中,每个点k被表示为
的概率分布,表示如果在高维空间中,点i选择点j作为邻居点的概率。t-SNE通过最小化
和
之间的KL散度来优化这些概率分布,从而将高维数据映射到低维空间。
Python中有多个库可以实现t-SNE算法
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, perplexity=30.0, early_exaggeration=12.0, learning_rate=200.0)
X_tsne = tsne.fit_transform(X)
其中,n_components指定了降维后的维度数,perplexity是t-SNE算法中的一个超参数,用于控制每个点周围的邻居数量,early_exaggeration是控制t-SNE计算过程中的簇大小的参数,learning_rate是学习率,控制梯度下降的步长。
2.1 t-SNE的应用
t-SNE主要用于可视化高维数据,特别是当我们想要探索数据中的局部结构时。例如,在自然语言处理中,我们可以使用t-SNE来可视化单词嵌入,以了解单词之间的语义关系。在图像处理中,t-SNE可以用于可视化图像的特征向量,以探索图像之间的相似性。
2.1.1 图像处理
t-SNE也可以用于图像处理中的特征提取和图像聚类。在这种情况下,我们可以使用卷积神经网络(CNN)提取图像特征,并使用t-SNE对这些特征进行降维,然后进行聚类或可视化。
例如,我们可以使用一个预先训练好的CNN模型,如VGG或ResNet,对图像进行特征提取。然后,我们可以使用t-SNE将这些高维特征降到二维或三维,以便进行可视化或聚类。
以下是一个使用t-SNE可视化MNIST数据集的示例:
import numpy as np
from sklearn.manifold import TSNE
from sklearn.datasets import fetch_openml
import matplotlib.pyplot as plt# 获取MNIST数据集
mnist = fetch_openml('mnist_784')
X, y = mnist.data / 255.0, mnist.target# 使用预训练的卷积神经网络(CNN)提取特征
# ...# 使用t-SNE降维
tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X_features)# 可视化降维后的数据
plt.figure(figsize=(10, 10))
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y.astype(int), cmap='jet')
plt.axis('off')
plt.colorbar()
plt.show()
该代码使用MNIST数据集作为示例数据集。首先,我们通过fetch_openml函数获取MNIST数据集,并对像素值进行归一化。然后,我们使用预训练的CNN模型提取图像的特征。最后,我们使用t-SNE将这些特征降至二维,并将结果可视化。
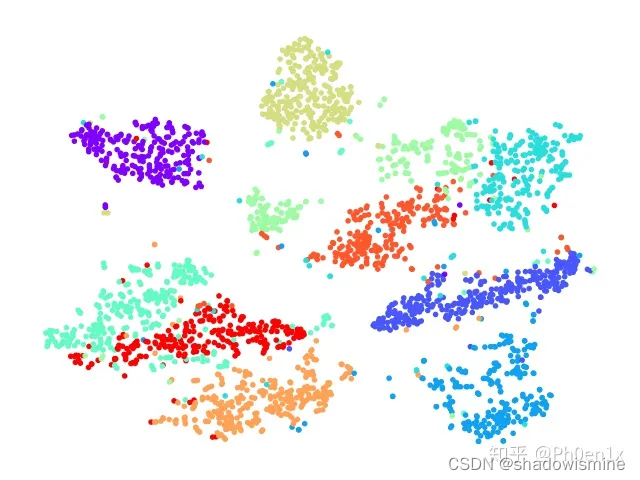
2.1.2 自然语言处理
t-SNE 在自然语言处理中也有广泛的应用,特别是在词向量的可视化方面。在自然语言处理中,我们经常使用词向量来表示单词。词向量是将每个单词表示为一个向量,使得每个向量都能够捕捉到该单词的语义信息。词向量通常在高维空间中表示,其中每个维度对应于单词的某个特定特征。
使用 t-SNE 可以将高维词向量降至 2 维或 3 维,然后使用二维或三维散点图将它们可视化。通过这种方式,我们可以更好地理解单词之间的相似性,例如,在这些可视化中,词向量非常相似的单词将在二维或三维空间中彼此靠近。
from sklearn.manifold import TSNE
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
import matplotlib.pyplot as plt# 加载新闻数据集
newsgroups = fetch_20newsgroups(subset='all',categories=['alt.atheism', 'comp.graphics','comp.os.ms-windows.misc', 'comp.sys.ibm.pc.hardware','comp.sys.mac.hardware', 'comp.windows.x', 'misc.forsale','rec.autos', 'rec.motorcycles', 'rec.sport.baseball','rec.sport.hockey', 'sci.crypt', 'sci.electronics','sci.med', 'sci.space', 'soc.religion.christian', 'talk.politics.guns','talk.politics.mideast', 'talk.politics.misc', 'talk.religion.misc'])# 抽取词频特征
vectorizer = CountVectorizer(stop_words='english')
X = vectorizer.fit_transform(newsgroups.data)# 使用t-SNE进行降维
tsne = TSNE(n_components=2, verbose=1, perplexity=40, n_iter=300)
X_tsne = tsne.fit_transform(X.toarray())# 将降维结果可视化
plt.scatter(X_tsne[:, 0], X_tsne[:, 1])
plt.show()
运行上述代码后,我们可以得到一个散点图,其中每个点代表一个单词,相似的单词会被放置在相似的位置,这有助于我们更好地理解单词之间的语义关系。
需要注意的是,对于大型数据集,t-SNE 可能需要很长时间才能完成降维。在这种情况下,可以尝试使用随机子采样来减少数据点数量。
3. 如何选择PCA还是t-SNE
在选择PCA或t-SNE时,需要考虑以下几个因素:
数据类型:如果数据是高维稠密的,那么PCA是一个更好的选择,因为t-SNE需要大量的计算资源来处理大规模数据。如果数据是低维或稀疏的,t-SNE是更好的选择。
目标:如果目标是可视化数据集并检查其聚类结构或在二维或三维空间中查看数据点的分布,t-SNE是更好的选择。如果目标是减少数据的维度以进行机器学习或其他应用,PCA是更好的选择。
计算资源:PCA是一个快速而直接的方法,而t-SNE需要更多的计算资源和时间。如果计算资源有限,PCA是更好的选择。
参考:https://blog.csdn.net/qq_33578950/article/details/130042918
相关文章:

数据可视化PCA与t-SNE
PCA(主成分分析)和t-SNE(t分布随机近邻嵌入)都是降维技术,可以用于数据的可视化和特征提取。 降维:把数据或特征的维数降低,其基本作用包括: 提高样本密度,以及使基于欧…...

Kubernetes rancher、prometheus、ELK的安装
目录 一、rancher的安装1. 添加 Helm Chart 仓库2. 为 Rancher 创建命名空间3. 选择 SSL 配置4. 安装 cert-manager 二、prometheus安装三、EFK安装3.1安装elasticsearch3.2安装filebeat3.3安装kibana 一、rancher的安装 有关rancher的安装其实官方网站给的步骤已经很详细了&a…...
为什么我们要努力的学习编程?初学编程从哪里开始学起?
为什么我们要努力的学习编程?初学编程从哪里开始学起? 1、不论在哪里上班,都不是铁饭碗:现在全球经济低迷,使得很多企业倒闭,大到知名国企小到私营企业,大量裁员。任何人都无法保证自己现在的工…...
)
ffmpeg 从内存中读取数据(或将数据输出到内存)
1.为了使本文更通俗易懂,更新了部分内容,将例子改为从内存中打开。 2.增加了将数据输出到内存的方法。 从内存中读取数据 ffmpeg一般情况下支持打开一个本地文件,例如“C:\test.avi” 或者是一个流媒体协议的URL,例如“rtmp:/…...
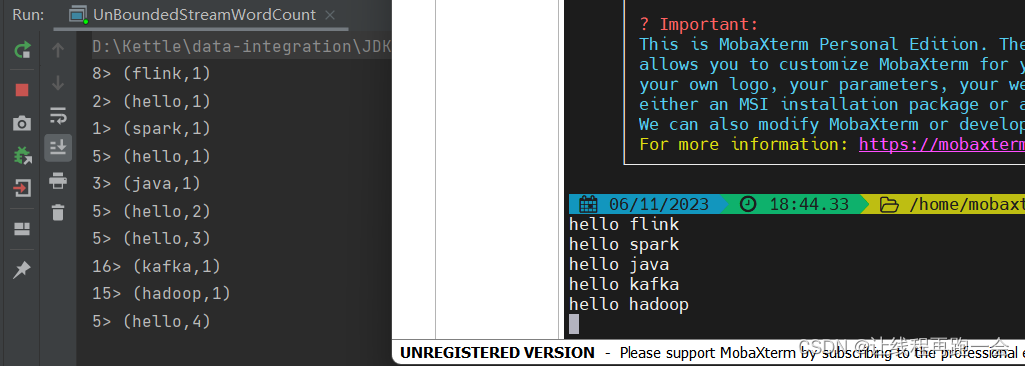
Flink(一)【WordCount 快速入门】
前言 学完了 Hadoop、Spark,本想着先把 Kafka、Flume 这些工具先学完的,但想了想还是把核心的技术先学完最后再去把那些工具学学。 最近心有点累哈哈哈,偷偷立个 flag,反正也没人看,明年的今天来这里还愿哈,…...

【Redis】hash数据类型-常用命令
文章目录 前置知识常用命令HSETHGETHEXISTSHDELHKEYSHVALSHGETALLHMGET关于HMSETHLENHSETNXHINCRBYHINCRBYFLOAT 命令小结 前置知识 redis自身就是键值对结构了,哈希类型是指值本⾝⼜是⼀个键值对结构,形如key"key",value{{field1…...

【大数据】Apache NiFi 数据同步流程实践
Apache NiFi 数据同步流程实践 1.环境2.Apache NIFI 部署2.1 获取安装包2.2 部署 Apache NIFI 3.NIFI 在手,跟我走!3.1 准备表结构和数据3.2 新建一个 Process Group3.3 新建一个 GenerateTableFetch 组件3.4 配置 GenerateTableFetch 组件3.5 配置 DBCP…...
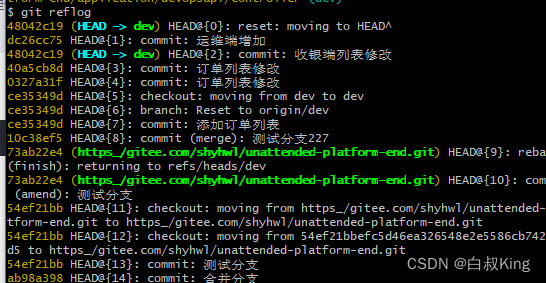
git怎么使用 拉取代码
废话不多说 直接开干 Git 是一款十分实用的版本控制工具,非常方便地管理代码的变更。但是,在使用 Git 过程中,不可避免地会遇到一些问题。其中,删除分支是一个常见的问题。 查看引用历史记录: git reflog找到你删除的…...

Apple :苹果将在明年年底推出自己的 AI,预计将随 iOS 18 一起推出
本心、输入输出、结果 文章目录 Apple :苹果将在明年年底推出自己的 AI,预计将随 iOS 18 一起推出前言三星声称库克相关图片弘扬爱国精神 Apple :苹果将在明年年底推出自己的 AI,预计将随 iOS 18 一起推出 编辑:简简单…...
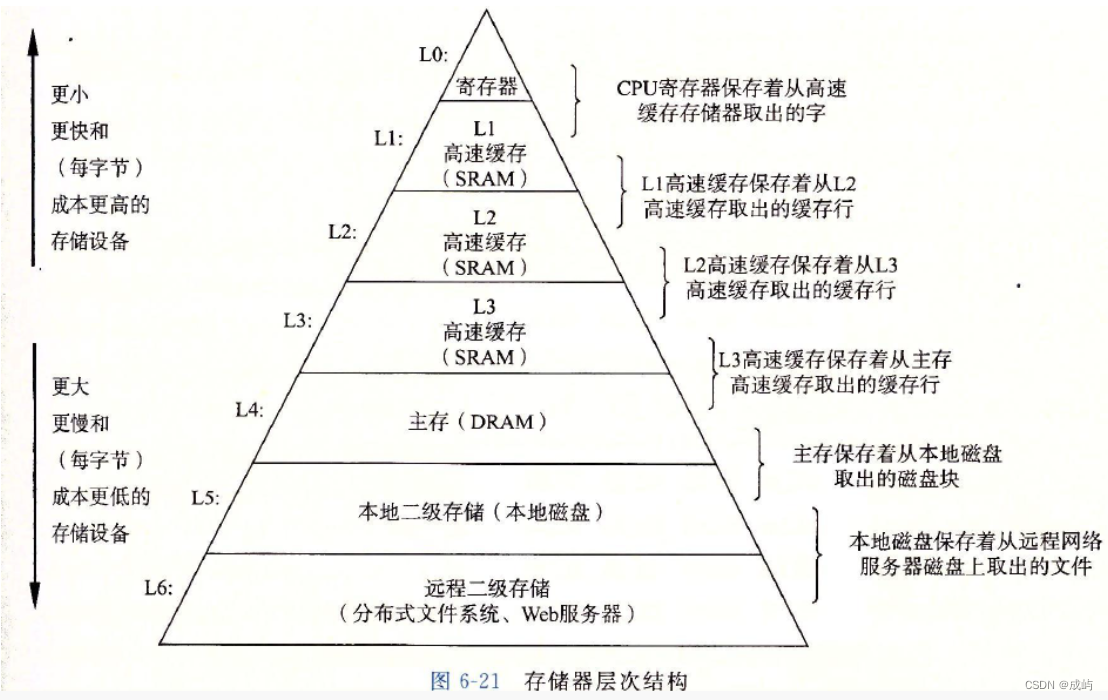
数据结构-双向链表
1.带头双向循环链表: 前面我们已经知道了链表的结构有8种,我们主要学习下面两种: 前面我们已经学习了无头单向非循环链表,今天我们来学习带头双向循环链表: 带头双向循环链表:结构最复杂,一般用…...
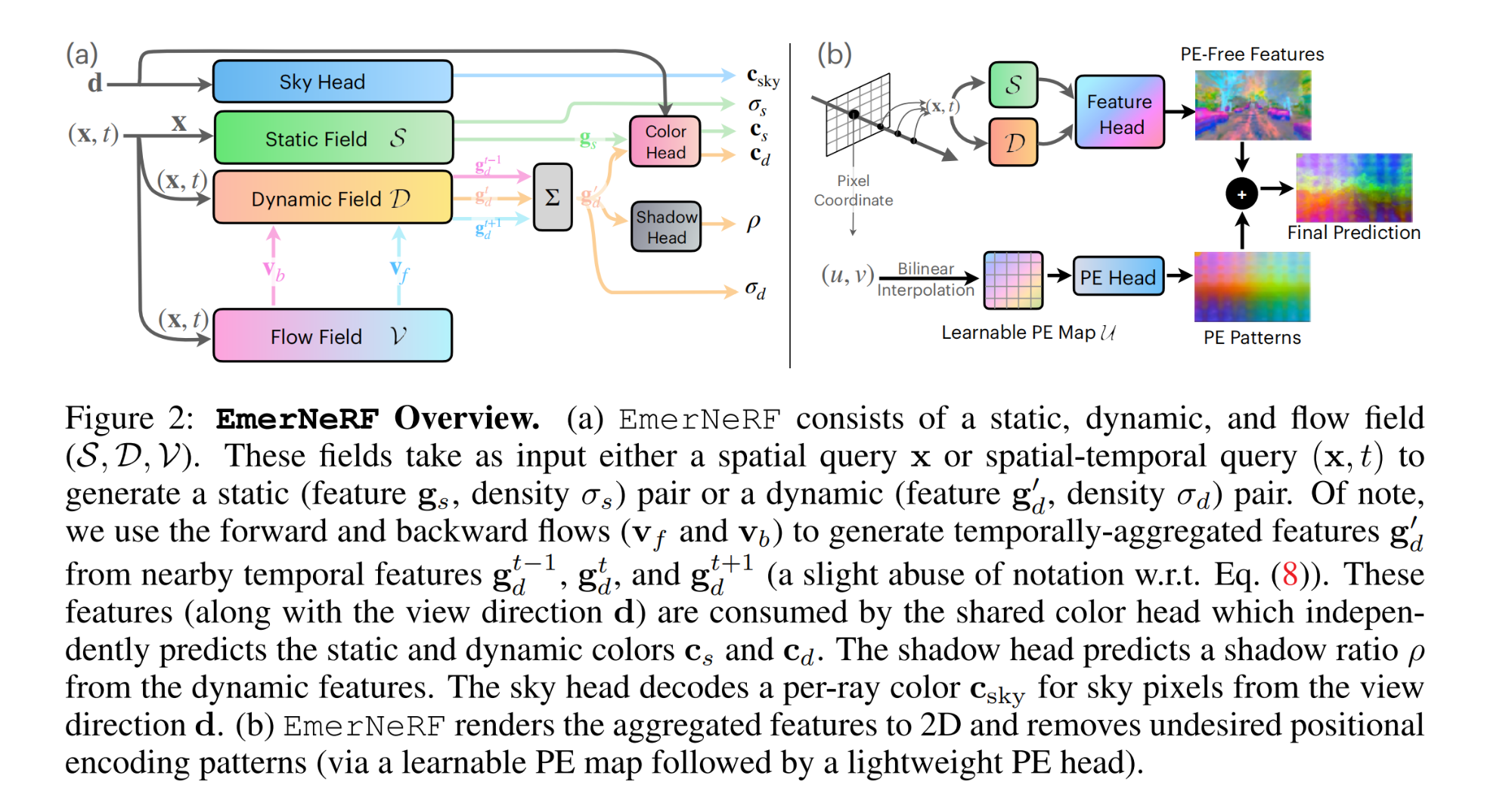
CV计算机视觉每日开源代码Paper with code速览-2023.11.6
精华置顶 墙裂推荐!小白如何1个月系统学习CV核心知识:链接 点击CV计算机视觉,关注更多CV干货 论文已打包,点击进入—>下载界面 点击加入—>CV计算机视觉交流群 1.【点云3D目标检测】(NeurIPS2023)…...

GB28181学习(十五)——流传输方式
前言 基于GB/T28181-2022版本,实时流的传输方式包括3种: UDPTCP被动TCP主动 UDP 流程 注意: m字段指定传输方式为RTP/AVP; 抓包 SIP服务器发送INVITE请求; INVITE sip:xxx192.168.0.111:5060 SIP/2.0 Via: SIP…...

【Linux】:初识git || centos下安装git || 创建本地仓库 || 配置本地仓库 || 认识工作区/暂存区(索引)以及版本库
📮1.初识git Git 原理与使用 课程⽬标 • 技术⽬标:掌握Git企业级应⽤,深刻理解Git操作过程与操作原理,理解⼯作区,暂存区,版本库的含义 • 技术⽬标:掌握Git版本管理,⾃由进⾏版本回退、撤销、修改等Git操…...

Vue 3 中,watch 和 watchEffect 的区别
结论先行: watch 和 watchEffect 都是监听器,都是用来监听响应式数据的变化并执行相应操作。区别是: watch:需要指明要监听的数据,而且在回调函数中可以获取到属性变化的前后值; 适用于需要精确控制监视…...
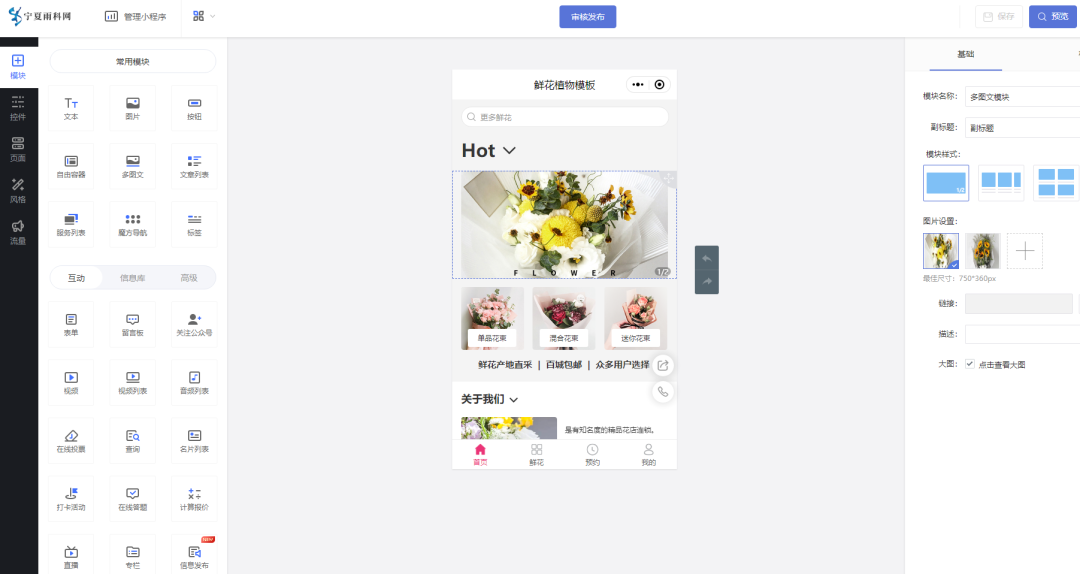
鲜花展示服务预约小程序的效果如何
鲜花产品的市场需求度非常高,互联网深入各个行业,很多鲜花商家都会通过线上建立平台实现产品销售、获客引流、转化复购、生意增长等,当然除了搭建鲜花商城小程序外,对鲜花供应商及门店还有展示预约方面的需求。 通过【雨科】平台可…...

Linux下多个盘符乱的问题处理
参考文档: linux下man fstab命令查看帮助,有一段说明,可以使用UUID,或者LABEL 来绑定盘。这里使用UUID来绑定 Instead of giving the device explicitly, one may indicate the filesystem that is to be mounted by its UUID …...

uniapp小程序使用web-view组件页面分享后,点击没有home小房子解决办法
uniapp小程序使用web-view组件页面分享后,点击没有home小房子解决办法 小程序 :IOS 测试正常, 安卓 不显示home 微信小程序使用的是全局自定义导航,通过首页 banner 跳转到一个 web-view 页面,展示官网。 web-view 页…...

SLAM_语义SLAM相关论文
目录 1. 综述 2. 相关文章 Probabilistic Data Association for Semantic SLAM VSO:Visual Semantic Odometry 语义信息分割运动物体...

【技巧】并发读取Mysql数据保证读取到的数据不重复
【技巧】并发读取Mysql数据保证读取到的数据不重复 使用场景: 并发场景下, 保证不获取到重复的数据 思路: 先通过 MYSQL锁 去占位打标识,然后再去取数据 相当于几个人抢蛋糕, A先把蛋糕打上记号 蛋糕是A的, 然后再慢慢吃 表结构 表 t_userid name val used_flag 是否使用…...

Lavarel异步队列的使用
系统为window 启动队列: php artisan queue:listen设置队列类 .env文件需设置:QUEUE_CONNECTIONredis <?phpnamespace App\Jobs;use Illuminate\Bus\Queueable; use Illuminate\Contracts\Queue\ShouldQueue; use Illuminate\Foundation\Bus\Disp…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
