R语言中的函数26:polyroot多项式求根函数
目录
- 介绍
- 函数介绍
- 参数含义
- 示例
介绍
R语言中的base::polyroot()可以用于对多项式求根,求根的多项式可以是复数域上的。
函数介绍
polyroot(z)
该函数利用Jenkins-Traub算法对多项式 p ( x ) p(x) p(x)进行求根,其中
p ( x ) = z 1 + z 2 x + ⋯ + z n x n − 1 p(x)=z_1+z_2x+\cdots+z_n x^{n-1} p(x)=z1+z2x+⋯+znxn−1
参数含义
- z: 是一个多项式系数组成的向量,多项式按照各项次数的升序排列
示例
求解多项式 p ( x ) p(x) p(x)的根,其表达式为:
p ( x ) = 2 + 3 x 2 − x 3 + 7 x 4 p(x)=2+3x^2-x^3+7x^4 p(x)=2+3x2−x3+7x4
> polyroot(z=c(2,0,3,-1,7))
# [1] 0.4387643+0.6258357i
# [2] -0.3673358+0.5951023i
# [3] -0.3673358-0.5951023i
# [4] 0.4387643-0.6258357i
相关文章:

R语言中的函数26:polyroot多项式求根函数
目录 介绍函数介绍参数含义 示例 介绍 R语言中的base::polyroot()可以用于对多项式求根,求根的多项式可以是复数域上的。 函数介绍 polyroot(z)该函数利用Jenkins-Traub算法对多项式 p ( x ) p(x) p(x)进行求根,其中 p ( x ) z 1 z 2 x ⋯ z n x…...

2023年辽宁省数学建模竞赛A题铁路车站的安全标线
2023年辽宁省数学建模竞赛 A题 铁路车站的安全标线 原题再现: 在火车站或地铁站台上,离站台边缘 1 米左右的地方都画有一条黄线(或白线),这是为什么呢? 这条线称为安全线(业内称之为安全标线),人们在候车时必须站在安全线以…...

半导体工厂将应用哪些制造创新技术?
半导体工厂是高科技产业的结晶,汇聚了世界上最新的技术。 在半导体的原料硅晶片上绘制设计图纸,不产生误差,准确切割并包装,然后用芯片生产出我们使用的电脑、智能手机、手表等各种电子产品。绝大多数半导体厂都采用一贯的工艺&a…...
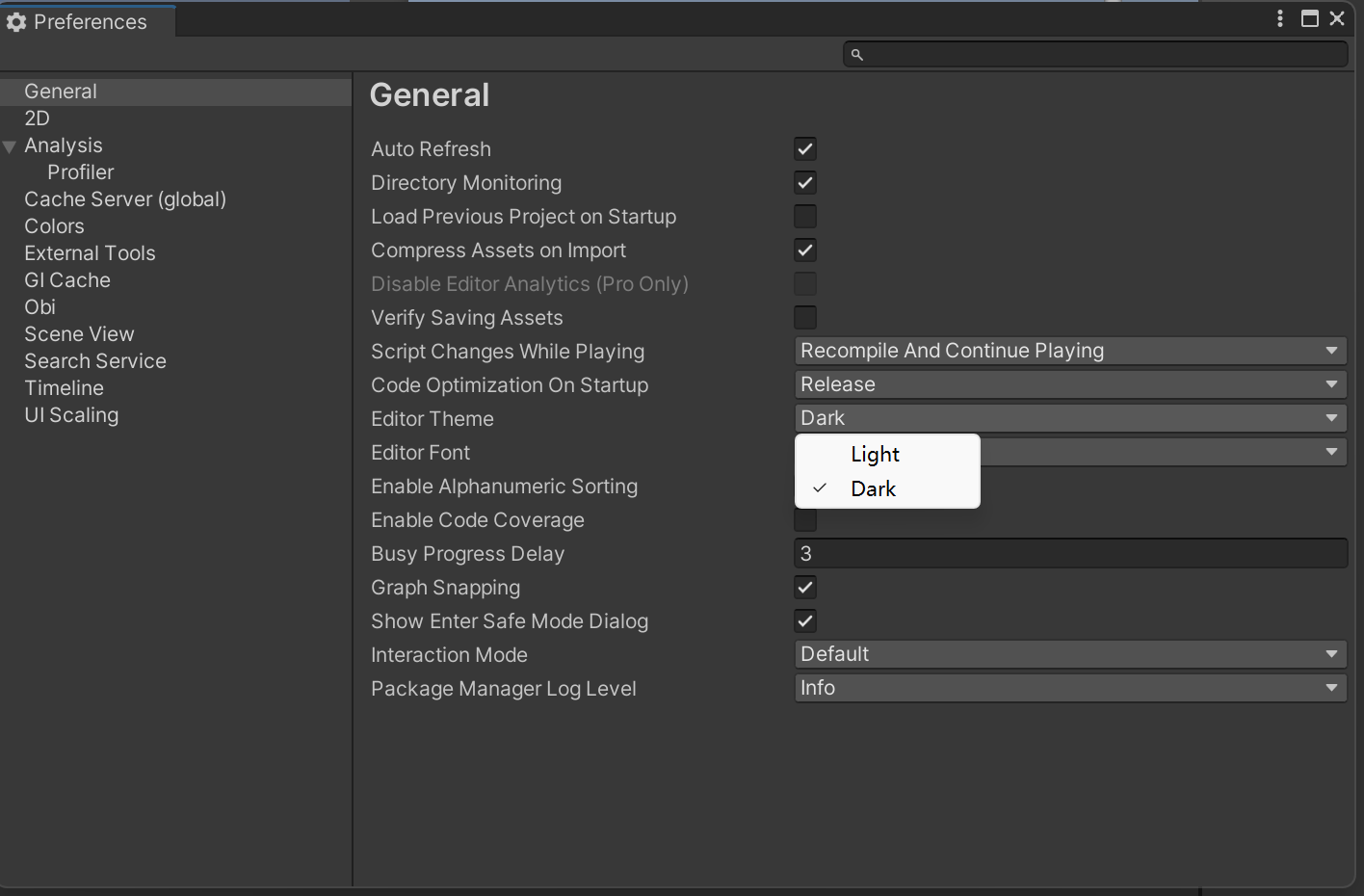
[unity]深色模式/浅色模式
这里用的是Windows版的unity,具体版本号如下: 选项的路径如下:Edit—Preferences—General—Editor Theme 然后就可以选是dark还是light了:...
在react中组件间过渡动画如何实现?
一、是什么 在日常开发中,页面切换时的转场动画是比较基础的一个场景 当一个组件在显示与消失过程中存在过渡动画,可以很好的增加用户的体验 在react中实现过渡动画效果会有很多种选择,如react-transition-group,react-motion&…...
解析找不到msvcr100.dll文件的解决方法,4个方法修复msvcr100.dll
msvcr100.dll是Microsoft Visual C 2010运行库的组成部分,一些基于Visual C开发的软件运行时会依赖这个dll文件。出现“找不到msvcr100.dll”的错误提示,往往意味着这个文件在你的计算机系统中丢失或损坏,导致相关程序无法正常运行。以下是找…...

达梦主备部署
达梦主备部署 一.概括1)环境软件下载2)集群规划 二.安装1)安装前2)安装数据库 三.主备机器部署1)初始化数据库(1)主库配置(2)备库配置 2)脱机备份(1)主服务器…...

后期混音效果全套插件Waves 14 Complete mac中文版新增功能
Waves 14 Complete for Mac是一款后期混音效果全套插件,Waves音频插件,内置混响,压缩,降噪和EQ等要素到建模的模拟硬件,环绕声和后期制作工具,包含全套音频效果器,是可以让你使用所有功能。Waves 14 Comple…...

HTML5笔记
前端学习笔记专栏区别于官网中全面的知识讲解,主要记录学习技术栈时对于重点内容的提炼,便于对技术栈知识的快速回顾以及使用 1.canvas元素 内部坐标:坐标均以左上角为(0, 0),单一坐标均作为起始坐标创建对象: <c…...

前端架构师需要解决那些问题
假设你是一个大型后台管理系统的前端架构师,你需要解决那些问题? 1、Ui设计规范 大型系统UI得统一吧?各个业务模块的UI设计得高效吧?那就得有规范,直观的说就是原子设计那套东西。加一堆推荐设计稿。 2、基础组件库…...

使用python快速搭建接口自动化测试脚本实战总结
导读 本文将介绍如何使用python快速进行http/https接口自动化测试脚本搭建,实现自动请求、获取结果、数据对比分析,导出结果到Excel等功能,包括python的requests、pandas、openpyxl等库的基本使用方法。 测试需求介绍 通常,在我…...
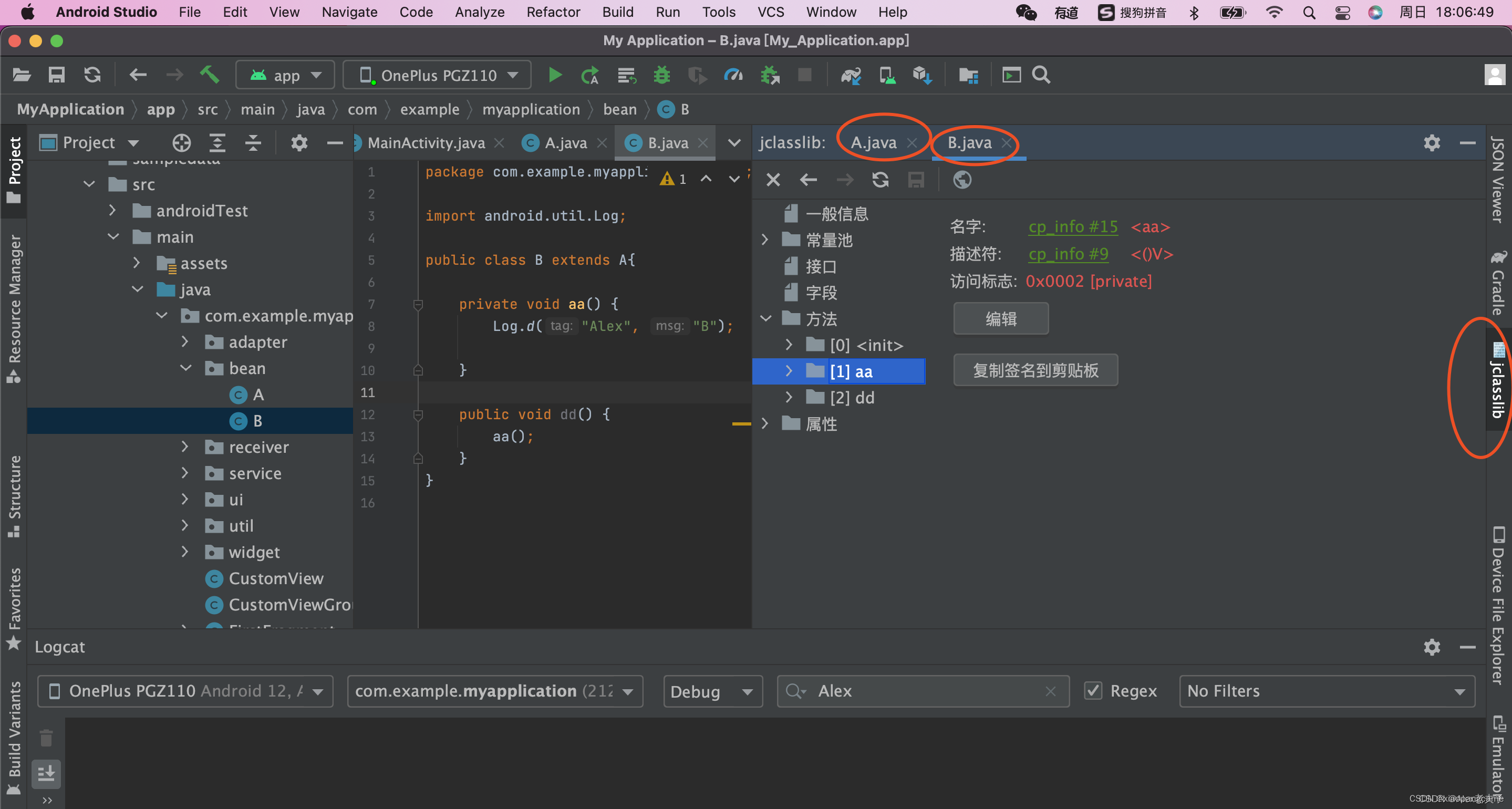
android studio 字节码查看工具jclasslib bytecode viewer
jclasslib bytecode viewer 是一款非常好用的.class文件查看工具; jclasslib bytecode editor is a tool that visualizes all aspects of compiled Java class files and the contained bytecode. Many aspects of class files can be edited in the UI. In addit…...

Ubuntu上搭建FTP服务
要在Ubuntu上搭建FTP服务器,可以使用常见的FTP服务器软件如vsftpd(Very Secure FTP Daemon)或ProFTPD。以下是使用vsftpd在Ubuntu上设置FTP服务器的基本步骤: 步骤 1: 安装 vsftpd 打开终端并运行以下命令安装 vsftpd:…...
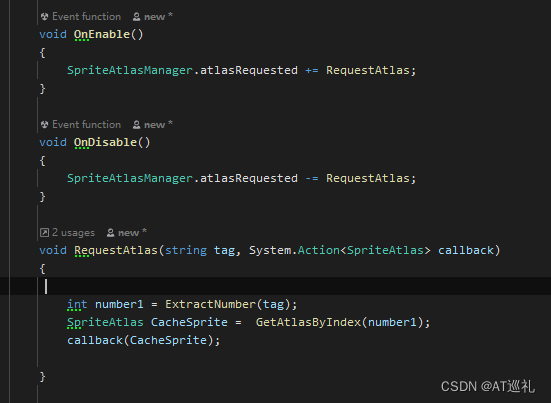
unity打AB包,AssetBundle预制体与图集(三)
警告: spriteatlasmanager.atlasrequested wasn’t listened to while 条件一:图片打图集里面去了 条件二:然后图集打成AB包了 条件三:UI预制体也打到AB包里面去了 步骤一:先加载了图集 步骤二:再加载UI预…...

在Javascript中为什么 0.1+0.2 不等于0.3 ? 源代码详细解析
在JavaScript中,浮点数计算可能会导致精度问题,这就是为什么0.1 0.2不等于0.3的原因。这是因为JavaScript使用IEEE 754标准来表示浮点数,而该标准使用二进制来表示小数。 让我们通过一个实例来详细解释这个问题。考虑以下代码: …...

MATLAB|热力日历图
目录 日历图介绍: 热力日历图的特点: 应用场景: 绘图工具箱 属性 (Properties) 构造函数 (Constructor) 公共方法 (Methods) 私有方法 (Private Methods) 使用方法 日历图介绍: 热力日历图是一种数据可视化形式…...
《golang设计模式》第三部分·行为型模式-05-仲裁者/中介模式(Mediator)
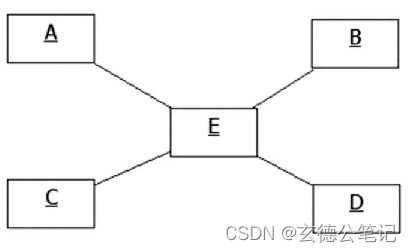
文章目录 1. 概述1.1 作用1.2 角色1.3 类图 2. 代码示例2.1 设计2.2 代码2.3 类图 1. 概述 仲裁者(Mediator)可以封装和协调多个对象之间的耦合交互行为,以减弱这些对象之间的耦合关联。 1.1 作用 将多个对象相互耦合的设计转变为所有对象…...
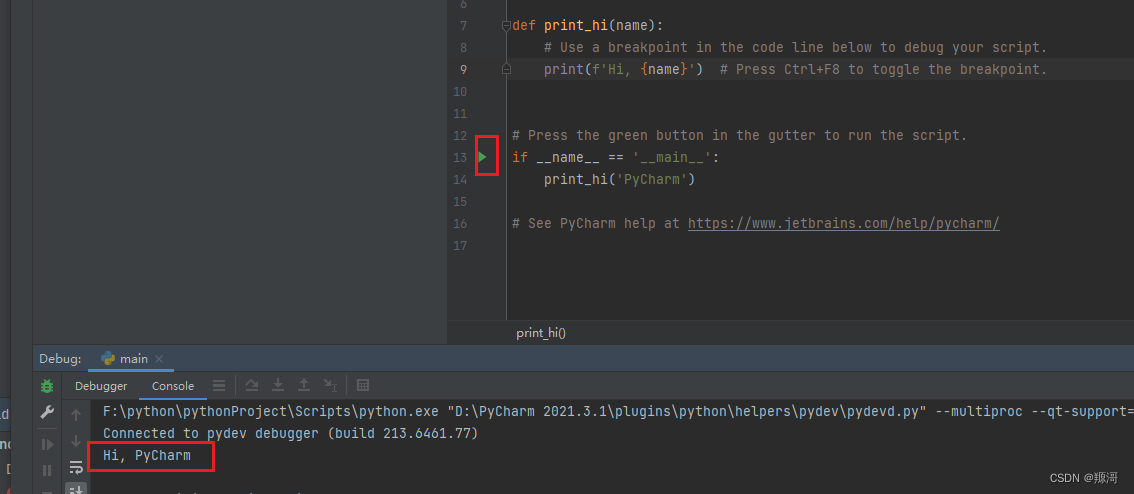
7天入门python系列之准备工作
寄语 编者打算开一个python 初学主题的系列文章,用于指导想要学习python的同学。关于文章有任何疑问都可以私信作者。对于初学者想在7天内入门Python,这是一个紧凑的学习计划。但并不是不可完成的。 7天的安排 如果你想在7天内入门Python,…...

Go语言~反射
reflect包 type name和type kindValueOf通过反射获取值通过反射设置变量的值 package mainimport ("fmt""reflect" )func reflectType(x interface{}) {obj : reflect.TypeOf(x)fmt.Println(obj, obj.Name(), obj.Kind())fmt.Printf("obj type of %…...

详解交叉验证中【KFold】【Stratified-KFold】【StratifiedShuffleSplit】的区别
交叉验证是一种统计分析方法,它的目的是通过在同一数据集上重复并分割训练和测试数据,来评估机器学习模型的性能。以下是这三种交叉验证方法的区别: KFold(K-折叠) 在KFold交叉验证中,原始数据集被分为K个…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...
