NOIP2023模拟14联测35 charlotte
题目大意
给你一棵有 n n n个节点的树,并用 01 01 01串告诉你哪些节点上有棋子(恰好一棵)。
你可以进行若干次操作,每次操作可以将两颗距离至少为 2 2 2的棋子向彼此移动一步。
问能否通过若干次操作使得所有的棋子都在一个点上。如果能,输出最小操作次数;否则,输出 − 1 -1 −1。
1 ≤ n ≤ 1 0 6 1\leq n\leq 10^6 1≤n≤106
时间限制 2000 m s 2000ms 2000ms,空间限制 256 M B 256MB 256MB。
题解
看这道题之前可以先看看AGC034E Complete Compress,本题为其加强版。
我们可以枚举最后所有棋子聚集在哪个点,设这个点为 r r r,我们设 r r r为根。
设 d i s u dis_u disu表示 u u u的子树中每个棋子到 u u u的距离,那每一次操作会使 d i s r dis_r disr减少 2 2 2或者不变。我们发现, 如果不变的话,相当于浪费了一次,所以最优的肯定是选择减少 2 2 2。
每次减少 2 2 2,要不是在 r r r的一个儿子的 d i s dis dis值减少 2 2 2,要不是在 r r r的两个儿子分别减少 1 1 1。我们考虑什么时候无解,无解就是子树不能抵消完。设 m n u mn_u mnu表示子树 u u u中的棋子在内部操作若干次,直到不能再操作时的 d i s u dis_u disu(也就是需要与其他子树操作的最小次数)。设 v v v为 u u u的儿子,我们比较 m n v + s i z v mn_v+siz_v mnv+sizv和 d i s u − d i s v − s i z v dis_u-dis_v-siz_v disu−disv−sizv的大小( s i z v siz_v sizv表示子树 v v v中的棋子个数):
- 如果 m n v + s i z v ≤ d i s u − d i s v − s i z v mn_v+siz_v\leq dis_u-dis_v-siz_v mnv+sizv≤disu−disv−sizv,那就是能抵消完,最后剩的就是 m n u = d i s u % 2 mn_u=dis_u\%2 mnu=disu%2
- 如果 m n v + s i z v > d i s u − d i s v − s i z v mn_v+siz_v>dis_u-dis_v-siz_v mnv+sizv>disu−disv−sizv,就不能抵消完,那我们拿其他部分来抵消 m n v mn_v mnv, m n u = m n v + s i z v − ( d i s u − d i s v − s i z v ) mn_u=mn_v+siz_v-(dis_u-dis_v-siz_v) mnu=mnv+sizv−(disu−disv−sizv)
我们记录 u u u的所有儿子 v v v的 m n v + d i s v + 2 s i z v mn_v+dis_v+2siz_v mnv+disv+2sizv的最大值 m x u mx_u mxu,然后用这个最大值来与 d i s u dis_u disu作比较即可。
最后,看 m n r mn_r mnr是否为 0 0 0。如果为 0 0 0,则可以抵消完,则用 d i s r / 2 dis_r/2 disr/2来更新答案(这里的 d i s r dis_r disr是最开始的 d i s r dis_r disr);否则,以 r r r为最终聚集的点是无解的。
时间复杂度为 O ( n 2 ) O(n^2) O(n2)。下面考虑优化。
我们可以用换根 D P DP DP。设 s u m u sum_u sumu表示所有棋子到 u u u的距离,然后和上面类似地维护 f a d i s u fadis_u fadisu表示以 u u u为根节点,除去 u u u的子树部分之外的所有棋子到 u u u的距离, f a m n u famn_u famnu表示以 u u u为根节点时除去 u u u子树部分之外的部分内部操作若干次,直到不能再操作时的 d i s u dis_u disu。其实和上面的定义是类似的,只不过上面是在 u u u的子树中,这里是在 u u u的子树之外。
因为在更新 u u u的儿子 v v v的 f a m n v famn_v famnv时有可能用到自己的 m n v + d i s v + 2 s i z v mn_v+dis_v+2siz_v mnv+disv+2sizv,所以我们在记录 m n v + d i s v + 2 s i z v mn_v+dis_v+2siz_v mnv+disv+2sizv的最大值时还要记录次大值, m x u , 0 / 1 mx_{u,0/1} mxu,0/1分别表示最大值和次大值。
用与上面类似的方法来维护,然后对每个点判断是否有解,有解就更新答案。
时间复杂度为 O ( n ) O(n) O(n)。
可以参考代码帮助理解。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1000000;
int n,tot=0,d[2*N+5],l[2*N+5],r[N+5],dep[N+5],siz[N+5];
long long ans=1e18,dis[N+5],mn[N+5],fadis[N+5],sum[N+5],famn[N+5],mx[N+5][2];
char s[N+5];
void add(int xx,int yy){l[++tot]=r[xx];d[tot]=yy;r[xx]=tot;
}
void dfs1(int u,int fa){siz[u]=(s[u]=='1');for(int i=r[u];i;i=l[i]){int v=d[i];if(v==fa) continue;dfs1(v,u);siz[u]+=siz[v];dis[u]+=dis[v]+siz[v];long long tmp=dis[v]+siz[v]*2+mn[v];if(tmp>mx[u][0]){mx[u][1]=mx[u][0];mx[u][0]=tmp;}else if(tmp>mx[u][1]) mx[u][1]=tmp;}if(mx[u][0]<=dis[u]) mn[u]=dis[u]%2;else mn[u]=mx[u][0]-dis[u];
}
void dfs2(int u,int fa){for(int i=r[u];i;i=l[i]){int v=d[i];if(d[i]==fa) continue;long long now=dis[u]-dis[v]-siz[v];fadis[v]=now+siz[1]-siz[v]+fadis[u];sum[v]=dis[v]+fadis[v];long long famx=mx[u][0],fasum=sum[u]-dis[v]-siz[v];if(famx==dis[v]+siz[v]*2+mn[v]) famx=mx[u][1];famx=max(famx,famn[u]+fadis[u]);if(famx<=fasum) famn[v]=fasum%2+siz[1]-siz[v];else famn[v]=famx-fasum+siz[1]-siz[v];long long mxd=max(mx[v][0],fadis[v]+famn[v]);if(mxd<=sum[v]&&sum[v]%2==0) ans=min(ans,sum[v]/2);dfs2(v,u);}
}
int main()
{
// freopen("charlotte.in","r",stdin);
// freopen("charlotte.out","w",stdout);scanf("%d",&n);scanf("%s",s+1);for(int i=1,x,y;i<n;i++){scanf("%d%d",&x,&y);add(x,y);add(y,x);}dfs1(1,0);if(mn[1]==0) ans=dis[1]/2;sum[1]=dis[1];dfs2(1,0);if(ans==1e18) printf("-1\n");else printf("%lld\n",ans);return 0;
}
相关文章:

NOIP2023模拟14联测35 charlotte
题目大意 给你一棵有 n n n个节点的树,并用 01 01 01串告诉你哪些节点上有棋子(恰好一棵)。 你可以进行若干次操作,每次操作可以将两颗距离至少为 2 2 2的棋子向彼此移动一步。 问能否通过若干次操作使得所有的棋子都在一个点上…...

绿色科技和可持续发展技术
一、绿色科技和可持续发展技术的定义 绿色科技和可持续发展技术是指那些利用可再生资源、减少环境污染和促进可持续发展的技术。这些技术不仅可以提高人们的生活质量,同时也可以减少对自然环境的破坏,并且能够为未来的可持续发展提供保障。 二、绿色科…...

建链时,please install openssl! use “openssl version“ command to check.
please install openssl! use “openssl version” command to check. 但是我已经安装了 编辑build_chain.sh文件 也可以用vi或者gedit命令 将 [ ! -z “ ( o p e n s s l v e r s i o n ∣ g r e p 1.0.2 ) " ] ∣ ∣ [ ! − z " (openssl version | grep 1.0.2)…...
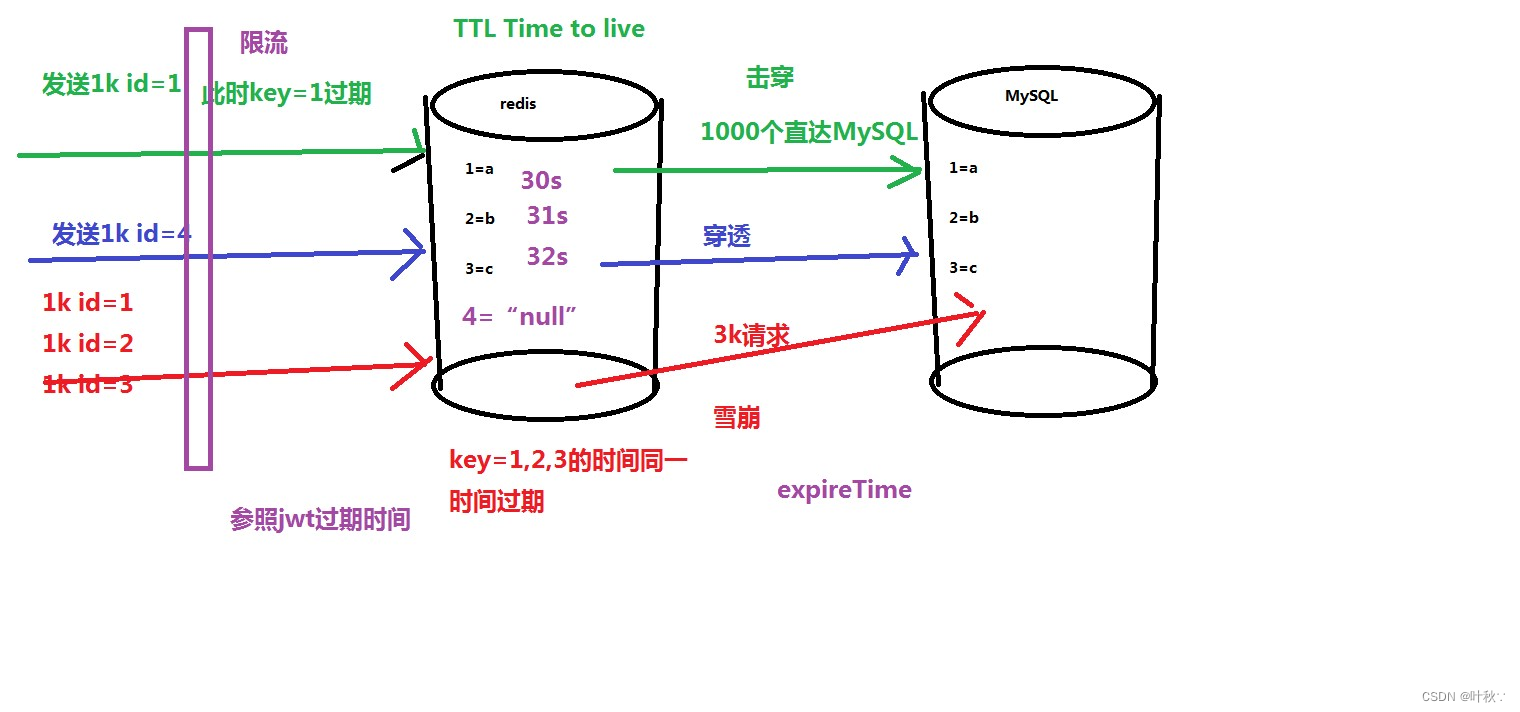
“Redis与Spring整合及缓存优化“
文章目录 引言1. Spring整合Redis1.1. 为什么选择Redis作为缓存解决方案?Redis的特点和优势Redis与传统关系数据库的对比 1.2. Spring与Redis整合的基本步骤 2. Redis注解式缓存2.1. Spring提供的缓存注解介绍2.2. 使用注解实现方法级别的缓存 3. Redis的击穿、穿透…...
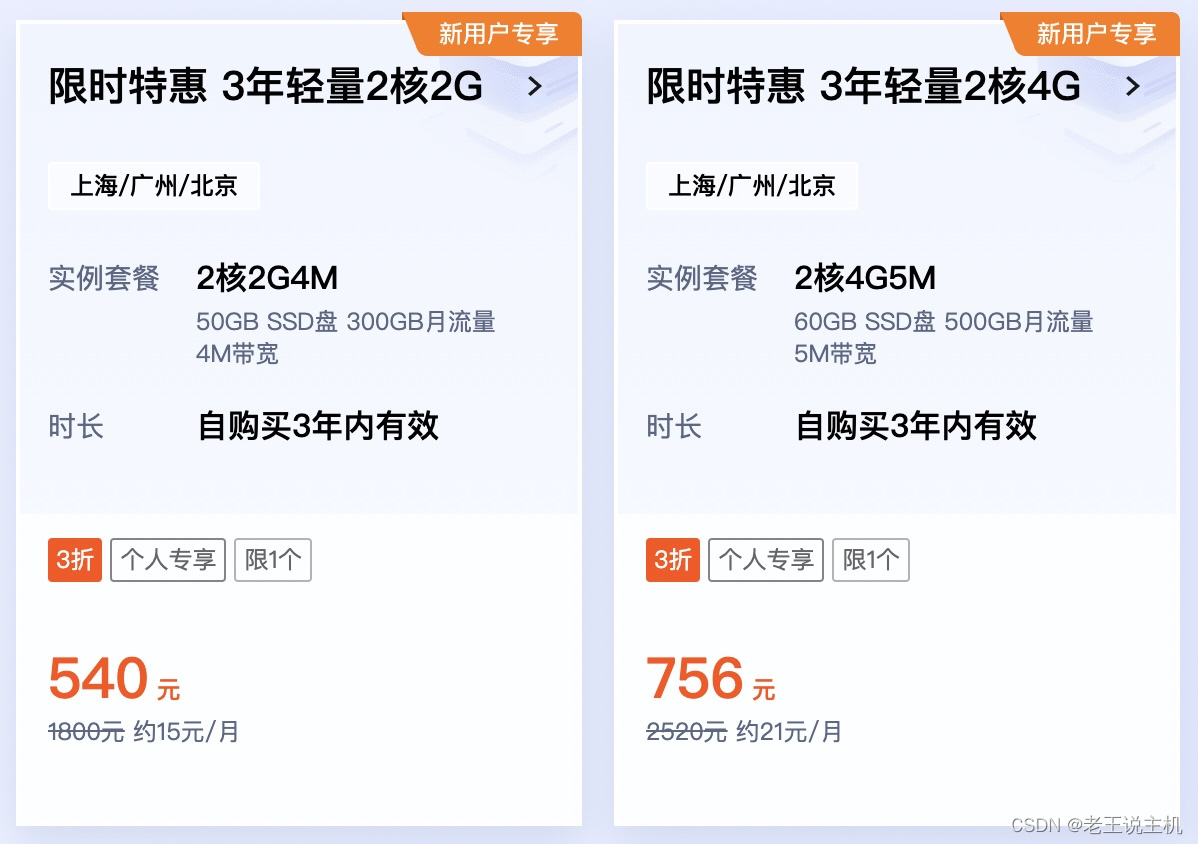
腾讯云3年云服务器价格及购买教程
腾讯云作为国内领先的云计算服务提供商,提供了多种优惠的云服务器套餐,以满足不同用户的需求,本文将详细介绍腾讯云3年云服务器价格及购买教程,新老用户均可购买! 1、活动页面:传送门>>> 2、进入…...

cortex-A7核 中断实验(按键中断实验)
1.选择按键触发方式 下降沿 2.解决消抖的方法 1)ARM中:延时消抖 2)linux驱动开发:定时器函数 3.框图 内部流程框图: 需要RCC GPIO EXTI GIC章节 中断触发流程: 4.RCC 章节 1)使能GPIOF组 …...
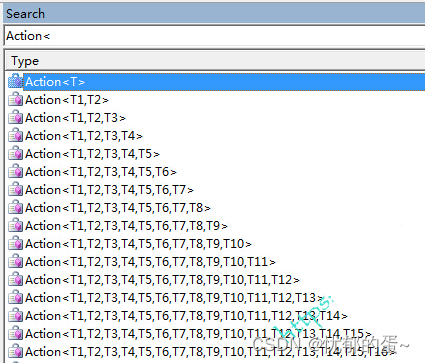
.NET Framework中自带的泛型委托Action
Action<>是.NET Framework中自带的泛型委托,可以接收一个或多个输入参数,但不返回任何参数,可传递至多16种不同类型的参数类型。在Linq的一些方法上使用的比较多。 1、Action泛型委托 .NET Framework为我们提供了多达16个参数的Action…...
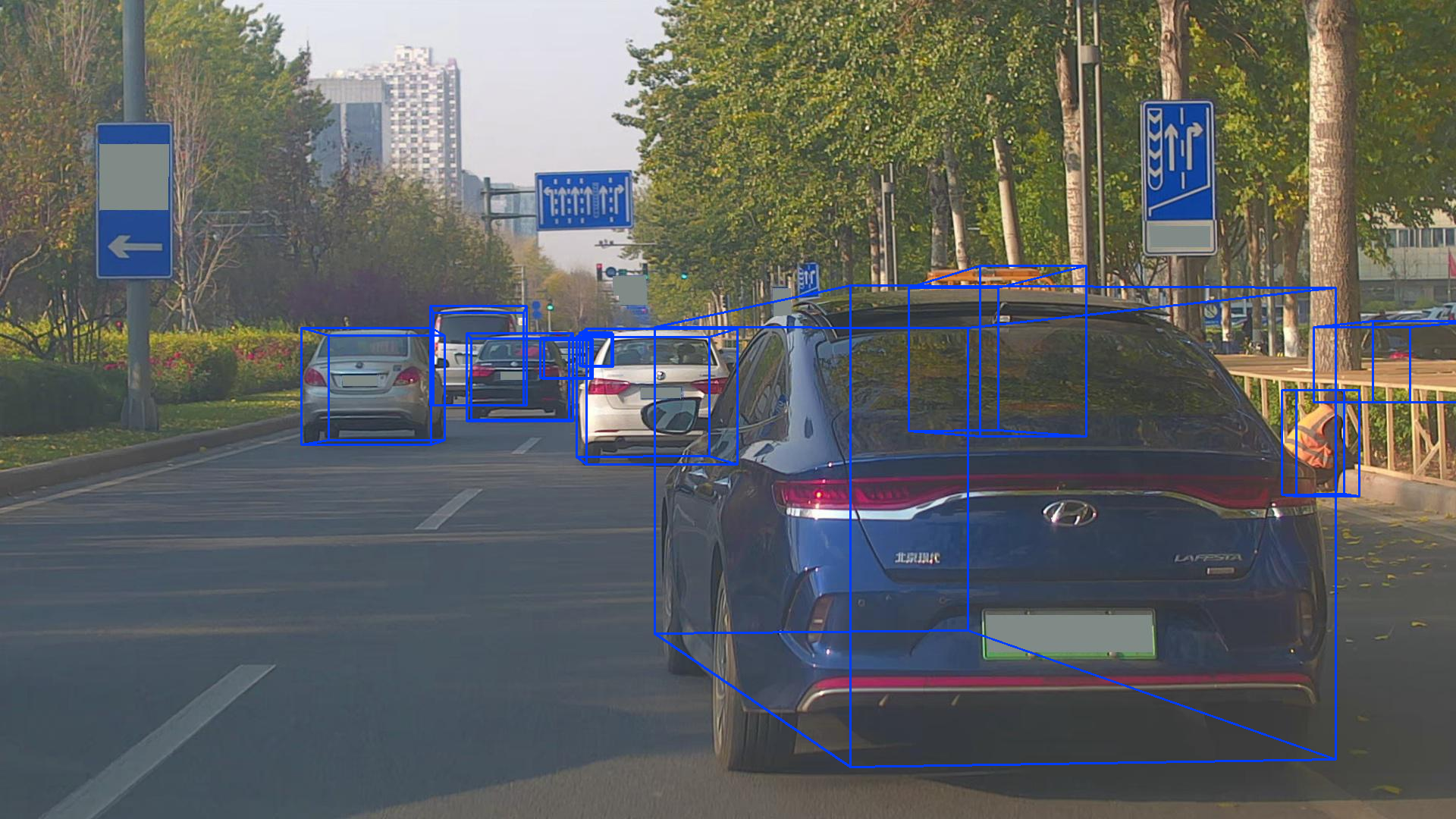
DAIR-V2X-V 3D检测数据集 转为Kitti格式 | 可视化
本文分享在DAIR-V2X-V数据集中,将标签转为Kitti格式,并可视化3D检测效果。 一、将标签转为Kitti格式 DAIR-V2X包括不同类型的数据集: DAIR-V2X-IDAIR-V2X-VDAIR-V2X-CV2X-Seq-SPDV2X-Seq-TFDDAIR-V2X-C-Example: google_drive_linkV2X-Seq-…...
深入理解指针:【探索指针的高级概念和应用二】
目录 一,数组参数、指针参数 1.一维数组传参 2.二维数组传参 3.一级指针传参 4.二级指针传参 二,函数指针 三,函数指针数组 🍂函数指针数组的用途(转移表): 四,指向函数指针…...

腾讯觅影数智医疗影像平台获颁世界互联网领先科技成果大奖
11月8日,2023年世界互联网大会乌镇峰会在乌镇举行,腾讯再度获颁“世界互联网领先科技成果”大奖。腾讯健康总裁吴文达在世界互联网领先科技成果发布活动中介绍,“腾讯觅影数智医疗影像平台”已全面开放20多个医疗AI引擎助力科研创新ÿ…...

鸿蒙开发工具DevEco Studio的下载和安装
一、DevEco Studio概述 1、简介 HUAWEI DevEco Studio(获取工具请单击链接下载,以下简称DevEco Studio)是基于IntelliJ IDEA Community开源版本打造,为运行在HarmonyOS和OpenHarmony系统上的应用和服务(以下简称应用…...
【原理篇】四、自定义starter
文章目录 1、案例分析2、业务功能的实现3、中途调试4、开启定时任务打印报表5、引入属性配置类,写活业务参数配置6、拦截器7、开启yml提示功能 做一个记录系统访客独立IP访问次数的功能,并把它自定义成一个starter,实现:在现有项目…...
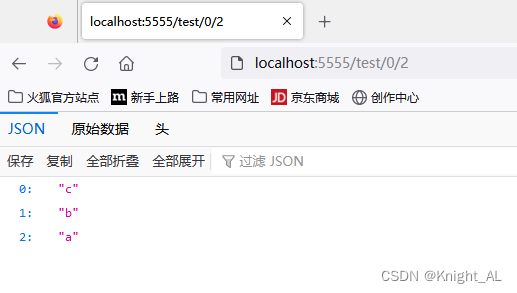
redisTemplate不支持zpopmax,解决方案使用reverseRangeWithScore
在redis客户端可以使用zpopmax redisTemplate不支持zpopmax 解决方案 使用reverseRangeWithScore 接下来我们进行测试 我们要返回最大的value,应该是c import org.junit.Test; import org.junit.runner.RunWith; import org.springframework.beans.factory.a…...
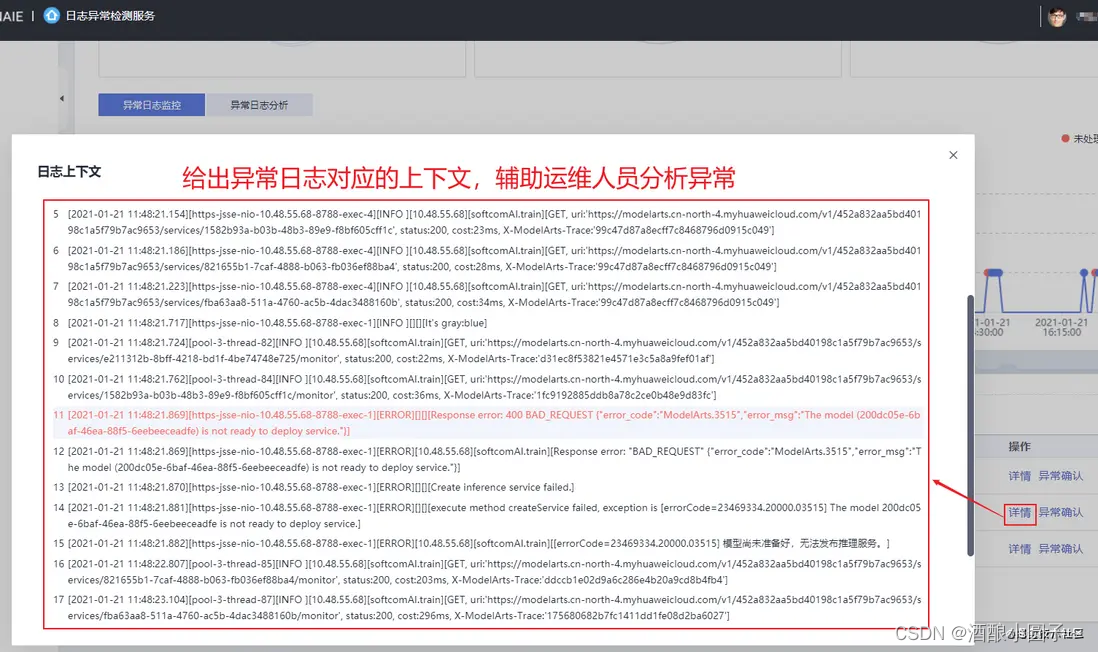
基于深度模型的日志异常检测
本文转载自:深度模型的日志异常检测,还有谁不会?PPT下载地址:https://bbs.huaweicloud.com/forum/thread-100052-1-1.html视频讲解地址:https://bbs.huaweicloud.com/live/DevRun_live/202101222000.html 文章目录 1. …...

最大连续子数组
最大连续子数组(Maximum Subarray)问题是一个经典的算法问题,其目标是在给定的整数数组中找到一个连续的子数组,使得该子数组的元素之和最大。这个问题有多种解决方法,其中包括暴力解法、分治法和动态规划等。 下面是…...
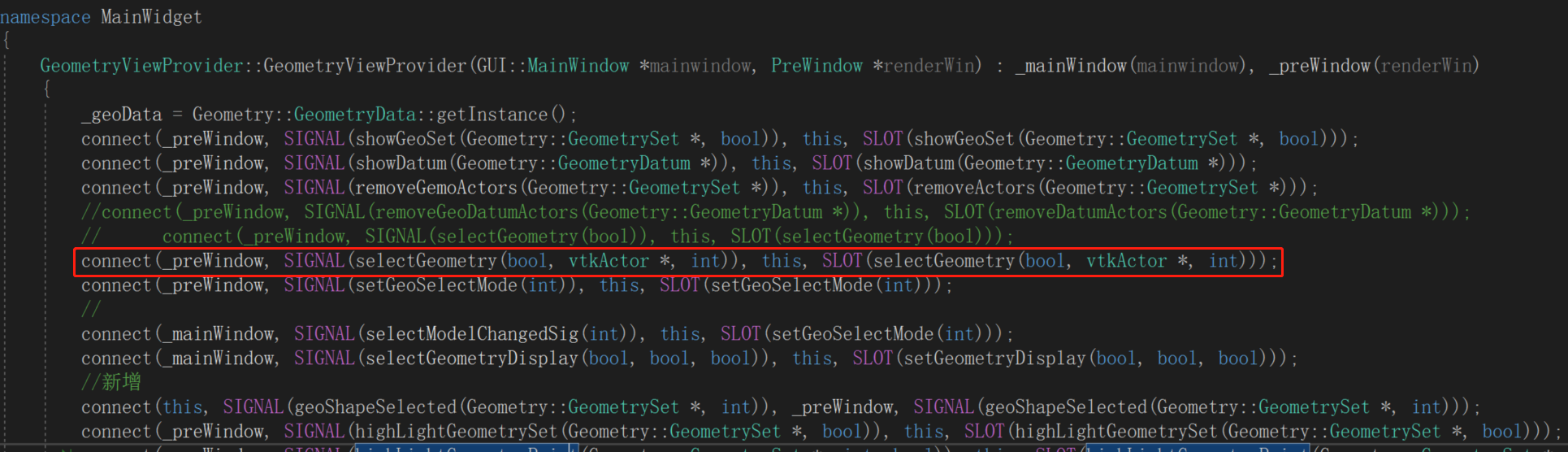
【FastCAE源码阅读5】使用VTK实现鼠标拾取对象并高亮
鼠标拾取对象是很多软件的基本功能。FastCAE的拾取比较简单,是通过VTK实现的。 对几何而言,拾取类型切换在工具栏上,单击后再来单击视图区对象进行拾取,拾取后的对象会高亮显示。效果如下图: 一、拾取对象 拾取对象…...
【全志H616 使用标准库 完成自制串口库(分文件实现) orangepi zero2(开源)】.md updata: 23/11/07
文章目录 H616 把玩注意:Linux内核版本5.16 及以上,需手动配置i2c-3 uart5驱动配置示例 分文件编译时需将每个文件一同编译 (空格隔开)例: ggc a.c b.c b.h -lpthread -lxxx..; 常用命令查看驱动文件查看内核检测信息/…...
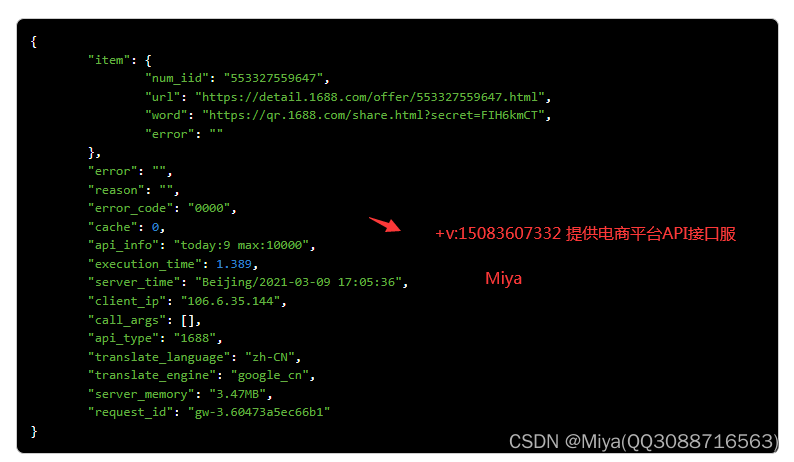
小白学爬虫:手机app分享商品短连接获取淘宝商品链接接口|淘宝淘口令接口|淘宝真实商品链接接口|淘宝商品详情接口
通过手机APP分享的商品短链接,我们可以调用相应的接口来获取淘口令真实URL,进而获取到PC端的商品链接及商品ID。具体步骤如下: 1、通过手机APP分享至PC端的短链接,调用“item_password”接口。 2、该接口将返回淘口令真实URL。 3…...

python 应用之 request 请求调用
场景: 验证一个第三方接口 目录 一、应用实例 1、预准备工作 1)、引用包 2)、生成随机串 3)、获得当前时间戳 4)、HASH 5)、header处理 6)、请求处理 2、requests请求 1)…...
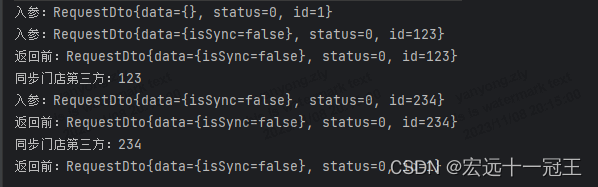
BeanUtils.copyProperties浅拷贝的坑你得知道?
今天想写一篇文章,主要关于深拷贝和浅拷贝相关的,主要是最近写代码的时候遇到一个BUG,刚好涉及到浅拷贝导致的问题。 问题背景 现在有一个需要是需要修改门店信息,门店也区分父门店和子门店,父门店被编辑更新是需要通过…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
