最大连续子数组

最大连续子数组(Maximum Subarray)问题是一个经典的算法问题,其目标是在给定的整数数组中找到一个连续的子数组,使得该子数组的元素之和最大。这个问题有多种解决方法,其中包括暴力解法、分治法和动态规划等。
下面是一个讲解最大连续子数组问题的常见解决方法:
-
暴力解法: 暴力解法是最简单的方法,它通过两层嵌套循环遍历所有可能的子数组,计算它们的和,并找到和最大的子数组。这个方法的时间复杂度是O(n^2),其中n是数组的长度。尽管它不是最高效的方法,但它是一个朴素而容易理解的解决方案。
-
动态规划: 动态规划是解决最大连续子数组问题的高效方法之一。在这种方法中,我们维护一个动态规划数组
dp,其中dp[i]表示以第i个元素结尾的最大子数组和。动态规划的关键是通过递推关系来计算dp[i],这个关系通常是dp[i] = max(dp[i-1] + nums[i], nums[i])。最终,最大子数组和就是dp数组中的最大值。这个方法的时间复杂度是O(n),其中n是数组的长度。 -
分治法: 分治法是另一种解决最大连续子数组问题的方法。它将数组分成三个部分:左子数组、右子数组和跨越中间的子数组。然后,递归地求解左子数组和右子数组的最大子数组和,以及跨越中间的最大子数组和。最后,将这三者中的最大值作为最终的结果。这个方法的时间复杂度是O(n*log(n)),其中n是数组的长度。
-
Kadane算法: Kadane算法是一种高效的动态规划方法,用于解决最大连续子数组问题。它维护两个变量,
cur表示当前子数组的和,maxv表示最大子数组和。在遍历数组的过程中,它不断更新cur和maxv,并且当cur小于0时,将cur重置为0。最终,maxv就是最大子数组和。这个方法的时间复杂度是O(n),其中n是数组的长度。
我们来看看代码
int fun04(int* p, int left, int right);
void fun()
{int i=0, j=0, k=0;int len;int maxv;int v[] = { 1,-3,6,8,0,-7,8 };len = 7; maxv = v[0];for (int i = 0; i < len; i++){for (j = i; j < len; j++){if (j == i){maxv = max(maxv, v[j]);}else {v[i] += v[j];maxv = max(maxv, v[i]);}}}cout << maxv << endl;
}
void fun01()
{int v[] = { 1,-3,6,8,0,-7,8 };int dp[7];dp[0] = v[0];int maxv = dp[0];for (int i = 1; i < 7; i++){dp[i] = max(dp[i - 1] + v[i], v[i]);maxv = max(maxv, dp[i]);}cout << maxv << endl;
}void fun02() {int v[] = { -2,-1 };int maxv = v[0];int cur = 0; for (int i = 0; i < 2; i++) {cur += v[i];maxv = max(maxv, cur);if (cur >= 0) {maxv = max(maxv, cur);}else {cur = 0;}}cout << maxv << endl;
}void fun03() {int v[] = { 1,-3,6,8,0,-7,8 };cout << fun04(v, 0, 6);
}
int fun04(int* p, int left, int right) {if (left == right) {return p[left];}int mid = (left + right) >> 1;int maxleft = fun04(p, left, mid);int maxright = fun04(p, mid + 1, right);int tmpleft = p[mid - 1];int tmp = tmpleft;for (int i = mid - 2; i >= 0; i--) {tmp += p[i];tmpleft = max(tmp, tmpleft);}int tmpright = p[mid + 1];tmp = tmpright;for (int i = mid + 2; i < right; i++){tmp += p[i];tmpright = max(tmp, tmpright);}int midmax = p[mid] + (tmpleft > 0 ? tmpleft : 0) + (tmpright > 0 ? tmpright : 0);return max(maxleft, maxright > midmax ? maxright : midmax);
}上面的代码演示了几种不同的方法来找到数组中的最大子数组和(最大子序列和问题),并进行了简要的分析。
-
fun()方法使用了嵌套的两个 for 循环来遍历所有可能的子数组和,同时维护最大值。这是一种朴素的暴力解法,时间复杂度为O(n^2),其中n是数组的长度。 -
fun01()方法使用了动态规划的思想,维护一个dp数组,其中dp[i]表示以第i个元素结尾的最大子数组和。在遍历数组的过程中,根据前一个元素的最大子数组和来计算当前元素的最大子数组和,从而避免了重复计算。这种方法的时间复杂度为O(n),其中n是数组的长度。 -
fun02()方法是一种更简单的方法,它遍历一次数组,同时维护当前子数组的和cur和最大子数组和maxv。当cur小于0时,表示当前子数组和不再对最大子数组和有贡献,需要将cur重置为0。这种方法也是O(n)时间复杂度。 -
fun03()方法是一个递归的分治方法,其中fun04()函数采用分治思想来寻找最大子数组和。它将数组分为左右两部分,然后分别计算左部分、右部分以及跨越中间的最大子数组和,然后取三者中的最大值作为最终的结果。这个方法的时间复杂度也是O(n*log(n)),因为它每次将数组分成两半,需要进行递归处理。
总的来说,动态规划方法(fun01()和fun02())是解决最大子数组和问题的较优解,具有O(n)的时间复杂度,而分治方法(fun03())也是一个有效的算法,但在实际情况中可能不如动态规划方法高效。朴素的暴力解法(fun())具有O(n^2)的时间复杂度,不适用于大规模数据。选择合适的算法取决于实际问题和性能要求。
相关文章:

最大连续子数组
最大连续子数组(Maximum Subarray)问题是一个经典的算法问题,其目标是在给定的整数数组中找到一个连续的子数组,使得该子数组的元素之和最大。这个问题有多种解决方法,其中包括暴力解法、分治法和动态规划等。 下面是…...
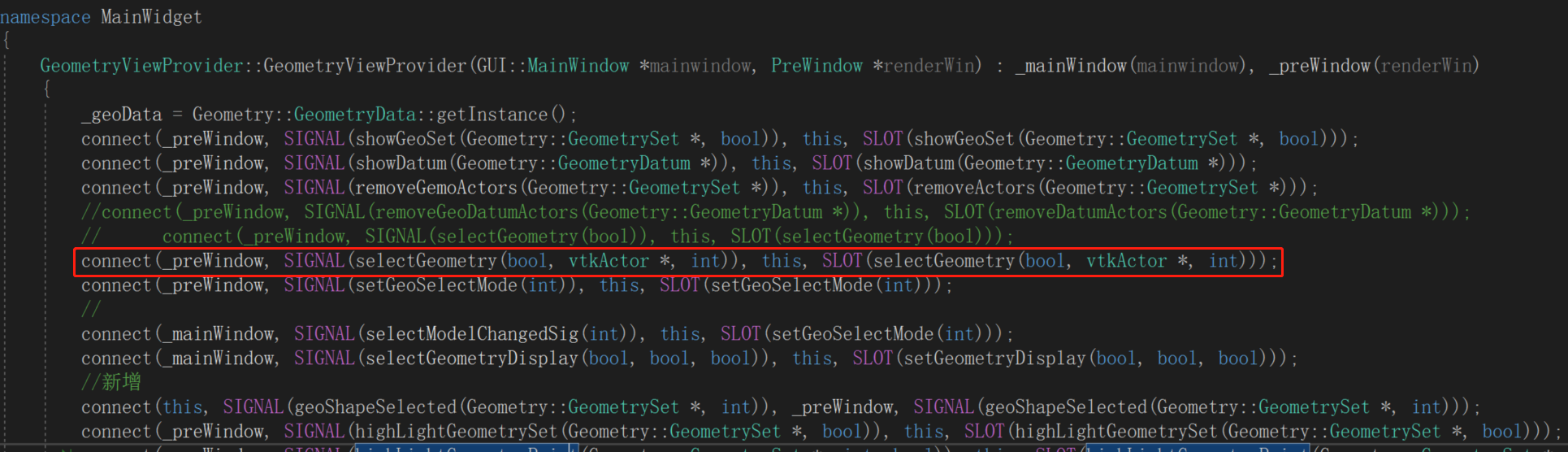
【FastCAE源码阅读5】使用VTK实现鼠标拾取对象并高亮
鼠标拾取对象是很多软件的基本功能。FastCAE的拾取比较简单,是通过VTK实现的。 对几何而言,拾取类型切换在工具栏上,单击后再来单击视图区对象进行拾取,拾取后的对象会高亮显示。效果如下图: 一、拾取对象 拾取对象…...
【全志H616 使用标准库 完成自制串口库(分文件实现) orangepi zero2(开源)】.md updata: 23/11/07
文章目录 H616 把玩注意:Linux内核版本5.16 及以上,需手动配置i2c-3 uart5驱动配置示例 分文件编译时需将每个文件一同编译 (空格隔开)例: ggc a.c b.c b.h -lpthread -lxxx..; 常用命令查看驱动文件查看内核检测信息/…...
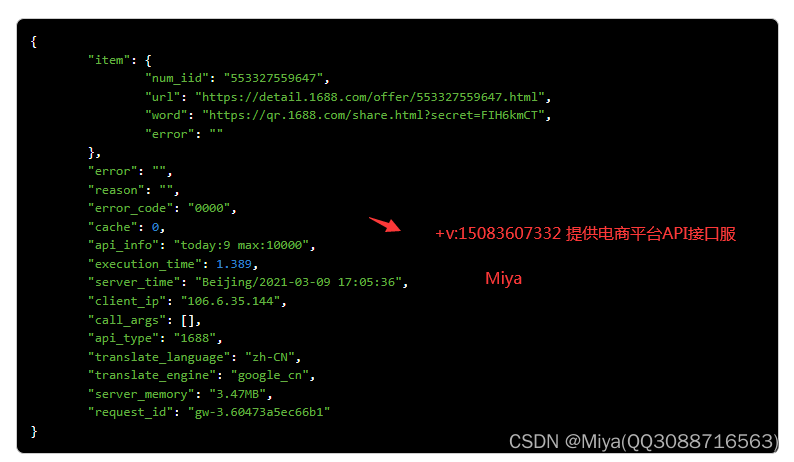
小白学爬虫:手机app分享商品短连接获取淘宝商品链接接口|淘宝淘口令接口|淘宝真实商品链接接口|淘宝商品详情接口
通过手机APP分享的商品短链接,我们可以调用相应的接口来获取淘口令真实URL,进而获取到PC端的商品链接及商品ID。具体步骤如下: 1、通过手机APP分享至PC端的短链接,调用“item_password”接口。 2、该接口将返回淘口令真实URL。 3…...

python 应用之 request 请求调用
场景: 验证一个第三方接口 目录 一、应用实例 1、预准备工作 1)、引用包 2)、生成随机串 3)、获得当前时间戳 4)、HASH 5)、header处理 6)、请求处理 2、requests请求 1)…...
BeanUtils.copyProperties浅拷贝的坑你得知道?
今天想写一篇文章,主要关于深拷贝和浅拷贝相关的,主要是最近写代码的时候遇到一个BUG,刚好涉及到浅拷贝导致的问题。 问题背景 现在有一个需要是需要修改门店信息,门店也区分父门店和子门店,父门店被编辑更新是需要通过…...

ubuntu安装rabbitMQ 并 开启记录消息的日志
apt-get update apt-get install rabbitmq-server rabbitmqctl add_user root password // 设置用户名密码 rabbitmqctl set_user_tags root administrator // 设置为管理员身份 rabbitmqctl set_permissions -p / root ".*" ".*" ".*" //为…...
思维模型 首因效应
本系列文章 主要是 分享 思维模型,涉及各个领域,重在提升认知。先入为主,一见钟情。 1 首因效应的应用 1.1 面试中的首因效应 小李是一名应届毕业生,他准备参加一家知名互联网公司的面试。在面试前,他做了充分的准备…...

Redis极速上手开发手册【Redis全面复习】
文章目录 什么是RedisRedis的特点Redis的应用场景Redis安装部署Redis基础命令Redis多数据库特性Redis数据类型Redis数据类型之stringRedis数据类型之hashRedis数据类型之listRedis数据类型之setRedis数据类型之sorted set案例:存储高一班的学员信息 Redis封装工具类…...
[动态规划] (十四) 简单多状态 LeetCode LCR 091.粉刷房子
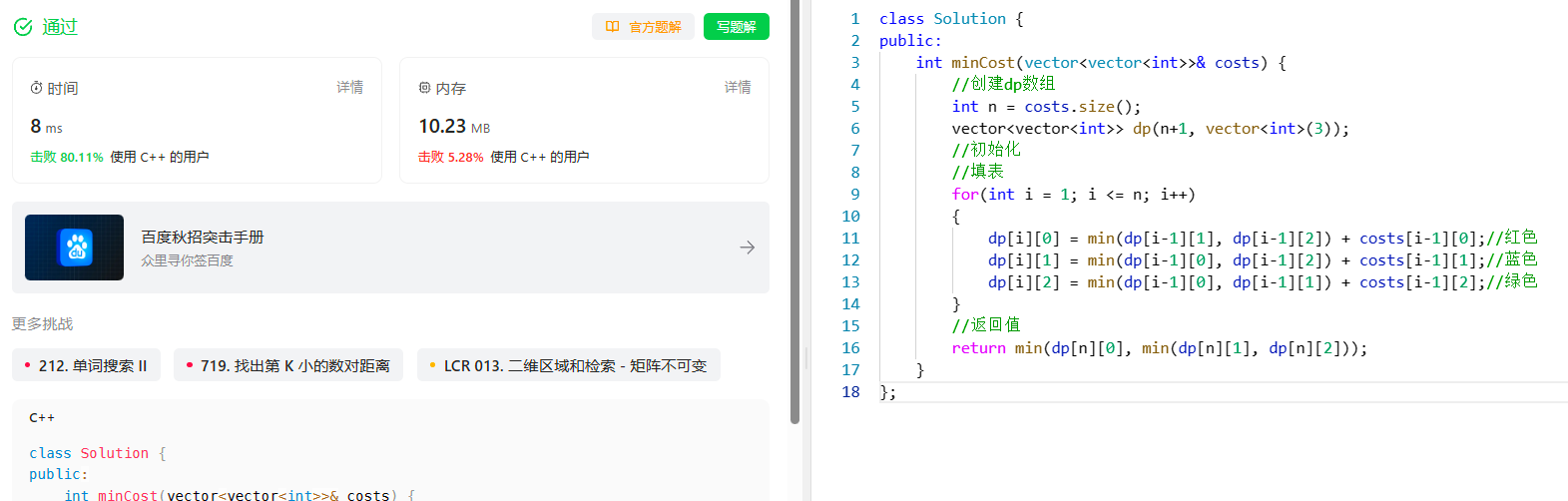
[动态规划] (十四) 简单多状态 LeetCode LCR 091.粉刷房子 文章目录 [动态规划] (十四) 简单多状态 LeetCode LCR 091.粉刷房子题目解析解题思路状态表示状态转移方程初始化和填表顺序返回值 代码实现总结 LCR 091. 粉刷房子 题目解析 (1) 一排房子,共有n个 (2) 染…...

【VSS版本控制工具】
VSS版本控制工具 1 安装 VSS2 服务器端配置3 新建用户4 客户端配置Vss2005Vs20055 客户端详细操作 1 安装 VSS 第一步:将VisualSourceSafe2005安装包解压。 第二步:找到setup.exe双击运行。 第三步:在弹出的界面复选框中选中Iaccepttheterms…...

数据持久化技术(Python)的使用
传统数据库连接方式:mysql(PyMySQL)ORM 模型:SQLAlchemy MyBatis、 Hibernate PyMySQL 安装: pip install pymysql简单使用 利用 pymysql.connect 建立数据库连接并执行 SQL 命令(需要提前搭建好数据库…...
第23章(上)_索引原理之索引与约束
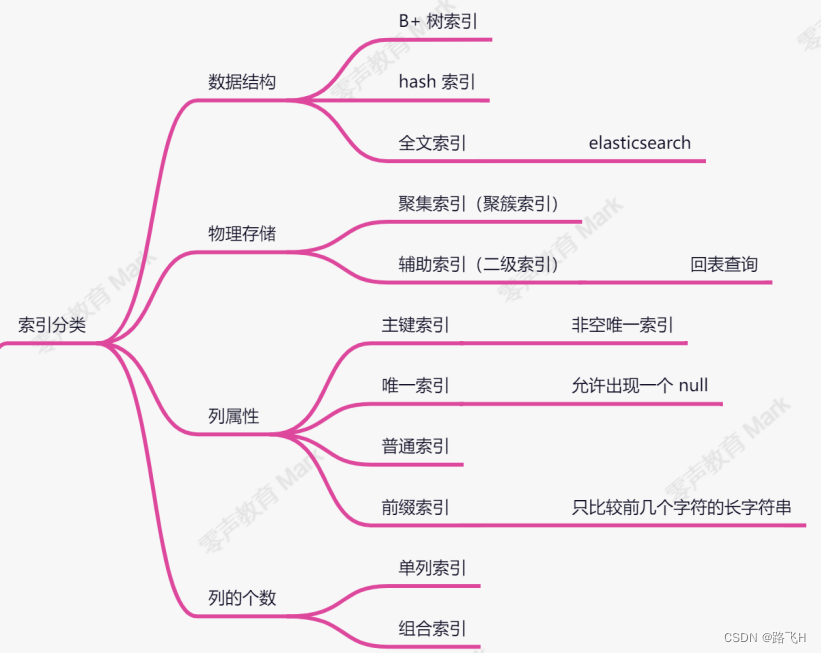
文章目录 索引索引分类主键选择索引的代价 约束外键约束约束与索引的区别 索引使用场景不要使用索引的场景总结 索引 索引的概念:索引是一种有序的存储结构。索引按照单个或多个列的值进行排序。 索引的目的:提升搜索效率。 索引分类 按照数据结构分为…...
金蝶云星空BOS设计器中基础资料字段属性“过滤”设置获取当前界面的基础资料值作为查询条件
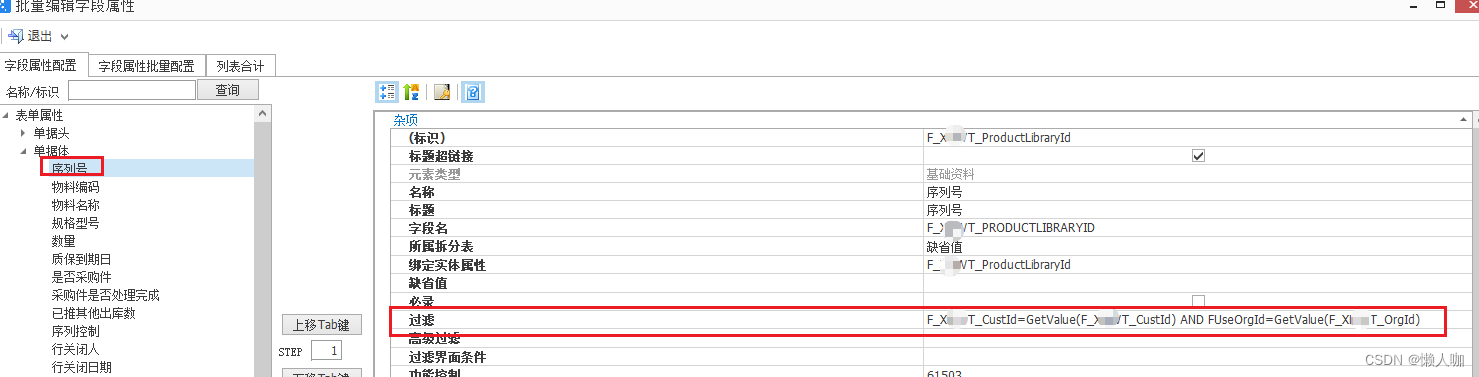
文章目录 金蝶云星空BOS设计器中基础资料字段属性“过滤”设置获取当前界面的基础资料值作为查询条件背景说明业务需求格式BOS配置 金蝶云星空BOS设计器中基础资料字段属性“过滤”设置获取当前界面的基础资料值作为查询条件 背景说明 序列号档案是基础资料,资料里…...
OFDM深入学习及MATLAB仿真
文章目录 前言一、OFDM 基本原理及概念1、OFDM 简介2、子载波3、符号4、子载波间隔与符号长度之间的关系 二、涉及的技术1、保护间隔2、交织3、信道编码4、扩频5、导频6、RF(射频)调制7、信道估计 三、变量间的关系四、IEEE 802.11a WLAN PHY 层标准五、…...

软件测试简历原来是写了这些才让面试官已读不回
前言: 马上就到了面试跳槽涨薪好时候了,最近看很多的小伙伴已经开始投简历了,一天投了几十次几百次,面试官已读不会,面试的机会都没有更别说后面的事情的,这是为什么呢? 很大一部分的原因是的…...

ESP32网络开发实例-Web服务器RGB LED调光
Web服务器RGB LED调光 文章目录 Web服务器RGB LED调光1、RGB LED介绍3、软件准备4、硬件准备4、代码实现在本文中,我们将创建一个 RGB LED 控制器网络服务器。 Web 服务器将显示用于设置 RGB LED 颜色的色谱。 颜色将主要分为三种:红色、绿色和蓝色。 用户将从光谱中选择一种…...

C# TCP Server服务端多线程监听RFID读卡器客户端上传的读卡数据
本示例使用设备介绍:液显WIFI无线网络HTTP协议RFID云读卡器可编程实时可控开关TTS语-淘宝网 (taobao.com) using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using Sy…...

【electron】【附排查清单】记录一次逆向过程中,fetch无法请求http的疑难杂症(net::ERR_BLOCKED_BY_CLIENT)
▒ 目录 ▒ 🛫 导读需求开发环境 1️⃣ Adblock等插件拦截2️⃣ 【失败】Content-Security-Policy启动服务器json-serverhtml中的meta字段 3️⃣ 【失败】https vs httpwebPreferences & allowRunningInsecureContent disable-features 4️⃣ 【失败】检测fetch…...

【JS】scrollTop+scrollHeight+clientTop+clientHeight+offsetTop+offsetHeight
scrollTop、scrollHeight、clientTop、clientHeight、offsetTop以及offsetHeight 1. scrollTop 与 scrollHeight 1.1 scrollTop scrollTop 是这六个属性中唯一一个可写的属性。 Element.scrollTop 属性可以获取或设置一个元素的内容垂直滚动的像素数。 一个元素的 scrollT…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
