排序算法的空间复杂度和时间复杂度
一、排序算法的时间复杂度和空间复杂度
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 最好时间复杂度 | 空间复杂度 | 稳定性 |
| 冒泡排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 |
| 直接选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 不稳定 |
| 直接插入排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 |
| 快速排序 | O(nlogn) | O(n²) | O(nlogn) | O(nlogn) | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 希尔排序 | O(nlogn) | O(n²) | O(nlogn) | O(1) | 不稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(n+k) | 稳定 |
| 基数排序 | O(N*M) | O(N*M) | O(N*M) | O(M) | 稳定 |
注:
1 归并排序可以通过手摇算法将空间复杂度降到O(1),但是时间复杂度会提高。
2 基数排序时间复杂度为O(N*M),其中N为数据个数,M为数据位数。
1.1 复杂度辅助记忆
- 冒泡、选择、直接 排序需要两个for循环,每次只关注一个元素,平均时间复杂度为O(n²))(一遍找元素O(n),一遍找位置O(n))
- 快速、归并、希尔、堆基于二分思想,log以2为底,平均时间复杂度为O(nlogn)(一遍找元素O(n),一遍找位置O(logn))
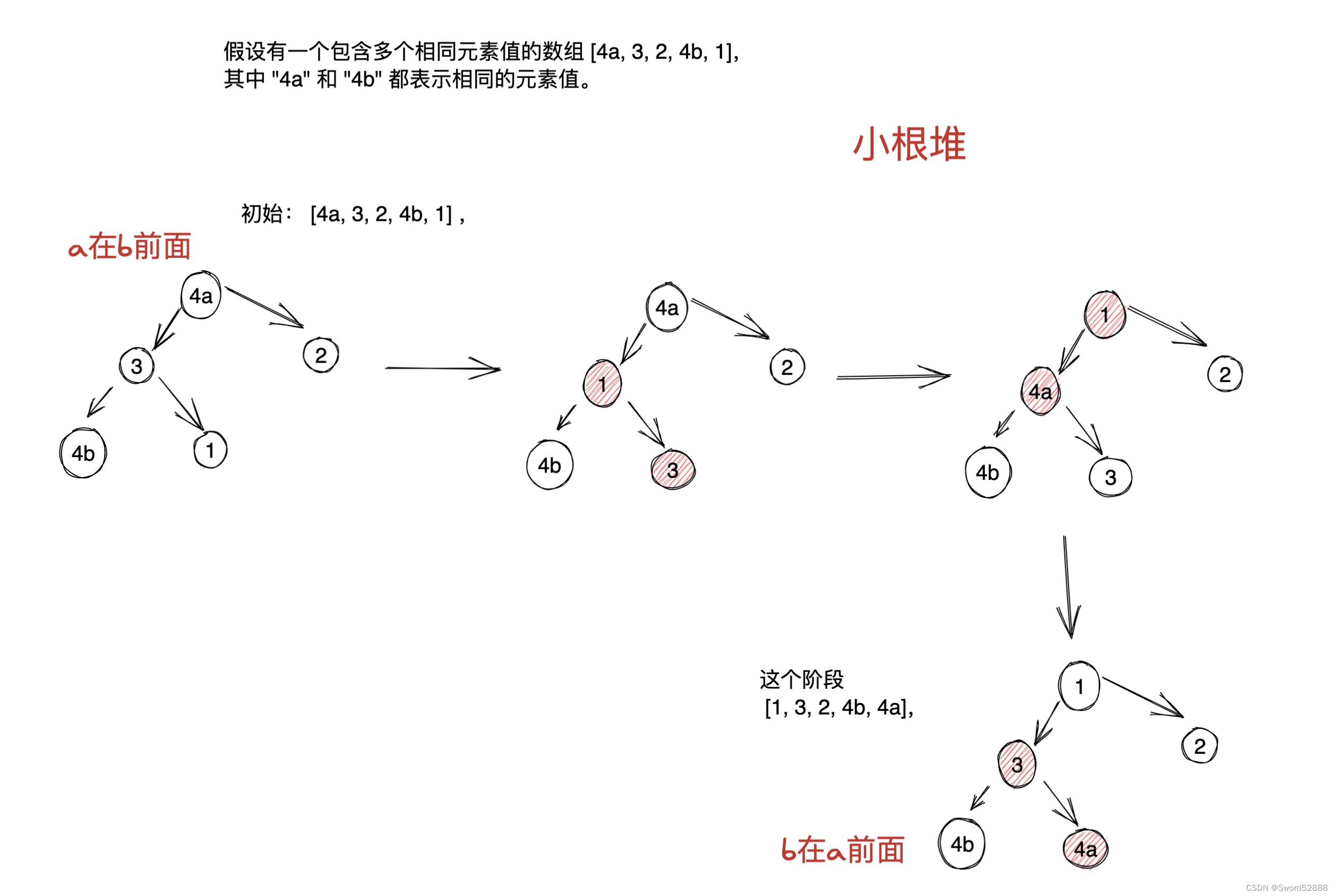
1.2 稳定性辅助记忆
- 稳定性记忆-“快希选堆”(快牺牲稳定性)
- 排序算法的稳定性:排序前后相同元素的相对位置不变,则称排序算法是稳定的;否则排序算法是不稳定的。
二、理解时间复杂度
2.1 常数阶O(1)
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;2.2 对数阶O(logN)
int i = 1;
while(i<n)
{i = i * 2;
}
2.3 线性阶O(n)
for(i=0; i<=n; i++)
{System.out.println("hello");
}2.4 线性对数阶O(n)
for(m=1; m<n; m++)
{i = 1;while(i<n){i = i * 2;}
}2.5 平方阶O(n)
for(x=1; i<=n; x++)
{for(i=1; i<=n; i++){System.out.println("hello");}
}
2.6 K次方阶O(n)
for(i=0; i<=n; i++){for(j=0; i<=n; i++){for(k=0; i<=n; i++){System.out.println("hello");}}}// k = 3 , n ^ 3上面从上至下依次的时间复杂度越来越大,执行的效率越来越低。
三、空间复杂度
3.1 常数阶O(1) —— 原地排序
只用到 temp 这么一个辅助空间
原地排序算法,就是空间复杂度为O(1)的算法,不牵涉额外得到其他空间~
private static void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}2.2 对数阶O(logN)
2.3 线性阶O(n)
int[] newArray = new int[nums.length];for (int i = 0; i < nums.length; i++) {newArray[i] = nums[i];}四、排序算法
4.1 冒泡排序
(思路:大的往后放)

4.1.1 代码
private static void bubbleSort(int[] nums) {for (int i = 0; i < nums.length; i++) {for (int j = 0; j < nums.length - 1 - i; j++) {if (nums[j] > nums[j + 1]) {swap(nums, j, j + 1);}}}}4.1.2 复杂度
时间复杂度: N^2
空间复杂度:1
最佳时间复杂度:N^2 (因为就算你内部循环只对比,不交换元素,也是一样是N)
稳定性:稳定的 (大于的才换,小于等于的不交换)
// { 0,1,2,3,4}private static void bubbleSort(int[] nums) {for (int i = 0; i < nums.length; i++) {boolean isChange = false;for (int j = 0; j < nums.length - 1 - i; j++) {if (nums[j] > nums[j + 1]) {swap(nums, j, j + 1);isChange = true;}}if(!isChange){return;}}}改进后的代码,最佳时间复杂度: N (因为假如第一轮对比就没有任何元素交换,那么可以直接退出,也就是只有一次外循环)
4.2 选择排序
(思路:最小的放最前)
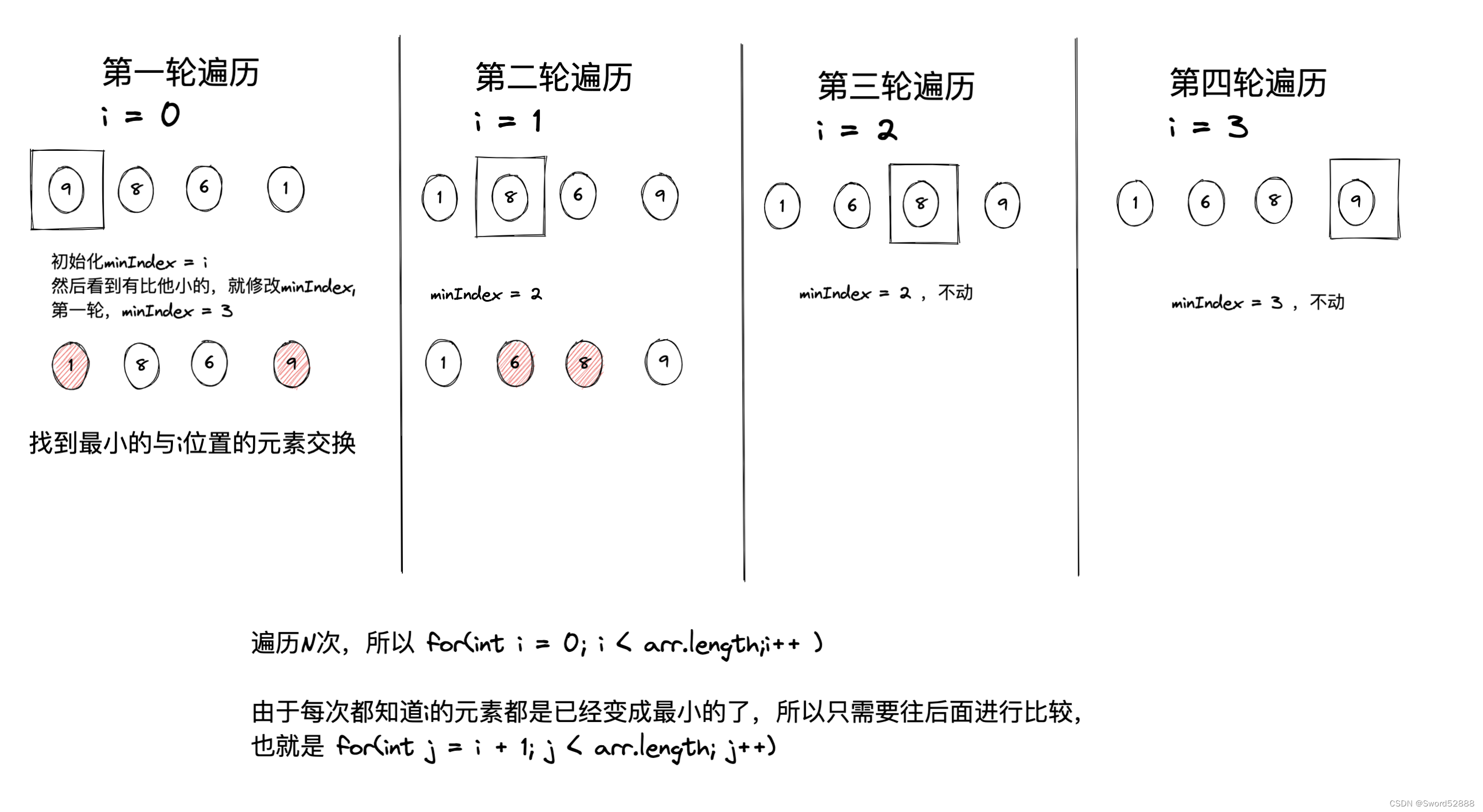
4.2.1 代码
private static void selectSort(int[] nums) {for (int i = 0; i < nums.length; i++) {int minIndex = i;for (int j = i + 1; j < nums.length; j++) {if (nums[j] < nums[minIndex]) {minIndex = j;}}swap(nums,minIndex,i);}}4.2.2 复杂度
时间复杂度: N^2
空间复杂度:1
最佳时间复杂度:N^2
稳定性:不稳定的

4.3 直接插入排序
(思路:往排序好的数组中,找到合适的位置插进去)

4.3.1 代码
private static void insertSort(int[] nums) {for (int i = 1; i < nums.length; i++) {int temp = nums[i];int j = i - 1;for (; j >= 0 && temp < nums[j]; j--) {nums[j + 1] = nums[j];}nums[j + 1] = temp;}}4.3.2 复杂度
时间复杂度: N^2
空间复杂度:1
最佳时间复杂度:N (因为你不进入内部循环。 [1,2,3,4,5])

稳定性:稳定的
4.4 快速排序
(思路:利用数字target,把数组切成两边,左边比 target大,后边比 target小)
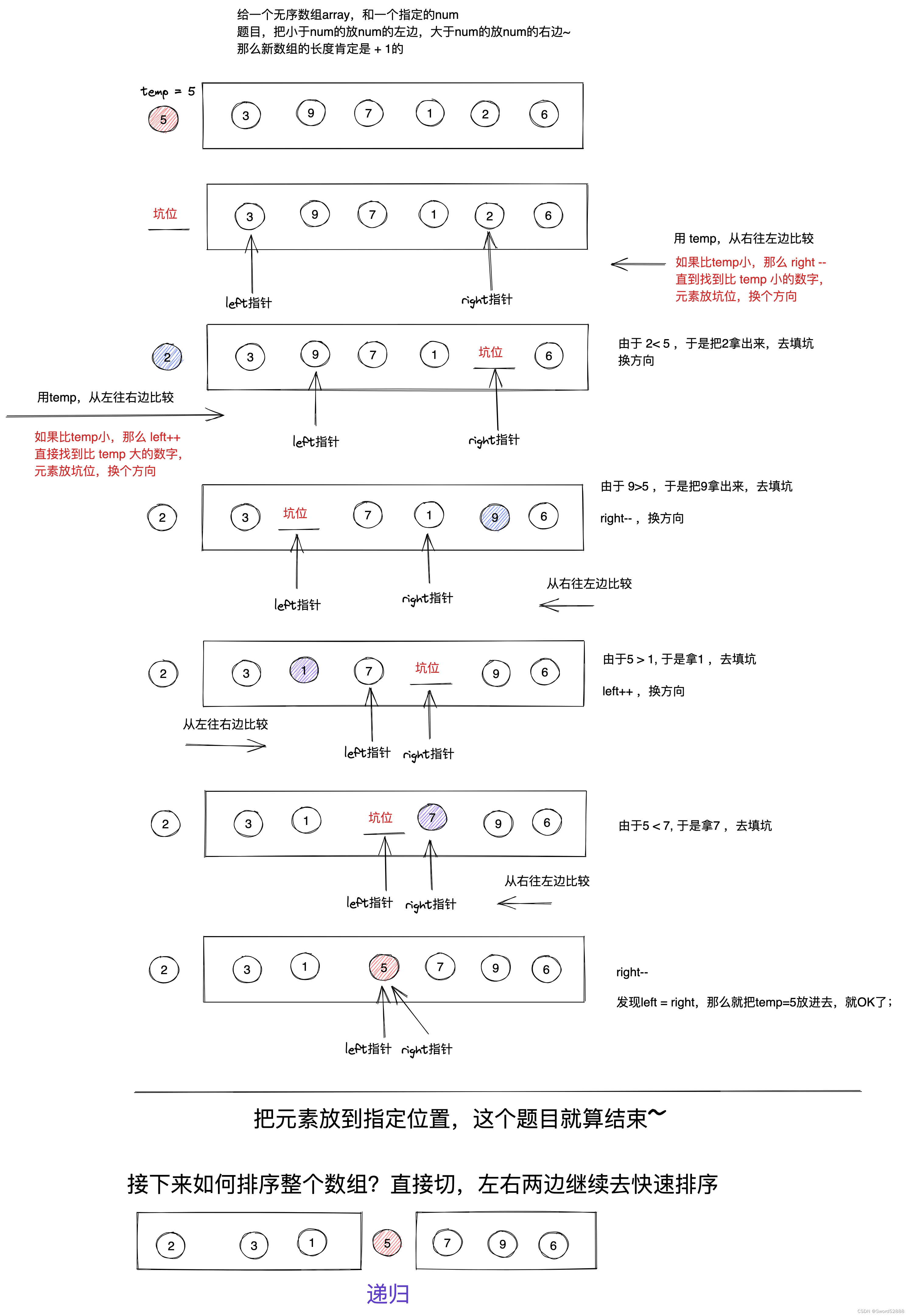
4.4.1 代码
/*** 快速排序算法* @param nums 待排序的数组* @param beginIndex 排序起始索引* @param endIndex 排序结束索引*/
private static void quickSort(int[] nums, int beginIndex, int endIndex) {if (beginIndex >= endIndex) {return; // 递归终止条件:当开始索引大于等于结束索引时,表示已经完成排序}int mid = getMid(nums, beginIndex, endIndex); // 获取中间索引,用于分割数组quickSort(nums, beginIndex, mid - 1); // 对中间索引左侧的数组进行快速排序quickSort(nums, mid + 1, endIndex); // 对中间索引右侧的数组进行快速排序
}/*** 获取分区中的中间元素的索引* @param nums 待排序的数组* @param beginIndex 分区的起始索引* @param endIndex 分区的结束索引* @return 中间元素的索引*/
private static int getMid(int[] nums, int beginIndex, int endIndex) {int target = nums[beginIndex]; // 以数组的起始元素作为基准值int left = beginIndex;int right = endIndex;boolean right2left = true; // 标识位,表示当前从右往左搜索while (right > left) {if (right2left) {while (right > left && nums[right] > target) {right--;}if (right > left) {nums[left] = nums[right]; // 当右侧元素较大时,将右侧元素移到插入位置right2left = false; // 切换为从左往右搜索}} else {while (right > left && nums[left] < target) {left++;}if (right > left) {nums[right] = nums[left]; // 当左侧元素较小时,将左侧元素移到插入位置right2left = true; // 切换为从右往左搜索}}}nums[left] = target; // 将基准值放入插入位置,完成一轮交换return left;
}
4.4.2 复杂度
时间复杂度: N Log N (每个元素找到中间位置的,需要 LogN 时间,N个元素就是NLogN)
空间复杂度:N Log N (递归调用,需要栈空间)
最差时间复杂度:N ^ 2 ( 比如正序数组 [1,2,3,4,5] )

稳定性:不稳定的

4.5 堆排序
(思路:最大放上面,然后与最后元素交换,继续建堆)
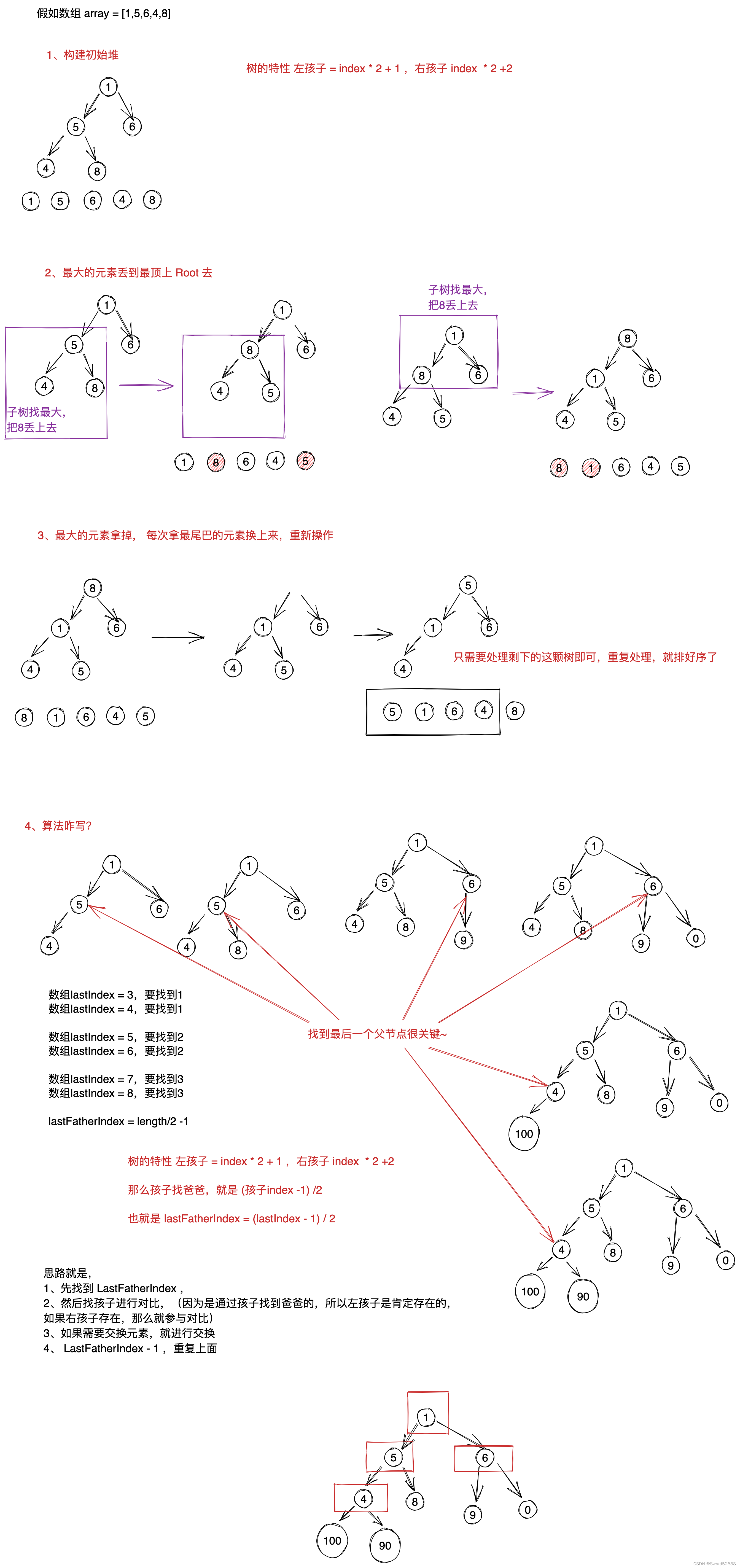
4.5.1 代码
/*** 堆排序算法* @param nums 待排序的数组* @param beginIndex 排序的起始索引* @param endIndex 排序的结束索引*/
private static void heapSort(int[] nums, int beginIndex, int endIndex) {if (beginIndex >= endIndex) {return; // 当开始索引大于等于结束索引时,排序完成}for (int i = endIndex; i >= beginIndex; i--) {createHeap(nums, i); // 构建最大堆swap(nums, 0, i); // 将最大元素移到数组末尾}
}/*** 构建最大堆* @param nums 待构建的数组* @param endIndex 当前堆的结束索引*/
private static void createHeap(int[] nums, int endIndex) {int lastFatherIndex = (endIndex - 1) / 2;for (int i = lastFatherIndex; i >= 0; i--) {int biggestIndex = i;int leftChildIndex = i * 2 + 1;int rightChildIndex = i * 2 + 2;if (leftChildIndex <= endIndex) {biggestIndex = nums[biggestIndex] > nums[leftChildIndex] ? biggestIndex : leftChildIndex;}if (rightChildIndex <= endIndex) {biggestIndex = nums[biggestIndex] > nums[rightChildIndex] ? biggestIndex : rightChildIndex;}swap(nums, biggestIndex, i); // 调整堆,确保最大元素位于堆顶}
}/*** 交换数组中两个元素的位置* @param nums 数组* @param i 索引1* @param j 索引2*/
private static void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;
}
4.5.2 复杂度
时间复杂度: N Log N (每个元素都要构建1次堆,需要 LogN 时间,N个元素就是NLogN,任何情况下都一样)
空间复杂度:1 (原地排序)
最差时间复杂度:N ^ 2 ( 比如正序数组 [1,2,3,4,5] )
稳定性:不稳定的

4.6 归并排序
递归思路,左右两边排序好了,就已经排序好了

4.6.1 代码
// 归并排序的主方法
private static void mergeSort(int[] nums, int beginIndex, int endIndex) {// 如果起始索引大于等于结束索引,表示只有一个元素或没有元素,不需要排序if (beginIndex >= endIndex) {return;}// 计算数组的中间索引int mid = beginIndex + (endIndex - beginIndex) / 2;// 递归排序左半部分mergeSort(nums, beginIndex, mid);// 递归排序右半部分mergeSort(nums, mid + 1, endIndex);// 合并左右两部分merge(nums, beginIndex, mid, endIndex);
}// 合并函数,用于将左右两部分合并成一个有序的数组
private static void merge(int[] nums, int beginIndex, int mid, int endIndex) {int left = beginIndex;int right = mid + 1;int[] newArrays = new int[endIndex - beginIndex + 1];int newArraysIndex = 0;// 比较左右两部分的元素,将较小的元素放入新数组while (left <= mid && right <= endIndex) {newArrays[newArraysIndex++] = nums[left] <= nums[right] ? nums[left++] : nums[right++];}// 将剩余的左半部分元素复制到新数组while (left <= mid) {newArrays[newArraysIndex++] = nums[left++];}// 将剩余的右半部分元素复制到新数组while (right <= endIndex) {newArrays[newArraysIndex++] = nums[right++];}// 将合并后的新数组复制回原数组for (int i = 0; i < newArrays.length; i++) {nums[beginIndex + i] = newArrays[i];}
}
4.6.2 复杂度
时间复杂度: N Log N (每个元素都要递归,需要 LogN 时间,N个元素就是NLogN,任何情况下都一样)
空间复杂度:N
稳定性:稳定的
4.7 希尔排序
思路:直接插入排序的升级版(分段式插入排序)
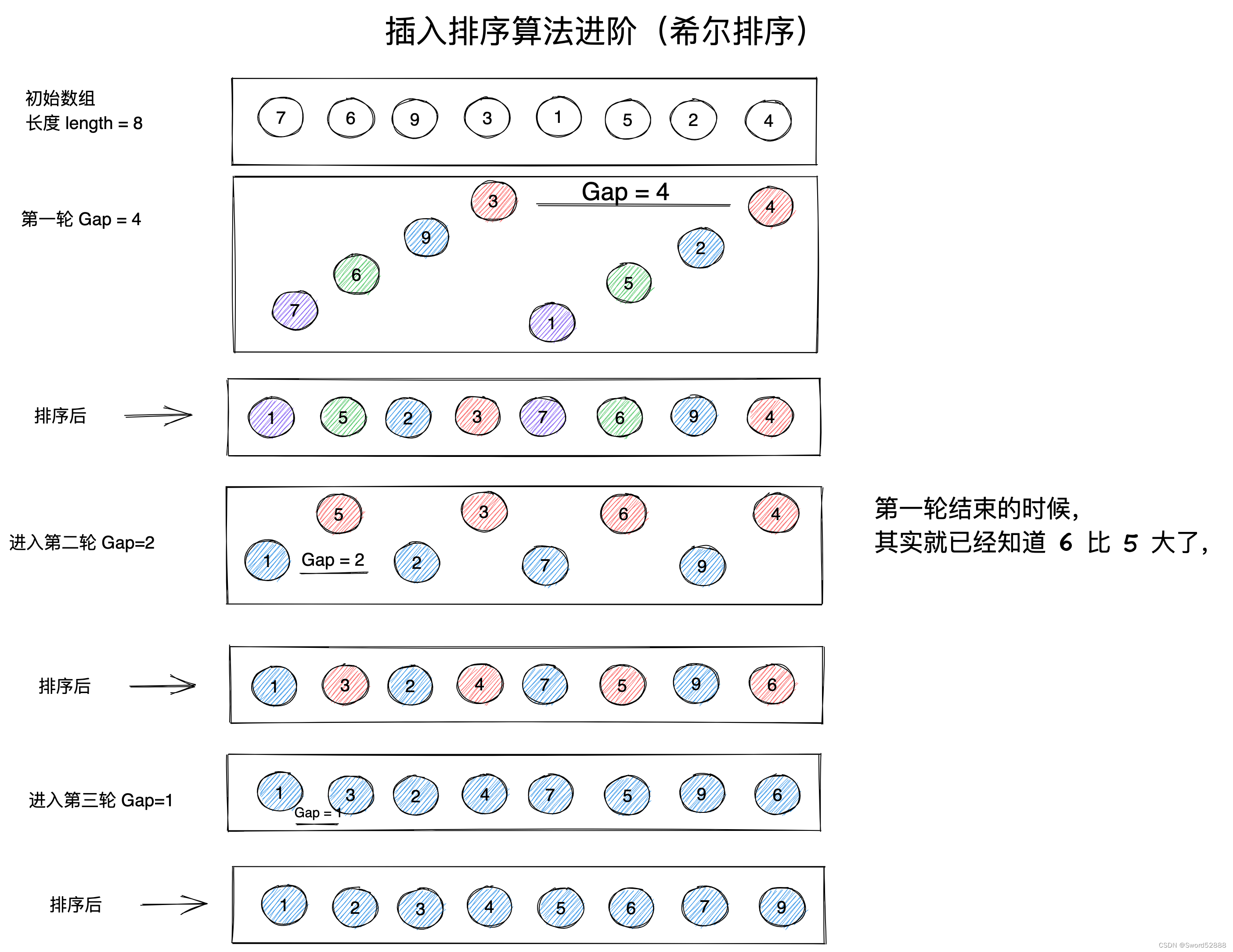
4.7.1 代码
private static void quickSort(int[] nums) {
// int gap = nums.length / 2;
// while (gap > 0) {for (int i = 1; i < nums.length; i++) {int temp = nums[i];int j;for (j = i - 1; j >= 0 && temp < nums[j]; j--) {nums[j + 1] = nums[j];}nums[j + 1] = temp;}
// gap = gap / 2;
// }}// 把上面的快速排序改成shell排序,只需要把间隔1 改成gapprivate static void shellSort(int[] nums) {int gap = nums.length / 2;while (gap > 0) {for (int i = gap; i < nums.length; i++) {int temp = nums[i];int j;for (j = i - gap; j >= 0 && temp < nums[j]; j = j - gap) {nums[j + gap] = nums[j];// 如果当前元素比待插入元素大,将当前元素向后移动}nums[j + gap] = temp; // 因为上边 j=j-gap退出的时候,j已经被剪掉1次了,可能小于0了}gap = gap / 2;}}4.7.2 复杂度
时间复杂度: N Log N
空间复杂度:1
稳定性:稳定的
相关文章:

排序算法的空间复杂度和时间复杂度
一、排序算法的时间复杂度和空间复杂度 排序算法 平均时间复杂度 最坏时间复杂度 最好时间复杂度 空间复杂度 稳定性 冒泡排序 O(n) O(n) O(n) O(1) 稳定 直接选择排序 O(n) O(n) O(n) O(1) 不稳定 直接插入排序 O(n) O(n) O(n) O(1) 稳定 快速排序 O(n…...

【电路笔记】-基尔霍夫电路定律
基尔霍夫电路定律 文章目录 基尔霍夫电路定律1、框架和定义2、基尔霍夫电流定律3、基尔霍夫电压定律4、基尔霍夫定律应用5、基尔霍夫定律的局限性6、总结 在本文中,将介绍最基本、最重要的电路定律之一。 这些法律由德国医生古斯塔夫基尔霍夫 (Gustav Kirchoff) 于 …...

从零开始搭建React+TypeScript+webpack开发环境-基于axios的Ajax请求工具
什么是axios axios是一款基于Promise的HTTP客户端,适用于浏览器和Node.js环境。它的特点包括: 支持浏览器和Node.js环境。支持Promise API。支持拦截请求和响应。支持取消请求。自动转换JSON数据。支持CSRF保护。 使用axios可以更方便地发送HTTP请求&…...
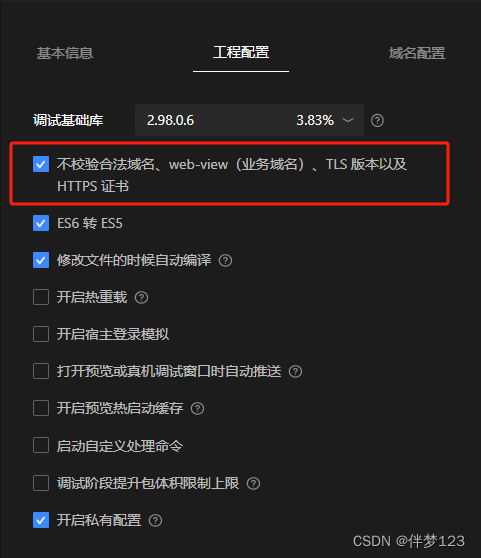
【uniapp小程序下载】调用uni.uploadfile方法在调试工具里是没有问题的,但是线上版本和体验版就调用不成功,真机调试也没问题
把你的下载地址前缀添加到合法域名就解决了 在调试工具里成功了是因为勾选了下面这项 下面是我的下载并打开函数 methods: {// 下载downloadFileFn(data) {if (this.detailsObj.currentUserBuy) {uni.downloadFile({// data是路径url: https:// data,success(res) {//保存到本…...

chatGLM中GLM设计思路
GLM是结合了MLM和CLM的一种预训练方式,其中G为general;在GLM中,它不在以某个token为粒度,而是一个span(多个token),这些span之间使用自编码方式,而在span内部的token使用自回归的方式…...

卡牌游戏类型定制开发微信卡牌小程序游戏
卡牌类型的游戏开发具有一些独特的特点和挑战,以下是一些主要的特点: 卡牌设计和平衡:卡牌游戏的核心是卡牌设计和平衡。开发团队需要设计各种卡牌,确保它们在游戏中相互平衡,以便提供有趣的游戏体验。卡牌的特性、效…...

web —— css(1)
Web —— css基础 1. CSS样式表2. CSS的三种引入方式3. CSS 语法4. CSS 选择器4.1 元素选择器4.2 类选择器4.3 ID选择器4.4 属性选择器4.5 后代选择器4.6 子元素选择器4.7 伪类选择器4.8 分组选择器 5. 颜色和字体6. 显示方式display7. 盒子模型7.1 盒子模型 - 外边距塌陷7.2 盒…...

站群服务器的特性和好处是什么
站群服务器的特性和好处是什么 站群服务器的特性是什么?站群服务器是一种为一个网站或多个网站配置独立IP的服务器。因而相比一般的服务器,站群服务器最大的特性就是IP数量是非常的多。那么租用站群服务器使用有什么好处呢? 多网站优化 大…...

竞赛 行人重识别(person reid) - 机器视觉 深度学习 opencv python
文章目录 0 前言1 技术背景2 技术介绍3 重识别技术实现3.1 数据集3.2 Person REID3.2.1 算法原理3.2.2 算法流程图 4 实现效果5 部分代码6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习行人重识别(person reid)系统 该项目…...

软件设计模式的意义
软件设计模式的意义 所有开发人员都应该接触过软件设计模式这个概念,看过《设计模式-可复用的对象软件的基础》这本书,在面试中都被问过: 你用过哪些设计模式这种问题。但很大可能也就仅此而已了。 为什么好像只能从框架中找到设计模式的应用…...
vue基础知识十八:说说你对keep-alive的理解是什么?
一、Keep-alive 是什么 keep-alive是vue中的内置组件,能在组件切换过程中将状态保留在内存中,防止重复渲染DOM keep-alive 包裹动态组件时,会缓存不活动的组件实例,而不是销毁它们 keep-alive可以设置以下props属性:…...
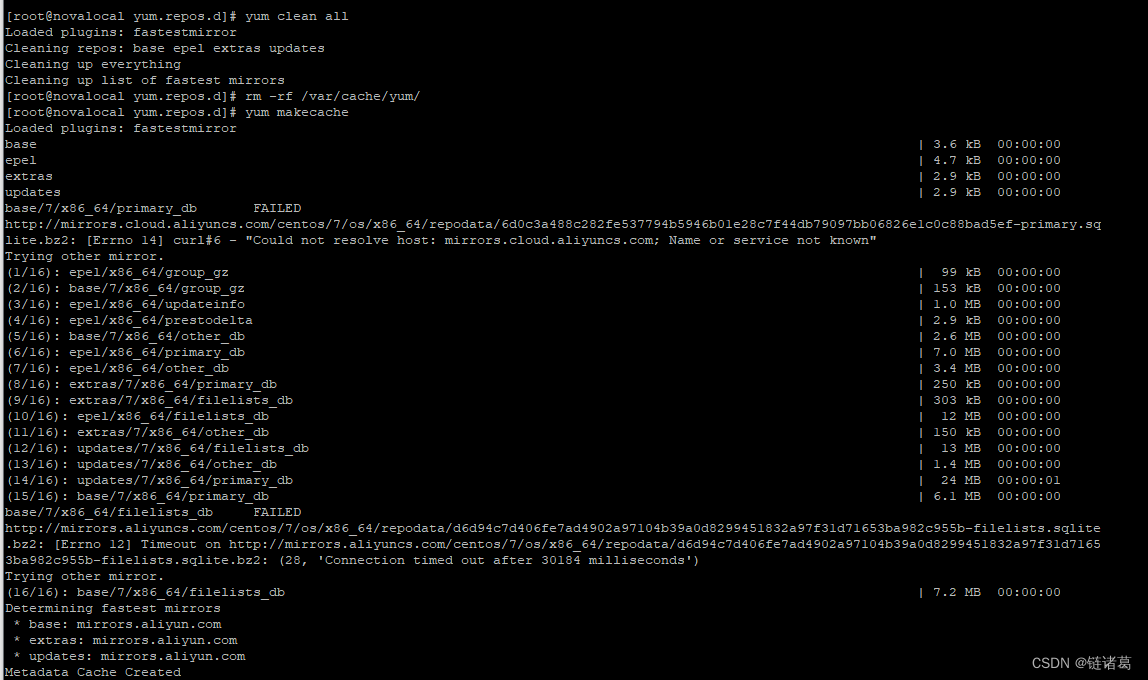
Linux CentOS配置阿里云yum源
一:先备份文件,在配置失败时可以恢复 cd /etc/yum.repos.d mkdir back mv *.repo back 二:下载阿里云yum源 wget -O /etc/yum.repos.d/CentOS-Base.repo https://mirrors.aliyun.com/repo/Centos-7.repo wget -O /etc/yum.repos.d/epel…...

ESP32网络开发实例-Web服务器以仪表形式显示传感器计数
Web服务器以仪表形式显示传感器计数 文章目录 Web服务器以仪表形式显示传感器计数1、应用介绍2、软件准备3、硬件准备4、代码实现4.1 Web页面文件4.2 Web服务器代码实现在本文中,我们将介绍使用服务器发送事件 (SSE) 构建 ESP32 仪表 Web 服务器。服务器将自动向所有连接的网络…...

@Bean有哪些属性
直接看原文 原文链接:Spring中bean标签的作用和属性的详解-CSDN博客 -------------------------------------------------------------------------------------------------------------------------------- Bean的配置一般都在XML文件进行配置Bean相关包为:or…...

【Qt之绘制兔纸】
效果 代码 class drawRabbit: public QWidget { public:drawRabbit(QWidget *parent nullptr) : QWidget(parent) {}private:void paintEvent(QPaintEvent *event) {QPainter painter(this);painter.setRenderHint(QPainter::Antialiasing, true);// 绘制兔子的耳朵painter.s…...
JS+CSS随机点名详细介绍复制可用(可自己添加人名)
想必大家也想拥有一个可以随机点名的网页,接下来我为大家介绍一下随机点名,可用于抽人,哈哈 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title><style>* {margin: 0;…...

西瓜书笔记
周志华老师亲讲-西瓜书全网最详尽讲解-1080p高清原版《机器学习初步》 周志华机器学习(西瓜书)学习笔记(持续更新) 周志华《Machine Learning》学习笔记 绪论 基本术语 数据集(data set):一堆…...

学算法常用刷题网站
学算法常用刷题网站 AcWing : 北大报送生,NOI金牌得主—yxc创办 CodeForces: 简称CF,俄罗斯的网站 hduoj: 杭州电子科技大学的在线评测系统 vjudge:用户可以自己举办比赛 POJ: 北京大学的在线评测系统 洛谷:很火的刷题网站 计蒜客…...
-37)
hdlbits系列verilog解答(always块条件语句)-37
文章目录 一、问题描述二、verilog源码三、仿真结果一、问题描述 Verilog 有一个三元条件运算符 ( ? : ) 很像 C语言: (condition ? if_true : if_false) 这可用于根据一行上的条件(多路复用器!)选择两个值之一,而无需在组合 always 块中使用 if-then。 举例: (0…...

智能井盖生产商家,万宾科技井盖传感器产品详情
市政府管理水平决定城市人民幸福程度,所以在智慧城市推进过程中,市政府也在加快城市信息基础设施建设,希望提高公共服务水平,以此来满足城市居民的需求,进一步推进城市信息化智能化发展。作为城市生命线的一个组成部分…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
