洛谷 P1020 [NOIP1999 普及组] 导弹拦截【一题掌握三种方法:动态规划+贪心+二分】最长上升子序列LIS解法详解
P1020 [NOIP1999 普及组] 导弹拦截
- 前言
- 题目
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 题目分析
- 注意事项
- 代码
- 动态规划(NOIP要求:时间复杂度O(n^2^))
- 贪心+二分(O(nlgn))
- 后话
- 额外测试用例
- 样例输入 #1
- 样例输出 #1
- 样例输入 #2
- 样例输出 #2
- 王婆卖瓜
- 参考来源
前言
再做几题动态规划我们就去做图搜索,另外最近要期中考因为还是需要绩点的,所以断更几天。期中考后应该就开始图搜索算法啦!
隐约记得这题当作期末或者期中考的题目,应该是算法的,至少当时我是没有做出来的,现在我凭自己的实力做出来了O(n2),虽然没有很快做出来卡了好久,但是至少进步是很明显的!然后又学习了一下贪心的思想也是做出来O(lgn)!希望跟着我刷题的宝子们跟着我的进度也能有大的进步!
题目
题目描述
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度,计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
输入格式
一行,若干个整数,中间由空格隔开。
输出格式
两行,每行一个整数,第一个数字表示这套系统最多能拦截多少导弹,第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
样例 #1
样例输入 #1
389 207 155 300 299 170 158 65
样例输出 #1
6
2
提示
对于前 50 % 50\% 50% 数据(NOIP 原题数据),满足导弹的个数不超过 1 0 4 10^4 104 个。该部分数据总分共 100 100 100 分。可使用 O ( n 2 ) \mathcal O(n^2) O(n2) 做法通过。
对于后 50 % 50\% 50% 的数据,满足导弹的个数不超过 1 0 5 10^5 105 个。该部分数据总分也为 100 100 100 分。请使用 O ( n log n ) \mathcal O(n\log n) O(nlogn) 做法通过。
对于全部数据,满足导弹的高度为正整数,且不超过 5 × 1 0 4 5\times 10^4 5×104。
此外本题开启 spj,每点两问,按问给分。
upd 2022.8.24 \text{upd 2022.8.24} upd 2022.8.24:新增加一组 Hack 数据。
题目分析
抛开第二问,我们先来关于第一问,也就是第一行的输出。
题目第一问很明显是一个最长非递增子序列的计算或者说最长非严格递减子串。我给出了两个方法,一个是动态规划,但是由于我的技术不精或者说确实没办法,只能达到O(n2)。另一种是贪心+二分,就可以达到O(nlgn)。
首先介绍一下动态规划方法,与我前面的挖地雷类似,首先找到数值变化的点在哪:显然是找到一个更小的值可以加到这个非递增子序列上。但是我们需要找到最好的值,所以我们建立一个f数组,用来存储当前节点的最好结果,然后我们遇到下一个点的时候就可以更新包括这个节点的最好结果,如此下去直到最后一个节点,然后遍历整个f数组,找到最好的值输出。具体代码见下方,但是不足是时间复杂度不太行
接着我们思考贪心的算法,贪心好像需要满足一个前提条件局部最优解是全局最优解的一部分,我这里就不证明了(我也不太会)。直接来看贪心的思想。对于每个数,既可以把它接到已有的导弹拦截后面,也可以建立一个新系统。要使子序列数最少,应尽量不建立新序列。另外,应让每个导弹系统的末尾尽可能大,这样能接的数更多。因为一个数若能接到小数后面,必然能接到大数后面,反之则不成立。我们维护一个栈,用来表示最长非递增子序列,根据贪心算法的思想这个栈的维护需要做到以下两点:1.比栈顶小的数直接入栈;2.找到栈里最小的大于该数的元素,将这个元素替换成这个数。又因为这个栈是从大到小排序,所以我们找位置的时候可以使用二分查找来节省时间。代码也是看下方。
接着就是解决第二问的问题,首先需要引入一个Dilworth定理:
Dilworth定理:对于任意有限偏序集,其最大反链中元素的数目必等于最小链划分中链的数目。
换句话讲,最长上升子序列的长度就是能构成的不上升序列的个数。于是系统求个数其实就是求最长递增子序列或者说LIS的长度,然后按照上面的方法修改一下大于和小于等于号就可以了!是不是很奇妙,所以这题还是很有难度的,但凡你不知道这个定理,想要做出来不是一件容易的事情。
注意事项
1.输入没有给定长度的处理办法
C++
int x,n=-1;
while(cin>>x)a[++n]=x;++n;//从0开始,n表示个数int x,n=0;
while(cin>>x)a[++n]=x;//从1开始,n表示个数//不知道为什么while(cin>>a[n++]);不行
C语言
while(~scanf("%d",&a[++n])); --n;
while (scanf("%d", a+(++n)) != EOF) ; --n;
python(待补充)
#有没有帅哥美女知道的评论区告诉我一下
2.注意是最长非严格递减数列,所以是可以包括等于的情况,判断时应该是a[j]>=a[i]
3.二分法while里面记得判断条件是a[i]>f[mid],有个笨蛋写成a[i]>f[point]了。
代码
动态规划(NOIP要求:时间复杂度O(n2))
NOIP的要求是O(n2),所以我们可以使用动态规划过前十个点的数据
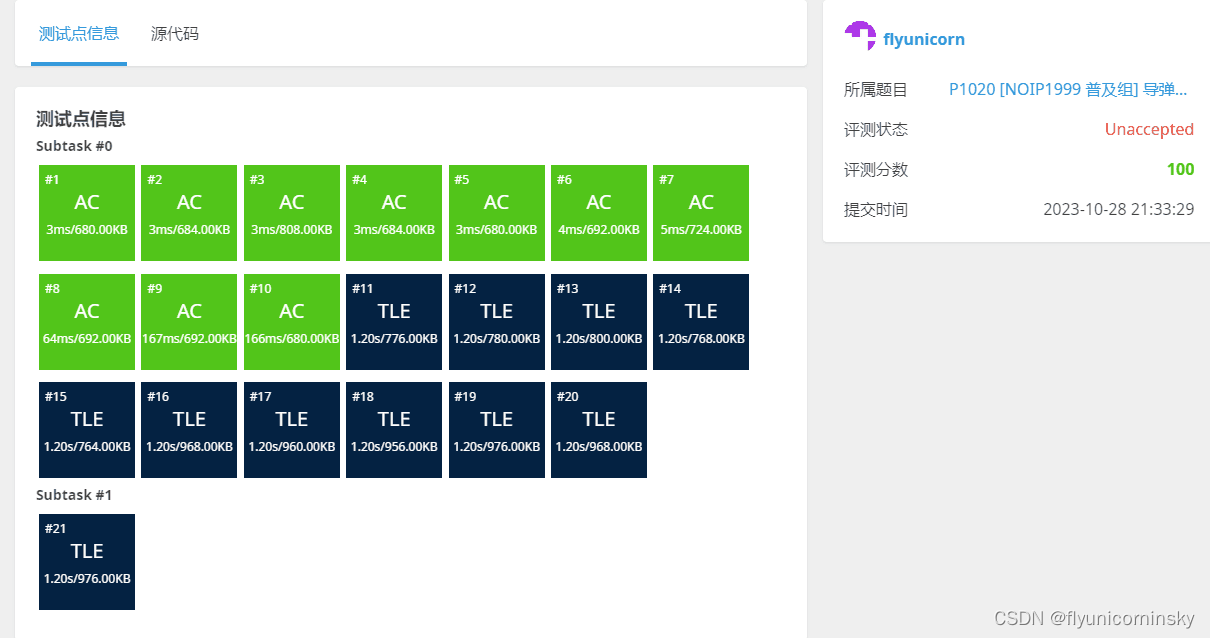
#include<iostream>
using namespace std;
int a[100007]= {0},path[27]= {0},f1[100007]= {0},f2[100007]= {0};
int main()
{int n=-1,maxx=0,minn=0,flag1=0,flag2=0,x;while(cin>>x)a[++n]=x;++n;f1[0]=1;f2[0]=1;for(int i=1; i<n; i++) {maxx=0;minn=0;//每次都要重新初始化for(int j=0; j<i; j++) {if(f1[j]>maxx&&a[i]<=a[j]) {//找到符合条件的最大值maxx=f1[j];}if(f2[j]>minn&&a[i]>a[j]) {minn=f2[j];}}f1[i]=maxx+1;f2[i]=minn+1;}int ans1=0,ans2=0;for(int i=0; i<n; i++) {if(f1[i]>ans1)ans1=f1[i];if(f2[i]>ans2)ans2=f2[i];}cout<<ans1<<endl<<ans2;return 0;
}
贪心+二分(O(nlgn))
本法巧妙利用了贪心的性质,并且用二分法来查找最大值,将时间复杂度打到O(nlgn)。
并且有个偷懒的地方是使用了一个判断函数,将两个计算子串长度的函数合并成一个!
栈还保存了最长上升或递减子序列的列表
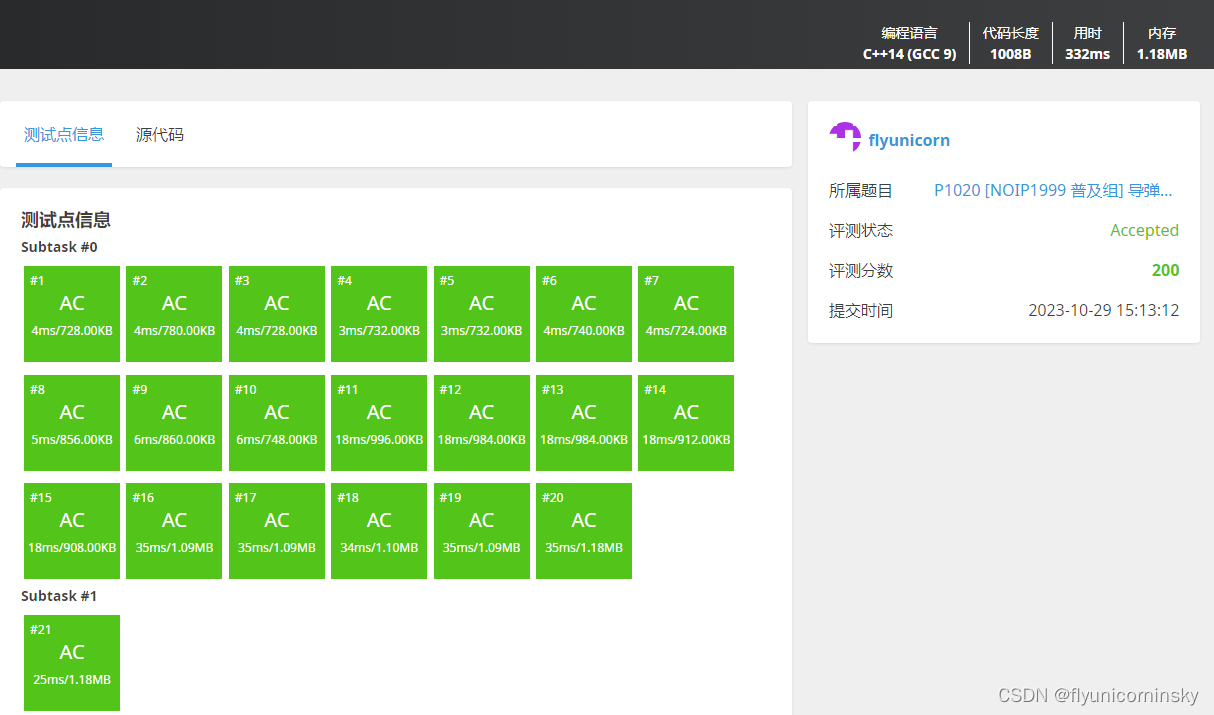
噔噔噔!代码闪亮登场!
#include<iostream>
using namespace std;int a[100007]= {0},f[100007]= {0};
void test(int f[],int x){//没有用就是用来测试的 for(int i= 1; i<=x;i++){cout<<f[i]<<" ";}cout<<endl;
}
bool relation(int x,int y,int rela)//用来返回判断值的
{if(rela==1) {return x>y;} elsereturn x<=y;
}
int Lg_sequence(int n,int rela)//计算相反的两个最长子串
{int f[100007]= {0};int point=1;f[1]=a[0];for(int i = 1 ; i < n ; i ++) {if(relation(a[i],f[point],rela)) {//符合子串直接入栈 f[++point]=a[i];} else {int l = 1, r = point;while (l < r) {//找到大于该值的最小的栈值 int mid = (l + r) >> 1;if (relation(a[i],f[mid],!rela)) {r = mid;} else {l = mid + 1;}}f[l] = a[i];}}return point;
}
int main()
{int n=-1,maxx=0,minn=0,point=1,x;while(cin>>x)a[++n]=x;++n;//n表示数组长度 cout<<Lg_sequence(n,0)<<endl<<Lg_sequence(n,1);return 0;
}
后话
额外测试用例
因为太笨获得了两个测试用例
样例输入 #1
330 309 267 287 315 380 365 363 364 351 316 381 355 372 289 284 356 299 369 361 327 372 360 282 327 280 258 293 258 254 298 320 324 314 273 340 251 324 327 339 270 248 275 318 321 283 293 341 247 321 318 270 328 322 294 299 259 304 302 286 287 239 333 300 269 240 269 275 296 292 254 308 325 285 218 282 221 288 238 307 212 263 316 300 264 278 215 304 306 296 218 206 225 206 266 250 288 208 241 297 264 211 285 294 236 206 292 215 249 195 206 202 198 276 258 199 192 207 195 261 253 212 206 214 269 234 254 250 196 246 244 227 229 238 194 221 192 243 181 233 180 242 206 247 223 195 187 210 181 176 214 201 209 207 231 222 199 217 212 222 197 168 217 195 193 216 163 203 163 230 206 201 153 184 177 193 174 189 175 155 148 197 184 201 169 155 182 166 156 202 204 193 143 199 167 194 174 195 181 171 163 170 173 169 184 160 130 132 166 128 160 149 140 182 144 127 140 175 134 175 146 169 159 176 152 118 131 120 156 119 141 144 121 146 116 160 136 116 123 135 109 158 127 115 127 148 116 126 140 109 129 122 123 120 109 114 134 98 95 133 108 108 124 115 99 92 97 132 106 116 115 120 116 123 91 94 107 115 114 110 98 81 94 109 114 86 92 97 105 107 94 98 79 93 83 96 70 71 88 71
样例输出 #1
69
11
样例输入 #2
90 103 99 83 102 70 86 70 99 71
样例输出 #2
5
3
王婆卖瓜
感觉有收获或者想跟上我的进度刷题的,可以点个关注,或者点赞收藏评论都可以!
参考来源
NOIP 1999 普及组
洛谷题目-传送门
参考材料-TernaryTree
相关文章:

洛谷 P1020 [NOIP1999 普及组] 导弹拦截【一题掌握三种方法:动态规划+贪心+二分】最长上升子序列LIS解法详解
P1020 [NOIP1999 普及组] 导弹拦截 前言题目题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示题目分析注意事项 代码动态规划(NOIP要求:时间复杂度O(n^2^))贪心二分(O(nlgn)) 后话额外测试用例样例输入 #1…...

golang的管道阻塞问题
package mainimport ("fmt""sync"//"time" ) var wg sync.WaitGroup func writeData(intchan chan int){defer wg.Done()for i : 1; i < 9; i {intchan<-ifmt.Println("写入的数据为:",i)//time.Sleep(time.Seco…...

用HTML + javaScript快速完成excel表格信息除重并合并
今天突然接到一个工作,要把两个存储在.xls的主体信息表,除重后合并成一个主体信息表,并且补充主体类型和所在县区这两列信息。 完成这项工作的方法有很多,如果信息表中的信息量不大的话,手工处理一下也行,如…...

高性能网络编程 - The C10M problem
文章目录 Pre概述回顾C10K实现C10M的挑战思路总结 Pre 高性能网络编程 - The C10K problem 以及 网络编程技术角度的解决思路 概述 在接下来的10年里,因为IPv6协议下每个服务器的潜在连接数都是数以百万级的,单机服务器处理数百万的并发连接࿰…...
java计算机毕业设计SpringBoot在线答疑系统
项目介绍 本文从学生的功能要求出发,建立了在线答疑系统,系统中的功能模块主要是实现管理员权限;首页、个人中心、学生管理、教师管理、问题发布管理、疑难解答管理。教师权限:首页、个人中心、疑难解答管理、试卷管理、试题管理…...
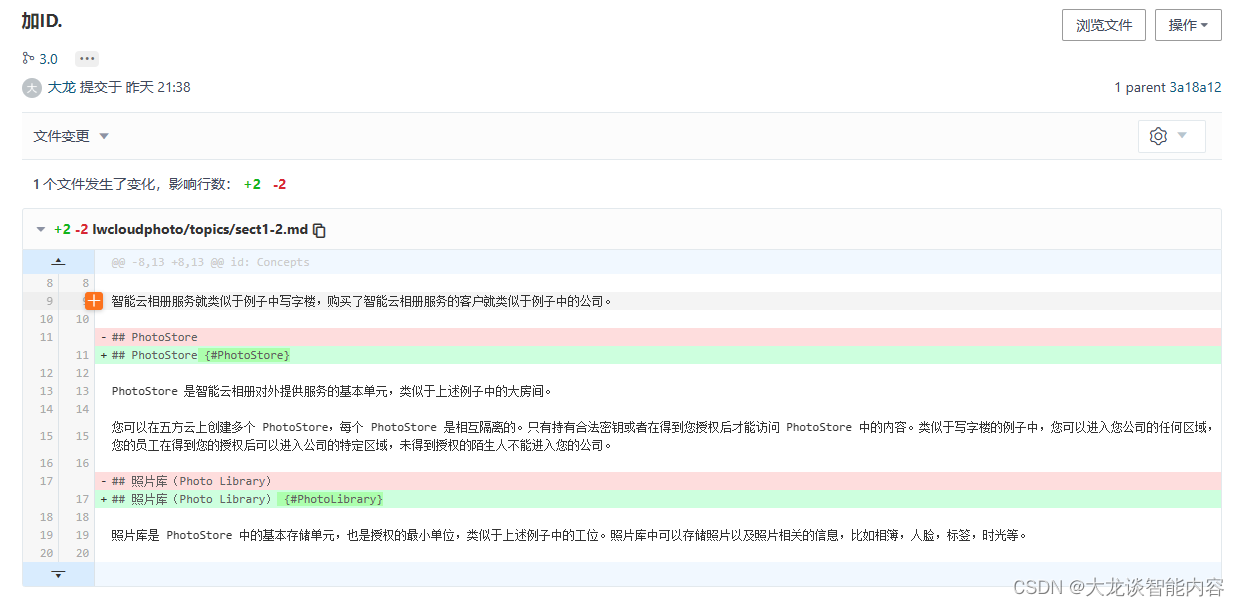
Doc as Code (4):使用Git做版本管理,而不是使用目录做版本管理
▲ 搜索“大龙谈智能内容”关注GongZongHao▲ 在引入版本管理工具之前,文档工程师使用文件系统提供的功能来管理文件。大家是这样工作的: 文件按照分类放在不同的目录里,使用编辑器(如:MS Word)打开文档进…...

【Codeforces】 CF1870E Another MEX Problem
题目链接 CF方向 Luogu方向 题目解法 解法1 考虑优化 d p dp dp 转移次数,即只转移有用的区间 不难发现, m e x ( l , r ) m e x ( l 1 , r ) mex(l,r)mex(l1,r) mex(l,r)mex(l1,r) 或 m e x ( l , r ) m e x ( l , r − 1 ) mex(l,r)mex(l,r-1…...

【Objective-C】Objective-C汇总
方法定义 参考:https://www.yiibai.com/objective_c/objective_c_functions.html Objective-C编程语言中方法定义的一般形式如下 - (return_type) method_name:( argumentType1 )argumentName1 joiningArgument2:( argumentType2 )argumentName2 ... joiningArgu…...

怎么查找性别为女性的不同学历层次不同学位以及所有人不同职务职称的人数
怎么查找性别为女性的不同学历层次不同学位以及所有人不同职务职称的人数 需求分析: 1.统计性别为女性的所获学位下不同学历层次的人数 2.统计不同职务职称的不同学位和学历层次的人数代码 def cal_xuewei_number(self):# 读取表格文件table pd.read_excel("…...

浅谈Elasticsearch查询和搜索
Elasticsearch查询和搜索 Elasticsearch是一个分布式、实时的搜索和分析引擎,广泛应用于全文搜索、日志分析、实时数据分析等场景。Elasticsearch提供了丰富的查询和搜索功能,如查询DSL、过滤、排序、分页、高亮和聚合等。本文将详细介绍如何在Elastics…...

SLAM从入门到精通(被忽视的基础图像处理)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 工业上用激光slam的多,用视觉slam的少,这是大家都知道的常识。毕竟对于工业来说,健壮和稳定是我们必须要考虑的…...
【C++】继承详解
本篇要分享的内容是关于继承的内容哼哼哼啊啊啊啊啊啊啊啊啊啊啊啊啊啊 以下为本篇目录 目录 1.简单了解继承 2.继承的简单定义 3.继承简单使用 4.继承方式 4.1基类的privat 4.2基类的protected 4.3不可见与private的区别 5.父子类对象赋值转换 6.继承的作用域 7.子…...

react:swr接口缓存
useSWR 是一个 React Hooks,是 HTTP 缓存库 SWR 的核心方法之一。SWR 是一个轻量级的 React Hooks 库,通过自动缓存数据来实现 React 的数据获取。 第一个参数是被缓存的数据的 key, 第二个参数是一个函数,该函数返回数据或者一个…...
2023-11 | 短视频批量下载/爬取某个用户的所有视频 | Python
这里以鞠婧祎的个人主页为demo https://www.douyin.com/user/MS4wLjABAAAACV5Em110SiusElwKlIpUd-MRSi8rBYyg0NfpPrqZmykHY8wLPQ8O4pv3wPL6A-oz 【2023-11-4 23:02:52 星期六】可能后面随着XX的调整, 方法不再适用, 请注意 找到接口 找到https://www.douyin.com/aweme/v1/web/…...

【JAVA学习笔记】66 - 本章作业(IO流)
项目代码 https://github.com/yinhai1114/Java_Learning_Code/tree/main/IDEA_Chapter19/src/com/yinhai/homework 1.使用File类和FileWriter类 (1)在判断e盘下是否有文件夹mytemp,如果没有就创建mytemp public class Homework01 {public static void main(String…...
vscode中 vue3+ts 项目的提示失效,volar插件失效问题解决方案
文章目录 前情提要bug回顾解决方案最后 前情提要 说起来很耻辱,从mac环境换到window环境,vscode的配置都是云端更新过来的,应该是一切正常才对,奇怪的是我的项目环境出现问题了,关于组件的ts和追踪都没有效果ÿ…...
Elasticsearch:在 ES|QL 中使用 DISSECT 和 GROK 进行数据处理
目录 DISSECT 还是 GROK? 或者两者兼而有之? 使用 DISSECT 处理数据 Dissect pattern 术语 例子 DISSECT 关键修饰符 右填充修饰符 (->) 附加修饰符 () 添加顺序修饰符( 和 /n) 命名的跳过键(?…...

基于自适应自回归模型的高级人工智能概念及其实现
基于自适应自回归模型的高级人工智能概念及其实现 摘要:一、引言:二、方法:三、讨论:四、结论:草稿实现计算摘要: 在人工智能研究领域中,预测未来的信息往往会遇到信息不明确的问题,尤其是在自回归模型中,这一问题尤为突出。本研究提出一个新颖的假设,将能自主解决信…...
windows的mysql启动错误,查看windows日志
1、点击左下角开始按钮,计算机上右键,点击【管理】。 2、在计算机管理界面依次找到【系统工具】,选择【时间查看器】,打开【windows日志】,点击【应用程序】 3、在右侧找到,最新的mysql错误信息。双击查看。…...
centos7部署Canal与Canal集成使用
1、简介 canal [kə’nl],译意为水道/管道/沟渠,主要用途是基于 MySQL 数据库增量日志解析,提供增量数据订阅和消费 早期阿里巴巴因为杭州和美国双机房部署,存在跨机房同步的业务需求,实现方式主要是基于业务 trigge…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
