数据结构-Prim算法构造无向图的最小生成树
引子:
无向图如果是一个网,那么它的所有的生成树中必有一颗生成树的边的权值之和是最小的,我们称
这颗权值和最小的树为:“最小生成树”(MST)。
其中,一棵树的代价就是树中所有权值之和。
而在现实中,最小生成树的概念可以用来解决很多实际问题,例如,在n个城市之间建立交通网,
那么哪一条路径是最短的呢?就可以用最小生成树来解决。
算法思想:
设G = (V,E)为以连通网,其中V为顶点集合,E为带权边集合。
设置两个新集合U和T:
U用于存放最小生成树的顶点,T用于存放最小生成树的边。
令集合的初值为:{u0}(假设构造最小生成树时,从顶点u0出发。)
集合T的初值为{}。
从所有u∈U,v∈V-U的边(u,v)中,选取最小权值的边(u0,v0),将顶点v0加入集合U中,将边
(u0,v0)加入集合T中。
如此不断重复,知道U = V,最小生成树构造完成,集合T中包含了最小生成树中的所有边。
分析算法可知:
为了实现Prim算法,需要一个辅助数组closedge以记录从U到V-U具有最小代价的边。
对于closedge数组需要包含两个域:
adjvex和lowcost,其中lowcost = 0表示若顶点v不在生成树上,用closedge.lowcost存放v与生成树
上的另一个顶点的序号所构成边的权值。
adjvex存放与该边相关联的生成树上的另一顶点的序号。
算法生成图
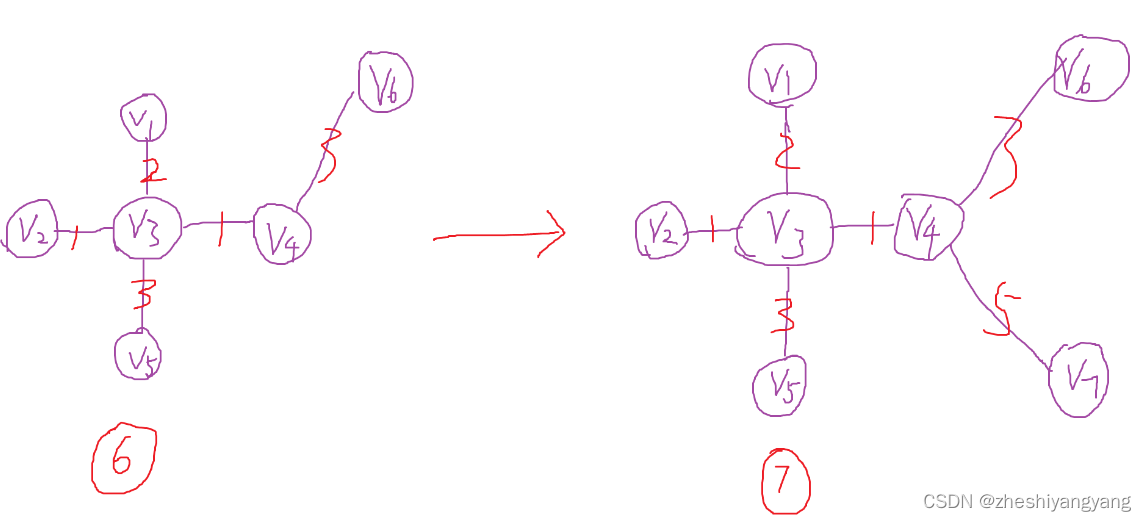
对于下面这个无向图例子来说:

算法的执行过程如下:

代码部分:
#include<stdio.h>
#define MAX 100
typedef struct Mgraph{char vertex[MAX];int arcs[MAX][MAX];int vexnum,arcnum;
}Mgraph;typedef struct Closedge{char adjvex[MAX];int lowcost[MAX];
}Closedge;int LocateVerTex(Mgraph *G,char v)
{int k;for(k=0;k<G->vexnum;k++)if(G->vertex[k] == v)return k;return -1;
}void CreateMgraph(Mgraph *G)
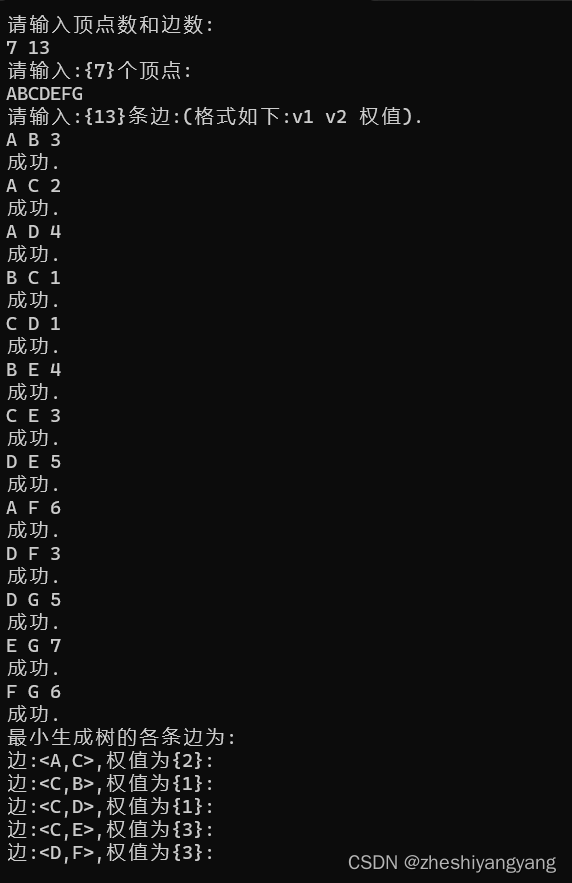
{int i,j,weight,adj1,adj2;char v1,v2;printf("请输入顶点数和边数:\n");scanf("%d %d",&G->vexnum,&G->arcnum);getchar();printf("请输入:{%d}个顶点:\n",G->vexnum);for(i=0;i<G->vexnum;i++)scanf("%c",&G->vertex[i]);getchar();printf("请输入:{%d}条边:(格式如下:v1 v2 权值).\n",G->arcnum);for(i=0;i<G->vexnum;i++){for(j=0;j<G->vexnum;j++){G->arcs[i][j] = 9999;}}for(i=0;i<G->arcnum;i++){scanf("%c %c %d",&v1,&v2,&weight);getchar();adj1 = LocateVerTex(G,v1);adj2 = LocateVerTex(G,v2);if(adj1 == -1 || adj2 == -1){printf("失败.\n");i = i - 1;continue;}else{G->arcs[adj1][adj2] = weight;G->arcs[adj2][adj1] = weight;printf("成功.\n");}}
}int MiniNum(Closedge *closedge,Mgraph *G)
{int j,p = 1,min = 999;for(j=0;j<G->vexnum;j++){if(closedge->lowcost[j] != 0 && closedge->lowcost[j] < min){min = closedge->lowcost[j];p = j;}}return p;
}void MiniTree_Prim(Mgraph *G,char u)
{int i,j,k,num;k = LocateVerTex(G,u);Closedge closedge;for(i=0;i<G->vexnum;i++){if(i!=k){closedge.adjvex[i] = u;closedge.lowcost[i] = G->arcs[k][i];}}closedge.lowcost[k] = 0;printf("最小生成树的各条边为:\n");for(i=1;i<G->vexnum;i++){k = MiniNum(&closedge,G);printf("边:<%c,%c>,权值为{%d}:\n",closedge.adjvex[k],G->vertex[k],closedge.lowcost[k]);closedge.lowcost[k] = 0;for(j=0;j<G->vexnum;j++){if(G->arcs[k][j] < closedge.lowcost[j]){closedge.adjvex[j] = G->vertex[k];closedge.lowcost[j] = G->arcs[k][j];}}}
}int main()
{Mgraph G;CreateMgraph(&G);MiniTree_Prim(&G,'A');return 0;
}验证部分:
相关文章:

数据结构-Prim算法构造无向图的最小生成树
引子: 无向图如果是一个网,那么它的所有的生成树中必有一颗生成树的边的权值之和是最小的,我们称 这颗权值和最小的树为:“最小生成树”(MST)。 其中,一棵树的代价就是树中所有权值之和。 而…...
MFC串口通信(SerialPort)
目录 1、SerialPort类的介绍和使用: (1)、SerialPort类的功能介绍 (2)、SerialPort类提供接口函数的介绍 1)、InitPort函数 2)、控制串口监视线程函数 3)、获取事件,…...

Vim基本使用操作
前言:作者也是初学Linux,可能总结的还不是很到位 Linux修炼功法:初阶功法 ♈️今日夜电波:美人鱼—林俊杰 0:21━━━━━━️💟──────── 4:14 …...

【深蓝学院】手写VIO第8章--相机与IMU时间戳同步--作业
0. 题目 1. T1 逆深度参数化时的特征匀速模型的重投影误差 参考常鑫助教的答案:思路是将i时刻的观测投到world系,再用j时刻pose和外参投到j时刻camera坐标系下,归一化得到预测的二维坐标(这里忽略了camera的内参,逆深…...

Naocs配置中心配置映射List、Map、Map嵌套List等方式
一、配置映射List 1、常规逐个配置方式,示例如下: 代码: @Data @Configuration @ConfigurationProperties(prefix = "list-json-str") public class ConfListByJsonStr implements Serializable, InitializingBean {@ApiModelProperty("映射结果集")…...

如何通过CRM系统进行销售机会管理?
销售机会管理是在销售过程中对潜在客户的精细化管理,销售机会管理的本质是公司用于管理销售机会通用的工具和方法。对于希望建立长期客户关系的现代销售团队来说,CRM客户管理系统是必不可少的工具。那企业如何通过CRM系统进行销售机会管理? …...

解决idea启动tomcat控制台中文乱码
#1.tomcat日志中文乱码# 如图这种情况,一般在idea用tomcat跑一个web项目启动后tomcat日志在控制台打印出来会出现中文乱码的情况 解决方案1:tomcat的日志配置文件的编码修改,找到tomcat安装目录conf下的logging.properties,encod…...

vscode + cmake + opencv example
nice try on macos CMakeLists.txt cmake_minimum_required(VERSION 3.20) #添加OPENCV库 #指定OpenCV版本,代码如下 #find_package(OpenCV 3.3 REQUIRED) #如果不需要指定OpenCV版本,代码如下 find_package(OpenCV REQUIRED)#添加OpenCV头文件 includ…...

day57【动态规划】647.回文子串 516.最长回文子序列
文章目录 647. 回文子串516.最长回文子序列 647. 回文子串 力扣题目链接 代码随想录讲解 题意:给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的…...

分享vmware和Oracle VM VirtualBox虚拟机的区别,简述哪一个更适合我?
VMware和Oracle VM VirtualBox虚拟机的区别主要体现在以下几个方面: 首先两种软件的安装使用教程如下: 1:VMware ESXI 安装使用教程 2:Oracle VM VirtualBox安装使用教程 商业模式:VMware是一家商业公司,而…...

YOLOV5模型运行
1安装包 如果已经有了torch-cuda环境直接在环境下 pip install -r requirements.txt 2解决报错代码 raise ImportError("Failed to initialize: {0}".format(exc)) from exc ImportError: Failed to initialize: Bad git executable. The git executable must be …...

@Autowired和@Resource注解的区别和联系
直接看原文 原文链接: 【精选】Autowired和Resource注解的区别和联系【精选】 ------------------------------------------------------------------------------------------------------------------------------- 先说联系 联系 Autowired和Resource注解都是作为bean…...

设计模式类型
创建型模式 创建型模式(Creational Pattern)对类的实例化过程进行了抽象,能够将软件模块中对象的创建和对象的使用分离。为了使软件的结构更加清晰,外界对于这些对象只需要知道它们共同的接口,而不清楚其具体的实现细节,使整个系…...

Android修行手册-实现利用POI将图片插入到Excel中(文末送书)
点击跳转>Unity3D特效百例点击跳转>案例项目实战源码点击跳转>游戏脚本-辅助自动化点击跳转>Android控件全解手册点击跳转>Scratch编程案例点击跳转>软考全系列 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&…...

低功耗工业RFID设备应用
随着工业自动化的迅速发展,RFID技术也在工业领域得到了广泛的应用,在近距离非接触读写应用时,常常利用低功耗的工业RFID设备来进行识别,下面我们将详细介绍低功耗工业RFID设备的应用。 低功耗工业RFID设备具有功耗低、体积小、重量…...

# Oracle 库常见问题排查
Oracle 库常见问题排查 文章目录 Oracle 库常见问题排查查询数据库的相关信息查看正在执行的语句杀掉正在执行的sql查看未提交的事务查看锁表 查询数据库的相关信息 查看正在执行的语句 SELECT s.sid, s.serial#, s.username, s.status, s.sql_id, s.sql_child_number, sq.sq…...

矩阵乘积的迹对矩阵求导
说明 有时候为了输入方便,B和都代表B的转置。 矩阵的在线计算有个网站可以参考:Matrix Calculus dtr(AB)/dAB 下面用一个例子来证明。 dtr(ABA)/dAABAB 下面用一个例子来证明: 因为我们要求ABA的迹,所以为了简便,我们…...

IP 地址冲突检测工具
IP 冲突是一个术语,用于表示同一网络或子网中尝试使用相同 IP 地址的两个或多个设备的状态,这可能会导致发往特定主机的通信与其他主机混淆,因为两者都使用相同的 IP,为了避免这种情况,某些主机在发生 IP 冲突时会失去…...
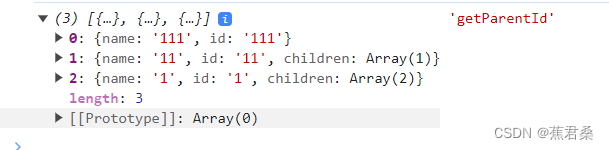
js树形数组遍历练习,扁平化、格式化、获取节点父级
1.树形数组扁平化 数组扁平化的方式很多,这里主要是用递归处理,除此之外还有正则、扩展运算符等等 const list [{name:1,id:1,children:[{name:11,id:11,children:[{name:111,id:111}]},{name:12},]},{name:2,id:2,children:[{name:21,id:21,children:…...
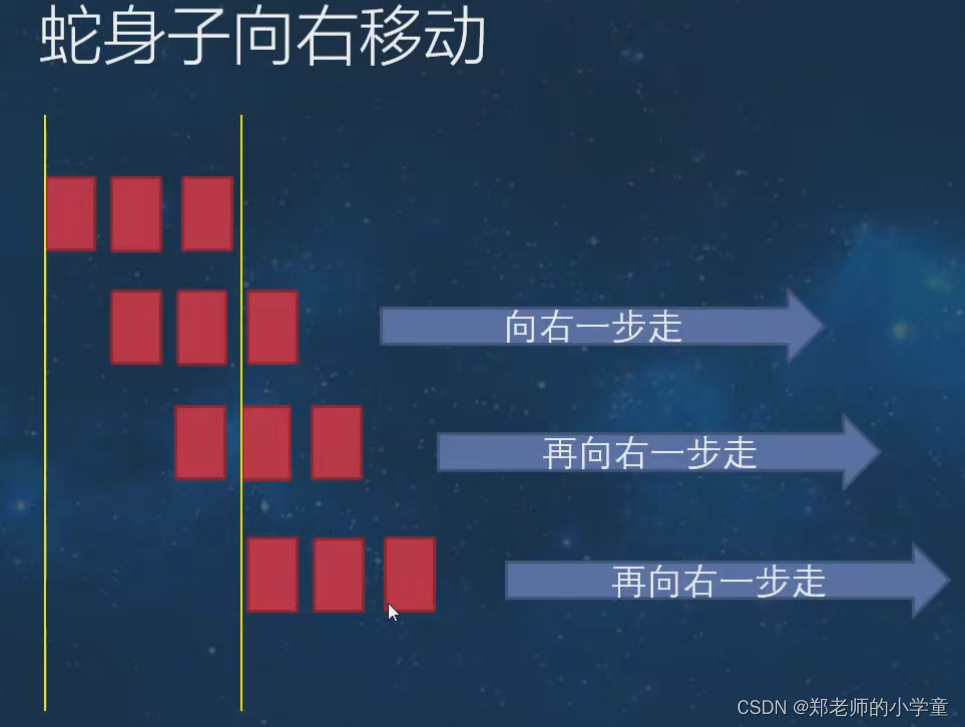
c语言贪吃蛇项目的实现
ncurse的引入 ncurse的概念 ncurse(new curses)是一套编程库,它提供了一系列的函数,以便使用者调用它们去生成基于文本的用户界面。 ncurses是一个能提供功能键定义(快捷键),屏幕绘制以及基于文本终端的图形互动功能的动态库。ncurses用得最多的地方是…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
