【算法练习Day42】买卖股票的最佳时机 III买卖股票的最佳时机 IV

📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:练题
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 买卖股票的最佳时机 III
- 买卖股票的最佳时机 IV
- 总结:
今天这期依旧是买卖股票的专题,两道题难度都是困难,建议先看上一期的文章,搞懂买卖股票的最佳时机I和II再来看本章,可能会更加容易理解题解。
买卖股票的最佳时机 III
123. 买卖股票的最佳时机 III - 力扣(LeetCode)
买卖股票的最佳时机III实际上是I和II的拼凑版本。只能买卖最多两次的含义是,可以买卖一次或者两次,并不是说一定要买卖两次,我们最后取得的答案是买卖一次和买卖两次的最大利润,但其实最终利润如果是买卖一次大,那么买卖第二次时候利润最终会与第一次是相等的数值,这个放在后面说。
dp数组的含义,以及遍历顺序与之前的那期两道题是一样的,只是dp数组的含义得到了扩展,0代表第一次买1代表第一次卖,2代表第二次买,3代表第二次卖,仅此而已。
递推公式:递推公式一共有四个,代表了买卖的第一次和第二次。为什么说它是上一期两道题的结合版本,是因为买卖的第一次我们用到的是I的递推公式,而买卖第二次就是用的II的递推公式!买卖同样的是代表了状态,而不是当天一定买如股票卖出股票,它也可以是以前买入的。简单的再说一次,第一次买股票的递推公式是前一天的拥有的钱和在今天如果买了股票拥有的钱做对比,哪个大取哪个,第一次卖是前一天卖出后的拥有的钱,和如果前一天已经持有股票的话,今天卖了会拥有的利润,取最大值。第二次买卖也是一样不多说了。直接给出四个递推公式。
dp[i][0]=max(dp[i-1][0],-prices[i]);dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]);
dp[i][2]=max(dp[i-1][2],dp[i-1][1]-prices[i]);dp[i][3]=max(dp[i-1][3],dp[i-1][2]+prices[i]);
dp数组的初始化:直接看初始化我们可以知道,第一次买卖再第一天我们都已经分析过了买应该是-prices【i】,因为我们是假设的刚开始手上没有钱初始值是0,不懂得看上一期的文章,卖获得的是0,同一天买卖不赚钱。那第二次买卖我们该如何初始化?我们不妨假设给的数组只有一个数据,也就是只能在第一天买卖,要是这样的想的话,我们第一次卖了之后手里钱和第一次买股票时候钱是一样的,都是0,那么第二次买股票也初始化为-prices【i】,第二次卖也是0。
class Solution {
public:int maxProfit(vector<int>& prices) {vector<vector<int>>dp(prices.size(),vector<int>(4));dp[0][0]=-prices[0];dp[0][1]=0;dp[0][2]=-prices[0];dp[0][3]=0;for(int i=1;i<prices.size();i++){dp[i][0]=max(dp[i-1][0],-prices[i]);dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]);dp[i][2]=max(dp[i-1][2],dp[i-1][1]-prices[i]);dp[i][3]=max(dp[i-1][3],dp[i-1][2]+prices[i]);}return dp[prices.size()-1][3];}
};
这就是这道题的代码了,思路还是比较清晰的,代码也不是十分复杂,但是要想到怎么解,没有做过还是很难的。最后我们来说前面提到的,为什么如果第一次买卖的利润大于第二次买卖,那么第二次买卖到最后也会变成第一次买卖的利润数呢?其实这一点也很好解释,和上一起的第二道题是一样的,我们的从第一个递推公式往后的每一个递推公式都和上一个递推公式有牵连,也就是说这些地推公式里的值,不仅依赖于自己本身的值,也依赖于上一个递推公式所推算出来的最大利润值。所以也就是说各个递推公式一层影响着下一层,最后到了最后一个递推公式,它所推出来的最大利润就一定是两次中的最大利润。
买卖股票的最佳时机 IV
188. 买卖股票的最佳时机 IV - 力扣(LeetCode)
这道题算上是上一道题的进阶版本,最多可以交易几次,是由函数传值影响,并不是直接固定的数值,那么我们还能像上一道题一样手动列出有递推公式吗?其实我们可以借助于循环,帮助我们列出对应数量的递推公式,一共可以买卖k次,那么一定得列出2*k个递推公式,因为买卖是两个公式。这道题与上一道不同的是,这道题我们需要列一个什么都不做的操作,来使递推公式能够模拟第一次买入的时候也可以像其他时候买入那样具有泛型的规律。这样说起来可能太抽象了,在后面读者可以自行感悟。
dp数组含义:二维部分是需要2*k+1个这么大的空间。且含义与之前相同。
递推公式:由于我们是借助循环来模拟列出各个递推公式,而每一次买卖需要两个递推公式,那么很显然我们只需列出两个递推公式让它们循环k次就可以了。
两个递推公式分别是:
dp[i][j+1]=max(dp[i-1][j+1],dp[i-1][j]-prices[i]);
dp[i][j+2]=max(dp[i-1][j+2],dp[i-1][j+1]+prices[i]);
对上面两个递推公式做一个简单的解释,为什么是j+1,和j+2,而j又是什么呢?j其实是用来模拟第几次买卖的变量,j从0开始走,我们已经说过了,前面空出来一位不做操作,所以j+1模拟第一次买入,j+2模拟第一次卖出,这样就使得第一次买股票也有规律可循,dp【i】【0】实际上就是为了占位的,它被初始化为0。方便了第一次的买入。j每次向后走两位。
初始化:初始化和上面的一样,也是买入初始化为-prices【i】,卖出初始化为0。只不过我们这里在创建数组时候,将各个位置初始为0之后,应该再用for循环把买入股票再初始化一次。关于这里为什么总要把买股票初始化为-prices【i】,不懂得也可以去看上一期文章,买股票最开始假设的是起初拥有现金0元,如果不初始化一下的话,就会导致一直为0,不买入股票。
class Solution {
public:int maxProfit(int k, vector<int>& prices) {vector<vector<int>>dp(prices.size(),vector<int>(2*k+1,0));for(int j=1;j<2*k;j+=2)dp[0][j]=-prices[0];for(int i=1;i<prices.size();i++){for(int j=0;j<2*k;j+=2){dp[i][j+1]=max(dp[i-1][j+1],dp[i-1][j]-prices[i]);dp[i][j+2]=max(dp[i-1][j+2],dp[i-1][j+1]+prices[i]);}}return dp[prices.size()-1][2*k];}
};
以上就是本文章的全部内容,两道题都是困难难度的题,但是明白的思路会发现其实并没有那么难。
总结:
今天我们完成了买卖股票的最佳时机 III、买卖股票的最佳时机 IV两道题,相关的思想需要多复习回顾。接下来,我们继续进行算法练习。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【算法练习Day42】买卖股票的最佳时机 III买卖股票的最佳时机 IV
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 买卖股票的最佳时机 III买卖…...
苹果手机如何备份通讯录?看完这篇就懂了!
如果遇到手机丢失或者出现故障的情况,通讯录备份可以避免联系人信息丢失。另外,当用户更换手机或者进行数据迁移时,提前备份好的通讯录数据可以快速还原到新设备上,避免了手动输入联系人的麻烦。苹果手机如何备份通讯录࿱…...

[yarn]yarn异常
一、运行一下算圆周率的测试代码,看下报错 cd /home/data_warehouse/module/hadoop-3.1.3/share/hadoop/mapreduce hadoop jar hadoop-mapreduce-examples-3.1.3.jar pi 1000 1000 后面2个数字参数的含义: 第1个1000指的是要运行1000次map任务 …...

C++ NULL 与nullptr 区别
在编写C程序的时候只看到过NULL,而在C的编程中,我们可以看到NULL和nullptr两种关键字,其实nullptr是C11版本中新加入的,它的出现是为了解决NULL表示空指针在C中具有二义性的问题。 一、C程序中的NULL 在C语言中,NULL…...
Google Chrome 浏览器 119.0.6045.106 版本提示 STATUS_INVALID_IMAGE_HASH 崩溃
问题 今天更新 Google Chrome 浏览器到 119.0.6045.106 版本,然后访问页面不是空白,就是页面崩溃了 解决方案 我在网上找了几种,下面这个方式符合,能解决我的问题,就是在快捷方式的属性那里,找到目标给它…...

网络IO
网络IO 阻塞模型 在之前网络通信都是阻塞模型 客户端向服务端发出请求后,客户端会一直处于等待状态,直到服务器端返回结果或网络出现问题 服务器端也是如此,在处理某个客户端A发来的请求时,另一个客户端B发来的请求会等待…...
)
数据库管理-第115期 too many open files(202301107)
数据库管理-第115期 too many open files(202301107) 这是我上周末帮朋友站台过程中处理的一个问题。 1 背景 其实这是别人搭的一个使用CentOS 7.8系统安装的一套11.2.0.4(无补丁)的双节点RAC,用于迁移以前运行在So…...

一行命令让你的服务器命令行亮起来!!!!
if [ "$(whoami)" "root" ]; then echo "PS1${debian_chroot:($debian_chroot)}\[\033[01;32m\]\u\h\[\033[00m\]:\[\033[01;34m\]\w\[\033[00m\]# " >> /root/.bashrc; source /root/.bashrc; echo "已为root用户设置提示符以#结尾…...

线性代数(二)| 行列式性质 求值 特殊行列式 加边法 归纳法等多种方法
文章目录 1. 性质1.1 重要性质梳理1.1.1 转置和初等变换1.1.2加法行列式可拆分1.1.3 乘积行列式可拆分 1.2 行列式性质的应用1.2.1 简化运算1.2.2 将行列式转换为(二)中的特殊行列式 2 特殊行列式2.1 上三角或下三角行列式2.2 三叉行列式2.3 行列式行和&…...

OpenCV入门7:图像形态学变换
形态学是一种针对图像形状和结构进行操作和分析的图像处理方法。在OpenCV中,提供了一些函数和方法用于执行形态学操作。下面将介绍一些常见的形态学操作及其在OpenCV中的实现方式。 膨胀(Dilation): 膨胀操作可以扩展图像中的边…...

Apache Storm 2.5.0 集群安装与配置
1、下载Apache Storm 2.5.0 https://mirrors.tuna.tsinghua.edu.cn/apache/storm/apache-storm-2.5.0/ 2、准备3台服务器 192.168.42.139 node1 192.168.42.140 node1 192.168.42.141 node2 3、配置host [rootnode1 ~]# cat /etc/hosts 127.0.0.1 localhost localhost…...

Android-将编码的base64图像,添加水印,转换成File存储到手机
一、将图片file转换成bitmap Bitmap bitmap = BitmapFactory.decodeFile(file.getAbsolutePath()); 二、给图片添加水印 String[] content = new String[]{"纬度:" + latitude, "经度:" + longitude, "地址:" + signAddress, "时间:&…...
AI 绘画 | Stable Diffusion 图生图
图生图简介 Stable Diffusion 不仅可以文生图,还可以图生图。文生图就是完全用提示词文本去生成我们想要图片,但是很多时候会有词不达意的感觉。就像我们房子装修一样,我们只是通过文字描述很难表达出准确的想要的装修效果,如果能…...
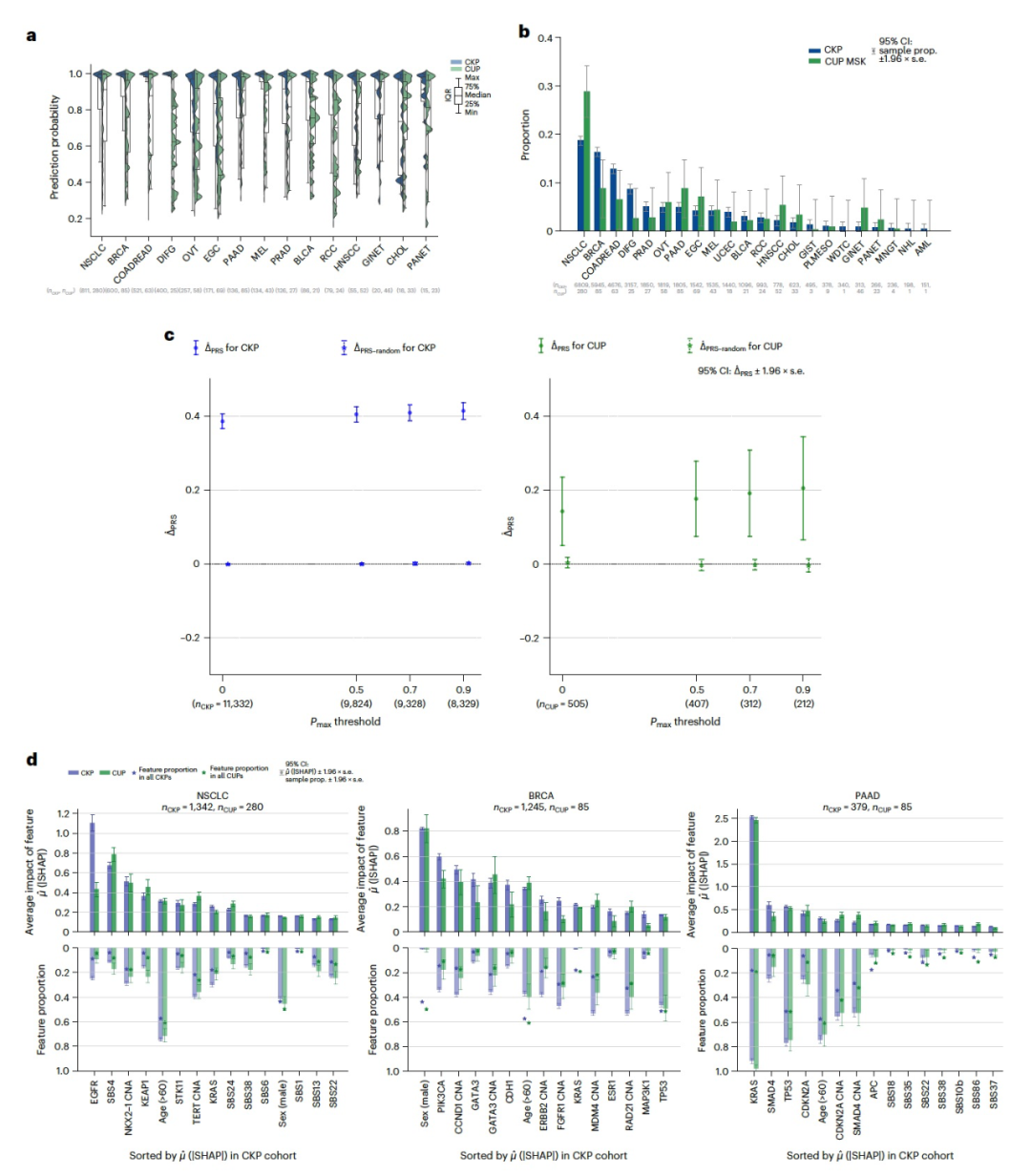
Nat. Med. | 基于遗传学原发部位未知癌症的分类和治疗反应预测
今天为大家介绍的是来自Alexander Gusev团队的一篇论文。原发部位未知癌症(Cancer of unknown primary,CUP)是一种无法追溯到其原发部位的癌症,占所有癌症的3-5%。CUP缺乏已建立的靶向治疗方法,导致普遍预后…...

RocketMQ如何安全的批量发送消息❓
优点: 批量发送消息可以提高rocketmq的生产者性能和吞吐量。 使用场景: 发送大量小型消息时;需要降低消息发送延迟时;需要提高生产者性能时; 注意事项: 消息列表的大小不能超过broker设置的最大消息大小;消息列表…...

计算机视觉与深度学习 | 基于视觉惯性紧耦合的SLAM后端优化算法
===================================================== github:https://github.com/MichaelBeechan CSDN:https://blog.csdn.net/u011344545 ===================================================== 基于视觉惯性紧耦合的SLAM后端优化算法 引言视觉惯性联合初始化非线性优…...

GDI+ 绘制透明图
目录 一、GDI+ 准备工作 1、线程中添加GDI+支持 2、Gdiplus::Bitmap 1)、从文件创建位图...

【Java】IntelliJ IDEA使用JDBC连接MySQL数据库并写入数据
目录 0 准备工作1 创建Java项目2 添加JDBC 驱动程序3 创建数据库连接配置文件4 创建一个 Java 类来连接和操作数据库5 运行应用程序 在 IntelliJ IDEA 中连接 MySQL 数据库并将数据存储在数据表中,使用 Java 和 JDBC(Java Database Connectivity…...

Linux Hadoop平台伪分布式安装
Linux Hadoop 伪分布式安装 1. JDK2. Hadoop3. MysqlHive3.1 Mysql8安装3.2 Hive安装 4. Spark4.1 Maven安装4.2 Scala安装4.3 Spark编译并安装 5. Zookeeper6. HBase 版本概要: jdk: jdk-8u391-linux-x64.tar.gzhadoop:hadoop-3.3.1.tar.gzh…...
【STM32-DSP库的使用】基于Keil5 + STM32CubeMX 手动添加、库添加方式
STM32-DSP库的使用 一.CMSIS-DSP1.1 DSP库简介1.2 支持的函数类别1.3 宏定义 二、操作2.1 STM32CubeMX 配置基本工程2.2 Lib库的方式实现(推荐)2.3 手动添加DSP文件(可以下载官方最新库,功能齐全) 三、MFCC测试DSP加速效果 为验证语音识别MFC…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
