Python曲线肘部点检测-膝部点自动检测
文章目录
- 一. 术语解释
- 二. 拐点检测
肘部法则是经常使用的法则。很多时候,可以凭人工经验去找最优拐点,但有时需要自动寻找拐点。最近解决了一下这个问题,希望对各位有用。
一. 术语解释
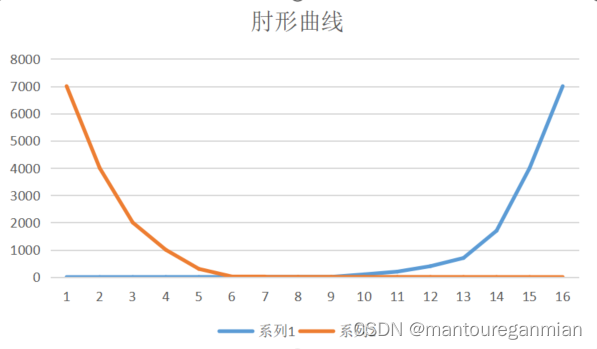
**肘形曲线(elbow curve)**类似人胳膊状的曲线,拐点在肘部。**膝形曲线(knee curve)人腿形的曲线,拐点在膝盖。这类曲线和二八原则(即帕托累法则)**不谋而合,做决策时,自然选择肘点或膝点做参考。按照拐点在左还是右侧来分,细分为:左膝点曲线,右膝点曲线,左肘点曲线,右肘点曲线。
曲线示意图如下:
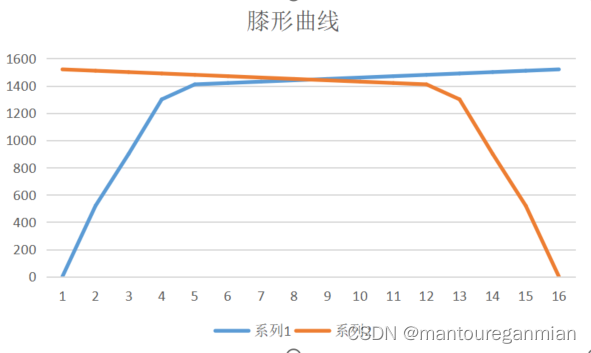
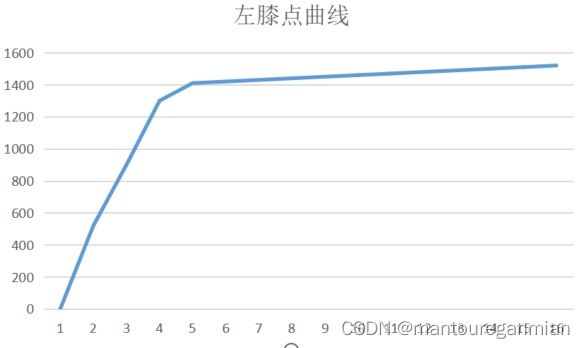
左膝点曲线膝点在左边的曲线(术语是我自己起的,明白意思就好,膝点在左边)如下:
从形状上,四种曲线没有大的区别,可以相互转化:
- 肘曲线与膝曲线相互转化,用曲线最大值减去曲线各点值即可。
- 同类型曲线,左右拐点转化,就是切换升序降序排序即可。
它们都可以计算拐点,其中以左膝点曲线(见下图)计算拐点最简单,所以以其为标准曲线。
二. 拐点检测
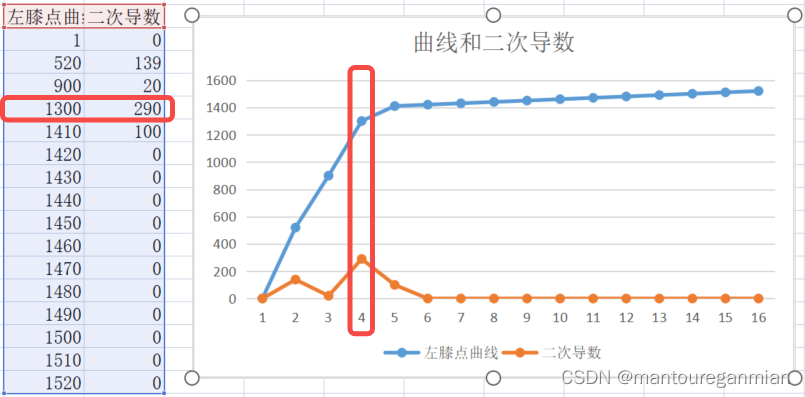
左膝点曲线,原理是其二次曲线导数最大点,如下:
对于离散序列来说,当x轴差为1时,二次曲线计算公式为:
f′′(xi)=f(xi−1)+f(xi+1)−2∗f(xi)f''(x_i) = f(x_{i-1}) +f(x_{i+1}) - 2*f(x_i)f′′(xi)=f(xi−1)+f(xi+1)−2∗f(xi)
推荐一个简单的包:kneed Github地址
支持:Python 3.7, 3.8, 3.9, and 3.10. 安装如下:
$ conda install -c conda-forge kneed
# 或者
$ pip install kneed # To install only knee-detection algorithm
$ pip install kneed[plot] # To also install plotting functions for quick
使用如下:
from kneed import DataGenerator, KneeLocatorx, y = DataGenerator.figure2()print([round(i, 3) for i in x])
print([round(i, 3) for i in y])# out: [0.0, 0.111, 0.222, 0.333, 0.444, 0.556, 0.667, 0.778, 0.889, 1.0]
# out: [-5.0, 0.263, 1.897, 2.692, 3.163, 3.475, 3.696, 3.861, 3.989, 4.091]kneedle = KneeLocator(x, y, S=1.0, curve="concave", direction="increasing")print(round(kneedle.knee, 3))
# out: 0.222print(round(kneedle.elbow, 3))
# out: 0.222
相关文章:

Python曲线肘部点检测-膝部点自动检测
文章目录一. 术语解释二. 拐点检测肘部法则是经常使用的法则。很多时候,可以凭人工经验去找最优拐点,但有时需要自动寻找拐点。最近解决了一下这个问题,希望对各位有用。一. 术语解释 **肘形曲线(elbow curve)**类似人胳膊状的曲线ÿ…...
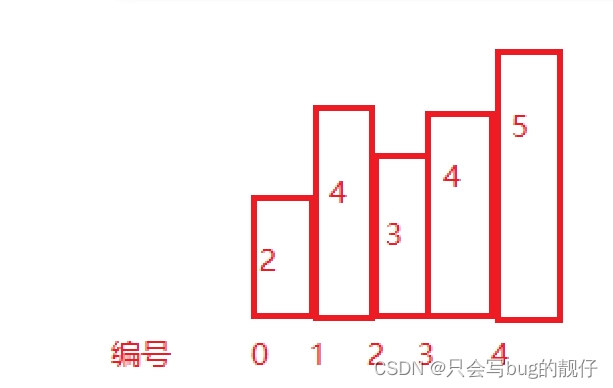
【算法题】最大矩形面积,单调栈解法
力扣:84. 柱状图中最大的矩形 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。 题意很简单,翻译一下就是:求该图中…...

活动策划|深度分析年货节活动该如何策划!
四月初,不平凡的初春开始恢复往日的平静。对于新零售行业,疫情的缓解也逐渐平稳生态链的运转。2020年新零售的格局在洗礼后,业务的聚焦点也从前端促销转移到后端履约的体验闭环,同时很大程度的推进企业在危机公关下的应对。618大促…...

Idea启动遇到 Web server failed to start. Port 8080 was already in use. 报错
Idea启动遇到问题-记录 报错英文提示: APPLICATION FAILED TO START Description: Web server failed to start. Port 8080 was already in use. Action: Identify and stop the process that’s listening on port 8080 or configure this application to liste…...
函数知识点总结)
Python3中zip()函数知识点总结
1.引言 在本文中,我将带领大家深入了解Python中的zip()函数,使用它可以提升大家的工作效率。 闲话少说,我们直接开始吧! 2. 基础知识 首先,我们来介绍一些基础知识点: Python中的某些数据类型是不可变的…...

过滤器,监听器,拦截器的原理与在Servlet和Spring的应用
在Java Web的开发中,最原始和初期的学习都是从Servlet开始的,Servlet是Java最为耀眼的技术,也是Java EE的技术变革。目前大火主流的框架spring boot也的spring mvc部分也是基于拓展servlet完成的。回到之前的文章spring 实现了对servlet的封装…...

minio spring boot 秒传、分片上传、断点续传文件实现
此处后端使用的是前期封装的自定义starter,具体链接可参考:minio对象存储spring boot starter封装组件 这里主要针对前期封装的组件,做一个简单的应用,前端直传可查看之前的文章 秒传 秒传的逻辑比较简单,在前传上传…...

MTK平台使用Omnipeek分析空口协议讲解
讲解这个之前,我们先来了解下beacon/robe Request/Probe Response 三种帧 beacon帧 信标帧,由AP以一定的时间间隔周期性发出,以此来告诉外界自己无线网络的存在。 Beacon帧作为802.11中一个周期性的帧,Beacon周期调高,对应睡眠周期拉长,故节能(即越来休息100ms再起来…...
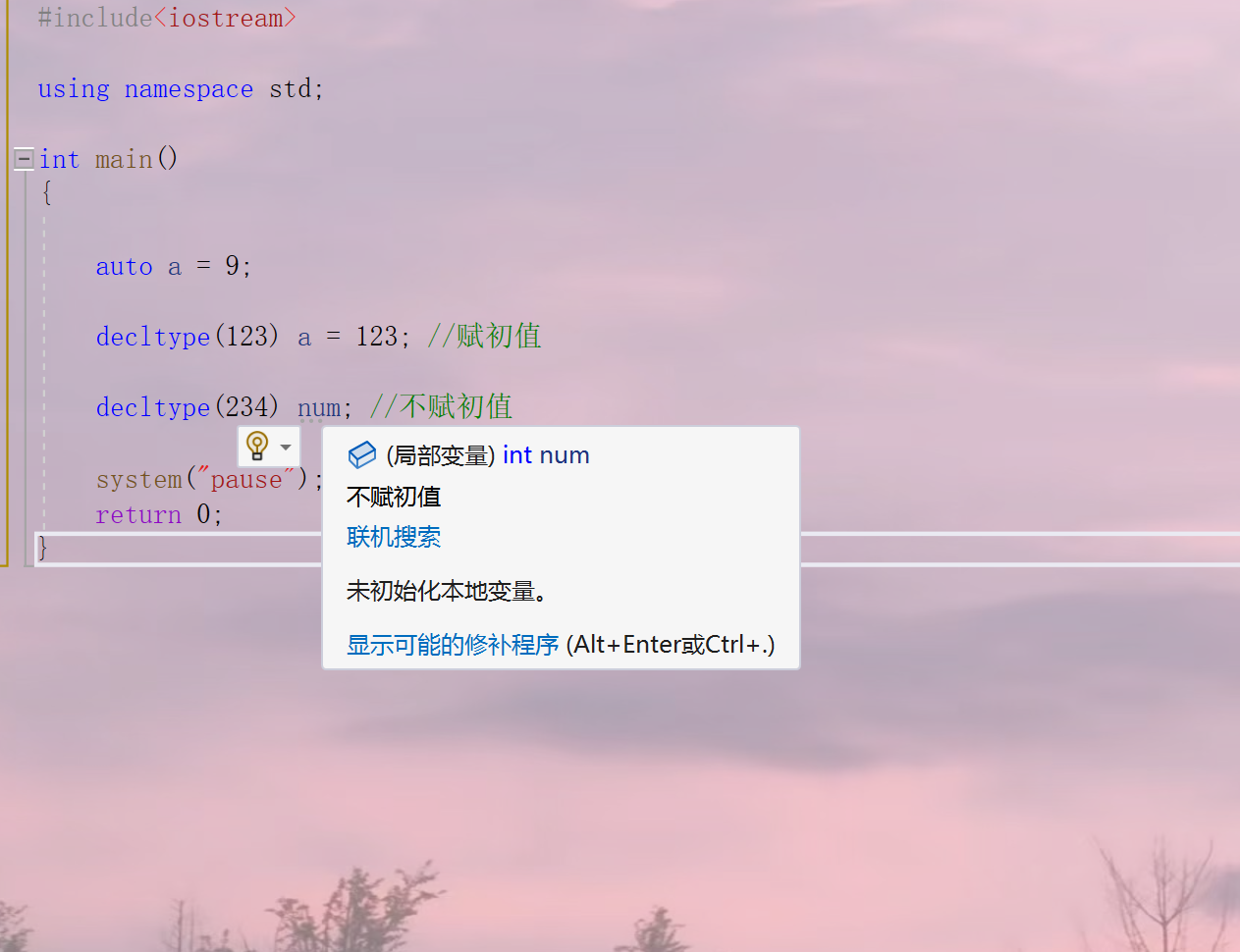
string和自动推断类型
欢迎来观看温柔了岁月.c的博客目前设有C学习专栏C语言项目专栏数据结构与算法专栏目前主要更新C学习专栏,C语言项目专栏不定时更新待C专栏完毕,会陆续更新C项目专栏和数据结构与算法专栏一周主要三更,星期三,星期五,星…...
【软件测试】从功能到自动化测试,测试人的进阶之路细节,这些必不可少......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 测试流程࿰…...
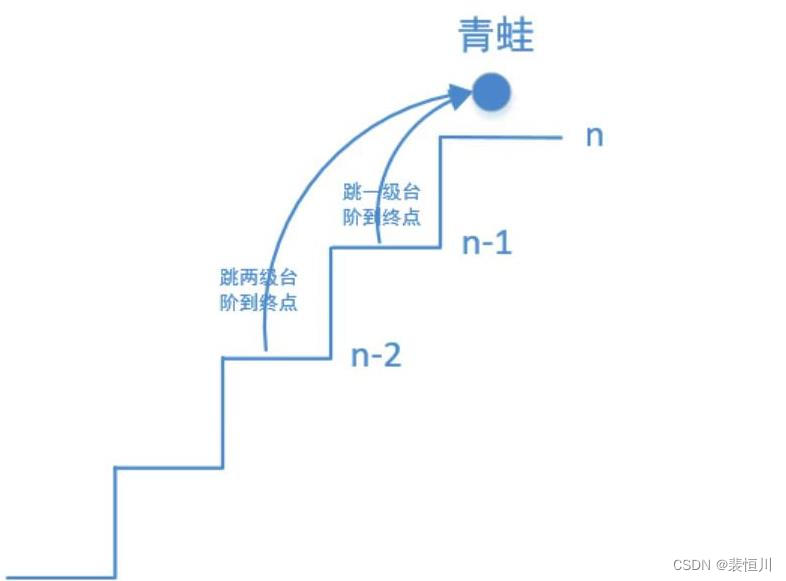
C语言青蛙跳台阶【图文详解】
青蛙跳台阶前言1. 题目介绍2. 解题思路3. 利用图片来演示青蛙跳台阶的原理4. 如何用C语言实现青蛙跳台阶前言 在本文,我们要与一只活泼可爱的小青蛙合作,带领着它跳上台阶,这个小家伙精力充沛,特别擅长于跳跃。我们要让它做我们的…...
——list容器的基础理论知识)
笔记(五)——list容器的基础理论知识
list容器是一个双向链表容器,可以高效地进行插入删除元素,但是不能随机存取元素(不支持at()和[]操作符)。一、list容器的对象构造方法list对象采用模板类的默认构造形式例如list<T> lst;#include<iostream>…...

浅谈网络中接口幂等性设计问题
所谓幂等性设计,就是说,一次和多次请求某一个资源应该具有同样的副作用。用数学的语言来表达就是:f(x) f(f(x))。 在数学里,幂等有两种主要的定义。 在某二元运算下,幂等元素是指被自己重复运算(或对于函数…...
《C Primer Plus》第13章复习题与编程练习
《C Primer Plus》第13章复习题与编程练习复习题1. 下面的程序有什么问题?2. 下面的程序完成什么任务?(假设在命令行环境中运行)3. 假设程序中有下列语句:4. 编写一个程序,不接受任何命令行参数或接受一个命…...

计算机SCI论文应该怎么作图? - 易智编译EaseEditing
计算机SCI论文,作图时要注意以下几个方面的问题: 1.图片的格式要tiff或者eps; 2.文件大小不能超过10M; 3.长和宽也给出了具体要求; 4.色彩模式要RGB或者灰度图; 5.文中的文字字体和大小; …...
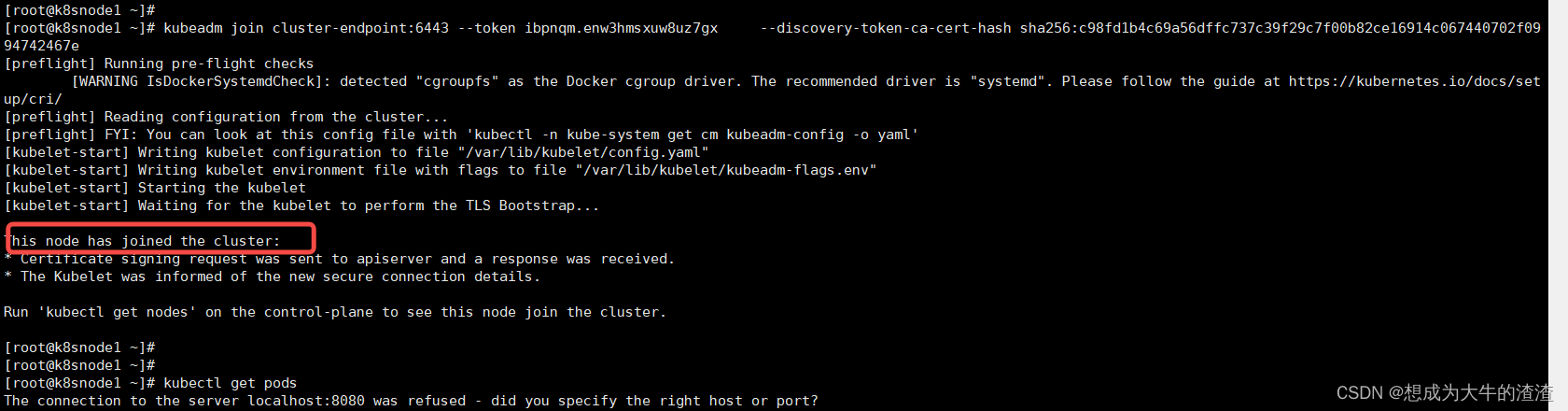
【一】kubernetes集群部署
一、docker环境搭建 1、移除以前docker相关包 sudo yum remove docker docker-client docker-client-latest docker-common docker-latest docker-latest-logrotate docker-logrotate docker-engine2、配置yam源 sudo yum install -y yum-utilssudo yum-config-manager --ad…...

Docker安装Redis
一、拉取镜像 命令::docker pull <镜像名称>:<版本号> docker pull redis 二:Docker挂载配置文件 挂载:即将宿主的文件和容器内部目录相关联,相互绑定,在宿主机内修改文件的话也随之修改容…...
 系统执行的过程)
在shell中执行一条可执行程序(./a.out) 系统执行的过程
目录 系统调度过程 用户空间角度: 内核角度 1、调用fork创建一个新进程 2、使用_fo_fork创建新进程 3、父进程调用wake_up_new_task尝试唤醒新进程 4、CPU选择一个合适的进程来运行; 5、运行新进程 6、实现负载均衡 系统调度过程 分析在命令行…...
【ArcGIS Pro二次开发】(10):属性表字段(field)的修改
在ArcGIS Pro中,经常会遇到用字段计算器对要素的属性表进行计算。下面以一个例子演示如何在ArcGIS Pro SDK二次开发中实现。 一、要实现的功能 如上图所示的要素图层,要实现如下功能: 当字段【市级行政区】的值为【泉州市】时,将…...

数据结构与算法—散列表
目录 散列表 散列函数 散列冲突解决 1、开放寻址法 1.1 线性探测 1.2 二次探测 1.3 双重散列 2、链表法 使用场景 单词查找 散列表与链表的结合使用LRU 散列表总结 散列表实例 散列表 Word 单词拼写功能,如何实现的?散列表(Has…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
