希尔排序原理
目录:
一、希尔排序与插入排序
1)希尔排序的概念
2)插入排序实现
二、希尔排序实现
一、希尔排序与插入排序
1)希尔排序的概念
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止。
2)插入排序实现
既然希尔排序是插入排序的优化,那么我们有必要先了解一下插入排序的过程,基本操作是将需要进行排序的元素插入到已排序区当中,这样每次插入都会使已排序区长度加一。
直观的看,插入排序的操作就和我们在打扑克牌时一样,我们默认将小的或者大的往一边插进去,插入排序也是如此。
1、我们从第二个元素开始插入排序,因为这样左边只有一个数,必然有序,我们把左边的称为已排序区,右边的称为待排序区。
2、将待排序区的第一个元素向已排序区插入,将其与已排序区元素从后向前比较,将其插入到合适位置,已排序区元素个数+1。
3、然后待排序区重复2的步骤向已排序区从后往前比较,找到合适位置插入。
4、 继续将待排序区元素插入到已排序区,当待排序区元素为0时,这组数据就已经排序完成。
我们明白了插入排序的过程,接下来就是实现插入排序了,我们先来分析,插入排序中第一个元素(0位置处)本来就是有序的,所以我们直接从第二个元素开始操作(1位置处)。
1、定义待排序区的首元素下标为end,用tmp记录下end下标的元素,将tmp与已排序区元素进行比较,发现小于5,则将待排序区的元素插入到首元素位置。
2、已排序区数组元素加一,待排序区首元素变为3,end也变为3的下标,tmp记录此元素的值,将tmp与已排序区元素进行比较,首先与5比较,小于5。
3、再跟1比较发现大于1,那么这个值就插入在1和5之间,已排序元素加一,待排序数组元素减一。
4、一直刷新end与tmp值,与已排序区进行从右往左的比较,比较到合适的位置才进行插入,而不是每次比较都插入元素。
时间复杂度:最坏情况下为 O(N^2),此时待排序列为逆序,或者说接近逆序。最好情况下为 O(N),此时待排序列为升序,或者说接近升序。平均为O(N^2)。
空间复杂度:没有额外使用空间,所以空间复杂度为 O(1)。
代码实现:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>void InsertSort(int *a, int len)//插入排序
{int i = 0;for(i = 1 ; i < len ; i++)//从下标为1的位置进行插入排序{int end = i;//用end记录待排序区的首元素下标int tmp = a[end];//用tmp记录待排序区首元素的值while(end > 0)//保证不越界tmp就一直往前进行比较,找到合适的位置break{if(a[end - 1] > tmp){a[end] = a[end - 1];end--;}else{break;}}a[end] = tmp;//最后在将tmp值放在end的下标下}
}void Print(int *a, int len)//打印数组元素
{int i = 0;for(i = 0 ; i < len ; i++){printf("%3d",a[i]);}printf("\n");return;
}void Test()//测试
{int a[] = { 9, 8, 7, 6, 5, 4, 3, 2, 1 };int len = sizeof(a) / sizeof(int);InsertSort(a, len);Print(a, len);return;
}int main()
{Test(); return 0;
}运行结果:
二、希尔排序实现
希尔排序法又称为缩小增量法。希尔排序法的基本思想是:首先选定一个整数,把待排序文件中所有记录分成gap个组(增量),所有距离为gap的数据记录在同一组内,并对每一组内的记录进行排序。然后,再取gap/2个组(缩小增量),重复上述分组和排序的工作。当gap == 1时所有记录在统一组内排好序。
注:希尔排序缩小增量在数学上是个难题,大家经常用的就是gap/2。
我们有这样一个数组:a[] = {6, 1, 5, 2, 4, 8, 3, 7, 9}。我们对这个数组进行排序,首先假设设置gap的值为3,那么这组数就会分为三组:

接下来控制这三组,每组分别进行插入排序,结果为:

那么gap为3时的所有组已经排完了,接下来就该缩小增量了,gap /= 2,gap == 1:

知晓了希尔排序是如何进行数据管理的,下面来看看具体的操作是如何完成的:
1、首先, 我们需要对gap进行控制,在gap>0范围内,每次分组后的所有组排完序之后都要除以二,可以用while循环来控制gap的大小:
void ShellSort(int *a, int n)
{assert(a);int gap = n;int i = 0;while(gap > 1){if(gap > 1)gap /= 2;//..分完组后的预排序 }
}2、我们已经将缩小增量设置好了,接下来只需要把每次分完组都进行排序,也就是预排序。如何进行预排序呢?既然希尔排序是插入排序的优化,我们不妨以插排的思路对希尔预排序进行调整。
用for循环对所有数据进行预排序,值得注意的是这里不会像插排那样循环到n,我们只需要限制在n - gap 的范围就行了,例如上图:

这个数组从3往后就不需要排了,因为在每一组的排序中最后一个值都是被拍过序的,没必要再次进行一次排序,总共为n个数据,那么就是只需要n - gap - 1个数据进行排序。则:
void ShellSort(int *a, int n)
{assert(a);int gap = n;int i = 0;while(gap > 1){if(gap > 1)gap /= 2;for(i = 0 ; i < n - gap ; i++)//控制n - gap数据进行预排序{//具体排序过程...}}
}3、其实预排序的实现和直接插入排序的过程几乎是完全相似,前面也说了当希尔排序的缩小增量为1时,和插入排序没区别,也就是说,插入排序每次都对相邻的数据处理,而希尔排序是将分好的组看成新的数组,例如上面数据的6, 2, 3为一组,我们可以看成其他的数据不存在,只有这一组存在,那么对于这一组而言,希尔排序就是插入排序,将上图的三组都排完序,这一趟预排序就算完成了。
与插入排序相同,定义一个end记录当前元素下标,定义一个tmp记录a[end + gap]处的值,为什么不是a[end]处的值?可别忘了第一个值是默认有序的,所以要从第二个值向前比较,当end对应的值要大于tmp那么就将end处的值赋给下一个位置,也就是end+gap处,当不满足end处的值大于end+gap时,代表前面已经没有比自己大的值了,直接break,最后在循环结束的时候记得将a[end + gap]之前被覆盖的地方重新赋值:
void ShellSort(int *a, int n)
{assert(a);int gap = n;int i = 0;while(gap > 1){if(gap > 1)gap /= 2;for( i = 0; i < n - gap; i++)//对n组数据进行n - gap次预排序{int end = i;int tmp = a[gap + end];while(end >= 0)//当end >= 0时候对每组进行预排序{if(tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}return;
}这样希尔排序就完成了,其实在希尔排序的过程中,或许你还有疑问,为什么for循环这里是连续的?不是进行分组了吗?其实你仔细想想, 我们还是以上面gap==3为例,首先是第一个数据,就是对第一组的首个数据进行排序,当到了第二个数据的时候,就是对第二组首个数据进行排序,但是因为有gap的控制,这两组数据其实是互不影响的,所以连续的遍历数据进行预排序也是没有问题的。
总结希尔排序的特性:
1、希尔排序是对直接插入排序的优化。
2、当gap > 1时,都是预排序,目的是让数组更接近有序,当gap==1时,将前面预排序的结果进行直接插入排序而完成排序。
时间复杂度:O(NlogN)(近似),因为增量问题并不能准确得出时间复杂度。
空间复杂度:没有开额外的空间,所以空间复杂度为O(1)。
以下是希尔排序的完整代码:
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>void ShellSort(int *a, int n)
{assert(a);int gap = n;int i = 0;while(gap > 1){if(gap > 1)gap /= 2;for( i = 0; i < n - gap; i++)//对n组数据进行n - gap次预排序{int end = i;int tmp = a[gap + end];while(end >= 0)//当end >= 0时候对每组进行预排序{if(tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}return;
}void Print(int *a, int n)
{assert(a);int i = 0;for(i = 0 ; i < n ; i++){printf("%d ",a[i]); }printf("\n");return;
}int main()
{int a[] = {5,6,1,2,7,4,8,3,9};int len = sizeof(a) / sizeof(int);ShellSort(a, len);Print(a, len);return 0;
}

如果这篇文章对你有帮助的话,还望各位佬能多多三连~~[doge][玫瑰]
相关文章:

希尔排序原理
目录: 一、希尔排序与插入排序 1)希尔排序的概念 2)插入排序实现 二、希尔排序实现 一、希尔排序与插入排序 1)希尔排序的概念 希尔排序(Shells Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Incremen…...
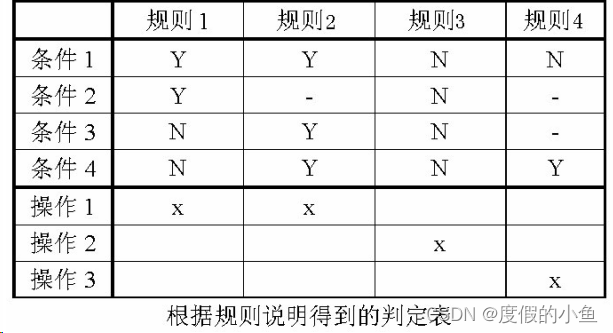
测试用例的设计方法(全):判定表驱动分析方法
目录 判定表驱动分析方法 一. 方法简介 二. 实战演习 判定表驱动分析方法 一. 方法简介 1.定义:判定表是分析和表达多逻辑条件下执行不同操作的情况的工具。 2.判定表的优点 能够将复杂的问题按照各种可能的情况全部列举出来,简明并避免遗漏。因此…...
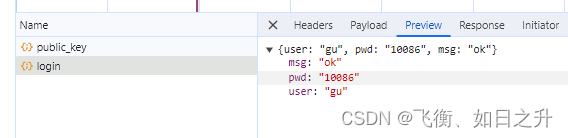
node 第十七天 使用rsa非对称加密 实现前后端加密通信 JSEncrypt和node-rsa
什么是非对称加密 加密过程需要两个钥匙, 公钥和私钥 其中公钥用于加密明文, 私钥用于解密公钥加密的密文, 解密只可以用私钥 公钥和私钥是一对一的关系 公钥可以发送给用户, 不用担心泄露 私钥需要保存在服务端, 不能泄露 例如: 战场上,B要给A传递一条消息…...

Spring-依赖注入findAutowireCandidates源码实现
findAutowireCandidates()实现 1、找出BeanFactory中类型为type的所有的Bean的名字,根据BeanDefinition就能判断和当前type是不是匹配,不用生成Bean对象 2、把resolvableDependencies中key为type的对象找出来并添加到result中 3、遍历根据type找出的b…...

单页面应用与多页面应用的区别?
单页面应用(SPA)与多页面应用(MPA)的主要区别在于页面数量和页面跳转方式。单页面应用只有一个主页,而多页面应用包含多个页面。 单页面应用的优点有: 用户体验好:内容的改变不需要重新加载整…...

模型预处理的ToTensor和Normalize
模型预处理的ToTensor和Normalize flyfish import torch import numpy as np from torchvision import transformsmean (0.485, 0.456, 0.406) std (0.229, 0.224, 0.225)# data0 np.random.randint(0,255,size [4,5,3],dtypeuint8) # data0 data0.astype(np.float64) da…...

nodejs express multer 保存文件名为中文时乱码,问题解决 originalname
nodejs express multer 保存文件名为中文时乱码,问题解决 originalname 一、问题描述 用 express 写了个后台,在接收文件并保存的时候 multer 接收到的文件名为乱码。 二、解决 找了下解决方法,在 github 的 multer issue 中找到了答案 参…...
)
大数据之LibrA数据库系统告警处理(ALM-12035 恢复任务失败后数据状态未知)
告警解释 执行恢复任务失败后,系统会自动回滚,如果回滚失败,可能会导致数据丢失等问题,如果该情况出现,则上报告警,如果下一次该任务恢复成功,则恢复告警。 告警属性 告警ID 告警级别 可自动…...
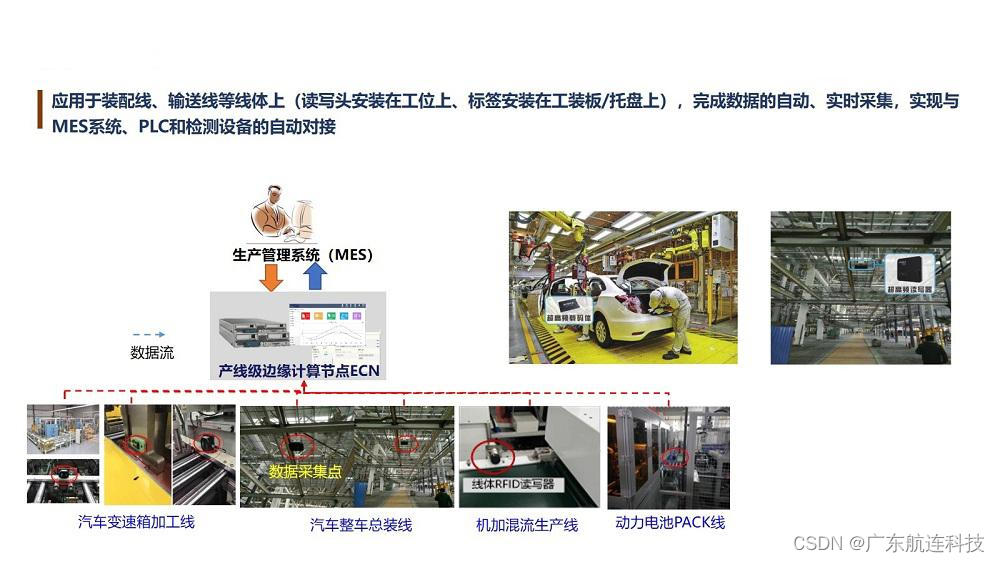
汽车生产RFID智能制造设计解决方案与思路
汽车行业需求 汽车行业正面临着快速变革,传统的汽车制造方式正在向柔性化、数字化、自动化和数据化的智能制造体系转变,在这个变革的背景下,汽车制造企业面临着物流、生产、配送和资产管理等方面的挑战,为了应对这些挑战…...

讲解机器学习中的 K-均值聚类算法及其优缺点。
K-均值聚类算法是一种无监督学习算法,常用于对数据进行聚类分析。其主要步骤如下: 首先随机选择K个中心点(质心)作为初始聚类中心。 对于每一个样本,计算其与每一个中心点的距离,将其归到距离最近的中心点…...
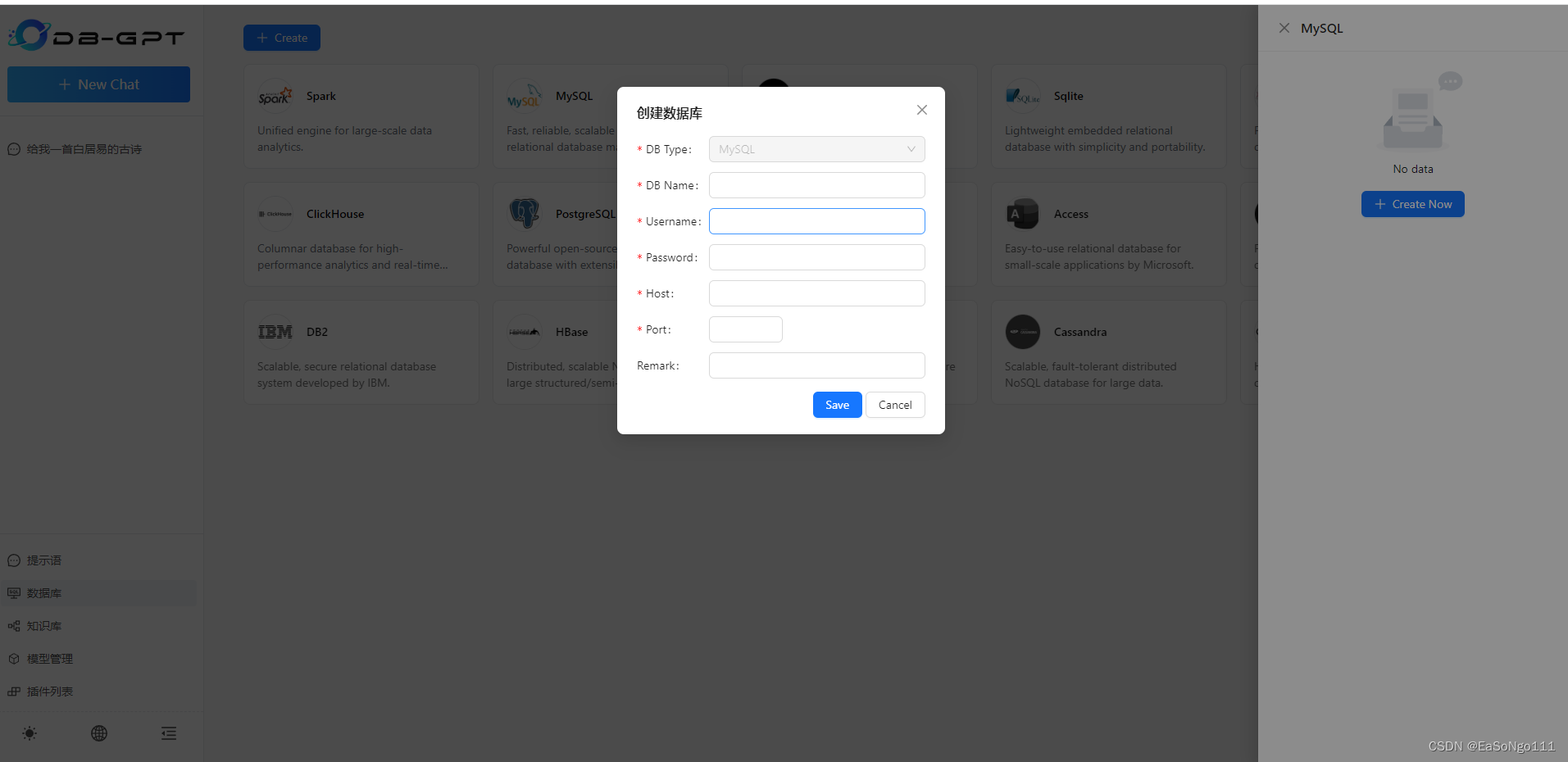
开源DB-GPT实现连接数据库详细步骤
官方文档:欢迎来到DB-GPT中文文档 — DB-GPT 👏👏 0.4.1 第一步:安装Minicoda https://docs.conda.io/en/latest/miniconda.html 第二步:安装Git Git - Downloading Package 第三步:安装embedding 模型到…...

java学习part01
15-Java语言概述-单行注释和多行注释的使用_哔哩哔哩_bilibili 1.命令行 javac编译出class文件 然后java运行 2. java文件每个文件最多一个public类 3.java注释 单行注释 // 多行注释 文档注释 文档注释内容可以被JDK提供的工具javadoc所解析,生成一套以网页文…...
渗透测试学习day3
文章目录 靶机:DancingTask 1Task 2Task 3Task 4Task 5Task 6Task 7Task 8 靶机:RedeemerTask 1Task 2Task 3Task 4Task 5Task 6Task 7Task 8Task 9Task 10Task 11 靶机:AppointmentTask 1Task 2Task 3Task 4Task 5Task 6Task 7Task 8Task 9T…...

【Proteus仿真】【Arduino单片机】数码管显示
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真Arduino单片机控制器,使用TM1637、共阳数码管等。 主要功能: 系统运行后,数码管显示数字、字符。 二、软件设计 /* 作者:嗨小易&am…...

【Bug】Python利用matplotlib绘图无法显示中文解决办法
一,问题描述 当利用matplotlib进行图形绘制时,图表标题,坐标轴,标签中文无法显示,显示为方框,并报错 运行窗口报错: 这是中文字体格式未导入的缘故。 二,解决方案 在代码import部…...
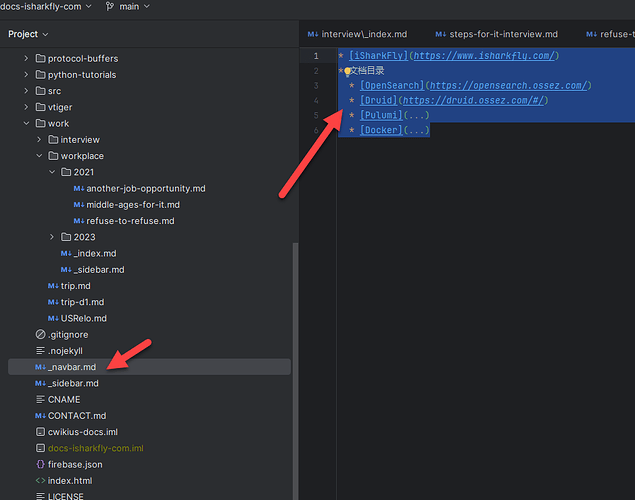
Docsify 顶部的导航是如何配置
如下图,我们在 Docsify 的文档中配置了一个顶部导航。 下面的步骤对顶部导航的配置进行简要介绍。 配置 有 2 个地方需要这个地方进行配置。 首先需要在 index.html 文件中的 loadNavbar: true, 配置上。 然后再在项目中添加一个 _navbar.md 文件。 在这个文件中…...
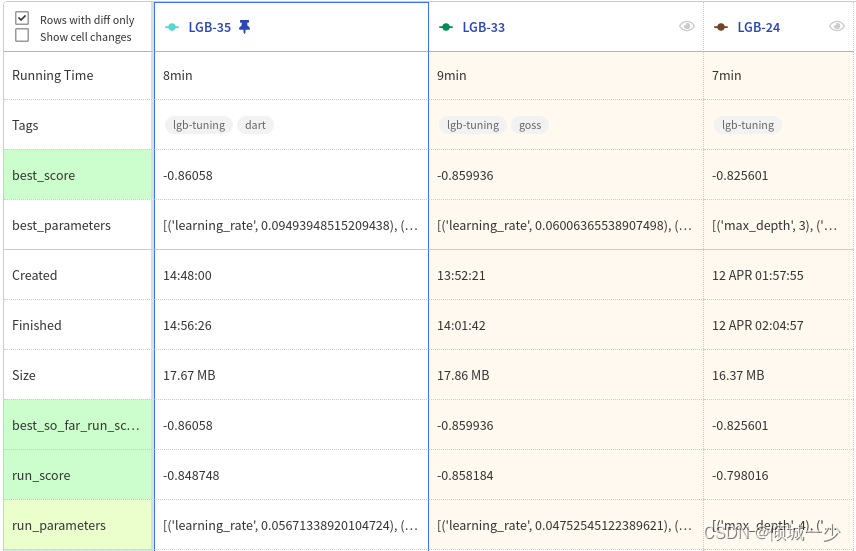
最详细的LightGBM参数介绍与深入分析
前言 我使用LightGBM有一段时间了,它一直是我处理大多数表格数据问题的首选算法。它有很多强大的功能,如果你还没有看过的话,我建议你去了解一下。 但我一直对了解哪些参数对性能影响最大,以及如何调整LightGBM参数以发挥最大作用…...

blender动画制作全流程软件
blender官网下载地址 Download — blender.org Blender是一款功能强大的免费开源的3D动画制作软件。它具有广泛的功能和工具,适用于从简单的2D动画到复杂的3D渲染和特效的各种需求。 以下是Blender的一些主要特点: 建模工具:Blender提供了一…...
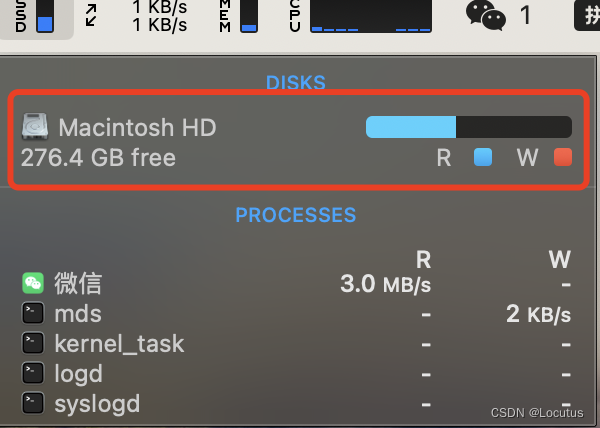
mac的可清除空间(时间机器)
看到这个可用82GB(458.3MB可清除) 顿时感觉清爽,之前的还是可用82GB(65GB可清除),安装个xcode都安装不上,费解半天,怎么都解决不了这个问题,就是买磁盘情理软件也解决不了…...

【深度学习】可交互讲解图神经网络GNN
在正式开始前,先找准图神经网络GNN(Graph Neural Network)的位置。 图神经网络GNN是深度学习的一个分支。 深度学习的四个分支对应了四种常见的数据格式,前馈神经网络FNN处理表格数据,表格数据可以是特征向量,卷积神经网络CNN处理…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

