多路查找树
1.二叉树与 B 树
1.1二叉树的问题分析
二叉树的操作效率较高,但是也存在问题, 请看下面的二叉树
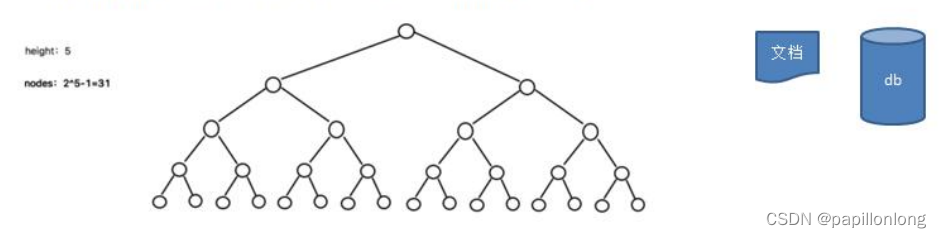
- 二叉树需要加载到内存的,如果二叉树的节点少,没有什么问题,但是如果二叉树的节点很多(比如 1 亿), 就
存在如下问题: - 问题 1:在构建二叉树时,需要多次进行 i/o 操作(海量数据存在数据库或文件中),节点海量,构建二叉树时,
速度有影响 - 问题 2:节点海量,也会造成二叉树的高度很大,会降低操作速度.
1.2多叉树
- 在二叉树中,每个节点有数据项,最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点,
就是多叉树(multiway tree) - 后面我们讲解的 2-3 树,2-3-4 树就是多叉树,多叉树通过重新组织节点,减少树的高度,能对二叉树进行优化。
- 举例说明(下面 2-3 树就是一颗多叉树
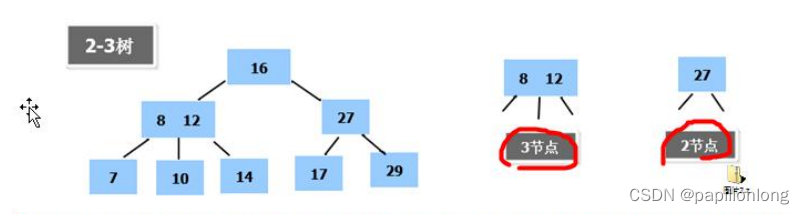
1.3B 树的基本介
B 树通过重新组织节点,降低树的高度,并且减少 i/o 读写次数来提升效率。

- 如图 B 树通过重新组织节点, 降低了树的高度.
- 文件系统及数据库系统的设计者利用了磁盘预读原理,将一个节点的大小设为等于一个页(页得大小通常为 4k),
这样每个节点只需要一次 I/O 就可以完全载入 - 将树的度 M 设置为 1024,在 600 亿个元素中最多只需要 4 次 I/O 操作就可以读取到想要的元素, B 树(B+)广泛
应用于文件存储系统以及数据库系统中
2.2-3树
2.1 2-3 树是最简单的 B 树结构, 具有如下特点
- 2-3 树的所有叶子节点都在同一层.(只要是 B 树都满足这个条件)
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点.
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点. 4) 2-3 树是由二节点和三节点构成的树
2.2 2-3 树应用案例
将数列{16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20} 构建成 2-3 树,并保证数据插入的大小顺序。(演示一下构建 2-3
树的过程.)
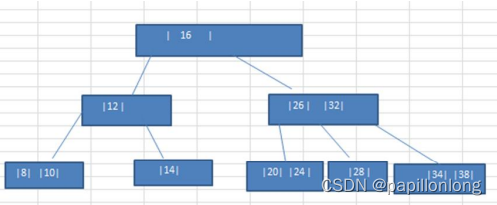
插入规则:
- 2-3 树的所有叶子节点都在同一层.(只要是 B 树都满足这个条件)
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点. 3) 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点
- 当按照规则插入一个数到某个节点时,不能满足上面三个要求,就需要拆,先向上拆,如果上层满,则拆本层,
拆后仍然需要满足上面 3 个条件。 - 对于三节点的子树的值大小仍然遵守(BST 二叉排序树)的规则
2.3 其它说明
除了 23 树,还有234 树等,概念和 23 树类似,也是一种 B 树。 如图:
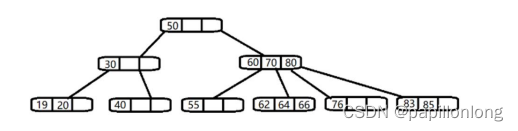
3 B 树、B+树和 B*
3.1 B 树的介绍
B-tree 树即 B 树,B 即 Balanced,平衡的意思。有人把 B-tree 翻译成 B-树,容易让人产生误解。会以为 B-树
是一种树,而 B 树又是另一种树。实际上,B-tree 就是指的 B 树。
3.2 B 树的介绍
前面已经介绍了 2-3 树和 2-3-4 树,他们就是 B 树(英语:B-tree 也写成 B-树),这里我们再做一个说明,我们在学
习 Mysql 时,经常听到说某种类型的索引是基于 B 树或者 B+树的,如图
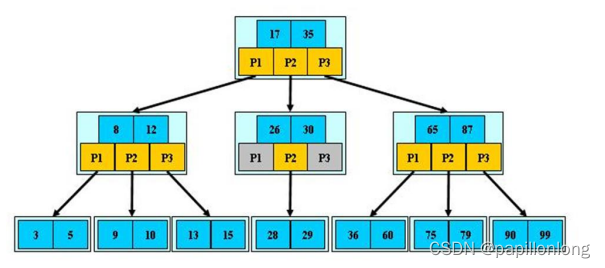
对上图的说明:
- B 树的阶:节点的最多子节点个数。比如 2-3 树的阶是 3,2-3-4 树的阶是 4
- B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询
关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点 - 关键字集合分布在整颗树中, 即叶子节点和非叶子节点都存放数据. 4) 搜索有可能在非叶子结点结束
- 其搜索性能等价于在关键字全集内做一次二分查找
3.3 B+树的介绍
B+树是 B 树的变体,也是一种多路搜索树。
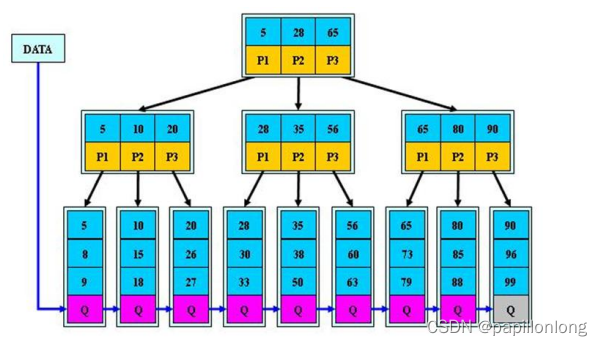
对上图的说明:
- B+树的搜索与 B 树也基本相同,区别是 B+树只有达到叶子结点才命中(B 树可以在非叶子结点命中),其性
能也等价于在关键字全集做一次二分查找 - 所有关键字都出现在叶子结点的链表中(即数据只能在叶子节点【也叫稠密索引】),且链表中的关键字(数据)
恰好是有序的。 - 不可能在非叶子结点命中
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层
- 更适合文件索引系统
- B 树和 B+树各有自己的应用场景,不能说 B+树完全比 B 树好,反之亦然.
3.4 B*树的介绍
B*树是 B+树的变体,在 B+树的非根和非叶子结点再增加指向兄弟的指针
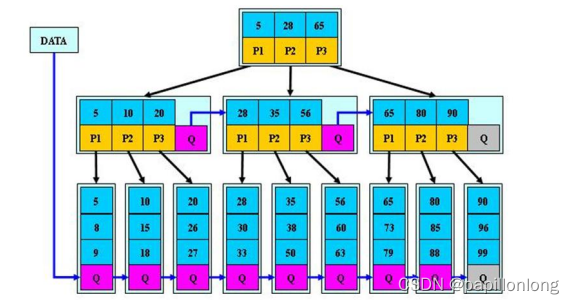
B*树的说明:
- B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为 2/3,而 B+树的块的最低使用率为的
1/2。 - 从第 1 个特点我们可以看出,B*树分配新结点的概率比 B+树要低,空间使用率更高
相关文章:

多路查找树
1.二叉树与 B 树 1.1二叉树的问题分析 二叉树的操作效率较高,但是也存在问题, 请看下面的二叉树 二叉树需要加载到内存的,如果二叉树的节点少,没有什么问题,但是如果二叉树的节点很多(比如 1 亿), 就 存在如下问题:问…...

Mybatis——注入执行sql查询、更新、新增以及建表语句
文章目录前言案例dao和mapper编写XXXmapper.xml编写编写业务层代码,进行注入调用额外扩展--创建表语句前言 在平时的项目开发中,mybatis应用非常广泛,但一般都是直接CRUD类型sql的执行。 本片博客主要说明一个另类的操作,注入sq…...

即时通讯系列-4-如何设计写扩散下的同步协议方案
1. 背景信息 上篇提到了, IM协议层是主要解决会话和消息的同步, 在实现上, 以推模式为主, 拉模式为辅. 本文Agenda: (How)如何同步(How)如何设计同步位点如何设计 Gap过大(SyncGapOverflow) 机制如何设计Ack机制总结 提示: 本系列文章不会单纯的给出结论, 希望能够分享的是&…...

tui-swipe-action组件上的按钮点击后有阴影的解决方法
大家好,我是雄雄,欢迎关注微信公众号:雄雄的小课堂。 目录 前言问题描述问题解决前言 一直未敢涉足电商领域,总觉得这里面的道道很多,又是支付、又是物流的,还涉及到金钱,所以我们所做的项目,一直都是XXXX管理系统,XXX考核系统,移动端的也是,XX健康管理平台…… 但…...

【大数据Hadoop】Hadoop 3.x 新特性总览
Hadoop 3.x 新特性剖析系列11. 概述2. 内容2.1 JDK2.2 EC技术2.3 YARN的时间线V.2服务2.3.1 伸缩性2.3.2 可用性2.3.3 架构体系2.4 优化Hadoop Shell脚本2.5 重构Hadoop Client Jar包2.6 支持等待容器和分布式调度2.7 支持多个NameNode节点2.8 默认的服务端口被修改2.9 支持文件…...

Python-第三天 Python判断语句
Python-第三天 Python判断语句一、 布尔类型和比较运算符1.布尔类型2.比较运算符二、if语句的基本格式1.if 判断语句语法2.案例三、 if else 语句1.语法2.案例四 if elif else语句1.语法五、判断语句的嵌套1.语法六、实战案例一、 布尔类型和比较运算符 1.布尔类型 布尔&…...

失手删表删库,赶紧跑路?!
在数据资源日益宝贵的数字时代公司最怕什么?人还在,库没了是粮库、车库,还是小金库?实际上,这里的“库”是指的数据库Ta是公司各类信息的保险柜小到企业官网和客户信息大到金融机构的资产数据和国家秘密即便没有跟数据…...
技术树基础——16排它平方数(Bigdecimal,int,string,数组的转换)
题目:03879 * 203879 41566646641这有什么神奇呢?仔细观察,203879 是个6位数,并且它的每个数位上的数字都是不同的,并且它平方后的所有数位上都不出现组成它自身的数字。具有这样特点的6位数还有一个,请你…...

04动手实践:手把手带你实现gRPC的Hello World
这篇文章就从实践的角度出发,带大家一起体验一下gRPC的Hello World。文中的代码将全部使用Go语言实现,使用到的示例也是GitHub上提供的grpc-go,下面我们开始: Hello World官方示例 首先我们要clone GitHub上gRPC的源代码到我们本地 git clone https://github.com/grpc/g…...

区块链技术与应用1——BTC-密码学原理
文章目录比特币中的密码学原理1. 哈希函数2. 数字签名3. 比特币中的哈希函数和数字签名简单介绍:比特币与以太坊都是以区块链技术为基础的两种加密货币,因为他们应用最广泛,所以讲区块链技术一般就讲比特币和以太坊。比特币中的密码学原理 1…...

PyTorch学习笔记:data.WeightedRandomSampler——数据权重概率采样
PyTorch学习笔记:data.WeightedRandomSampler——数据权重概率采样 torch.utils.data.WeightedRandomSampler(weights, num_samples, replacementTrue, generatorNone)功能:按给定的权重(概率)[p0,p1,…,pn−1][p_0,p_1,\dots,p_{n-1}][p0,p1,…,pn…...

SpringMVC对请求参数的处理
如何获取SpringMVC中请求中的信息 ? 默认情况下,可以直接在方法的参数中填写跟请求参数一样的名称,此时会默认接受参 数 ,如果有值,直接赋值,如果没有,那么直接给空值 。Controller RequestMapp…...

12年老外贸的经验分享
回想这12年的经历,很庆幸自己的三观一直是正确的,就是买家第一不管什么原因,只要你想退货,我都可以接受退款。不能退给上级供应商,我就自己留着,就是为了避免因为这个拒收而失去买家。不管是什么质量原因&a…...
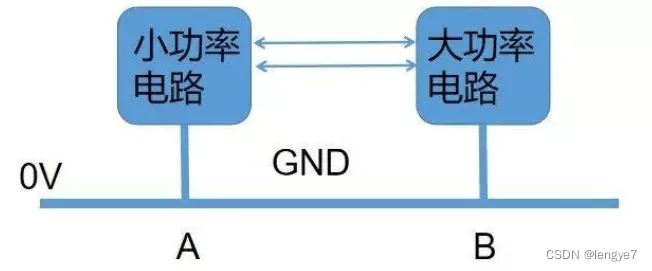
电子电路中的各种接地(接地保护与GND)
前言多年以前,雷雨天气下,建筑会遭遇雷击,从而破坏建筑以及伤害建筑内的人,为了避免雷击的伤害,人们发明了避雷针,并将避雷针接地线,从而引导雷击产生的电流经过地线流入到地下。地线࿱…...

php实现农历公历日期的相互转换
农历(Lunar calendar)和公历(Gregorian calendar)是两种不同的日历系统。公历是基于太阳和地球的运动来计算时间的,而农历是基于月亮的运动来计算时间的。农历中的月份是根据月亮的相对位置来确定的,而公历…...
基于SpringBoot的房屋租赁管理系统的设计与实现
基于SpringBoot的房屋租赁管理系统的设计与实现 1 绪论 1.1 课题来源 随着社会的不断发展以及大家生活水平的提高,越来越多的年轻人选择在大城市发展。在大城市发展就意味着要在外面有一处安身的地方。在租房的过程中,大家也面临着各种各样的问题&…...

一文带你为PySide6编译MySQL插件驱动
1.概述 最近使用PySide6开发程序,涉及与MySQL的数据交互。但是qt官方自pyqt5.12(记不太清了)以后不再提供MySQL的插件驱动,只能自己根据qt的源码编译。不过网上大部分都是qt5的MySQL驱动的编译教程。后来搜到了一个qt6的编译教程…...
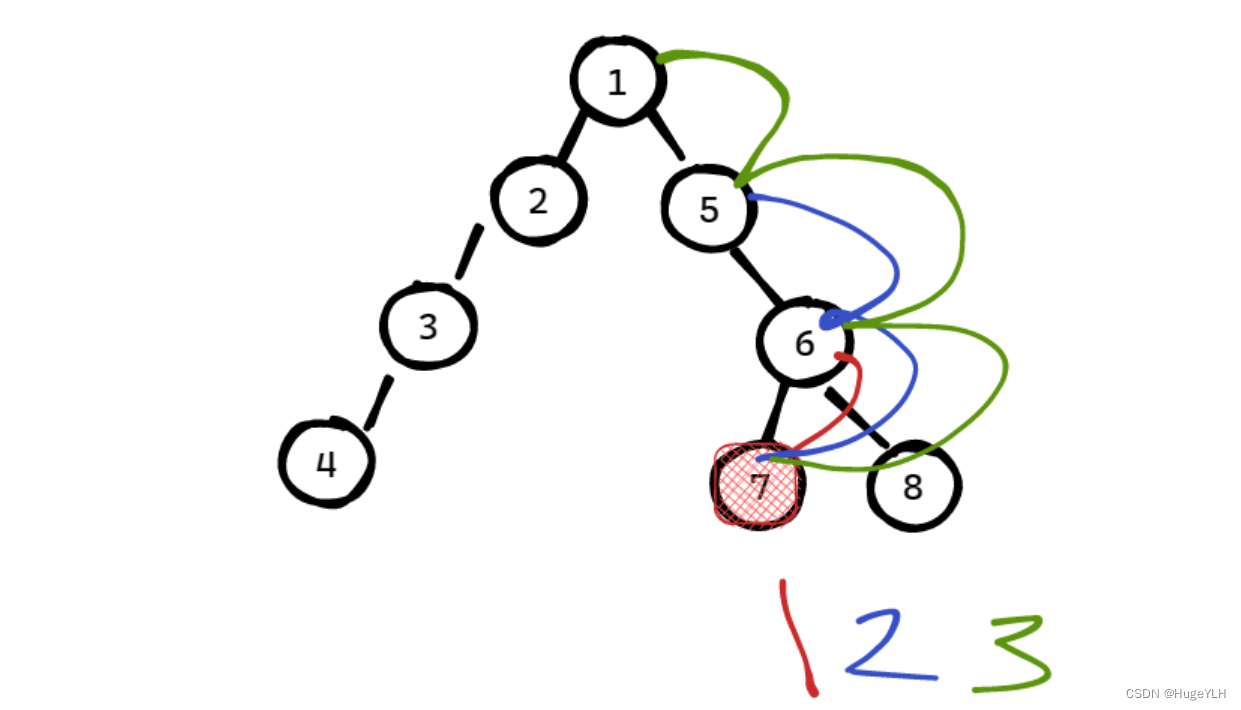
图论算法:树上倍增法解决LCA问题
文章目录树上倍增法: LCA问题树上倍增法: LCA问题 树上倍增法用于求解LCA问题是一种非常有效的方法。 倍增是什么? 简单来说,倍增就是 1 2 4 8 16 … 2^k 可以发现倍增是呈 2的指数型递增的一类数据,和二分一样&…...
 和 execute()方法有什么区别)
Java线程池中submit() 和 execute()方法有什么区别
点个关注,必回关 文章目录一. execute和submit的区别与联系1、测试代码的整体框架如下:2、首先研究Future<?> submit(Runnable task)和void execute(Runnable command),3、submit(Runnable task, T result) 方法可以使submit执行完Run…...

Vue.extend和VueComponent的关系源码解析
目录 0.概念解释 前言 需求分析 Vue.extend 编程式的使用组件 源码分析 0.概念解释 Vue.extend和VueComponent是Vuejs框架中创建组件的两种不同方式。Vue.extend方法能够让你根据Vue对象(继承)来定义一个新的可重用的组件构造器。而VueComponent方…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
