[Machine Learning] 多任务学习
文章目录
- 基于参数的MTL模型 (Parameter-based MTL Models)
- 基于特征的MTL模型 (Feature-based MTL Models)
- 基于特征的MTL模型 I:
- 基于特征的MTL模型 II:
- 基于特征和参数的MTL模型 (Feature- and Parameter-based MTL Models)
多任务学习 (Multi-task Learning, MTL) 是一种同时学习多个相关问题的方法,它通过利用这些问题之间的相关性来进行学习。

在单任务学习 (Single-Task Learning, STL) 中,每个任务有一个独立的模型,这些模型分别学习不同的任务。这里,每个任务(Task 1, Task 2, Task 3, Task 4)都有它自己的输入和独立的神经网络模型。这些模型不会共享学习到的特征或表示,它们是完全独立的。

在多任务学习中,一个单一的模型共同学习多个任务。模型共享输入层和可能还有一些隐藏层,但在最后,可以有特定于任务的输出层。通过这种方式,模型可以学习到在多个任务间共通的、有用的表示,这可以提升模型在各个任务上的性能,特别是当这些任务相关时。多任务学习还有助于提高数据利用率和学习效率,因为相同的数据和模型参数被用来解决多个问题。
这幅图用来说明的关键点是,在多任务学习中,我们期望通过任务之间的相关性来提升性能,而在单任务学习中,每个任务都是孤立地学习,无法从其他任务中学习到的信息中受益。
当任务彼此独立时,多任务学习与单任务学习相比并无优势。
对于数据不足的问题,当有多个相关任务且每个任务的训练样本有限时,多任务学习是一个很好的解决方案。
设定有 m m m个学习任务 { T i } i = 1 m \{T_i\}_{i=1}^m {Ti}i=1m,其中所有任务或其子集彼此相关,多任务学习旨在通过使用 m m m个任务中包含的知识来帮助提高模型对 T i \mathcal{T}_i Ti的学习。任务 T i \mathcal{T}_i Ti伴随着一个训练集 D i = { x j i , y j i } j = 1 n i D_i = \{ x_j^i, y_j^i \}_{j=1}^{n_i} Di={xji,yji}j=1ni。
我们的任务是为 { T i } i = 1 m \{T_i\}_{i=1}^m {Ti}i=1m学习假设。
在MTL中,我们考虑线性假设函数,表示为 h ( x ) = w T x h(x) = w^T x h(x)=wTx。对于 m m m 个不同但相关的任务,即 { T i } i = 1 m \{T_i\}^m_{i=1} {Ti}i=1m,我们定义 w i w^i wi 为第 i i i 个任务的假设,其中 i = 1 , … , m i = 1, \ldots, m i=1,…,m。
MTL的经验风险最小化算法表示为:
min W = [ w 1 , … , w m ] 1 m ∑ i = 1 m 1 n i ∑ j = 1 n i ℓ ( x j i , y j i , w i ) \min\limits_{W=[w^1,\ldots,w^m]} \frac{1}{m} \sum_{i=1}^{m} \frac{1}{n_i} \sum_{j=1}^{n_i} \ell (x^i_j, y^i_j, w^i) W=[w1,…,wm]minm1i=1∑mni1j=1∑niℓ(xji,yji,wi)
MTL模型通常由两个主要组件组成:参数共享和特征变换。参数共享是指在多个任务间共享模型参数,这样可以使不同任务互相借鉴彼此的信息,从而提高学习效率。特征变换则是指对输入数据进行变换,以找到一个更适合所有任务的表示方式。
基于参数的MTL模型 (Parameter-based MTL Models)
在这种方法中,我们考虑多个相关的任务,并且假设每个任务的假设 w i w^i wi可以表示为一个共同的基础参数 w 0 w_0 w0加上一个特定任务的偏差 Δ w i \Delta w^i Δwi。这个模型的形式化为:
min w 0 , Δ W = [ Δ w 1 , … , Δ w m ] 1 m ∑ i = 1 m 1 n i ∑ j = 1 n i ℓ ( x j i , y j i , w 0 + Δ w i ) \min_{w_0,\Delta W = [\Delta w^1, \ldots, \Delta w^m]} \frac{1}{m} \sum_{i=1}^{m} \frac{1}{n_i} \sum_{j=1}^{n_i} \ell(x^i_j, y^i_j, w_0 + \Delta w^i) w0,ΔW=[Δw1,…,Δwm]minm1i=1∑mni1j=1∑niℓ(xji,yji,w0+Δwi)
这里的 ℓ \ell ℓ是损失函数, x j i x^i_j xji和 y j i y^i_j yji是第 i i i个任务的第 j j j个训练样本及其标签。
这样,第 i i i个任务的模型参数可以表示为 w i = w 0 + Δ w i w^i = w_0 + \Delta w^i wi=w0+Δwi。全局参数 w 0 w_0 w0捕获了所有任务之间的共性,而 Δ w i \Delta w^i Δwi则捕获了任务特有的特性。我们的优化目标是最小化所有任务的总损失,同时尽可能地使得各任务参数相互接近,这通常通过添加一个正则化项 ∥ Δ W ∥ F 2 \|\Delta W\|_F^2 ∥ΔW∥F2来实现:
min w 0 , Δ W = [ Δ w 1 , … , Δ w m ] 1 m ∑ i = 1 m 1 n i ∑ j = 1 n i ℓ ( x j i , y j i , w 0 + Δ w i ) + λ ∥ Δ W ∥ F 2 \min_{w_0,\Delta W = [\Delta w^1, \ldots, \Delta w^m]} \frac{1}{m} \sum_{i=1}^{m} \frac{1}{n_i} \sum_{j=1}^{n_i} \ell(x^i_j, y^i_j, w_0 + \Delta w^i) + \lambda \|\Delta W\|_F^2 w0,ΔW=[Δw1,…,Δwm]minm1i=1∑mni1j=1∑niℓ(xji,yji,w0+Δwi)+λ∥ΔW∥F2
这个模型更好,因为它鼓励多任务学习算法具有更强的相关性。
另一个模型使用秩约束:
min W = [ w 1 , … , w m ] 1 m ∑ i = 1 m 1 n i ∑ j = 1 n i ℓ ( x j i , y j i , w i ) + λ rank ( W ) \min\limits_{W=[w^1,\ldots,w^m]} \frac{1}{m} \sum\limits_{i=1}^{m} \frac{1}{n_i} \sum\limits_{j=1}^{n_i} \ell(x^i_j, y^i_j, w^i) + \lambda \text{ rank}(W) W=[w1,…,wm]minm1i=1∑mni1j=1∑niℓ(xji,yji,wi)+λ rank(W)
基于特征的MTL模型 (Feature-based MTL Models)
在基于特征的MTL模型中,假设是从训练样例中学到的:
给定一组数据 D i = { x j i , y j i } j = 1 n i \mathcal{D}_i = \{ x_j^{i}, y_j^{i} \}_{j=1}^{n_i} Di={xji,yji}j=1ni,
我们希望通过特征映射使得任务之间更加相关。即,我们希望找到一个投影矩阵 P P P,使得 D i \mathcal{D}_i Di变换为 D i = { P T x j i , y j i } j = 1 n i \mathcal{D}_i = \{ P^T x_j^{i}, y_j^{i} \}_{j=1}^{n_i} Di={PTxji,yji}j=1ni
基于特征的MTL模型 I:
min W , P 1 m ∑ i = 1 m 1 n i ∑ j = 1 n i ℓ ( P T x j i , y j i , w i ) + λ rank ( W ) s.t. P P T = I \min_{W,P} \frac{1}{m} \sum_{i=1}^{m} \frac{1}{n_i} \sum_{j=1}^{n_i} \ell(P^T x_j^{i}, y_j^{i},w^i) + \lambda \text{rank}(W) \text{ s.t. } PP^T = I W,Pminm1i=1∑mni1j=1∑niℓ(PTxji,yji,wi)+λrank(W) s.t. PPT=I
这个损失函数计算的是映射后的特征与目标值之间的误差,并加入了正则化项以控制权重矩阵W的复杂度。损失函数以 ℓ ( P T x i j , y i j , w i ) \ell(P^T x_i^j, y_i^j, w^i) ℓ(PTxij,yij,wi) 表示, x i j x_i^j xij 是第i个任务的第j个样本的特征, y i j y_i^j yij 是对应的目标值, w i w^i wi 是第i个任务的权重向量, P P P 是一个投影矩阵,使得通过 P T x j i P^T x_j^{i} PTxji变换后的特征可以更好地为多个任务服务。
λ \lambda λ 是正则化项的权重, rank ( W ) \text{rank}(W) rank(W) 是权重矩阵的秩,用于控制模型的复杂度。
基于特征的MTL模型 II:

这是一个共享隐藏层的神经网络架构,其中隐藏层的节点可以被看作是特征提取器。
对应的优化问题考虑了一个共享参数 w 0 w_0 w0 和针对每个任务的调整参数 Δ w i \Delta w_i Δwi。
这个模型的目标是最小化包含共享参数和任务特定调整的损失函数,并通过 λ ∣ ∣ Δ W ∣ ∣ F 2 \lambda ||\Delta W||_F^2 λ∣∣ΔW∣∣F2 正则化每个任务的参数调整量。
隐藏层对于所有任务来说是共享的,这意味着模型可以学习通用的特征表示,而输出层则是特定于任务的。
基于特征和参数的MTL模型 (Feature- and Parameter-based MTL Models)
min w 0 , Δ W , P 1 m ∑ i = 1 m 1 n i ∑ j = 1 n i ℓ ( P T x j i , y j i , w 0 + Δ w i ) + λ ∥ Δ W ∥ F 2 s.t. P P T = I \min_{w_0, \Delta W,P} \frac{1}{m} \sum_{i=1}^{m} \frac{1}{n_i} \sum_{j=1}^{n_i} \ell(P^T x_j^{i}, y_j^{i},w_0 + \Delta w^i) + \lambda \|\Delta W\|_F^2 \text{ s.t. } PP^T = I w0,ΔW,Pminm1i=1∑mni1j=1∑niℓ(PTxji,yji,w0+Δwi)+λ∥ΔW∥F2 s.t. PPT=I
该模型旨在找到一个跨任务共享的特征投影( P P P)和一组针对所有任务优化的参数( w 0 w_0 w0 和 Δ W ΔW ΔW)。
-
目标函数: min w 0 , Δ W , P \min_{w_0, \Delta W,P} minw0,ΔW,P 表示我们的目标是最小化关于 w 0 w_0 w0(共享参数)、 Δ W \Delta W ΔW(任务特定参数变化)和 P P P(特征投影矩阵)的某个函数。
-
任务平均: 1 m ∑ i = 1 m \frac{1}{m} \sum_{i=1}^{m} m1∑i=1m 表示我们考虑 m m m 个不同的任务,并对这些任务的结果取平均。
-
任务内平均**: 对于每个任务 i i i, 1 n i ∑ j = 1 n i \frac{1}{n_i} \sum_{j=1}^{n_i} ni1∑j=1ni 用于对该任务中的 n i n_i ni 个样本进行平均。
-
损失函数: ℓ ( P T x j i , y j i , w 0 + Δ w i ) \ell(P^T x_j^{i}, y_j^{i},w_0 + \Delta w^i) ℓ(PTxji,yji,w0+Δwi) 是损失函数,用于量化模型预测 P T x j i P^T x_j^{i} PTxji(经过特征转换的输入)和真实标签 y j i y_j^{i} yji 之间的差异,同时考虑共享参数 w 0 w_0 w0 和任务特定参数的调整 Δ w i \Delta w^i Δwi。
-
正则化项: λ ∥ Δ W ∥ F 2 \lambda \|\Delta W\|_F^2 λ∥ΔW∥F2 是正则化项,用于防止过拟合。它通过控制任务特定参数变化的大小(使用Frobenius范数)来实现。
-
约束条件: P P T = I PP^T = I PPT=I 是一个约束条件,确保投影矩阵 P P P 是正交的。这有助于保持映射后的特征间的独立性。
相关文章:

[Machine Learning] 多任务学习
文章目录 基于参数的MTL模型 (Parameter-based MTL Models)基于特征的MTL模型 (Feature-based MTL Models)基于特征的MTL模型 I:基于特征的MTL模型 II: 基于特征和参数的MTL模型 (Feature- and Parameter-based MTL Models) 多任务学习 (Multi-task Lear…...

【C语言从入门到放弃 6】递归,强制类型转换,可变参数和错误处理详解
C语言是一种功能强大的编程语言,具有许多高级特性,包括强制类型转换,递归,可变参数和错误处理。在本文中,我们将深入了解这些特性,并提供简单的示例来帮助理解。 递归 递归是一种函数调用自身的技术&…...

使用LLama和ChatGPT为多聊天后端构建微服务
微服务架构便于创建边界明确定义的灵活独立服务。这种可扩展的方法使开发人员能够在不影响整个应用程序的情况下单独维护和完善服务。然而,若要充分发挥微服务架构的潜力、特别是针对基于人工智能的聊天应用程序,需要与最新的大语言模型(LLM&…...
CSS3 用户界面、图片、按钮
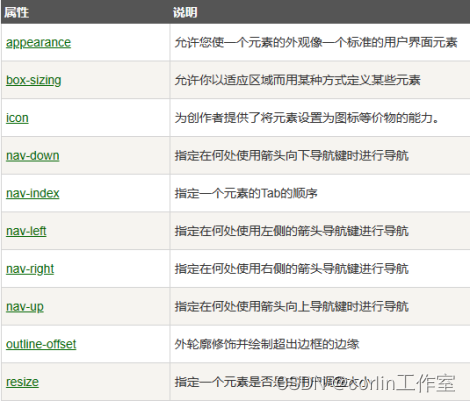
一、CSS3用户界面: 在CSS3中,增加了一些新的用户界面特性来调整元素尺寸、框尺寸和外边框。CSS3用户界面属性:resize、box-sizing、outline-offset。 1、resize: resize属性指定一个元素是否应该由用户去调整大小。 <style…...

说说对Redux中间件的理解?常用的中间件有哪些?实现原理?
一、是什么 中间件(Middleware)是介于应用系统和系统软件之间的一类软件,它使用系统软件所提供的基础服务(功能),衔接网络上应用系统的各个部分或不同的应用,能够达到资源共享、功能共享的目的…...
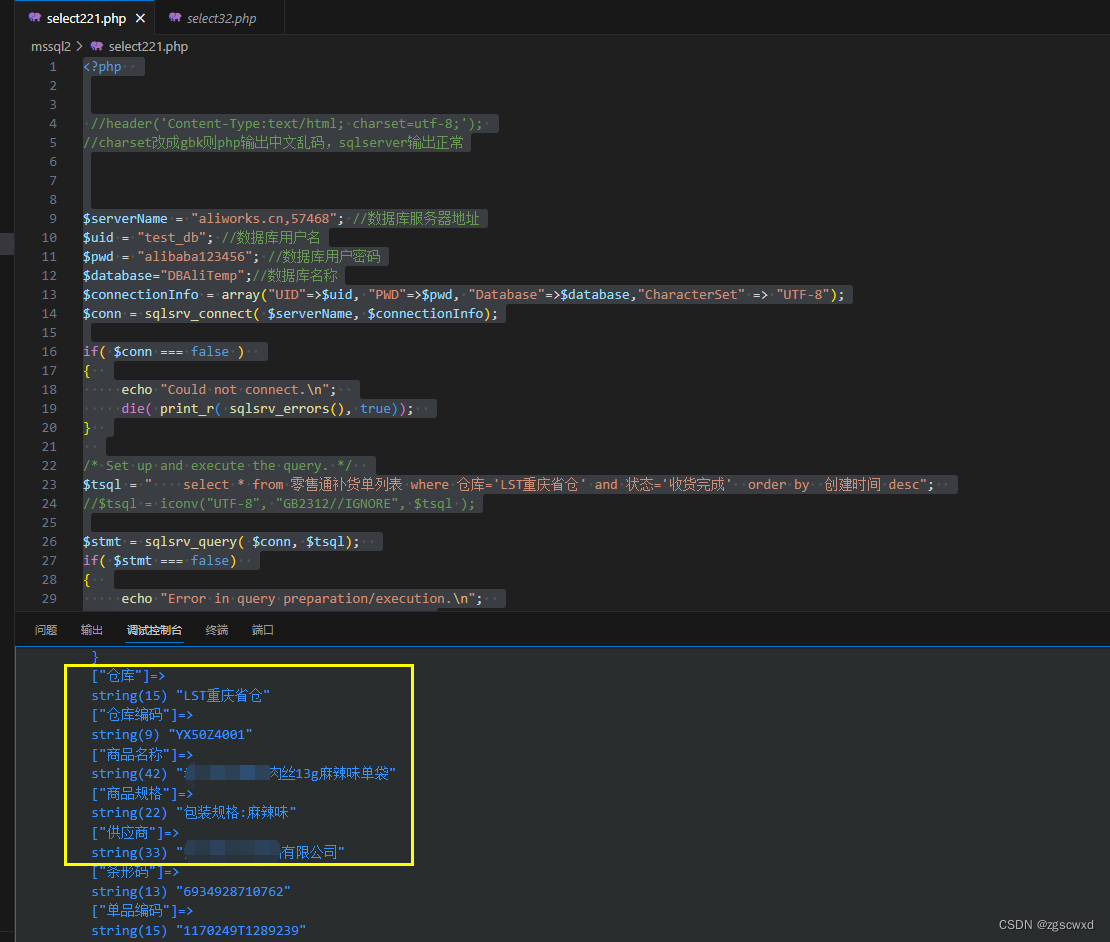
【已验证】php配置连接sql server中文乱码(解决方法)更改utf-8格式
解决数据库中的中文数据在页面显示乱码的问题 在连接的$connectionInfo中设置"CharacterSet" > "UTF-8",指定编码方式即可 $connectionInfo array("UID">$uid, "PWD">$pwd, "Database">$database…...

《未来之路:技术探索与梦想的追逐》
创作纪念日 日期:2023年07月05日文章标题:《从零开始-与大语言模型对话学技术-gradio篇(1)》成为创作者第128天 在这个平凡的一天,我撰写了自己的第一篇技术博客,题为《从零开始-与大语言模型对话学技术-…...

vue3 自动导入composition-apiI和组件
1.api的自动导入 常规写法: <script setup>import { ref, reactive, onMounted, computed ,watch } from vue;import { useRouter } from "vue-router";const router useRouter();const person reactive ({name:张三,age…...

LeetCode15-三数之和
本文最精华的就是下面的视频讲解! 🔗:参考的视频讲解 class Solution {public List<List<Integer>> threeSum(int[] nums) {List<List<Integer>> ans new ArrayList<>();Arrays.sort(nums);int nnums.length;int i0,j0,k0,sum0;for(…...
)
安全物理环境(设备和技术注解)
网络安全等级保护相关标准参考《GB/T 22239-2019 网络安全等级保护基本要求》和《GB/T 28448-2019 网络安全等级保护测评要求》 密码应用安全性相关标准参考《GB/T 39786-2021 信息系统密码应用基本要求》和《GM/T 0115-2021 信息系统密码应用测评要求》 1物理位置选择 1.1机房…...
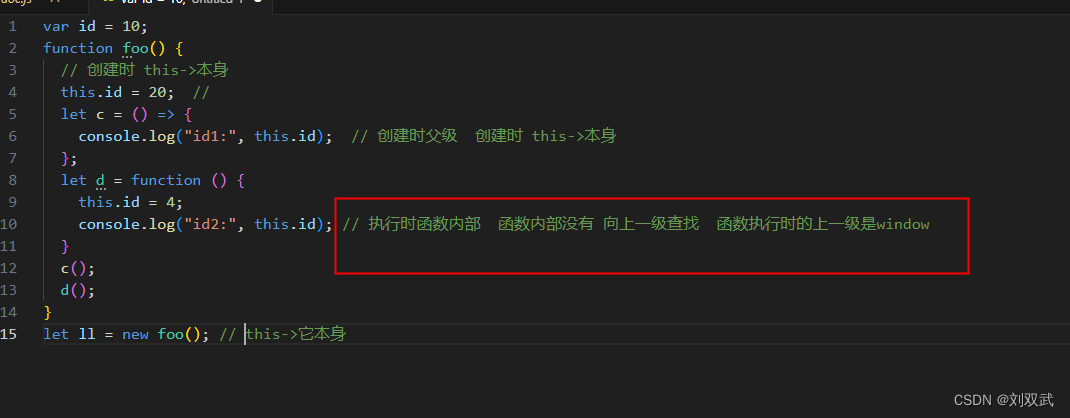
箭头函数 跟匿名函数this的指向问题
var id 10; function foo() {// 创建时 this->windowthis.id 20; // 等价于 window.id 20let c () > {console.log("id1:", this.id); // 创建时父级 创建时 this->window};let d function () {console.log("id2:", this.id); // 执行时本…...

Java Stream:List分组成Map或LinkedHashMap
在Java中,使用Stream API可以轻松地对集合进行操作,包括将List转换为Map或LinkedHashMap。本篇博客将演示如何利用Java Stream实现这两种转换,同时假设List中的元素是User对象。 1. 数据准备 List<User> list new ArrayList<>(…...
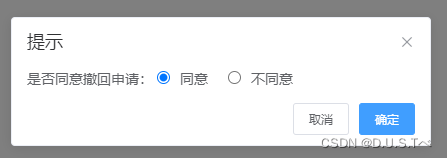
vue2+elementui使用MessageBox 弹框$msgbox自定义VNode内容:实现radio
虽说实现下面的效果,用el-dialog很轻松就能搞定。但是这种简单的交互,我更喜欢使用MessageBox。 话不多说,直接上代码~ <el-button type"primary" size"mini" click"handleApply()" >处理申请</el-b…...

OC 实现手指滑动拖动View
RPReplay_Final1699613924 实现手指滑动拖动View 支持手势移动的控件 支持 Masonry frame 布局 使用富文本 也支持自动高度 核心代码 - (void)handlePanGesture:(UIPanGestureRecognizer *)p {CGPoint panPoint [p locationInView:self.view];CGPoint currentViewPoint _dr…...

多级缓存之实现多级缓存
多级缓存的实现离不开Nginx编程,而Nginx编程又离不开OpenResty。 1. OpenResty快速入门 我们希望达到的多级缓存架构如图: 其中: windows上的nginx用来做反向代理服务,将前端的查询商品的ajax请求代理到OpenResty集群 OpenRest…...

React【axios、全局处理、 antd UI库、更改主题、使用css module的情况下修改第三方库的样式、支持sass less】(十三)
文件目录 Proxying in Development http-proxy-middleware fetch_get fetch 是否成功 axios 全局处理 antd UI库 更改主题 使用css module的情况下修改第三方库的样式 支持sass & less Proxying in Development 在开发模式下,如果客户端所在服务器跟后…...
在gitlab中指定自定义 CI/CD 配置文件
文章目录 1. 介绍2. 配置操作3. 配置场景3.1 CI/CD 配置文件在当前项目step1:在当前项目中创建目录,编写流水线文件存放在该目录中step2:在当前项目中配置step3:运行流水线测试 3.2 CI/CD 配置文件位于外部站点上step1:…...
(论文阅读22/100)Learning a Deep Compact Image Representation for Visual Tracking
文献阅读笔记 简介 题目 Learning a Deep Compact Image Representation for Visual Tracking 作者 N Wang, DY Yeung 原文链接 Learning a Deep Compact Image Representation for Visual Tracking (neurips.cc) 关键词 Object tracking、DLT、SDAE 研究问题 track…...

浅谈设计模式
文章目录 一、单例模式 1.饿汉模式 2.懒汉模式 二、工厂模式 三、建造者模式 四、代理模式 设计模式是前辈们对代码开发的总结,是解决特定问题的一系列套路。它不是语法规定,而是一套用来提高代码可复用性、可维护性、可读性、稳健性以及安全性的解…...

企业年会/年终活动如何邀请媒体记者报道?
媒体邀约是企业或组织进行宣传的重要手段之一。通过邀请媒体参加活动,可以增加活动的曝光度和知名度,吸引更多的关注和参与。同时,媒体报道还可以提高企业或组织的权威性和可信度,从而让公众更容易接受其传达的信息。 企业年会或…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
