AM@方向导数概念和定理
文章目录
- abstract
- 方向导数
- 二元函数方向导数
- 偏导数是方向导数的特例
- 偏导数存在一定有对应的方向导数存在
- 方向导数存在不一定有偏导数存在
- 例
- 三元函数方向导数
- 例
- 方向导数存在定理和计算公式
- 证明
- 二元函数
- 三元函数
abstract
- 方向导数的概念,定理和计算公式
- 方向导数是对偏导的补充,其本质上是一个极限问题,而其计算可以转化为偏导的计算和方向余弦的计算,表现为偏导数构成的向量和方向余弦构成的向量作数量积
方向导数
-
偏导数反映的是函数(自变量)沿着坐标轴方向的变换率
-
为研究多元函数在某一点P沿任意方向(某个方向)的变化率,偏导数无法满足要求,因此引入多元函数的方向导数的概念
- 例如,设 f ( P ) f(P) f(P)表示某物体内点P的温度,那么这个物体的热传导就依赖于温度沿某些方向的变化率
- 预测某地的风向和风力,就需要知道气压在该处沿某些方向的变化率
二元函数方向导数
- 设 l l l为 x O y xOy xOy平面上以 P 0 ( x 0 , y 0 ) P_{0}(x_0,y_0) P0(x0,y0)为始点的一条射线,设其倾斜角为 α ( α ∈ [ 0 , π ) ) \alpha(\alpha\in[0,\pi)) α(α∈[0,π)),则 e l \bold{e_{l}} el= ( cos α , cos β ) (\cos\alpha,\cos\beta) (cosα,cosβ)是与 l l l同方向的单位向量
- α + β = π 2 \alpha+\beta=\frac{\pi}{2} α+β=2π, cos β = sin α \cos\beta=\sin\alpha cosβ=sinα, cos 2 α + cos 2 β \cos^2\alpha+\cos^2\beta cos2α+cos2β= cos 2 α + sin 2 α = 1 \cos^{2}\alpha+\sin^2\alpha=1 cos2α+sin2α=1
- 由直线的参数方程公式,射线所在直线的参数方程为 x = x 0 + t cos α x=x_0+t\cos\alpha x=x0+tcosα; y = y 0 + t cos β y=y_0+t\cos\beta y=y0+tcosβ,其中 t t t为任意常数;而此处要求射线的方程,需要限制 t ⩾ 0 t\geqslant{0} t⩾0
- 设函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 P 0 P_{0} P0的某个邻域 U ( P 0 ) U(P_{0}) U(P0)内有定义, P ( x 0 + t cos α , y 0 + t cos β ) P(x_0+t\cos\alpha,y_0+t\cos\beta) P(x0+tcosα,y0+tcosβ)为 l l l上的另一点,切 P ∈ U ( P 0 ) P\in{U}(P_{0}) P∈U(P0)
- 若记函数增量 Δ z \Delta{z} Δz= f ( x 0 + t cos α , y 0 + t cos β ) − f ( x 0 , y 0 ) f(x_0+t\cos\alpha,y_0+t\cos\beta)-f(x_0,y_0) f(x0+tcosα,y0+tcosβ)−f(x0,y0); P → P 0 P\to{P_0} P→P0的距离 ∣ P P 0 ∣ = t |PP_{0}|=t ∣PP0∣=t
- lim t → 0 + Δ z t \lim\limits_{t\to{0^{+}}}{\frac{\Delta{z}}{t}} t→0+limtΔz极限存在,则称该极限为 f ( x , y ) f(x,y) f(x,y)在点 P 0 ( x 0 , y 0 ) P_{0}(x_0,y_0) P0(x0,y0)沿方向 l l l的方向导数,记为 ∂ f ∂ l ∣ ( x 0 , y 0 ) \frac{\partial{f}}{\partial{l}}|_{(x_0,y_0)} ∂l∂f∣(x0,y0)
- 即 ∂ f ∂ l ∣ ( x 0 , y 0 ) \frac{\partial{f}}{\partial{l}}|_{(x_0,y_0)} ∂l∂f∣(x0,y0)= lim t → 0 + Δ z t \lim\limits_{t\to{0^{+}}}{\frac{\Delta{z}}{t}} t→0+limtΔz
(1)
- 由方向导数的定义可知,式(1)就是 f ( x , y ) f(x,y) f(x,y)在点 P 0 P_{0} P0处沿着方向 l l l的变化率(射线 l l l方向的变化率)
- 方向导数本质是求极限
偏导数是方向导数的特例
偏导数存在一定有对应的方向导数存在
- 若函数 f ( x , y ) f(x,y) f(x,y)在点 P 0 P_0 P0的偏导数存在,沿 x x x轴正方向同向的一个单位向量为 e l \bold{e}_{l} el= i \bold{i} i= ( 1 , 0 ) (1,0) (1,0),则 ∂ f ∂ l ∣ ( x 0 , y 0 ) \frac{\partial{f}}{\partial{l}}|_{(x_0,y_0)} ∂l∂f∣(x0,y0)= f x ( x 0 , y 0 ) f_{x}(x_0,y_0) fx(x0,y0)
- 此时 Δ z \Delta{z} Δz= f ( x 0 + t , y 0 + 0 t ) − f ( x 0 , y 0 ) f(x_0+t,y_0+0t)-f(x_0,y_0) f(x0+t,y0+0t)−f(x0,y0)= f ( x 0 + t , y 0 ) − f ( x 0 , y 0 ) f(x_0+t,y_0)-f(x_0,y_0) f(x0+t,y0)−f(x0,y0)
- 同理,若 e l \bold{e}_{l} el= j = ( 0 , 1 ) \bold{j}=(0,1) j=(0,1),则 ∂ f ∂ l ∣ ( x 0 , y 0 ) \frac{\partial{f}}{\partial{l}}|_{(x_0,y_0)} ∂l∂f∣(x0,y0)= f y ( x 0 , y 0 ) f_{y}(x_0,y_0) fy(x0,y0)
- 此时 Δ z \Delta{z} Δz= f ( x 0 + 0 t , y 0 + t ) − f ( x 0 , y 0 ) f(x_0+0t,y_0+t)-f(x_0,y_0) f(x0+0t,y0+t)−f(x0,y0)= f ( x 0 , y 0 + t ) − f ( x 0 , y 0 ) f(x_0,y_0+t)-f(x_0,y_0) f(x0,y0+t)−f(x0,y0)
方向导数存在不一定有偏导数存在
- 若 e l = i \bold{e}_{l}=\bold{i} el=i, ∂ f ∂ l ∣ ( x 0 , y 0 ) \frac{\partial{f}}{\partial{l}}|_{(x_0,y_0)} ∂l∂f∣(x0,y0)存在,未必有 ∂ f ∂ x ∣ ( x 0 , y 0 ) \frac{\partial{f}}{\partial{x}}|_{(x_0,y_0)} ∂x∂f∣(x0,y0)= f x ( x 0 , y 0 ) f_{x}(x_0,y_0) fx(x0,y0)存在
- 例如: z = x 2 + y 2 z=\sqrt{x^2+y^2} z=x2+y2在点 O ( 0 , 0 ) O(0,0) O(0,0)处沿 l = i l=\bold{i} l=i的方向的方向导数 ∂ f ∂ l ∣ ( 0 , 0 ) \frac{\partial{f}}{\partial{l}}|_{(0,0)} ∂l∂f∣(0,0)=1
- 由方向导数的定义可以计算方向导数,但是这很不方便,后面介绍使用方向导数存在定理和计算公式
- 这里先用定义计算: Δ z = f ( x 0 + t , y 0 ) − f ( x 0 , y 0 ) \Delta_{z}=f(x_0+t,y_0)-f(x_0,y_0) Δz=f(x0+t,y0)−f(x0,y0)= f ( t , 0 ) − f ( 0 , 0 ) f(t,0)-f(0,0) f(t,0)−f(0,0)= ∣ t ∣ − 0 |t|-0 ∣t∣−0= t t t, ( t > 0 ) (t>0) (t>0)
- 从而 lim t → 0 + Δ z t \lim\limits_{t\to{0^{+}}}{\frac{\Delta{z}}{t}} t→0+limtΔz=1,即 ∂ f ∂ l ∣ ( 0 , 0 ) \frac{\partial{f}}{\partial{l}}|_{(0,0)} ∂l∂f∣(0,0)=1
- 而 ∂ f ∂ x ∣ ( 0 , 0 ) \frac{\partial{f}}{\partial{x}}|_{(0,0)} ∂x∂f∣(0,0)不存在(因为 ∂ f ∂ x \frac{\partial{f}}{\partial{x}} ∂x∂f= x x 2 + y 2 \frac{x}{\sqrt{x^2+y^2}} x2+y2x,在 ( 0 , 0 ) (0,0) (0,0)处没有定义)
- 例如: z = x 2 + y 2 z=\sqrt{x^2+y^2} z=x2+y2在点 O ( 0 , 0 ) O(0,0) O(0,0)处沿 l = i l=\bold{i} l=i的方向的方向导数 ∂ f ∂ l ∣ ( 0 , 0 ) \frac{\partial{f}}{\partial{l}}|_{(0,0)} ∂l∂f∣(0,0)=1
例
-
求函数 z = x e 2 y z=xe^{2y} z=xe2y在点 P ( 1 , 0 ) P(1,0) P(1,0)处,沿从点P到Q(2,-1)的方向的方向导数值
-
方向 l l l,即 P Q → = ( 2 − 1 , − 1 − 0 ) = ( 1 , − 1 ) \overrightarrow{PQ}=(2-1,-1-0)=(1,-1) PQ=(2−1,−1−0)=(1,−1)的方向
-
单位向量 l 0 = 1 1 2 + ( − 1 ) 2 ( 1 , − 1 ) = ( 1 2 , − 1 2 ) l_0=\frac{1}{\sqrt{1^2+(-1)^2}}(1,-1)=(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}) l0=12+(−1)21(1,−1)=(21,−21)
- cos α = 1 2 \cos{\alpha}=\frac{1}{\sqrt{2}} cosα=21
- cos β = − 1 2 \cos{\beta}=-\frac{1}{\sqrt{2}} cosβ=−21
-
∂ z ∂ x ∣ P = e 2 y ∣ ( 1 , 0 ) = 1 \left.\frac{\partial{z}}{\partial{x}}\right|_P=e^{2y}|_{(1,0)}=1 ∂x∂z P=e2y∣(1,0)=1; ∂ z ∂ y ∣ P = 2 x e 2 y ∣ ( 1 , 0 ) = 2 \left.\frac{\partial{z}}{\partial{y}}\right|_P=2xe^{2y}|_{(1,0)}=2 ∂y∂z P=2xe2y∣(1,0)=2
-
∂ z ∂ l \frac{\partial{z}}{\partial{l}} ∂l∂z= ∂ z ∂ x ∣ P cos α + ∂ z ∂ y ∣ P cos β \left.\frac{\partial{z}} {\partial{x}}\right|_P\cos{\alpha} +\left.\frac{\partial{z}}{\partial{y}}\right|_P\cos{\beta} ∂x∂z Pcosα+∂y∂z Pcosβ= 1 × 1 2 + 2 × − 1 2 = − 2 2 1\times{\frac{1}{\sqrt{2}}}+2\times{-\frac{1}{\sqrt{2}}}=-\frac{\sqrt{2}}{2} 1×21+2×−21=−22
-
三元函数方向导数
-
对于三元函数 u = f ( x , y , z ) u=f(x,y,z) u=f(x,y,z)来说,它在空间一点 P 0 ( x 0 , y 0 , z 0 ) P_{0}(x_0,y_0,z_0) P0(x0,y0,z0)沿某 P 0 P_0 P0为始点的射线 l l l的方向 e l \bold{e}_{l} el= ( cos α , cos β , cos γ ) (\cos\alpha,\cos\beta,\cos\gamma) (cosα,cosβ,cosγ)的方向导数为 ∂ f ∂ l ∣ ( x 0 , y 0 ) \frac{\partial{f}}{\partial{l}}|_{(x_0,y_0)} ∂l∂f∣(x0,y0)= lim t → 0 + Δ u t \lim\limits_{t\to{0^{+}}} \frac{\Delta{u}}{t} t→0+limtΔu
(1)- 其中 Δ u \Delta{u} Δu= f ( x 0 + t cos α , y 0 + t cos β , z 0 + t cos γ ) − f ( x 0 , y 0 , z 0 ) f(x_0+t\cos\alpha,y_0+t\cos\beta,z_0+t\cos\gamma)-f(x_0,y_0,z_0) f(x0+tcosα,y0+tcosβ,z0+tcosγ)−f(x0,y0,z0)
-
若式(1)极限存在,则称该极限为 u = f ( x , y , z ) u=f(x,y,z) u=f(x,y,z)在点 P 0 P_{0} P0沿方向 l l l的方向导数,记为 ∂ f ∂ l ∣ ( x 0 , y 0 , z 0 ) \frac{\partial{f}}{\partial{l}}|_{(x_0,y_0,z_0)} ∂l∂f∣(x0,y0,z0)
例
- 设多元一次函数 f ( x , y , z ) = a x + b y + c z f(x,y,z)=ax+by+cz f(x,y,z)=ax+by+cz,向量 l l l的方向余弦为 cos α , cos β , cos γ \cos{\alpha},\cos{\beta},\cos{\gamma} cosα,cosβ,cosγ
- 设点 P ( x , y , z ) P(x,y,z) P(x,y,z), P ′ ( x + Δ x , y + Δ y , z + Δ z ) P'(x+\Delta{x},y+\Delta{y},z+\Delta{z}) P′(x+Δx,y+Δy,z+Δz)都是 f ( x , y , z ) f(x,y,z) f(x,y,z)上的点
- Δ f \Delta{f} Δf= f ( x + Δ x , y + Δ y , z + Δ z ) f(x+\Delta{x},y+\Delta{y},z+\Delta{z}) f(x+Δx,y+Δy,z+Δz)- f ( x , y , z ) f(x,y,z) f(x,y,z)= a ( x + Δ x ) + b ( y + Δ y ) + c ( z + Δ z ) a(x+\Delta{x})+b(y+\Delta{y})+c(z+\Delta{z}) a(x+Δx)+b(y+Δy)+c(z+Δz)- ( a x + b y + c z ) (ax+by+cz) (ax+by+cz)= a Δ x + b Δ y + c Δ z a\Delta{x}+b\Delta{y}+c\Delta{z} aΔx+bΔy+cΔz
- f ( x , y , z ) f(x,y,z) f(x,y,z)沿 l l l方向的平均变化率为 Δ f ∣ P P ′ ∣ \frac{\Delta{f}}{|PP'|} ∣PP′∣Δf= 1 ∣ P P ′ ∣ ( a Δ x + b Δ y + c Δ z ) \frac{1}{|PP'|}(a\Delta{x}+b\Delta{y}+c\Delta{z}) ∣PP′∣1(aΔx+bΔy+cΔz)
-
( Δ x , Δ y , Δ z ) (\Delta{x},\Delta{y},\Delta{z}) (Δx,Δy,Δz)= ( ∣ P P ′ ∣ cos α , ∣ P P ′ ∣ cos β , ∣ P P ′ ∣ cos γ ) (|PP'|\cos{\alpha},|PP'|\cos{\beta},|PP'|\cos{\gamma}) (∣PP′∣cosα,∣PP′∣cosβ,∣PP′∣cosγ)
-
a Δ x + b Δ y + c Δ z a\Delta{x}+b\Delta{y}+c\Delta{z} aΔx+bΔy+cΔz= ( a ∣ P P ′ ∣ cos α + b ∣ P P ′ ∣ cos β + c ∣ P P ′ ∣ cos γ ) (a|PP'|\cos{\alpha}+b|PP'|\cos{\beta}+c|PP'|\cos{\gamma}) (a∣PP′∣cosα+b∣PP′∣cosβ+c∣PP′∣cosγ)
-
Δ f ∣ P P ′ ∣ \frac{\Delta{f}}{|PP'|} ∣PP′∣Δf= a cos α + b cos β + c cos γ a\cos{\alpha}+b\cos{\beta}+c\cos{\gamma} acosα+bcosβ+ccosγ;
-
令 t = ∣ P P ′ ∣ t=|PP'| t=∣PP′∣, lim t → 0 Δ f t \lim\limits_{t\to{0}}{\frac{\Delta{f}}{t}} t→0limtΔf= a cos α + b cos β + c cos γ a\cos{\alpha}+b\cos{\beta}+c\cos{\gamma} acosα+bcosβ+ccosγ,所以 ∂ f ∂ l \frac{\partial{f}}{\partial{l}} ∂l∂f= a cos α + b cos β + c cos γ a\cos{\alpha}+b\cos{\beta}+c\cos{\gamma} acosα+bcosβ+ccosγ
(1)
-
- 这表明,一次函数沿 l l l方向的方向导数不随点的位置而改变
- 但是沿不同方向的方向导数一般不同(方向余弦发生改变)
方向导数存在定理和计算公式
- 若函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 P ( x 0 , y 0 , z 0 ) P{(x_0,y_0,z_0}) P(x0,y0,z0)可微分,那么函数在该点沿任意方向 l l l的方向导数存在,且 ∂ f ∂ l ∣ ( x 0 , y 0 ) \frac{\partial{f}}{\partial{l}}|_{(x_0,y_0)} ∂l∂f∣(x0,y0)= f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β f_{x}(x_0,y_{0})\cos\alpha+f_{y}(x_0,y_0)\cos\beta fx(x0,y0)cosα+fy(x0,y0)cosβ
(0)- 其中 cos α , cos β \cos\alpha,\cos\beta cosα,cosβ是方向 l l l方向余弦;直线 l l l在坐标面 x O y xOy xOy内,所以若要按空间直线处理, cos γ \cos\gamma cosγ=0
- 类似的,若函数 u = f ( x , y , z ) u=f(x,y,z) u=f(x,y,z)在点 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0)为微分,则函数在该点验证方向 e l \bold{e}_{l} el= ( cos α , cos β , cos γ ) (\cos\alpha,\cos\beta,\cos\gamma) (cosα,cosβ,cosγ)的方向导数为 ∂ f ∂ l ∣ ( x 0 , y 0 , z 0 ) \frac{\partial{f}}{\partial{l}}|_{(x_0,y_0,z_0)} ∂l∂f∣(x0,y0,z0)= f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β + f z ( x 0 , y 0 , z 0 ) cos γ f_{x}(x_0,y_0)\cos\alpha+f_{y}(x_0,y_0)\cos\beta+f_{z}(x_0,y_0,z_0)\cos\gamma fx(x0,y0)cosα+fy(x0,y0)cosβ+fz(x0,y0,z0)cosγ
证明
二元函数
- 由假设, f ( x , y ) f(x,y) f(x,y)在点 P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0(x0,y0)可微分,所以 Δ z \Delta{z} Δz= f ( x 0 + Δ x , y 0 + Δ y ) f(x_0+\Delta{x},y_0+\Delta{y}) f(x0+Δx,y0+Δy)- f ( x 0 , y 0 ) f(x_0,y_0) f(x0,y0)= f x ( x 0 , y 0 ) Δ x f_{x}(x_0,y_0)\Delta{x} fx(x0,y0)Δx+ f y ( x 0 , y 0 ) Δ y f_{y}(x_0,y_0)\Delta{y} fy(x0,y0)Δy+ o ( ρ ) o(\rho) o(ρ)
(1);其中 ρ = ( Δ x ) 2 + ( Δ y ) 2 \rho=\sqrt{(\Delta{x})^2+(\Delta{y})^2} ρ=(Δx)2+(Δy)2,但点 ( x 0 + Δ x , y 0 + Δ y ) (x_0+\Delta{x},y_0+\Delta{y}) (x0+Δx,y0+Δy)在以 P 0 P_0 P0为始点的射线 l l l上时,自变量 x , y x,y x,y的增量之间存在确定关系,应有 Δ x = t cos α \Delta{x}=t\cos\alpha Δx=tcosα, Δ y = t cos β \Delta{y}=t\cos\beta Δy=tcosβ, ρ = ( Δ x ) 2 + ( Δ y ) 2 = t \rho=\sqrt{(\Delta{x})^2+(\Delta{y})^2}=t ρ=(Δx)2+(Δy)2=t- 式(1)改写为 Δ z \Delta{z} Δz= f x ( x 0 , y 0 ) t cos α + f y ( x 0 , y 0 ) t cos α + o ( t ) f_{x}(x_0,y_0){t\cos\alpha}+f_{y}(x_0,y_0)t\cos\alpha+o(t) fx(x0,y0)tcosα+fy(x0,y0)tcosα+o(t)
- 所以 lim t → 0 + Δ z t \lim\limits_{t\to{0^{+}}}\frac{\Delta{z}}{t} t→0+limtΔz= lim t → 0 + f x ( x 0 , y 0 ) t cos α + f y ( x 0 , y 0 ) t cos α + o ( t ) t \lim\limits_{t\to{0^{+}}} \frac{f_{x}(x_0,y_0){t\cos\alpha}+f_{y}(x_0,y_0)t\cos\alpha+o(t)}{t} t→0+limtfx(x0,y0)tcosα+fy(x0,y0)tcosα+o(t)= f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β f_{x}(x_0,y_0)\cos\alpha+f_{y}(x_0,y_0)\cos\beta fx(x0,y0)cosα+fy(x0,y0)cosβ
(2)’ - 定理和计算公式(0)得证
三元函数
-
设 P ′ ( x 0 + Δ x , y 0 + Δ y , z 0 + Δ z ) P'(x_0+\Delta{x},y_0+\Delta{y},z_0+\Delta{z}) P′(x0+Δx,y0+Δy,z0+Δz)是 l l l上的点,则 l l l的方向余弦可以表示为:
- cos α = Δ x ∣ P P ′ ∣ \cos{\alpha}=\frac{\Delta{x}}{|PP'|} cosα=∣PP′∣Δx
- cos β = Δ y ∣ P P ′ ∣ \cos{\beta}=\frac{\Delta{y}}{|PP'|} cosβ=∣PP′∣Δy
- cos γ = Δ z ∣ P P ′ ∣ \cos{\gamma}=\frac{\Delta{z}}{|PP'|} cosγ=∣PP′∣Δz
- ∣ P P ′ ∣ = ( Δ x ) 2 + ( Δ y ) 2 + ( Δ z ) 2 |PP'|=\sqrt{(\Delta{x})^2+(\Delta{y})^2+(\Delta{z})^2} ∣PP′∣=(Δx)2+(Δy)2+(Δz)2
-
由假设的 f ( x , y , z ) f(x,y,z) f(x,y,z)可微,由可微的定义:
-
f ( P ′ ) − f ( P ) = f x ( P 0 ) Δ x + f y ( P 0 ) Δ y + f z ( P 0 ) Δ z + o ( ( Δ x ) 2 + ( Δ y ) 2 + ( Δ z ) 2 ) = f x ( P 0 ) Δ x + f y ( P 0 ) Δ y + f z ( P 0 ) Δ z + o ( ∣ P P ′ ∣ ) \begin{aligned} f(P')-f(P)=&f_x(P_0)\Delta{x}+f_y(P_0)\Delta{y}+f_z(P_0)\Delta{z} \\&+o(\sqrt{(\Delta{x})^2+(\Delta{y})^2+(\Delta{z})^2}) \\ =&f_x(P_0)\Delta{x}+f_y(P_0)\Delta{y}+f_z(P_0)\Delta{z}+o(|PP'|) \end{aligned} f(P′)−f(P)==fx(P0)Δx+fy(P0)Δy+fz(P0)Δz+o((Δx)2+(Δy)2+(Δz)2)fx(P0)Δx+fy(P0)Δy+fz(P0)Δz+o(∣PP′∣)
-
对两边同时除以 ∣ P P ′ ∣ |PP'| ∣PP′∣
- f ( P ′ ) − f ( P ) ∣ P P ′ ∣ = f x ( P 0 ) Δ x + f y ( P 0 ) Δ y + f z ( P 0 ) Δ z + o ( ∣ P P ′ ∣ ) ∣ P P ′ ∣ = f x ( P 0 ) cos α + f y ( P 0 ) cos β + f z ( P 0 ) cos γ + o ( ∣ P P ′ ∣ ) ∣ P P ′ ∣ \frac{f(P')-f(P)}{|PP'|} =\frac{f_x(P_0)\Delta{x}+f_y(P_0)\Delta{y}+f_z(P_0)\Delta{z}+o(|PP'|)}{|PP'|} \\=f_x(P_0)\cos{\alpha}+f_y(P_0)\cos{\beta}+f_z(P_0)\cos{\gamma}+\frac{o(|PP'|)}{|PP'|} ∣PP′∣f(P′)−f(P)=∣PP′∣fx(P0)Δx+fy(P0)Δy+fz(P0)Δz+o(∣PP′∣)=fx(P0)cosα+fy(P0)cosβ+fz(P0)cosγ+∣PP′∣o(∣PP′∣)
-
对两边取极限:
- ∂ f ∂ l = lim P ′ → P 0 f ( P ′ ) − f ( P ) ∣ P P ′ ∣ = lim P ′ → P 0 ( f x ( P 0 ) cos α + f y ( P 0 ) cos β + f z ( P 0 ) cos γ + o ( ∣ P P ′ ∣ ) ∣ P P ′ ∣ ) = f x ( P 0 ) cos α + f y ( P 0 ) cos β + f z ( P 0 ) cos γ \begin{aligned} \frac{\partial{f}}{\partial{l}} =&\lim_{P'\to{P_0}}{\frac{f(P')-f(P)}{|PP'|}} \\=&\lim_{P'\to{P_0}} \left(f_x(P_0)\cos{\alpha}+f_y(P_0)\cos{\beta}+f_z(P_0)\cos{\gamma}+\frac{o(|PP'|)}{|PP'|} \right) \\=&f_x(P_0)\cos{\alpha}+f_y(P_0)\cos{\beta}+f_z(P_0)\cos{\gamma} \end{aligned} ∂l∂f===P′→P0lim∣PP′∣f(P′)−f(P)P′→P0lim(fx(P0)cosα+fy(P0)cosβ+fz(P0)cosγ+∣PP′∣o(∣PP′∣))fx(P0)cosα+fy(P0)cosβ+fz(P0)cosγ
-
相关文章:

AM@方向导数概念和定理
文章目录 abstract方向导数二元函数方向导数偏导数是方向导数的特例偏导数存在一定有对应的方向导数存在方向导数存在不一定有偏导数存在例 三元函数方向导数例 方向导数存在定理和计算公式证明二元函数三元函数 abstract 方向导数的概念,定理和计算公式方向导数是对偏导的补充…...
微信小程序隐私政策不合规,应当由用户自主阅读后自行选择是否同意隐私政策协议,不得默认强制用户同意
小程序隐私政策不合规,默认自动同意《用户服务协议》及《隐私政策》,应当由用户自主阅读后自行选择是否同意隐私政策协议,不得默认强制用户同意,请整改后再重新提交。 把 登录代表同意《用户协议》和《隐私政策》 改为 同意《用…...

Python中如何判断两个对象的内存地址是否一致?
目录 一、引言 二、Python的内存管理 三、对象的比较 四、使用id函数判断内存地址 五、总结 一、引言 在Python中,我们经常需要比较两个对象是否是同一个对象,或者说它们是否在内存中占据同一位置。在理解这个问题之前,我们需要了解Pyt…...
唯美仙侠3D手游2023【仙变3】画面精美/linux服务端+双端+GM后台+运营后台+详细教程
搭建资源下载地址:https://www.ldmzy.com/6618/6618.html...

React组件通信:如何优雅地实现组件间的数据传递
在React应用中,组件通信是至关重要的一部分。通过合适的数据传递和交互方式,我们可以构建出更加灵活和高效的前端应用。本文将介绍React组件通信的各种方式,并提供代码实现,帮助你更好地理解和应用这些技术。 1. 使用props进行父子…...
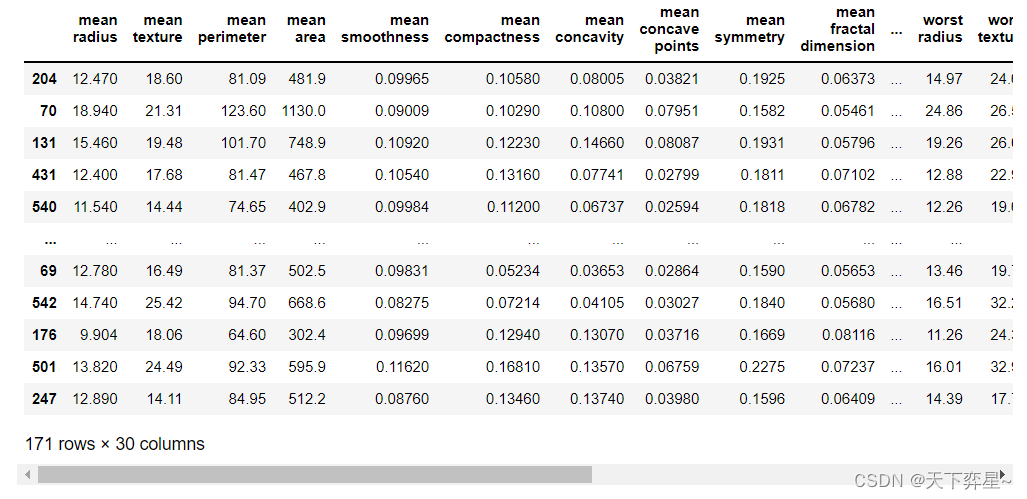
数据分析实战 | 逻辑回归——病例自动诊断分析
目录 一、数据及分析对象 二、目的及分析任务 三、方法及工具 四、数据读入 五、数据理解 六、数据准备 七、模型训练 八、模型评价 九、模型调参 十、模型预测 一、数据及分析对象 CSV文件——“bc_data.csv” 数据集链接:https://download.csdn.net/d…...
;这两行代码有什么区别?)
Eigen::Matrix<double,3,1> F;Eigen::MatrixXd F (3, 2);这两行代码有什么区别?
这两行代码的区别在于定义的矩阵 F 的类型和维度不同。 第一行: Eigen::Matrix<double,3,1> F;这行代码创建了一个3x1的矩阵 F,其中元素类型为 double。这是一个静态大小的矩阵,其维度在编译时确定。 第二行: Eigen::Ma…...

Java Agent - 应用程序代理-笔记
Java Agent - 应用程序代理-笔记 概述说明 Java Agent 又叫做 Java 探针,该功能是 Java 虚拟机提供的一整套后门,通过这套后门可以对虚拟机方方面面进行监控与分析,甚至干预虚拟机的运行。 是在 JDK1.5 引入的一种可以动态修改 Java 字节码…...

gird 卡片布局
场景一:单元格大小相等 这承载了所有 CSS Grid 中最著名的片段,也是有史以来最伟大的 CSS 技巧之一: 等宽网格响应式卡片实现 .section-content {display: grid;grid-template-columns: repeat(auto-fit, minmax(220px, 1fr));gap: 10px; …...
C#医学检验室(LIS)信息管理系统源码
LIS:实验室信息管理系统 (Laboratory Information Management System简称:LIS)。 LIS 是面向医院检验科、检验中心、动物实验所、生物医疗研究所等科研单位研发的集数据采集、传输、存储、分析、处理、发布等功能于一体的信息管理系统。 一、完善的质控: 从样本管理…...

建行广东江门分行:科技赋能,数据助力纠“四风”
为进一步深化落实中央八项规定精神,持续加大“四风”问题查处力度,建行驻江门市分行纪检组根据《广东省分行贯彻落实中央八项规定精神持之以恒纠治“四风”实施方案》(建粤党发〔2023〕1号)安排,对驻在市分行开展“四风…...
》)
3164:练27.1 叮叮当当 《信息学奥赛一本通编程启蒙(C++版)》
3164:练27.1 叮叮当当 《信息学奥赛一本通编程启蒙(C版)》 【题目描述】 松鼠老师和尼克玩报数游戏。松鼠老师数到2的倍数时,尼克就说“叮叮”;松鼠老师数到3的倍数时,尼克就说“当当”;松鼠老…...
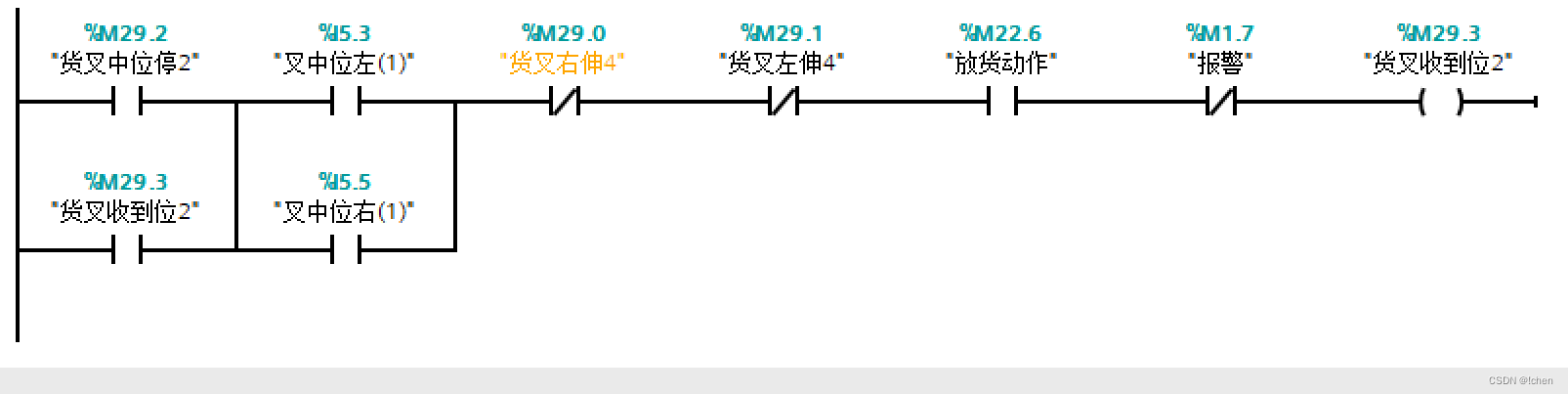
立体库堆垛机放货动作控制程序功能
放货动作程序功能块 DB11.DBX0.0 为左出货台有货 DB11.DBX1.0 为右出货台有货 左出货台车就位 DB11.DBX0.2 右出货台车就位 DB11.DBX1.2 左出货台车就位 DB11.DBX0.2 右出货台车就位 DB11.DBX1.2 左出货台车就位 DB11.DBX0.2 右出货台车就位 DB11.DBX1.2...

MySQL数据库干货_22——MySQL的用户管理
MySQL的用户管理 MySQL 是一个多用户的数据库系统,按权限,用户可以分为两种: root 用户,超级管理员,和由 root 用户创建的普通用户。 用户管理 创建用户 CREATE USER username IDENTIFIED BY password;查看用户 S…...
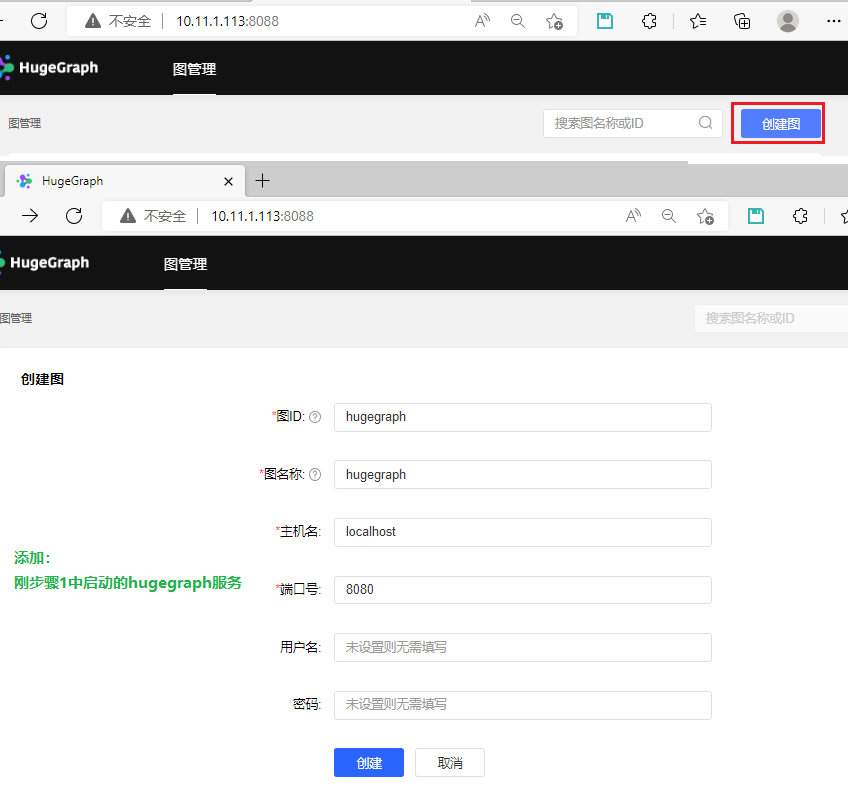
基于ubuntu 22, jdk 8x64搭建图数据库环境 hugegraph--google镜像chatgpt
基于ubuntu 22, jdk 8x64搭建图数据库环境 hugegraph download 环境 uname -a #Linux whiltez 5.15.0-46-generic #49-Ubuntu SMP Thu Aug 4 18:03:25 UTC 2022 x86_64 x86_64 x86_64 GNU/Linuxwhich javac #/adoptopen-jdk8u332-b09/bin/javac which java #/adoptopen-jdk8u33…...

4. 深度学习——优化函数
机器学习面试题汇总与解析——优化函数 本章讲解知识点 什么是优化函数?为什么要使用优化函数?详细讲解优化函数优化函数总结梯度下降算法的 batch size 总结本专栏适合于Python已经入门的学生或人士,有一定的编程基础。本专栏适合于算法工程师、机器学习、图像处理求职的学…...
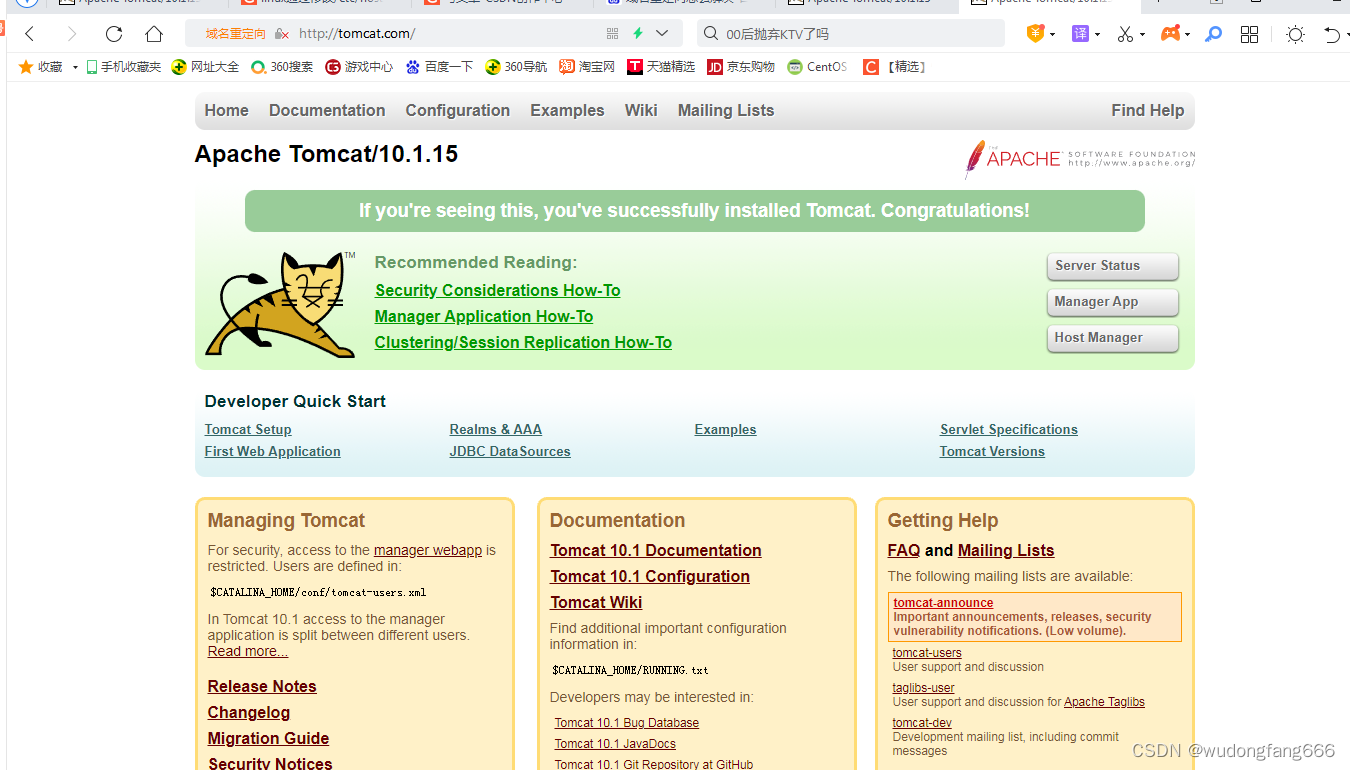
docker通过nginx代理tomcat-域名重定向
通过昨天的调试,今天做这个域名就简单了, 正常我们访问网站一般都是通过域名比如,www.baidu.com对吧,有人也通过ip,那么这个怎么做呢?物理机windows可以通过域名访问虚拟机linux的nginx代理转向tomcat服务…...

CSS BFC是什么,应用实例
CSS BFC(块级格式化上下文)是一个Web页面渲染时生成的一种独立的渲染区域,它定义了一套渲染规则,用于控制块级盒子的布局和浮动元素与其他元素的交互。BFC可以避免出现一些常见的布局问题,提高页面的可靠性和可维护性。…...

一分钟秒懂人工智能对齐
文章目录 1.什么是人工智能对齐2.为什么要研究人工智能对齐3.人工智能对齐的常见方法 1.什么是人工智能对齐 人工智能对齐(AI Alignment)指让人工智能的行为符合人的意图和价值观。 人工智能系统可能会出现“不对齐”(misalign)的…...
Postman常见报错与解决方法,持续更新~
postman中文文档 基本操作:从控制台查看请求报错 如果 Postman 无法发送你的请求,或者如果它没有收到你发送请求的 API 的响应,你将收到一条错误消息。此消息将包含问题概述和指向控制台的链接,你可以在其中访问有关请求的详细信…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
