通过拉普拉斯特征映射降维
拉普拉斯特征映射(Laplacian Eigenmaps),主要包括拉普拉斯特征映射(Laplacian Eigenmaps)使用实例、应用技巧、基本知识点总结和需要注意事项,具有一定的参考价值,需要的朋友可以参考一下。
1 介绍
拉普拉斯特征映射(Laplacian Eigenmaps)是一种不太常见的降维算法,它看问题的角度和常见的降维算法不太相同,是从局部的角度去构建数据之间的关系。也许这样讲有些抽象,具体来讲,拉普拉斯特征映射是一种基于图的降维算法,它希望相互间有关系的点(在图中相连的点)在降维后的空间中尽可能的靠近,从而在降维后仍能保持原有的数据结构。
2 推导
拉普拉斯特征映射通过构建邻接矩阵为 W W W (邻接矩阵定义见这里) 的图来重构数据流形的局部结构特征。其主要思想是,如果两个数据 实例 i i i 和 j j j 很相似,那么 i i i 和 j j j 在 降维后目标子空间中应该尽量接近。设数据实例的数目为 n n n ,目标子空间即最终的降维目标的维度为 m m m 。 定义 $ n \times m$ 大小的矩阵 Y Y Y ,其中每一个行向量 y i T y_{i}^{T} yiT 是数据实例 i i i 在目标 m m m 维子空间中的向量表示(即降维后的数据实例 i i i )。我们的目的是 让相似的数据样例 i i i 和 j j j 在降维后的目标子空间里仍旧尽量接近,故拉普拉斯特征映射优化的目标函数如下:
min ∑ i , j ∥ y i − y j ∥ 2 W i j \min \sum\limits _{i, j}\left\|y_{i}-y_{j}\right\|^{2} W_{i j} mini,j∑∥yi−yj∥2Wij
下面开始推导:
$ \begin{array}{l} \sum\limits_{i=1}^{n} \sum\limits_{j=1}{n}&\left|y_{i}-y_{j}\right|{2} W_{i j} \ &=\sum\limits_{i=1}^{n} \sum\limits_{j=1}{n}\left(y_{i}{T} y_{i}-2 y_{i}^{T} y_{j}+y_{j}^{T} y_{j}\right) W_{i j} \ &=\sum\limits_{i=1}{n}\left(\sum\limits_{j=1}{n} W_{i j}\right) y_{i}^{T} y_{i}+\sum\limits_{j=1}{n}\left(\sum\limits_{i=1}{n} W_{i j}\right) y_{j}^{T} y_{j}-2 \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} y_{i}^{T} y_{j} W_{i j} \ &=2 \sum\limits_{i=1}^{n} D_{i i} y_{i}^{T} y_{i}-2 \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} y_{i}^{T} y_{j} W_{i j} \ &=2 \sum\limits_{i=1}^{n}\left(\sqrt{D_{i i}} y_{i}\right)^{T}\left(\sqrt{D_{i i}} y_{i}\right)-2 \sum\limits_{i=1}^{n} y_{i}{T}\left(\sum\limits_{j=1}{n} y_{j} W i j\right) \ &=2 \operatorname{trace}\left(Y^{T} D Y\right)-2 \sum\limits_{i=1}^{n} y_{i}^{T}(Y W)_{i} \ &=2 \operatorname{trace}\left(Y^{T} D Y\right)-2 \operatorname{trace}\left(Y^{T} W Y\right) \ &=2 \operatorname{trace}\left[Y^{T}(D-W) Y\right] \ &=2 \operatorname{trace}\left(Y^{T} L Y\right) \end{array} $
其中 $W $ 是图的邻接矩阵,对角矩阵 D D D 是图的度矩阵 ( D i i = ∑ j = 1 n W i j ) \left(D_{i i}=\sum\limits_{j=1}^{n} W_{i j}\right) (Dii=j=1∑nWij) ,$ L=D-W$ 成为图的拉普拉斯矩阵。
变换后的拉普拉斯特征映射优化的目标函数如下:
min trace ( Y T L Y ) s.t. Y T D Y = I \begin{array}{l}\min \operatorname{trace}\left(Y^{T} L Y\right)\\ \text { s.t. } Y^{T} D Y=I \end{array} mintrace(YTLY) s.t. YTDY=I
其中限制条件 s . t . Y T D Y = I s . t . Y^{T} D Y=I s.t.YTDY=I 保证优化问题有解,下面用拉格朗日乘子法对目标函数求解:
f ( Y ) = tr ( Y T L Y ) + tr [ Λ ( Y T D Y − I ) ] f(Y)=\operatorname{tr}\left(Y^{T} L Y\right)+\operatorname{tr}\left[\Lambda\left(Y^{T} D Y-I\right)\right] f(Y)=tr(YTLY)+tr[Λ(YTDY−I)]
∂ f ( Y ) ∂ Y = L Y + L T Y + D T Y Λ T + D Y Λ = 2 L Y + 2 D Y Λ = 0 \begin{array}{l} \frac{\partial f(Y)}{\partial Y}&=L Y+L^{T} Y+D^{T} Y \Lambda^{T}+D Y \Lambda \\ &=2 L Y+2 D Y \Lambda=0 \end{array} ∂Y∂f(Y)=LY+LTY+DTYΛT+DYΛ=2LY+2DYΛ=0
∴ L Y = − D Y Λ \therefore L Y=-D Y \Lambda ∴LY=−DYΛ
其中用到了矩阵的迹的求导,具体方法见 迹求导。 Λ \Lambda Λ 为一个对角矩阵,另外 L L L 、 D D D 均为实对称矩阵,其转置与自身相等。对于单独的 y y y 向量,上式可写为: L y = λ D y L y=\lambda D y Ly=λDy,这是一个广义特征值问题。通过求得 m m m 个最小非零特征值所对应的特征向量,即可达到降维的目 的。
关于这里为什么要选择 m m m 个最小非零特征值所对应的特征向量。将 $L Y=-D Y \Lambda $ 带回到 min trace ( Y T L Y ) \min \operatorname{trace}\left(Y^{T} L Y\right) mintrace(YTLY) 中,由于有着约束条件 Y T D Y = I Y^{T} D Y=I YTDY=I 的限制,可以得到 $ \min \quad \operatorname{trace}\left(Y^{T} L Y\right)=\min \quad t r a c e(-\Lambda)$ 。即为特 征值之和。我们为了目标函数最小化,要选择最小的 m m m 个特征值所对应的特征向量。
3 步骤
使用时算法具体步骤为:
步骤1:构建图
使用某一种方法来将所有的点构建成一个图,例如使用KNN算法,将每个点最近的K个点连上边。K是一个预先设定的值。
步骤2:确定权重
确定点与点之间的权重大小,例如选用热核函数来确定,如果点 i 和点 j 相连,那么它们关系的权重设定为:
W i j = e − ∥ x i − x j ∥ 2 t W_{i j}=e^{-\frac{\left\|x_{i}-x_{j}\right\|^{2}}{t}} Wij=e−t∥xi−xj∥2
另外一种可选的简化设定是 W i j = 1 W_{i j}=1 Wij=1 如果点 i i i ,$ j$ 相连,否则 $W_{i j}=0 $ 。
步骤3:特征映射
计算拉普拉斯矩阵 L L L 的特征向量与特征值: $L y=\lambda D y $
使用最小的 m m m 个非零特征值对应的特征向量作为降维后的结果输出。
相关文章:

通过拉普拉斯特征映射降维
拉普拉斯特征映射(Laplacian Eigenmaps),主要包括拉普拉斯特征映射(Laplacian Eigenmaps)使用实例、应用技巧、基本知识点总结和需要注意事项,具有一定的参考价值,需要的朋友可以参考一下。 1 …...
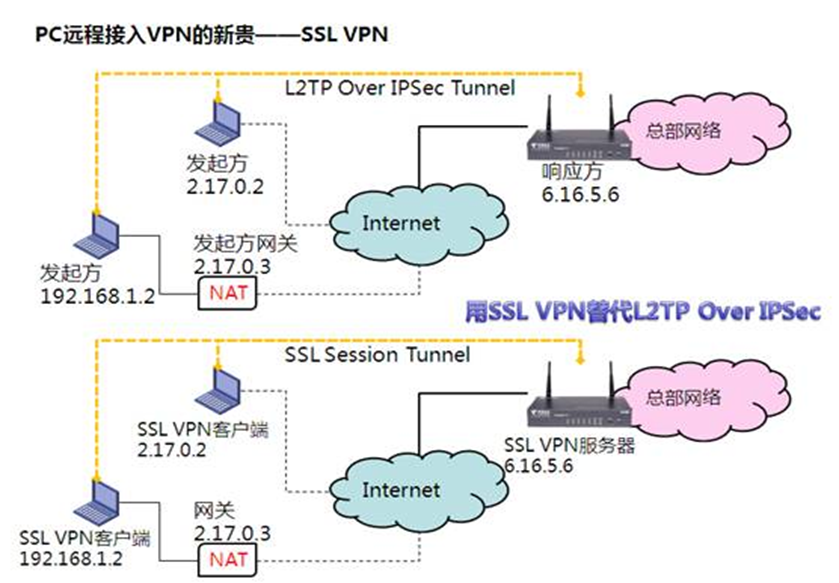
【信息安全原理】——传输层安全(学习笔记)
📖 前言:为保证网络应用,特别是应用广泛的Web应用数据传输的安全性(机密性、完整性和真实性),可以在多个网络层次上采取安全措施。本篇主要介绍传输层提供应用数据安全传输服务的协议,包括&…...

GBDT减少模型偏差、随机森林减小模型方差
1、Adaboost算法原理,优缺点: 理论上任何学习器都可以用于Adaboost.但一般来说,使用最广泛的Adaboost弱学习器是决策树和神经网络。对于决策树,Adaboost分类用了CART分类树,而Adaboost回归用了CART回归树。 Adaboost…...

使用IDEA工具处理git合并后的冲突的细节
使用 IDEA 处理合并(merge) 使用IDEA处理git合并如果遇到冲突,对冲突文件的不冲突部分需要处理吗?会自动将双方不冲突的部分合并吗? 比如如下,使用 IDEA 合并 branch1 到 branch2 分支,出现了冲突,如下图…...

快速下载ChatGLM系列模型
1. 说明与步骤 在无法访问huggingface的网络环境下(或者是网速不够好时),(目前)还可以使用参考1中清华云盘的链接来下载,在linux下可以直接用如下wget命令来下载最耗时的模型部分。注意还需要把模型的.py等…...
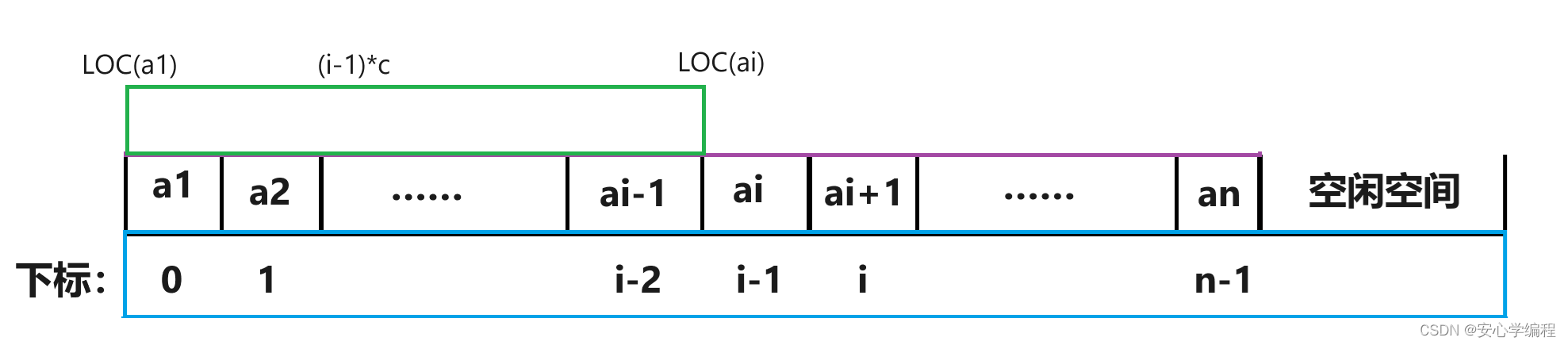
【数据结构】顺序表 | 详细讲解
在计算机中主要有两种基本的存储结构用于存放线性表:顺序存储结构和链式存储结构。本篇文章介绍采用顺序存储的结构实现线性表的存储。 顺序存储定义 线性表的顺序存储结构,指的是一段地址连续的存储单元依次存储链性表的数据元素。 线性表的…...
——第1天:什么是风控建模?)
100天精通风控建模(原理+Python实现)——第1天:什么是风控建模?
风控模型已在各大银行和公司都实际运用于业务,用于营销和风险控制等。本文以视频的形式阐述什么是风控建模,并提供风控建模原理和Python实现文章清单。首先了解什么是风控建模? 下文梳理风控模型搭建的原理和Python实现,按顺序做成清单的形式,点击即可进入相应文章链接。方…...

HTML转义字符
HTML,XML文件中存在部分字符作为标志字符无法作为文本内容使用,如< >,如果想在文本中输出,可使用转义字符。 < 的转义字符为 " < " > 的转义字符为 " > " <TextView.... ....android:t…...

【STM32】
STM32 1 CMSIS1.1 概述1.2 CMSIS 应用程序文件描述 2 库2.1 简介2.2 标准外设库(standrd Peripheral Libraries)2.3 HAL 库2.3.1 目录结构2.3.2 HAL库API函数和变量的命名规则2.3.3 HAL库对寄存器位操作的相关宏定义2.3.4 HAL库回调函数2.3.5 HAL使用注意…...
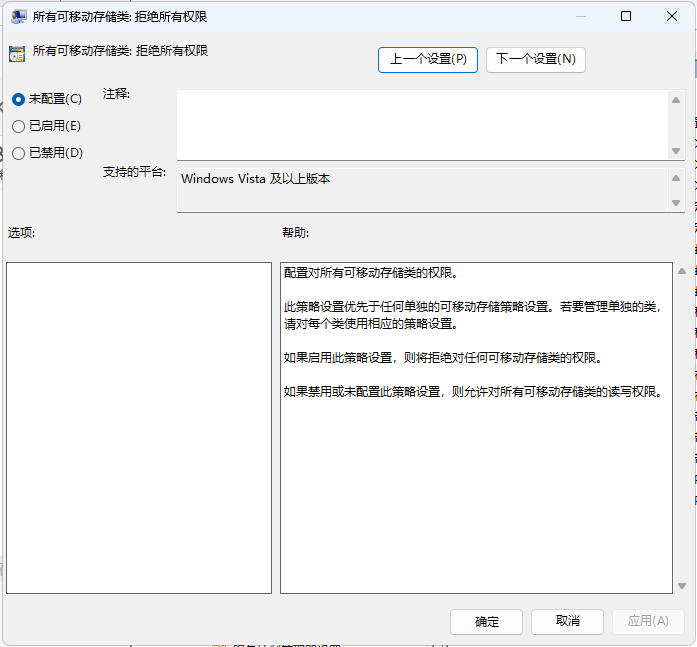
U盘不可以访问的维护
u盘打不开,可按下图,设置:winR→gpedit.msc;配置“管理模板”→“系统”→“可移动存储访问”→“所有可移动存储类”。 然后,选择“未配置”,如下图...
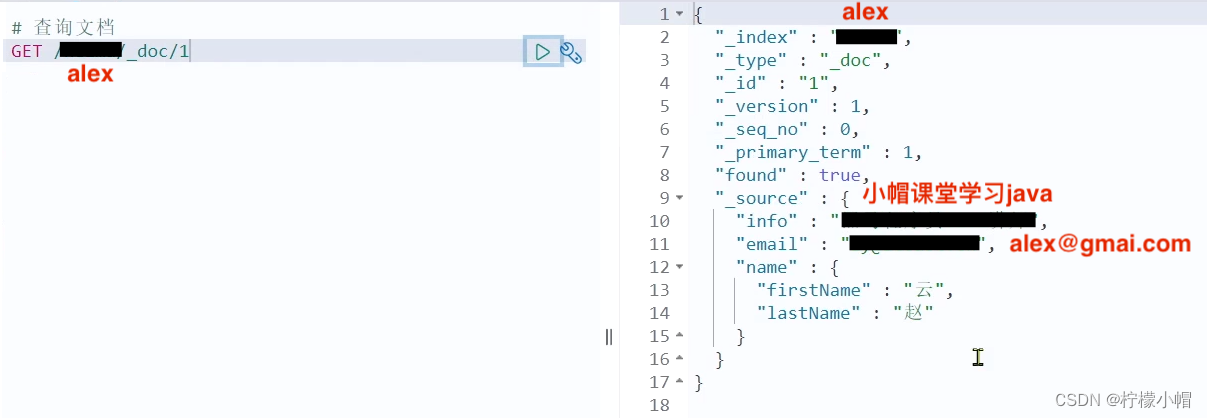
SpringCloud 微服务全栈体系(十三)
第十一章 分布式搜索引擎 elasticsearch 二、索引库操作 索引库就类似数据库表,mapping 映射就类似表的结构。 我们要向 es 中存储数据,必须先创建“库”和“表”。 1. mapping 映射属性 mapping 是对索引库中文档的约束,常见的 mapping …...

ROC 曲线详解
前言 ROC 曲线是一种坐标图式的分析工具,是由二战中的电子和雷达工程师发明的,发明之初是用来侦测敌军飞机、船舰,后来被应用于医学、生物学、犯罪心理学。 如今,ROC 曲线已经被广泛应用于机器学习领域的模型评估,说…...

113.路径总和II
原题链接:113.路径总和II 需复刷 思路: 跟112.路径总和不同,该题是要你找出所有相同的路径,那么此时就要注意存储,递归和回溯了。 全代码: class Solution { public:vector<vector<int>> re…...

【Linux】WSL安装Kali及基本操作
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍WSL安装Kali及基本操作。 学其所用,用其所学。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下次更新不迷路…...
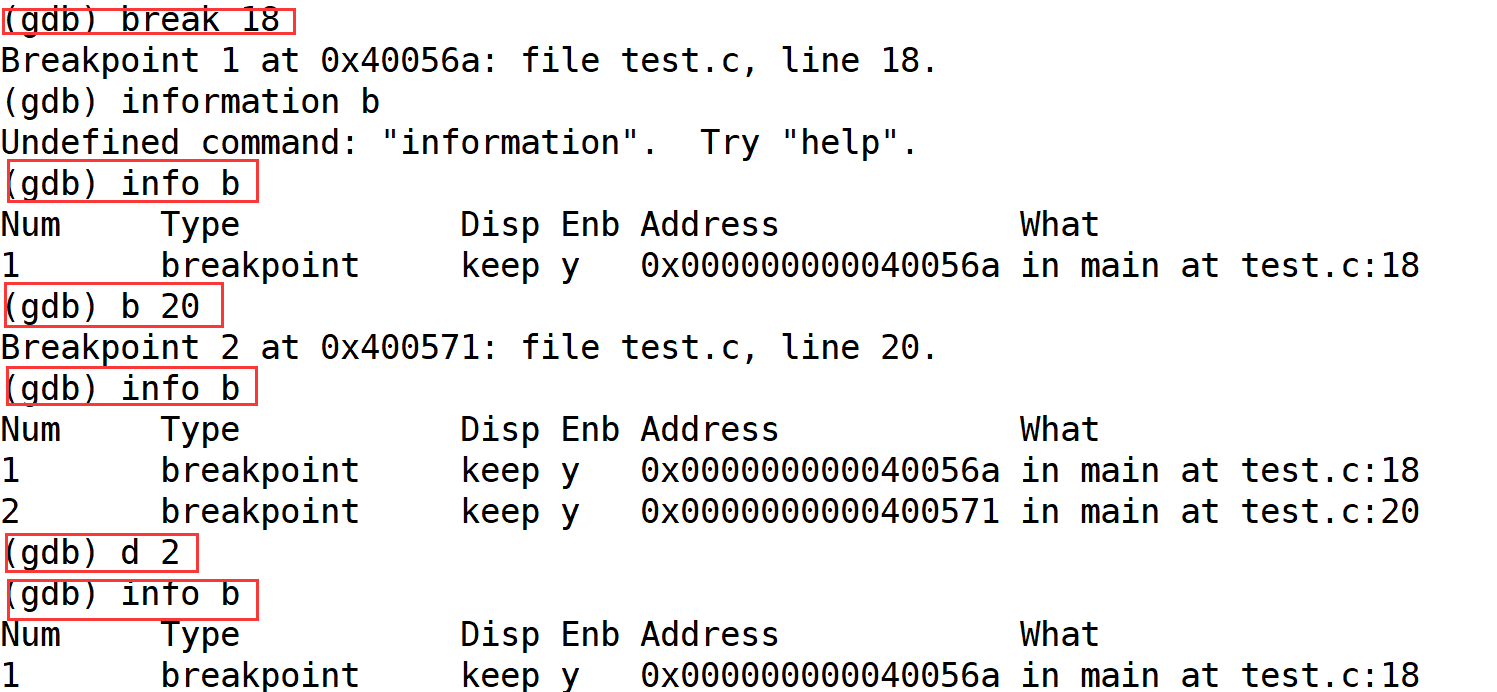
Linux基础开发工具之调试器gdb
文章目录 1.编译成的可调试的debug版本1.1gcc test.c -o testdebug -g1.2readelf -S testdebug | grep -i debug 2.调试指令2.0quit退出2.1list/l/l 数字: 显示代码2.2run/r运行2.3断点相关1. break num/b num: 设置2. info b: 查看3. d index: 删除4. n: F10逐过程5. p 变量名…...
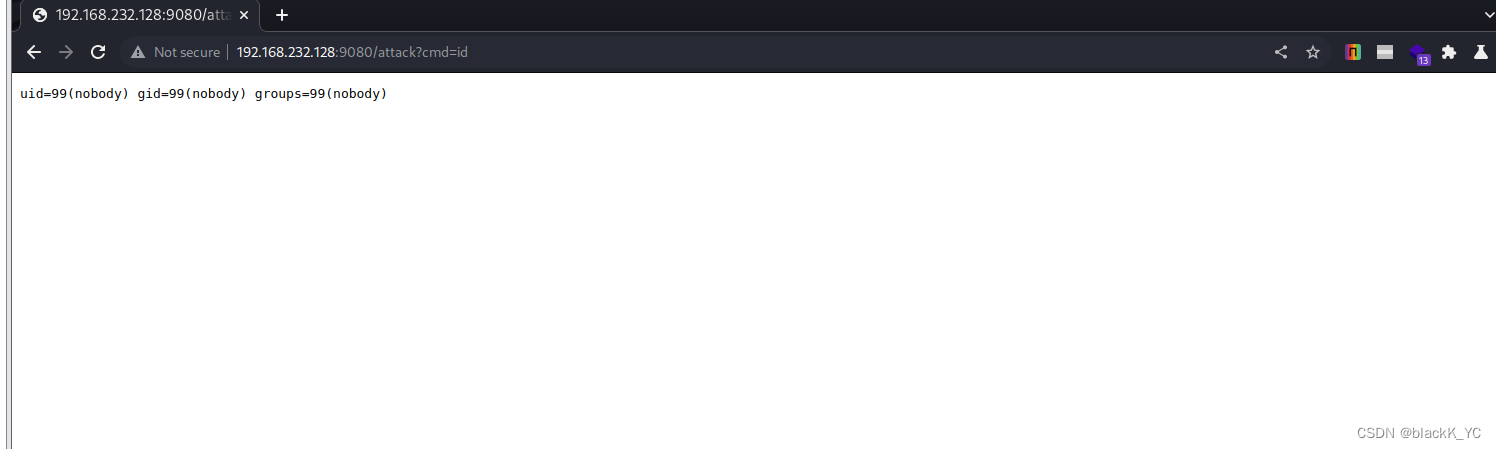
Apache APISIX 的 Admin API 默认访问令牌漏洞(CVE-2020-13945)漏洞复现
漏洞描述 Apache APISIX 是一个动态、实时、高性能的 API 网关。Apache APISIX 有一个默认的内置 API 令牌,可用于访问所有 admin API,通过 2.x 版本中添加的参数导致远程执行 LUA 代码。 漏洞环境及利用 启动docker环境 访问9080端口 通过 admin api…...
Clickhouse学习笔记(3)—— Clickhouse表引擎
前言: 有关Clickhouse的前置知识详见: 1.ClickHouse的安装启动_clickhouse后台启动_THE WHY的博客-CSDN博客 2.ClickHouse目录结构_clickhouse 目录结构-CSDN博客 Cickhouse创建表时必须指定表引擎 表引擎(即表的类型)决定了&…...

WebSocket是什么以及其与HTTP的区别
新钛云服已累计为您分享774篇技术干货 HTTP协议 HTTP是单向的,客户端发送请求,服务器发送响应。举个例子,当用户向服务器发送请求时,该请求采用HTTP或HTTPS的形式,在接收到请求后,服务器将响应发送给客户端…...

Flutter 实战:构建跨平台应用
文章目录 一、简介二、开发环境搭建三、实战案例:开发一个简单的天气应用1. 项目创建2. 界面设计3. 数据获取4. 实现数据获取和处理5. 界面展示6. 添加动态效果和交互7. 添加网络错误处理8. 添加刷新功能9. 添加定位功能10. 添加通知功能11. 添加数据持久化功能 《F…...

Python中68个内置函数的使用与归类
前言 在Python解释器中内置的、可以直接使用的函数。这些函数不需要额外的导入或安装,可以直接在Python代码中调用。Python内置函数包括了很多常用的功能,比如对数据类型的操作、数学运算、字符串处理、文件操作等。一些常见的内置函数包括print()、len…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
