（一）正点原子I.MX6ULL kernel6.1移植
一、概述
学完了正点原子的I.MX6ULL移植，正点原子的教程是基于Ubuntu18，使用的是4.1.15的内核，很多年前的了。NXP官方也发布了新的6.1的内核，以及2022.04的uboot。
本文分享一下基于Ubuntu22.04（6.2.0-36-generic）I.MX6ULL的uboot（v2022.04）和kernel（6.1.y）的移植。
新版uboot移植最大不同就是使用了设备树，相对正点原子之前的教程要简单很多
二、官方Uboot和Kernel下载
这里我们可以去NXP的github里找：https://github.com/nxp-imx/，如果打不开的话可以直接使用笔者提供的SSH链接：
SSH：
Linux：git@github.com:nxp-imx/linux-imx.git
Uboot：git@github.com:nxp-imx/uboot-imx.git
HTTPS：
Linux：https://github.com/nxp-imx/linux-imx.git
Uboot：GitHub - nxp-imx/uboot-imx: i.MX U-Boot
在分支里找到最新版本，截止到2023年11月12日，最新是6.1的内核
三、交叉编译器
笔者使用的是Linaro GCC编译器
Linaro GCC：https://releases.linaro.org/components/toolchain/binaries/latest-7/arm-linux-gnueabihf/
这里选择gcc-linaro-7.5.0-2019.12-x86_64_arm-linux-gnueabihf.tar.xz
x86_64是电脑架构x86（64位）
找一个文件夹，把压缩包解压出来，然后打开/etc/profile，在最后面添加：
export PATH=$PATH:(交叉编译器目录)/bin
然后重启。
详细的交叉编译器安装可以参考正点原子的教程或者:
http://t.csdnimg.cn/S2TYd
相关文章：
（一）正点原子I.MX6ULL kernel6.1移植
一、概述 学完了正点原子的I.MX6ULL移植，正点原子的教程是基于Ubuntu18，使用的是4.1.15的内核，很多年前的了。NXP官方也发布了新的6.1的内核，以及2022.04的uboot。 本文分享一下基于Ubuntu22.04（6.2.0-36-generic&…...
计算机服务器中了mallox勒索病毒怎么解决，勒索病毒解密，数据恢复
企业的计算机服务器为企业的数据存储提供了极大便利，也让企业的生产运行效率得到了极大提升，但是网络数据安全威胁随着技术的不断发展也不断增加。近期，云天数据恢复中心接到很多企业的求助，企业的计算机服务器遭到了mallox勒索病…...
CSS3实现动态旋转加载样式
要使用 CSS3 创建一个动态旋转加载样式，可以使用 CSS 动画和旋转变换。下面是一个简单的示例： HTML： <div class"loader"></div> CSS： .loader {width: 50px;height: 50px;border: 4px solid #3498db;b…...
【LeetCode刷题-二分查找】--658.找到K个最接近的元素
658.找到K个最接近的元素 方法一：二分查找双指针 假设数组长度为n，数组arr已经按照升序排序，可以将数组arr分为两部分，前一部分所有元素[0,left]都小于x，后一部分[right,n-1]都大于等于x，left与right都可以…...
新方向！文心一言X具身智能，用LLM大模型驱动智能小车
具身智能已成为近年来研究的热点领域之一。具身智能强调将智能体与实体环境相结合，通过智能体与环境的交互，来感知和理解世界，最终实现在真实环境中的自主决策和运动控制。 如何基于文心大模型，低成本入门“具身智能”࿰…...
mysql.sock找不到怎么解决？
当我们连接mysql时找不到mysql.sock的时候会出现下列情况： cant connect to mysql server through socket /tmp/mysql.sock 解决方法： （1）找到mysql.sock 使用 find / -name mysql.sock 进行寻找。 如果找不到，那…...
微信小程序刷新当前页面（亲测有效）
有个小功能点，需要刷新当前页面，搜索了很多地方，发现很多搜索的结果其实并不准确。 有的调用的是this.onLoad方法，有的是调用的是this.onReady方法。其实都不能满足我的要求，其实我就只是想刷新下当前页面，…...
通过拉普拉斯特征映射降维
拉普拉斯特征映射（Laplacian Eigenmaps），主要包括拉普拉斯特征映射（Laplacian Eigenmaps）使用实例、应用技巧、基本知识点总结和需要注意事项，具有一定的参考价值，需要的朋友可以参考一下。 1 …...
【信息安全原理】——传输层安全（学习笔记）
📖 前言：为保证网络应用，特别是应用广泛的Web应用数据传输的安全性（机密性、完整性和真实性），可以在多个网络层次上采取安全措施。本篇主要介绍传输层提供应用数据安全传输服务的协议，包括&…...
GBDT减少模型偏差、随机森林减小模型方差
1、Adaboost算法原理，优缺点： 理论上任何学习器都可以用于Adaboost.但一般来说，使用最广泛的Adaboost弱学习器是决策树和神经网络。对于决策树，Adaboost分类用了CART分类树，而Adaboost回归用了CART回归树。 Adaboost…...
使用IDEA工具处理git合并后的冲突的细节
使用 IDEA 处理合并(merge) 使用IDEA处理git合并如果遇到冲突，对冲突文件的不冲突部分需要处理吗？会自动将双方不冲突的部分合并吗？ 比如如下，使用 IDEA 合并 branch1 到 branch2 分支，出现了冲突，如下图…...
快速下载ChatGLM系列模型
1. 说明与步骤 在无法访问huggingface的网络环境下（或者是网速不够好时），（目前）还可以使用参考1中清华云盘的链接来下载，在linux下可以直接用如下wget命令来下载最耗时的模型部分。注意还需要把模型的.py等…...
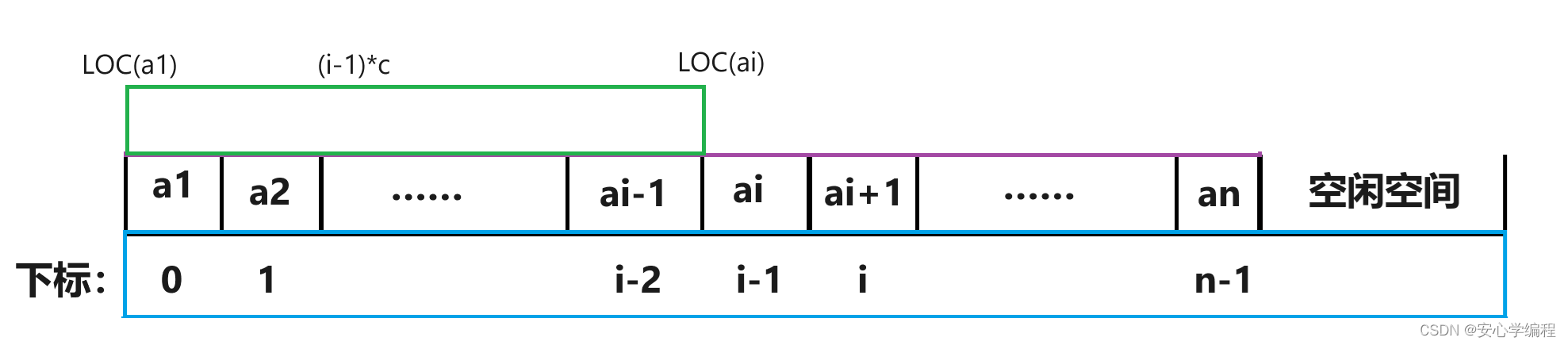
【数据结构】顺序表 | 详细讲解
在计算机中主要有两种基本的存储结构用于存放线性表：顺序存储结构和链式存储结构。本篇文章介绍采用顺序存储的结构实现线性表的存储。 顺序存储定义 线性表的顺序存储结构，指的是一段地址连续的存储单元依次存储链性表的数据元素。 线性表的…...
——第1天：什么是风控建模？)
100天精通风控建模(原理+Python实现)——第1天：什么是风控建模？
风控模型已在各大银行和公司都实际运用于业务，用于营销和风险控制等。本文以视频的形式阐述什么是风控建模，并提供风控建模原理和Python实现文章清单。首先了解什么是风控建模？ 下文梳理风控模型搭建的原理和Python实现，按顺序做成清单的形式，点击即可进入相应文章链接。方…...
HTML转义字符
HTML，XML文件中存在部分字符作为标志字符无法作为文本内容使用，如< >，如果想在文本中输出，可使用转义字符。 < 的转义字符为 " < " > 的转义字符为 " > " <TextView.... ....android:t…...
【STM32】
STM32 1 CMSIS1.1 概述1.2 CMSIS 应用程序文件描述 2 库2.1 简介2.2 标准外设库（standrd Peripheral Libraries）2.3 HAL 库2.3.1 目录结构2.3.2 HAL库API函数和变量的命名规则2.3.3 HAL库对寄存器位操作的相关宏定义2.3.4 HAL库回调函数2.3.5 HAL使用注意…...
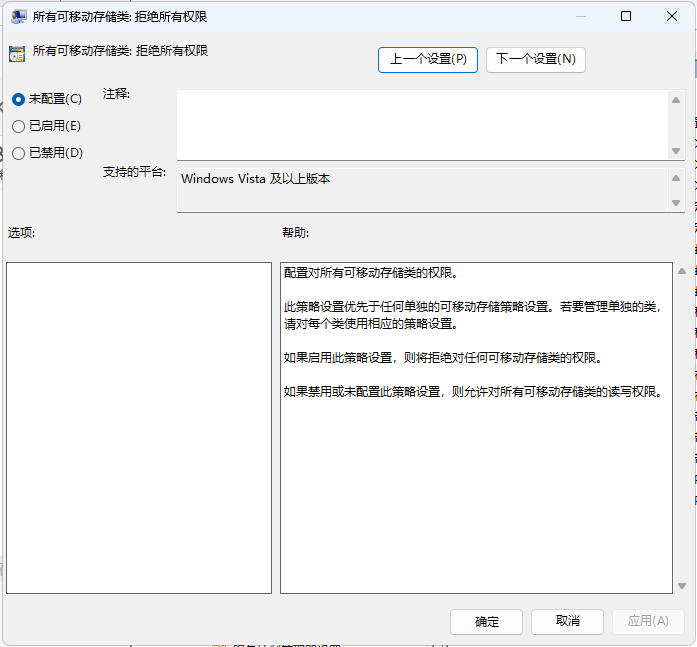
U盘不可以访问的维护
u盘打不开，可按下图，设置：winR→gpedit.msc；配置“管理模板”→“系统”→“可移动存储访问”→“所有可移动存储类”。 然后，选择“未配置”，如下图...
SpringCloud 微服务全栈体系（十三）
第十一章 分布式搜索引擎 elasticsearch 二、索引库操作 索引库就类似数据库表，mapping 映射就类似表的结构。 我们要向 es 中存储数据，必须先创建“库”和“表”。 1. mapping 映射属性 mapping 是对索引库中文档的约束，常见的 mapping …...
ROC 曲线详解
前言 ROC 曲线是一种坐标图式的分析工具，是由二战中的电子和雷达工程师发明的，发明之初是用来侦测敌军飞机、船舰，后来被应用于医学、生物学、犯罪心理学。 如今，ROC 曲线已经被广泛应用于机器学习领域的模型评估，说…...
113.路径总和II
原题链接：113.路径总和II 需复刷 思路： 跟112.路径总和不同，该题是要你找出所有相同的路径，那么此时就要注意存储，递归和回溯了。 全代码： class Solution { public:vector<vector<int>> re…...
TDengine 快速体验（Docker 镜像方式）
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能，本节首先介绍如何通过 Docker 快速体验 TDengine，然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker，请使用 安装包的方式快…...
云计算——弹性云计算器（ECS）
弹性云服务器：ECS 概述 云计算重构了ICT系统，云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台，包含如下主要概念。 ECS（Elastic Cloud Server）：即弹性云服务器，是云计算…...
《Playwright：微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络，将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具，支持 Chrome、Firefox、Safari 等主流浏览器，提供多语言 API（Python、JavaScript、Java、.NET）。它的特点包括&a…...
linux 错误码总结
1，错误码的概念与作用 在Linux系统中，错误码是系统调用或库函数在执行失败时返回的特定数值，用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递，errno由操作系统维护，保存最近一次发生的错误信息。值得注意的是，errno的值在每次系统调用或函数调用失败时…...
Caliper 配置文件解析：config.yaml
Caliper 是一个区块链性能基准测试工具，用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构，并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件，主要包含以下几个部…...
服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行！ sudo su - 1. CentOS 系统： yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT，橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版：职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具，专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑（如DBC、LDF、ARXML、HEX等），并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
高防服务器价格高原因分析
高防服务器的价格较高，主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因： 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器，因此…...
Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...