java算法学习索引之动态规划
一 斐波那契数列问题的递归和动态规划
【题目】给定整数N,返回斐波那契数列的第N项。
补充问题 1:给定整数 N,代表台阶数,一次可以跨 2个或者 1个台阶,返回有多少种走法。
【举例】N=3,可以三次都跨1个台阶;也可以先跨2个台阶,再跨1个台阶;还可以先跨1个台阶,再跨2个台阶。所以有三种走法,返回3。
补充问题 2:假设农场中成熟的母牛每年只会生 1 头小母牛,并且永远不会死。第一年农场有1只成熟的母牛,从第二年开始,母牛开始生小母牛。每只小母牛3年之后成熟又可以生小母牛。给定整数N,求出N年后牛的数量。
【举例】N=6,第1年1头成熟母牛记为a;第2年a生了新的小母牛,记为b,总牛数为2;第3年a生了新的小母牛,记为c,总牛数为3;第4年a生了新的小母牛,记为d,总牛数为4。第5年b成熟了,a和b分别生了新的小母牛,总牛数为6;第6年c也成熟了,a、b和c分别生了新的小母牛,总牛数为9,返回9。
【要求】对以上所有的问题,请实现时间复杂度为O(logN)的解法。
斐波那契数列问题

奶牛问题


private int[][] multiMatrix(int[][] m1, int[][] m2) {//矩阵乘法// TODO Auto-generated method stubint[][] res=new int[m1.length][m2[0].length];for (int i = 0; i < m1.length; i++) {for (int j = 0; j < m2[0].length; j++) {for (int k = 0; k < m2.length; k++) {res[i][j]+=m1[i][k]*m2[k][j];}}}return res;
}public int f3(int n)
{if (n<1) {return 0;}if (n==1||n==2) {return 1;}int [][] base= {{1,1},{1,0}};int[][] res=matrixPower(base, n-2);return res[0][0]+res[1][0];
}public int c3(int n)
{if (n<1) {return 0;}if (n==1||n==2||n==3) {return 3;}int [][] base= {{1,0,1},{0,0,1},{1,0,0}};int[][] res=matrixPower(base, n-3);return 3*res[0][0]+2*res[1][0]+res[2][0];
}
二 矩阵的最小路径和
给定一个矩阵 m,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,返回所有的路径中最小的路径和。
经典动态规划方法。假设矩阵 m的大小为 M×N,行数为 M,列数为 N。先生成大小和 m一样的矩阵dp,dp[i][j]的值表示从左上角(即(0,0))位置走到(i,j)位置的最小路径和。对m的第一行的所有位置来说,即(0,j)(0≤j<N),从(0,0)位置走到(0,j)位置只能向右走,所以(0,0)位置到(0,j)位置的路径和就是 m[0][0..j]这些值的累加结果。同理,对 m 的第一列的所有位置来说,即(i,0) (0≤i<M),从(0,0)位置走到(i,0)位置只能向下走,所以(0,0)位置到(i,0)位置的路径和就是m[0..i][0]这些值的累加结果。
除第一行和第一列的其他位置(i,j)外,都有左边位置(i-1,j)和上边位置(i,j-1)。从(0,0)到(i,j)的路径必然经过位置(i-1,j)或位置(i,j-1),所以,dp[i][j]=min{dp[i-1][j],dp[i][j-1]}+m[i][j],含义是比较从(0,0)位置开始,经过(i-1,j)位置最终到达(i,j)的最小路径和经过(i,j-1)位置最终到达(i,j)的最小路径之间,哪条路径的路径和更小。那么更小的路径和就是 dp[i][j]的值。
public int minPathSum1(int[][] m) {if (m==null||m.length==0||m[0]==null||m[0].length==0) {return 0;}int row=m.length;int col=m[0].length;int[][] dp=new int[row][col];dp[0][0]=m[0][0];for (int i = 1; i < row; i++) {dp[i][0]=dp[i-1][0]+m[i][0];}for (int j = 0; j < col; j++) {dp[0][j]=dp[0][j-1]+m[0][j];}for (int i = 1; i < row; i++) {for (int j = 0; j < col; j++) {dp[i][j]=Math.min(dp[i-1][j], dp[i][j-1])+m[i][j];}}return dp[row-1][col-1];}
矩阵中一共有 M×N 个位置,每个位置都计算一次从(0,0)位置达到自己的最小路径和,计算的时候只是比较上边位置的最小路径和与左边位置的最小路径和哪个更小,所以时间复杂度为O(M×N),dp矩阵的大小为M×N,所以额外空间复杂度为O(M×N)。动态规划经过空间压缩后的方法。这道题的经典动态规划方法在经过空间压缩之后,时间复杂度依然是O(M×N),但是额外空间复杂度可以从O(M×N)减小至O(min{M,N}),也就是不使用大小为M×N的dp矩阵,而仅仅使用大小为min{M,N}的arr数组。具体过程如下
public int minPathSum2(int[][] m)
{if (m==null||m.length==0||m[0]==null||m[0].length==0) {return 0;}int more=Math.max(m.length, m[0].length);int less=Math.min(m.length, m[0].length);boolean rowmore= more==m.length;int[] arr=new int[less];arr[0]=m[0][0];for (int i = 1; i < less; i++) {arr[i]=arr[i-1]+(rowmore? m[0][i]:m[i][0]);//先求出到对角线的值}//数组 arr 中保存的是dp[i][i]中的值,但如果给定的矩阵行数小于列数(M<N),那么就生成长度为M的arr,然后令arr更新成dp矩阵每一列的值,及将arr 中的值保存为 dp[i][N]// 从左向右滚动过去for (int i = 1; i < more; i++) {arr[0]=arr[0]+(rowmore?m[i][0]:m[0][i]);for (int j = 1; j < arr.length; j++) {arr[j]=Math.min(arr[j-1], arr[j])+(rowmore?m[i][j]:m[j][i]);}}return arr[less-1];}相关文章:

java算法学习索引之动态规划
一 斐波那契数列问题的递归和动态规划 【题目】给定整数N,返回斐波那契数列的第N项。 补充问题 1:给定整数 N,代表台阶数,一次可以跨 2个或者 1个台阶,返回有多少种走法。 【举例】N3,可以三次都跨1个台…...

ChatGPT重磅升级 奢侈品VERTU推出双模型AI手机
2023年11月7日,OpenAI举办了首届开发者大会,CEO Sam Altman(山姆奥尔特曼)展示了号称“史上最强”AI的GPT-4 Turbo。它支持长达约10万汉字的输入,具备前所未有的长文本处理能力,使更复杂的互动成为可能。此外,GPT-4 Turbo还引入了跨模态API支持,可以同时处理图片、视频和声音,从…...
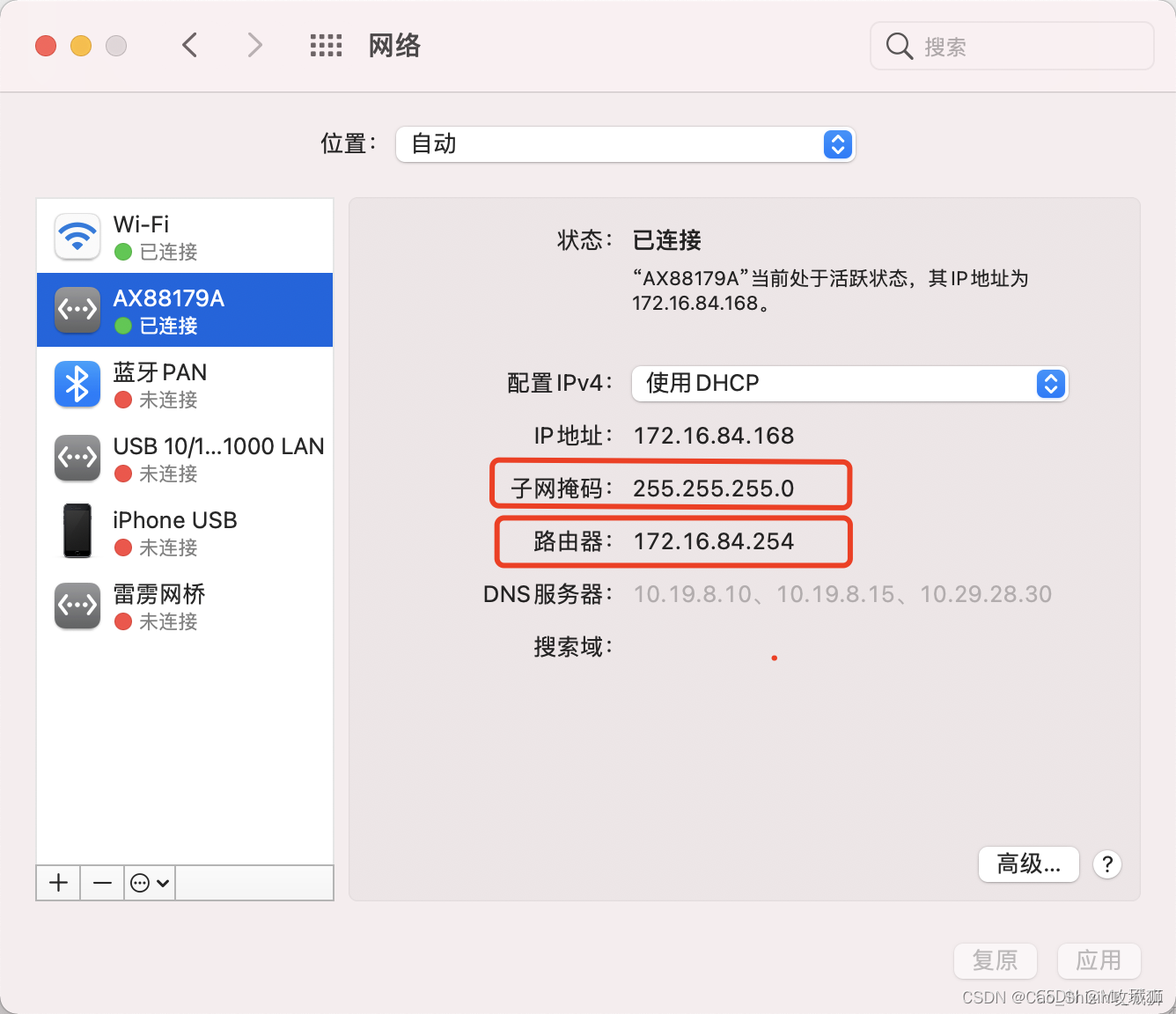
mac配置双网卡 mac同时使用内网和外网
在公司办公通常都会连内网,而连内网最大的限制就是不可以使用外网,那遇到问题也就不能google,而当连接无线的时候,内网的东西就不可以访问,也就不能正常办公,对于我这种小白来说,工作中遇到的问…...

深度探究深度学习常见数据类型INT8 FP32 FP16的区别即优缺点
定点和浮点都是数值的表示(representation),它们区别在于,将整数(integer)部分和小数(fractional)部分分开的点,点在哪里。定点保留特定位数整数和小数,而浮点…...
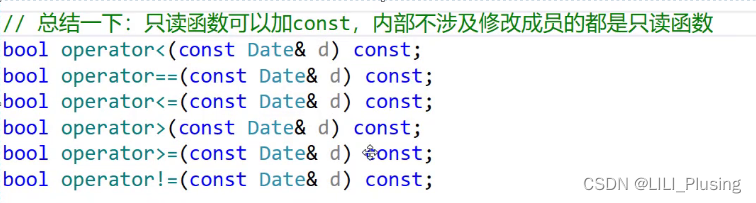
C++——const成员
这里先用队列举例: #define _CRT_SECURE_NO_WARNINGS 1 #include <iostream> #include <assert.h> using namespace std; class SeqList { public:void pushBack(int data){if (_size _capacity){int* tmp (int*)realloc(a, sizeof(int) * 4);if (tm…...
使用阿里云服务器学习Docker
首先我这里选择的系统服务器是CentOS 7.9 64位 因为centos系统里面的安装指令是:yum,而非apt-get. yum install docker -y试着建立一个容器: docker run -d -p 80:80 httpd启动docker的守护进程: sudo systemctl start docker 查看Docke…...

通信原理板块——线性分组码之汉明码
微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等 1、汉明码 (1)常见概念 代数码&…...
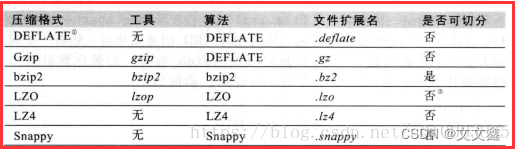
Hive 常用存储、压缩格式
1. Hive常用的存储格式 TEXTFI textfile为默认存储格式 存储方式:行存储 磁盘开销大 数据解析开销大 压缩的text文件 hive 无法进行合拆分 SEQUENCEFILE sequencefile二进制文件,以<key,value>的形式序列到文件中 存储方式:行存储 可…...

搞懂它,就可以把结构体玩活了~
正文 大家周末好,我是bug菌~ 今天主要是跟大家详细聊聊container_of这个宏定义,非常经典的宏,只是一直没有抽时间细细品味,今天就跟大家一起来看看有何神奇之处: 1 offsetof 首先我们需要简单看看offsetof(TYPE, MEMBER) 这个宏定…...
基于SpringBoot+Redis的前后端分离外卖项目-苍穹外卖(四)
编辑员工和分类模块功能开发 1. 编辑员工1.1 需求分析与设计1.1.1 产品原型1.1.2 接口设计 1.2 代码开发1.2.1 回显员工信息功能1.2.2 修改员工信息功能 1.3 功能测试 2. 分类模块功能开发2.1 需求分析与设计2.1.1 产品原型2.1.2 接口设计2.1.3 表设计 2.2 代码实现2.2.1 Mappe…...
dcat admin 各种问题
样式问题 如何根据条件给表格数据栏添加背景色 use Illuminate\Support\Collection;protected function grid(){return Grid::make(new BookArticle(), function (Grid $grid) {... 其他代码// Collection的完整路径:Illuminate\Support\Collection;$grid->row…...
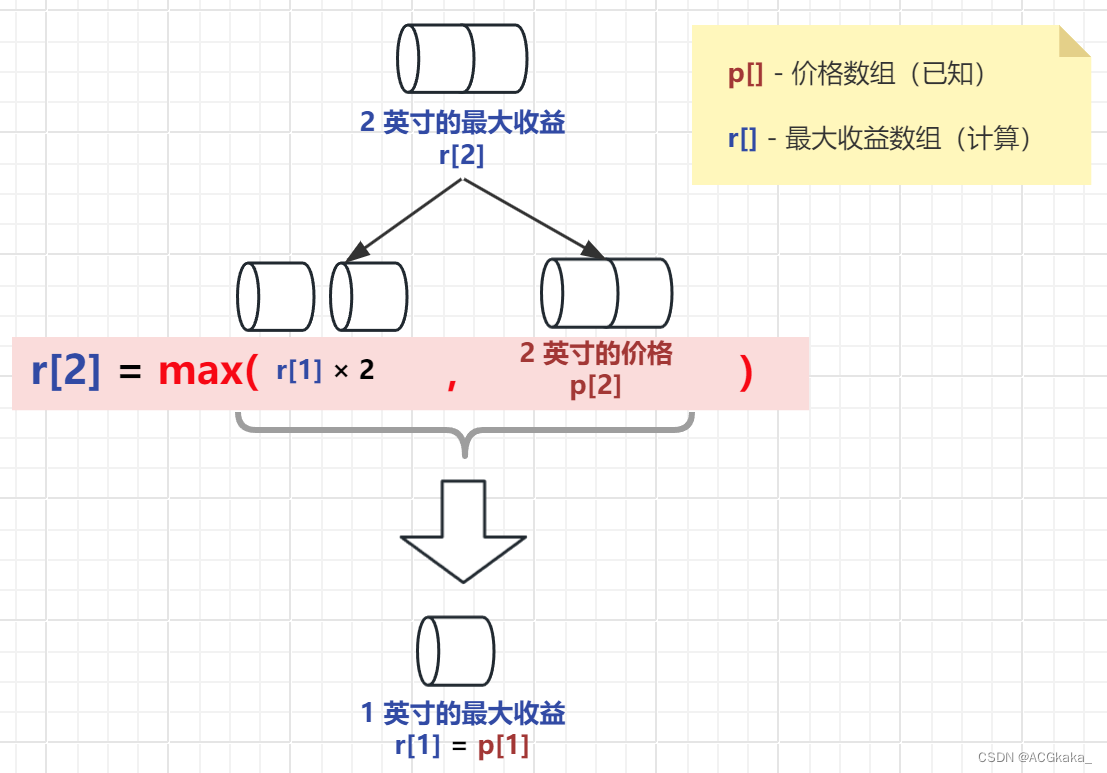
数据结构与算法(二)动态规划(Java)
目录 一、简介1.1 什么是动态规划?1.2 动态规划的两种形式1)自顶向下的备忘录法(记忆化搜索法)2)自底向上的动态规划3)两种方法对比 1.3 动态规划的 3 大步骤 二、小试牛刀:钢条切割2.1 题目描述…...

颜值实力“C位出道”:起亚EV6综合实力究竟怎么样?
作为起亚电动化转型的标杆之作,起亚EV6已在全球赢得广泛赞誉,连续斩获“2022欧洲年度汽车”及“2023北美年度汽车”等多项国际大奖,其GT版本更是荣获“2023年度世界性能车”,这些荣誉不仅标志着其设计和技术的国际认可,…...

继承和多态_Java零基础手把手保姆级教程(超详细)
文章目录 Java零基础手把手保姆级教程_继承和多态(超详细)1. 继承1.1 继承的实现(掌握)1.2 继承的好处和弊端(理解) 2. 继承中的成员访问特点2.1 继承中变量的访问特点(掌握)2.2 sup…...

AI:85-基于深度学习的自然场景生成与渲染
🚀 本文选自专栏:人工智能领域200例教程专栏 从基础到实践,深入学习。无论你是初学者还是经验丰富的老手,对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带有在本地跑过的代码,详细讲解供大家学习,希望可以帮到大家。欢迎订阅支持,正在不断更新中,…...

Windows电脑训练 RT-DETR 改进算法 (Ultralytics) 教程,改进RTDETR算法(包括使用训练、验证、推理教程)
手把手从零开始训练 RT-DETR 改进项目 (Ultralytics版本) 教程,改进RTDETR算法 本文以Windows服务器为例:从零开始使用Windows训练 RT-DETR 算法项目 《芒果剑指 RT-DETR 目标检测算法 改进》 适用于芒果专栏改进RT-DETR算法 文章目录 百度 RT-DETR 算法介绍改进网络代码汇…...
flask框架报错解决方法
1、报错 jinja2.exceptions.TemplateNotFound 解决方法:报错jinja2.exceptions.TemplateNotFound,template没找到,由于我之前直接将.html文件和.py文件直接放在同一目录下,经了解,需要新增一个 templates目录ÿ…...
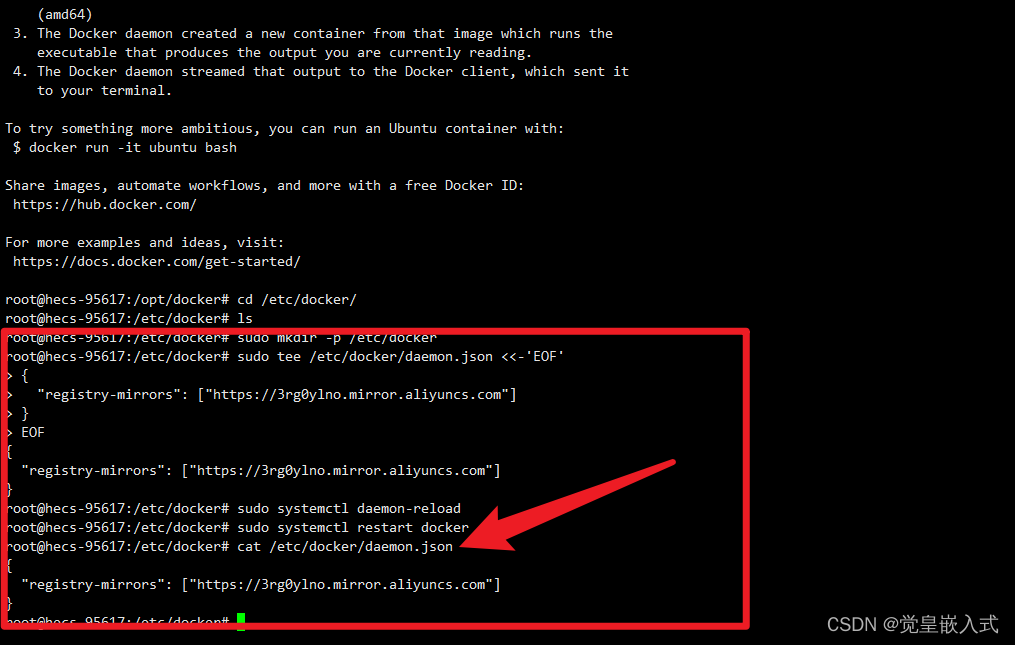
Ubuntu18.04 安装docker教程
Ubuntu18.04 安装docker教程 1、前言 Docker Engine-Community 支持以下的 Ubuntu 版本: Xenial 16.04 (LTS)Bionic 18.04 (LTS)Cosmic 18.10Disco 19.04 Docker Engine-Community 支持以下CPU架构: x86_64(或 amd64)armhfarm…...

深入理解Git
目录 一、Git 的基本构造 1.1 关键对象类型 1.2 存储机制 二、Git 的内部工作 2.1 哈希和数据完整性 2.2 引用和可达性 2.3 分支和合并 2.4 垃圾回收 三、Git 高级特性 3.1 垃圾回收 3.2 钩子(Hooks) 3.3 子模块 四、常用命令 五、最佳实践…...
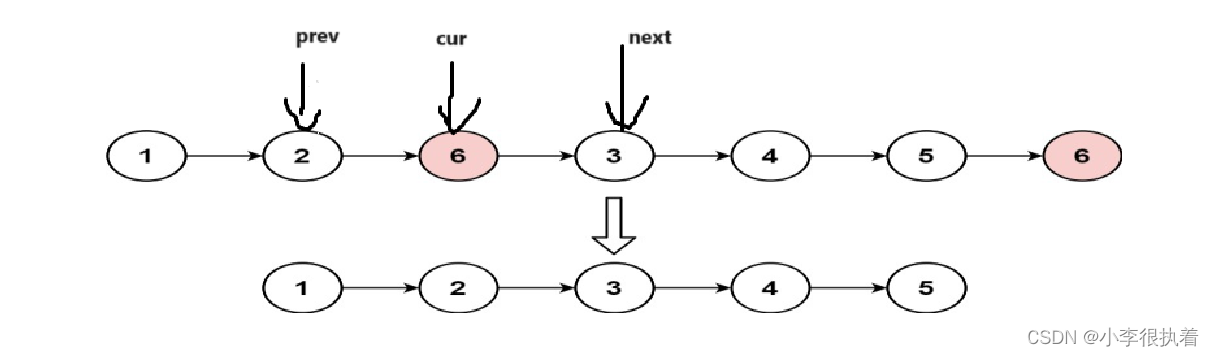
Leetcode_203.移除链表元素—C语言
目录 ❣️1.题目❣️ ❣️2.解答❣️ 💞方法一:暴力法 💞方法二: 尾插法 💞方法三:哨兵位法 ❣️1.题目❣️ 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.va…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
