深入理解Git
目录
一、Git 的基本构造
1.1 关键对象类型
1.2 存储机制
二、Git 的内部工作
2.1 哈希和数据完整性
2.2 引用和可达性
2.3 分支和合并
2.4 垃圾回收
三、Git 高级特性
3.1 垃圾回收
3.2 钩子(Hooks)
3.3 子模块
四、常用命令
五、最佳实践
Git,作为当代软件开发中最受欢迎的版本控制系统,其强大功能背后是一套复杂而精妙的存储原理和内部机制。理解这些原理不仅能帮助开发者更有效地使用 Git,还能提升对整个软件开发流程的理解。本文将深入探讨 Git 的存储原理和内部机制,揭示它如何管理和维护代码历史。
一、Git 的基本构造
Git 的设计哲学是以快照的形式存储数据,而非文件差异比较。每次提交时,Git 实际上是在创建项目状态的快照。这一点与其他版本控制系统存在根本区别。
1.1 关键对象类型
在 Git 中,数据存储和管理依赖于四种主要的对象类型:
-
Blob(二进制大对象):每个文件的内容存储在一个 blob 对象中。重要的是,blob 对象只包含文件数据,不包含任何文件名或目录结构信息。
-
Tree:tree 对象代表目录结构。它可以指向一组 blob 对象(文件)和其他 tree 对象(子目录),从而形成项目的层次结构。
-
Commit:commit 对象包含指向特定 tree 对象的指针(代表项目在某一时刻的快照),以及该提交的元数据,如作者、日期、父提交等。
-
Tag:tag 对象用于标记特定的提交(例如,作为版本发布点),提供了一种固定引用到特定提交的方法。
1.2 存储机制
Git 使用内容寻址文件系统,这意味着文件和目录的存储基于它们内容的哈希值。具体来说,Git 对每个文件内容计算 SHA-1 哈希值,并以此作为 blob 对象的唯一标识。这种方法不仅确保了数据的一致性和完整性,还允许 Git 高效地重用相同内容的文件,节约存储空间。
二、Git 的内部工作
理解 Git 如何在内部处理数据对于高效使用它至关重要。
2.1 哈希和数据完整性
Git 依赖于 SHA-1 哈希来保证数据完整性。每个对象(不论是 blob、tree 还是 commit)都有一个与其内容对应的唯一哈希值。任何内容的微小更改都会导致哈希值发生变化,从而提供一种自然的数据完整性检查机制。
2.2 引用和可达性
Git 中的“引用”(例如分支和标签)指向特定的提交。一个对象(提交、树、blob)的“可达性”是通过引用和提交历史来确定的。只要从任何现存引用出发,通过递归的父提交关系能够找到某个对象,就认为这个对象是“可达的”。不可达的对象(例如,通过 git reset 丢弃的提交)可能会在垃圾回收过程中被删除。
2.3 分支和合并
在 Git 中,分支本质上是指向特定提交的轻量级指针。创建新分支时,Git 只是创建了一个新的指针,而不会复制任何实际的文件数据。合并操作通常涉及到比较两个分支的差异,并生成一个新的合并提交。
2.4 垃圾回收
随着时间的推移,Git 仓库中可能会积累大量不再需要的对象。Git 的垃圾回收机制负责清理这些不再需要的对象,优化仓库的性能。
三、Git 高级特性
3.1 垃圾回收
随着时间的推移,Git 仓库会积累不再需要的对象。Git 的垃圾回收机制能够清理这些对象,优化仓库性能。
3.2 钩子(Hooks)
Git 钩子是自动化脚本,它们在执行重要 Git 操作(如提交、推送)时触发。钩子可用于代码审查、自动部署等任务。
3.3 子模块
Git 子模块允许将一个 Git 仓库作为另一个仓库的子目录。这对于管理依赖关系和大型项目非常有用。
四、常用命令
-
配置用户信息
git config --global user.name "Your Name" git config --global user.email "your_email@example.com" -
初始化仓库
git init # 在当前目录初始化新的Git仓库 -
克隆仓库
git clone <repository_url> # 克隆远程仓库 -
添加文件到暂存区
git add <file> # 添加指定文件 git add . # 添加当前目录的所有更改 -
提交更改
git commit -m "Commit message" # 提交暂存区的更改 -
查看状态
git status # 查看工作目录和暂存区状态 -
查看提交历史
git log # 查看提交历史 -
创建分支
git branch <branch_name> # 创建新分支 -
切换分支
git checkout <branch_name> # 切换到指定分支 git checkout -b <new_branch> # 创建并切换到新分支 -
合并分支
git merge <branch_name> # 将指定分支合并到当前分支 -
推送到远程仓库
git push origin <branch_name> # 推送当前分支到远程仓库 -
拉取远程仓库的更改
git pull # 拉取并合并远程仓库的更改
五、最佳实践
有效使用 Git 的关键在于遵循一些最佳实践:
- 频繁提交:经常提交可以帮助您保持工作进度的记录。
- 清晰的提交信息:编写清晰、具体的提交信息。
- 合理使用分支:为新功能或修复创建新的分支。
- 定期拉取和推送:保持与远程仓库的同步。
- 使用 .gitignore:排除不需要版本控制的文件。
- 避免重写公共历史:不在公共分支上使用
git rebase或git push --force。
相关文章:

深入理解Git
目录 一、Git 的基本构造 1.1 关键对象类型 1.2 存储机制 二、Git 的内部工作 2.1 哈希和数据完整性 2.2 引用和可达性 2.3 分支和合并 2.4 垃圾回收 三、Git 高级特性 3.1 垃圾回收 3.2 钩子(Hooks) 3.3 子模块 四、常用命令 五、最佳实践…...
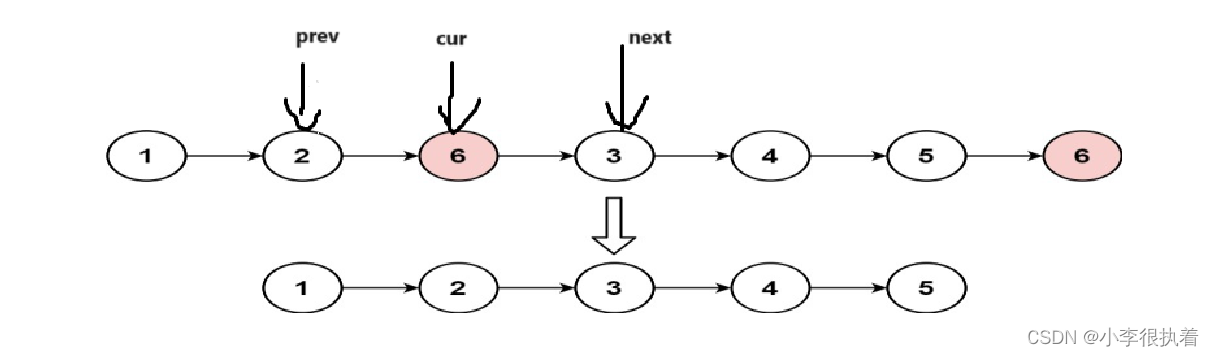
Leetcode_203.移除链表元素—C语言
目录 ❣️1.题目❣️ ❣️2.解答❣️ 💞方法一:暴力法 💞方法二: 尾插法 💞方法三:哨兵位法 ❣️1.题目❣️ 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.va…...
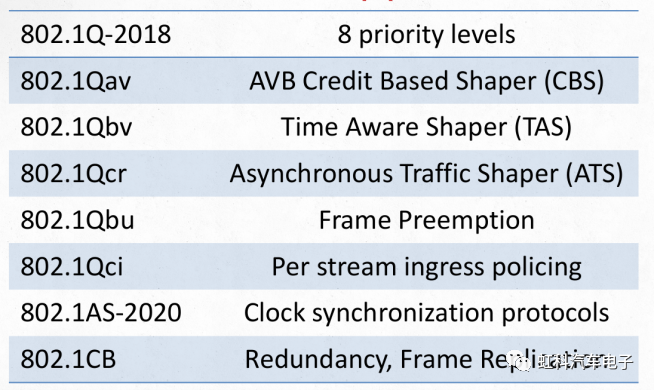
虹科方案 | 汽车电子电气架构设计仿真解决方案
来源:虹科汽车电子 虹科方案 | 汽车电子电气架构设计仿真解决方案 导读 本文将介绍面向服务(SOA)的汽车TSN网络架构,并探讨RTaW-Pegase仿真与设计软件在TSN网络设计中的应用。通过RTaW将设计问题分解,我们可以更好地理…...

Java6种单例模式写法
单例模式 某个类任何情况下只有一个实例,并提供一个全局访问点来获取该实例。Java6种单例模式:2种懒汉式,2种饿汉式 ,静态内部类 ,枚举类懒汉式 synchronized延迟加载 public class Singleton {private static Sing…...
Direct3D拾取
假设在屏幕上单击,击中的位置为点s(x,y)。由图可以看出,用户选中了茶壶。但是仅给出点s,应用程序还无法立即判断出茶壶是否被选中。所以针对这类问题,我们需要采用一项称为“拾 取(Picking)”的技术。 茶壶和屏幕点s之间的一种联…...

大洋钻探系列之二IODP 342航次是干什么的?(上)
本文简单介绍一下大洋钻探IODP 342航次,从中,我们一窥大洋钻探航次的风采。 IODP342的航次报告在网络上可以下载,英文名字叫《Integrated Ocean Drilling ProgramExpedition 342 Preliminary Report》,航次研究的主要内容是纽芬兰…...
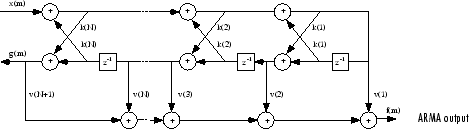
离散时间系统模型
离散时间系统模型 离散时间系统模型是表示数字滤波器的方案。MATLAB 科学计算环境支持若干种离散时间系统模型,这些模型将在以下章节中介绍: 传递函数零极点增益状态空间部分分式展开式(残差形式)二阶节 (SOS)格型结构体卷积矩…...
Nginx学习(在 Docker 中使用 Nginx)
1. 安装Nginx 使用 docker pull nginx 下载最新的 Nginx Docker 镜像。 下载完毕后,使用 docker run -d -p 80:80 --name nginx nginx,即可启动 Nginx 容器。其中,-p 80:80 表示将容器的 80 端口映射到 主机的 80 端口;--name ng…...
【Java】集合(一)单列集合List
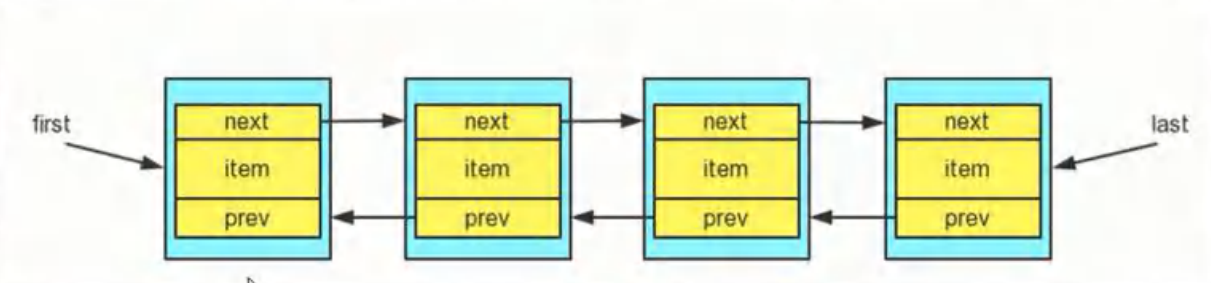
1.集合 可以动态保存任意多个对象,并提供了一系列的操作对象的方法:add、remove、set、get等。 2.集合框架体系 分为两大类: 单列集合和双列集合 3.List接口基本介绍 List接口是Collection接口的子接口 List集合类中元素有序࿰…...

实战 | 基于卷积神经网络的蘑菇识别微信小程序
一个不知名大学生,江湖人称菜狗 original author: Jacky Li Email : 3435673055qq.com Time of completion:2023.11.13 Last edited: 2023.11.13 导读:其实没啥难的,主要是随手搞了就发出来把,太久没有水过帖子了&…...

如何选择共享wifi项目服务商,需要注意哪些?
在移动互联网时代,无线网络已经成为人们生活中不可或缺的一部分。随着5G时代的到来,共享WiFi项目成为了市场上备受关注的焦点。在众多共享WiFi公司中,如何选择共享wifi项目服务商合作,今天我们就来盘点下哪些公司可靠!…...

ubuntu20.04 MYNTEYE S 相机运行与标定记录
ubuntu20.04 MYNTEYE S 相机运行与标定记录 环境 ubuntu20.04 opencv3.3.1 硬件 mynteye S1030 OpenCV 3.4.3 安装 Jetson Nano小觅相机(MYNT EYE S)开发调试指南 mkdir -p ~/tools/opencv cd ~/tools/opencvgit clone https://github.com/opencv/opencv.git cd opencv/…...
有效降低数据库存储成本方案与实践 | 京东云技术团队
背景 随着平台的不断壮大,业务的不断发展,后端系统的数据量、存储所使用的硬件成本也逐年递增。从发展的眼光看,业务与系统要想健康的发展,成本增加的问题必须重视起来。目前业界普遍认同开源节流大方向,很多企业部门…...
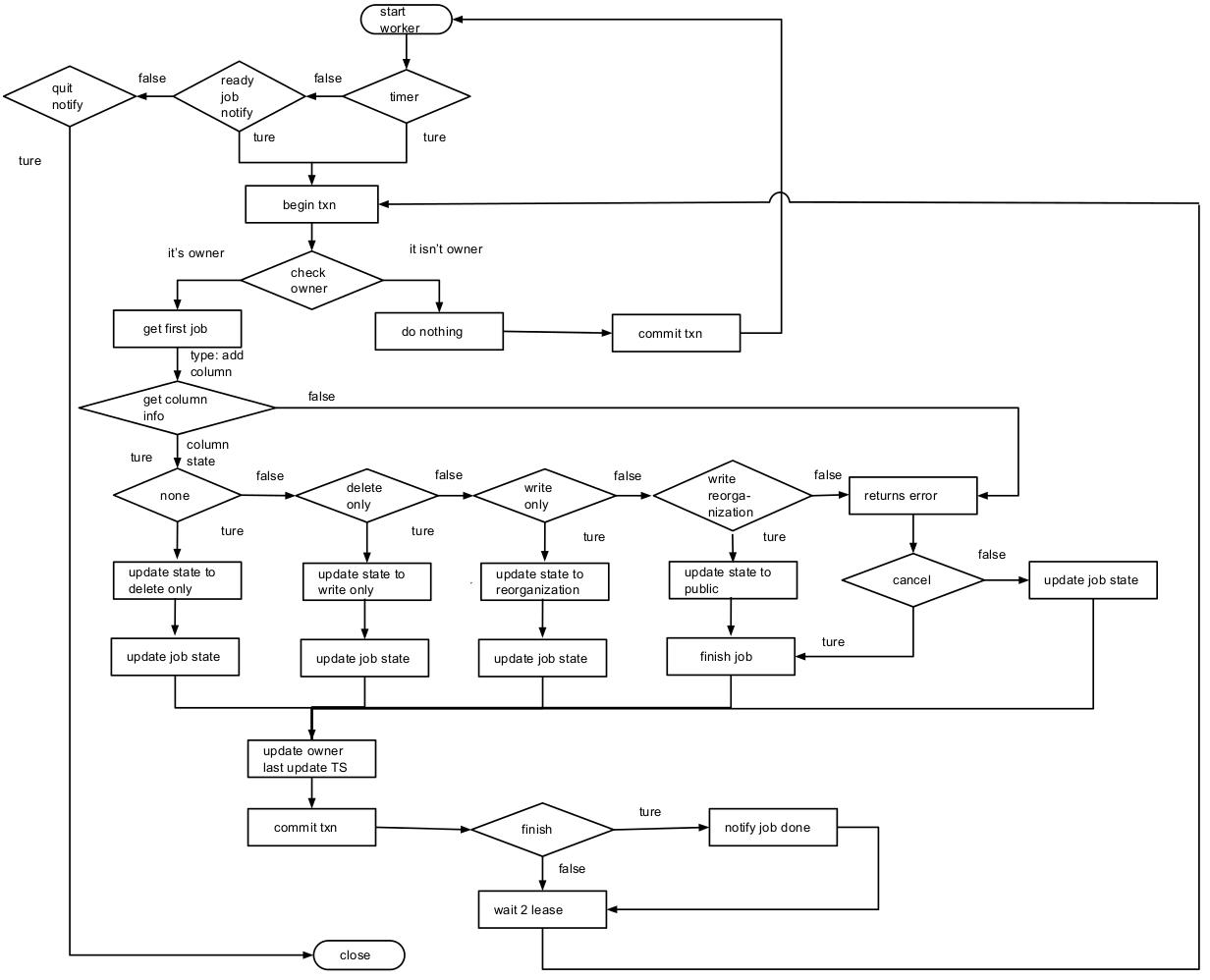
分布式数据库Schema 变更 in F1 TiDB
分布式数据库Schema 变更 in F1 & TiDB 【转载】TiDB 源码阅读系列文章(十七)DDL 源码解析 | PingCAP 上述文章主要叙述了从DDL语句发起到执行的过程,简单介绍了弄一套相同的模式来后台处理数据回填,从而提高DDL的并发度的一…...

图形库篇 | EasyX | 图像处理
图形库篇 | EasyX | 图像处理 图像类型 IMAGE表示图像,用于定义一个图像变量,与导入的图片资源一一对应。 IMAGE img;加载与绘制图像 函数功能函数加载图像void loadimage(IMAGE* pDstImg,LPCTSTR pImgFile,int nwidth = 0,int nHeight = 0,bool bResize = false)绘制图像v…...

AWTK UI 自动化测试工具发布
AWTK UI 自动化 提供了兼容 Appium 的接口,可以使用 Appium 的工具来进行 UI 自动化测试。但是使用起来有点麻烦,用的人不多,所以最终决定开发一个 AWTK 专用的 UI 自动化测试工具。相比 Appium,这个工具有下列特点: …...
Java后端开发——JDBC入门实验
JDBC(Java Database Connectivity)是Java编程语言中用于与数据库建立连接并进行数据库操作的API(应用程序编程接口)。JDBC允许开发人员连接到数据库,执行各种操作(如插入、更新、删除和查询数据)…...

LCA
定义 最近公共祖先简称 LCA(Lowest Common Ancestor)。两个节点的最近公共祖先,就是这两个点的公共祖先里面,离根最远的那个。 性质 如果 不为 的祖先并且 不为 的祖先,那么 分别处于 的两棵不同子树中&#…...

ts学习02-数据类型
新建index.html <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title> </h…...

javaSE的发展历史以及openjdk和oracleJdk
1 JavaSE 的发展历史 1.1 Java 语言的介绍 SUN 公司在 1991 年成立了一个称为绿色计划(Green Project)的项目,由 James Gosling(高斯林)博士领导,绿色计划的目的是开发一种能够在各种消费性电子产品&…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
